Investigando a relação entre pães mofados e função exponencial
Daniela Mendes Vieira da Silva
Seeduc-RJ
Introdução
Este trabalho apresenta a vivência de uma sequência pedagógica para o aprendizado de funções exponenciais planejada a partir da Taxonomia de Bloom revisada, fundamentada no aprendizado significativo de David Ausubel e na dedução informal de Mathias, sequência implementada em três momentos distintos. Primeira etapa: exposição de exemplos cotidianos, com ênfase para um exemplo particular: o crescimento de uma colônia de fungos em pães de forma. A utilização desse caso específico serviu como gatilho disparador da discussão da temática e da construção da generalização do assunto abordado. Segunda etapa: práticas laboratoriais com materiais concretos visando compreender o comportamento de algumas funções exponenciais tomadas uma a uma como exemplos específicos, e, portanto, definições informais do tema, além de um jogo educacional com o mesmo objetivo, sendo este acrescido da natural ludicidade que a competição propicia. Terceira etapa: modelagem matemática do crescimento da colônia supracitada. Em cada uma dessas vivências, os alunos foram estimulados a alcançar raciocínios cada vez mais complexos até atingir a etapa mais alta de cognição segundo a referida taxonomia, o sexto degrau, nomeado avaliação, em que eles puderam formalizar as funções exponenciais. Essa atividade foi vivenciada em uma escola estadual do Rio de Janeiro com resultados muito satisfatórios, comprovados por avaliações internas e externas, além de ter apresentado baixíssimo custo de implantação, podendo ser replicada com muita facilidade por outros docentes.
No Projeto Laboratório Sustentável de Matemática (LSM), desenvolvido e sediado no Colégio Estadual Hebe Camargo, estou sempre buscando abordagens pedagógicas significativas que facilitem o aprendizado dos alunos. Nesta busca surgiu um desafio: criar uma abordagem pedagógica que os auxiliasse a compreender o tema Função Exponencial, bastante abstrato.
Buscando solucionar essa problemática, encontrei na Taxonomia de Bloom (2001) o referencial teórico que nortearia a sequência pedagógica que seria nosso guia para que alcançássemos o objetivo. Segundo essa abordagem pedagógica, o aprendizado se dá em níveis cognitivos que crescem em complexidade, iniciando no conhecimento (nível 1) e alcançando a criação (nível 6), sendo este último degrau o mais elevado de todos, como está no Quadro 1.
Quadro 1: Estruturação da Taxonomia de Bloom no domínio cognitivo
| Conhecimento (palavra-chave: lembrar): Diz respeito ao aprendiz trazer à consciência informações e conteúdos já armazenados. |
| Compreensão (palavra-chave: entender): Relaciona-se à capacidade de o aprendiz entender o significado de uma informação ou de um fato. |
| Aplicação (palavra-chave: aplicar): Envolve a habilidade de o aprendiz usar informações em uma situação nova. |
| Análise (palavra-chave: analisar) Envolve a habilidade de o aprendiz separar as partes relevantes e irrelevantes e inter-relacioná-las. |
| Avaliação (palavra-chave: avaliar): Diz repeito ao aprendiz julgar a relevância e a organização de um dado material. |
| Criação (palavra-chave: criar): Relaciona-se à capacidade de o aprendiz juntar os elementos apreendidos em busca de uma nova ideia. |
Fonte: Bridon & Neitzel (2014).
Preparei a sequência pedagógica tendo esses degraus cognitivos como norteadores das práticas. A experiência é finalista do prêmio de educação científica B. G. Brasil 2015.
Desenvolvimento das atividades/experiências
Do conhecimento à compreensão
Segundo a taxonomia consultada, no primeiro degrau (conhecimento) é esperado do aprendiz que se lembre/memorize o que lhe for apresentado. Esse degrau se apresentou como um bom ponto de partida para nossas práticas; essa constatação se apoiou em David Ausubel, em que encontrei o esclarecimento de que o aluno só aprende a partir do que já sabe; portanto, para o sucesso dessa abordagem pedagógica seria essencial que o trabalho se iniciasse pela ancoragem dos conhecimentos que deveriam ser aprofundados pela apresentação deles aos estudantes em uma perspectiva memorativa. Isso não deve ser confundido com “educação bancária”, árida, mecânica, descontextualizada, tão duramente combatida pelo mestre Paulo Freire (2011). Meu objetivo aqui foi preparar terreno para a escalada dos demais degraus cognitivos, buscando o desenvolvimento do educando caminhando na direção oposta da educação mecânica, que inicia e termina nesse patamar cognitivo – o mais baixo de toda a escala. Partimos de exemplos particulares lembrados pelos alunos, como o crescimento do número de carros nas ruas; para tanto, escolhemos uma cidade fictícia fundada no ano 2000 que possui uma taxa de crescimento imaginária em que o número de carros nas ruas triplica a cada ano e montamos a seguinte tabela:
Tabela 1: Crescimento do número de carros em cidade imaginária
| Anos decorridos | Número de carros a cada ano | Quantidade de carros |
| 2000 = 0 | 5.000 | 5.000 |
| 2001 = 1 | 5.000 x 3 | 15.000 |
| 2002 = 2 | 5.000 x 3 x 3 | 45.000 |
| 2003 = 3 | 5.000 x 3 x 3 x 3 | 135.000 |
Fonte: Acervo pessoal.
A partir da análise de tabelas como a descrita acima para este e outros exemplos trazidos pelos alunos, chegamos à ideia e à generalização da função exponencial: y = ax; assim, chegamos ao segundo degrau (compreensão), em que se espera do educando que ele dê sentido ao conteúdo.
Visando levar nossos alunos a consolidar esse degrau, preparei uma oficina em que eles trabalharam, divididos em grupos, a generalização alcançada anteriormente; para tanto, utilizamos jogos e materiais concretos como subsídio.
A primeira parte da oficina foi vivenciada com o Jogo da Estrela, adaptado do jogo elaborado pelo GEMat-UERJ/Lúdica, em que os alunos receberam 4 estrelas como as mostradas a seguir com um número qualquer representado em seu centro.

Figura 1: Jogo da estrela
Fonte: Acervo pessoal.
O objetivo do jogo foi completar as pétalas de cada estrela escrevendo nelas 5 representações diferentes em forma de potência, calculadas com estratégias diferentes para cada pétala. Essa atividade propiciou uma revisão desse fundamento essencial à compreensão do tema função exponencial a ser trabalhado. Para vivenciá-lo, distribuí duas folhas, totalizando quatro estrelas desenhadas, cada uma com um número diferente em seu centro, e com as pontas em branco para cada grupo. A equipe vencedora foi aquela que completou suas quatro estrelas primeiro, de acordo com as regras.
Após o jogo, iniciei o segundo momento da nossa oficina: trabalhar com material concreto para explorar as funções exponenciais. Para tanto, inicialmente, as equipes receberam uma série de funções exponenciais para que descobrissem suas leis de formação.
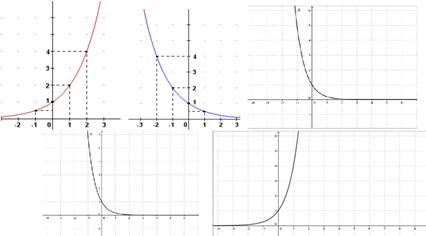
Figura 2: Funções recebidas pelos alunos
Fonte: Acervo pessoal.
Na sequência, os grupos receberam as funções exponenciais: f(x) = 3x, f(x) = (1/3)x, f(x) = 3-x, f(x) = (1/3)-x e f(x) = (1)x, além de um plano cartesiano milimetrado feito com sucata, onde eles construíram e analisaram em conjunto as funções recebidas de forma concreta.

Figura 3: Alunos analisando as funções recebidas com o apoio do plano cartesiano milimetrado
Fonte: Acervo pessoal.
Após a vivência com o material concreto, chegou o terceiro momento da atividade do dia, que buscou consolidar o aprendizado de todos os envolvidos. Nesse momento, os alunos foram convidados a montar quatro pirâmides planificadas (jogo adaptado a partir do Jogo da Estrela); na base de cada um estava grafada uma função exponencial, e cada lado da respectiva pirâmide deveria corresponder à função em sua base.

Figura 4: Pirâmide montada corretamente, com lados relacionados à sua base
Fonte: Acervo pessoal.
Neste jogo, que encerrou a oficina, assim como no que a abriu, venceu a equipe que montou suas figuras primeiro.
Nesta atividade foi fácil perceber que os alunos haviam construído o aprendizado, pois completaram a atividade muito rapidamente e com muita satisfação, mostrando que esta foi uma atividade agradável e instrutiva para todos.
Da aplicação à avaliação
No experimento que fechou a sequência pedagógica aqui apresentada, experimento este baseado nas pesquisas sobre modelagem matemática de Maria Salete Bienbegut (1999), que afirma que a modelagem matemática procura traduzir de forma simplificada um determinado fenômeno da realidade com o objetivo de compreendê-lo, galgamos os 3º, 4º e 5º degraus: Aplicação, no qual se espera que o educando utilize os conceitos compreendidos em situações novas; Análise, em que ele deve comparar, medir, contrastar o conhecimento construído; e Avaliação, em que ele pode julgar com conhecimento de causa o que aprendeu.
Aplicação
Levei para a sala de aula a proposta de acompanhar o crescimento de uma colônia de fungos (Aspergillus s.p.), o bolor de pão. Microrganismo que se desenvolve bem em temperatura ambiente, para o sucesso do experimento é imprescindível que ele aconteça em uma época quente do ano, em ambiente não refrigerado e que os pães sejam mantidos úmidos; esta atividade ocorreu em cinco dias corridos (para a realização desta investigação, contamos com a colaboração dos professores da escola para liberar a aluna Lorena sempre às 11h, para que ela acompanhasse o experimento).
Iniciamos o experimento em uma sexta-feira às 11h, data que foi marcada como dia 0. Convidamos uma aluna a contaminar uma fatia nova de pão de forma com bolor encontrado em um pacote de pão de forma velho. A área inicialmente infectada foi de 1cm² (área calculada de forma aproximada, considerando as manchas de crescimento das colônias como retângulos).

Figura 5: Momento da contaminação
Fonte: Acervo pessoal.
Nos dias seguintes (exceto sábado e domingo, pois não há aulas nesses dias), a aluna Lorena, no horário determinado (11h), umedeceu os pães, fotografou e anotou o crescimento da colônia.

Figura 6: Aparência da colônia de fungos na segunda-feira, dia 3 do experimento. Contaminação aproximada de 6cm²
Fonte: Acervo pessoal

Figura 7: Aparência da colônia de fungos na terça-feira, dia 4 do experimento. Contaminação aproximada de 18cm²
Fonte: Acervo pessoal.

Figura 8: Aparência da colônia de fungos na quarta-feira, dia 5 do experimento. Contaminação aproximada de 38cm²
Fonte: Acervo pessoal.
Análise
Com os dados reunidos pela aluna, na aula seguinte, ao fim do experimento, montamos a seguinte tabela:
Tabela 2: Dados coletados
| Dia | Contaminação |
| 0 | 1cm² |
| 1 | Sábado (não houve registro) |
| 2 | Domingo (não houve registro) |
| 3 | 6cm² |
| 4 | 18cm² |
| 5 | 38cm² |
Fonte: Acervo pessoal.
A partir dessas informações, marcamos os pontos no plano cartesiano concreto disponível no LSM. Os pontos A, B, C, D representavam os dados coletados a cada dia, estando nas abscissas o dia como variável independente (x) e nas ordenadas a área contaminada como variável dependente (y).
Assim, obtivemos: A = (0,1); B = (3,6); C = (4, 18); D = (5,38). Ao unirmos esses pontos com barbante, obtivemos um gráfico compatível com uma função exponencial. Na sequência, substituímos um dos pares ordenados (x, y) observados acima (o par C), na lei geral y = ax (trabalhada anteriormente), e calculamos o valor de “a”, obtendo uma lei de formação para esta função y = 2,06x.
Avaliação
Com os dados reunidos e a lei de formação da função determinada, foi o momento de analisar o crescimento da colônia estudada com o programa GeoGebra, a fim de comparar os dados obtidos com a lei de formação encontrada.
 Figura 9: Plano cartesiano milimetrado
Figura 9: Plano cartesiano milimetrado
Fonte: Acervo pessoal.
Para tanto, marcamos esses pontos no programa GeoGebra (programa que possibilita o desenho de pontos, vetores, segmentos, linhas e funções e a alteração dinâmica deles; auxilia no trabalho de Aritmética, Álgebra, Geometria e Cálculo). Como o programa não aceita números decimais no campo de entrada, inserimos a fração decimal y = (206/100)x.
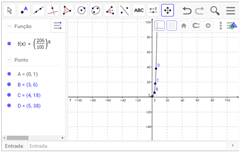
Figura 10: Tela do programa GeoGebra
Fonte: Acervo pessoal.
Observamos que os pontos A, C e D coincidiram com a função plotada e o ponto B ficou um pouquinho distante dela, o que é perfeitamente normal, pois, como se trata de Matemática Experimental, uma pequena margem de erro é esperada; mesmo assim, o valor encontrado se mostrou próximo da realidade do crescimento do microrganismo assexuado com o qual trabalhamos (um organismo assexuado se reproduz pela duplicação, em um processo chamado meiose), cuja reprodução pode ser apresentada como y = 2x.
Criação
O sexto degrau (criação) foi alcançado quando o aluno participante desta sequência pôde, a partir dela, julgar toda a atividade feita e criar novos experimentos – o que de fato ocorreu, pois ao findarmos a investigação os alunos conseguiram transpor o conceito para outras situações cotidianas, como o crescimento do montante de lixo em aterros sanitários, o crescimento exponencial da população humana, o crescimento de dívidas calculadas em juros compostos e que tais, apresentando uma visão amadurecida de todo o processo vivido.
Reflexões
A Taxonomia de Bloom revisada se mostrou um excelente recurso pedagógico. Com seu apoio foi possível planejar e executar uma sequência pedagógica que levou os alunos ao mais alto patamar de desenvolvimento cognitivo. Esse desenvolvimento foi sentido pelo excelente desempenho nas avaliações qualitativas e quantitativas das quais esses alunos participaram no bimestre de realização da sequência pedagógica.
Referências
AUSUBEL, D. P. A aprendizagem significativa: a teoria de David Ausubel. São Paulo: Moraes, 1982.
BIEMBENGUT, Maria Salett. Modelagem Matemática & Implicações no Ensino-Aprendizagem de Matemática. Blumenau: Editora FURB, 1999.
BELHOT, R. V.; FERRAZ, A. P. C. M. Taxonomia de Bloom: revisão teórica e apresentação das adequações do instrumento para definição de objetivos instrucionais. Disponível em http://www.scielo.br/scielo.php?pid=S0104-530X2010000200015&script=sci_arttext. Acesso em 21 mar. 2015.
BRIDON, Janete; NEITZEL, Adair de Aguiar. Competências leitoras no Saeb: qualidade da leitura na educação básica. Educ. Real., Porto Alegre, v. 39, nº 2, p. 437-462, jun. 2014. Disponível em: http://www.scielo.br/scielo.php?script=sci_arttext&pid=S2175-62362014000200006&lng=en&nrm=iso. Acesso em 30 maio 2015. http://dx.doi.org/10.1590/S2175-62362014000200006.
FREIRE, Paulo. Pedagogia da autonomia: saberes necessários à prática educativa. 43ª ed. São Paulo: Paz e Terra, 2011.
______. Pedagogia do oprimido. 12ª ed. Rio de Janeiro: Paz e Terra, 1983.
MATHIAS, C. E. M. Informática no ensino da Matemática: repensando práticas. Volume 5. UFF/UAB/MEC, 2008. Disponível em www.lanteuff.org/moodle. Acesso em 24 jun. 2015.
SILVA. D. M. V. Matemática é ciência. Revista do professor, Belo Horizonte, nº 120, 2014.
Meus agradecimentos especiais ao meu grupo de pesquisa GEMAT-UERJ, especialmente à minha coordenadora Gabriela Brião, aos meus companheiros de pesquisa Barbara Marinho, Darling Domingos, Bruno Penedo, Karina Costa, Vinícius Borovoy e Nazareno Passos e ao meu colega de trabalho, o professor de biologia Anderson Dias Cezar, que atuou como consultor do experimento com o bolor de pão.
Publicado em 07 de junho de 2016
Como citar este artigo (ABNT)
. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/16/12/investigando-a-relacao-entre-paes-mofados-e-funcao-exponencial
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

