O uso de tecnologias no ensino do Teorema de Pitágoras
Rafael Camargo Cardoso
Introdução
Nas últimas décadas, o ensino da Matemática vem sofrendo fortes influências de uma sociedade que, com o passar do tempo, apresenta características cada vez mais particulares. Com a evolução tecnológica, o ensino da Matemática também sofreu mudanças em sua aplicabilidade, visto que hoje os métodos não são os mesmos de décadas atrás. O grande desafio enfrentado pelos docentes com essas fortes transformações é saber como inserir as novas tecnologias nas práticas diárias, visto que sua formação profissional foi diferente, ou seja, tradicional.
Seria um delírio pretender mudar completamente o método atual de ensino da Matemática nas escolas, ou seja, substituir de imediato a metodologia tradicional por novas tecnologias de ensino. A razão disso é que a metodologia tradicional está na base da formação dos professores, e a mudança dessa metodologia só poderá ser alcançada de forma gradativa (Júnior, 2002).
Ainda segundo Júnior (2002), o objetivo não é substituir de maneira cabal e imediata a metodologia tradicional, o que não parece razoável, mas introduzir novos procedimentos tecnológicos educacionais para melhorar o ensino da Matemática.
Segundo Simon (2013), a formação do professor deve ser de extrema importância para o estudo das diferentes abordagens das teorias do desenvolvimento para que o processo de ensino-aprendizagem venha a responder às necessidades do aluno.
A principal consciência que se deve ter quanto a inserir a tecnologia no ensino da Matemática é que não apenas aparelhos eletrônicos e materiais de últimas gerações são exemplos de tecnologia em sala de aula; muitas vezes pequenos materiais como régua, compasso, materiais manipulativos podem ser de grande contribuição para o processo de ensino-aprendizagem da disciplina.
O presente trabalho tem por objetivo apresentar o conteúdo matemático Teorema de Pitágoras de forma tecnológica, utilizando como ferramentas básicas o software R.E.C e materiais manipulativos confeccionados pelos próprios discentes, a fim de perceber que uma mesma atividade proposta apresenta diversas formas de ser resolvida, estimulando o senso crítico e a capacidade de interpretação do que está sendo proposto.
Este trabalho tem como principais características uma pesquisa exploratória, pois, segundo Gil (2008), apresenta uma abordagem direta do conteúdo – Teorema de Pitágoras – a partir de uma pesquisa de campo, buscando compreender como a tecnologia está sendo inserida em sala de aula e se ela é eficaz para o processo de ensino-aprendizagem, utilizando para o seu desenvolvimento o método indutivo; segundo Pereira e Filho (2007), esse método parte da experiência de casos particulares para a generalização ou universalização, ou seja, as conclusões são mais abrangentes que as premissas.
A pesquisa utiliza tecnologias como o software Régua e Compasso e materiais manipulativos. O desenvolvimento dele fez-se necessário a partir da percepção dos autores, em diferentes momentos de suas vidas profissionais, da grande dificuldade enfrentada pelos discentes para interpretar e desenvolver atividades propostas utilizando o que lhes foi apresentado, porém empregando suas próprias percepções.
Pressupostos teóricos
Abordagem histórica
Pitágoras foi um grande estudioso de sua época; nasceu na ilha de Samos, nas costas da Ásia Menor, por volta do ano 572 a.C. (Amaral, 2008). Nessa época, Samos era uma rica cidade-estado mercantil, mas, talvez justamente por isso, sua vida intelectual era muito limitada, apesar de viverem ali muitos homens de talento. Esse fato, aliado ao duro regime político sob o qual Samos vivia, deve ter sido o motivo que levou Pitágoras, que sempre revelara pendores místicos e filosóficos, a deixar a cidade.
“O menino, mesmo quando criança, é diferente dos demais; seu rosto é sereno, corpo saudável, chora somente o necessário, muito cedo ele aprendeu a andar e falar” (Conte, 2006).
Com 18 anos de idade, Pitágoras já conhecia e dominava muitos conhecimentos matemáticos e filosóficos da época. Por meio de estudos astronômicos, afirmava que o planeta Terra era esférico e suspenso no espaço (ideia pouco conhecida na época). Encontrou certa ordem no universo, observando que as estrelas, assim como a Terra, giravam ao redor do sol.
Segundo Amaral (2008), Pitágoras, seguindo conselho de pessoas pelas quais tinha grande admiração, foi residir em Mileto, onde encontrou Tales. A partir dessa viagem, Pitágoras passou a conhecer diferentes países, culturas, ajudando também a lapidar sua personalidade, aumentar seus conhecimentos; Tales ensinou a Pitágoras que uma nova visão do mundo deveria ter sempre uma base racional, capaz de progredir, evoluir, ser repensada e substituída, quando assim o determinassem a evidência e a experiência.
Os espaços já estavam ficando pequenos para Pitágoras; ele se destacava em todos onde estivesse. Ele foi para o Egito e lá foi admitido nos graus iniciativos de Isis e Osíris; durante muitos séculos, ele foi o único estrangeiro a graduar-se nos Mistérios Sagrados. De iniciado passou a iniciador, de discípulo a mestre, de sacerdote passou a hierofante; com isso ele aprendeu muito, mas também ensinou.
Segundo Conte (2008), a volta de Pitágoras em Samos durou pouco tempo; com isso ele foi para Crotona, no sul da Itália, onde descobriu que lá existiam as melhores escolas de Medicina da Grécia e que lá era um centro de culto a Orpheu e Apolo, cuja filosofia sempre foi apreciada por Pitágoras. “Jamais um pitagórico o chamou pelo nome e sim por “Mestre” e, depois de morto, como Divino Mestre” (Conte, 2008).
Em Crotona, Pitágoras fundou uma escola que, apesar de seu misticismo, iria ter influência muito grande nos rumos da Filosofia e da Ciência, especialmente da Matemática. Pitágoras é considerado o pai da Matemática e da Música, e um dos mais importantes filósofos daquela época, como afirma o filósofo Bertrand Russel, que classificou Pitágoras como “um dos homens mais importantes de todos os tempos no plano intelectual” (Amaral, 2008).
Segundo Aristóteles, o Mestre Sâmio era capaz de estar em dois lugares ao mesmo tempo. Um exemplo disso foi quando ele estava em Mesaponto, na Itália, visitando alguns amigos, e ao mesmo tempo estava em Touromênio, na Sicília, fazendo um discurso com duas profecias. Uma delas falava que a Escola de Crotona seria incendiada, saqueada e destruída; a segunda afirmava que ela renasceria das cinzas. As duas profecias se cumpriam anos mais tarde.
Pitágoras pode ser considerado um dos principais teóricos matemáticos até a atualidade; mas ele não se restringia aos estudos matemáticos, entendia de tudo um pouco e contribuiu de forma significativa para diversas áreas do conhecimento.
O nome de Pitágoras está associado a um importante teorema que tem como base o triângulo retângulo; na época, este foi um grande marco, pois apresentou uma nova forma de demonstração matemática. O teorema desenvolveu-se enquanto Pitágoras fazia mais uma de suas visitas a diversas cidades e dessa vez ficou impressionado com as grandes pirâmides do Egito, onde elaborou o famoso Teorema de Pitágoras. Ao desenvolver o teorema, provou que é possível calcular o lado de qualquer triângulo retângulo conhecendo apenas os outros dois. O Teorema de Pitágoras é provavelmente o mais célebre dos teoremas da Matemática; estabelece uma relação simples entre o comprimento dos lados de um triângulo retângulo.
Segundo Figueiró et al.(2012), o mais famoso tablete de argila encontrado na Babilônia, contém sequências de números correspondentes às “ternas pitagóricas” – denominado Plimpton 322 –; foi utilizado entre 1900 e 1600 a.C. Porém o que se pode perceber, a partir de nossas observações durante os estágios ainda na graduação, é que muitas discentes não conhecem os verdadeiros fatos e apenas apresentam o que lhes é descrito nos livros didáticos.
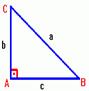
O famoso teorema descreve a relação entre a soma dos quadrados dos catetos e o quadrado da hipotenusa em um triângulo retângulo: “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. Geometricamente, pode-se representar essa relação conforme a Figura 1.
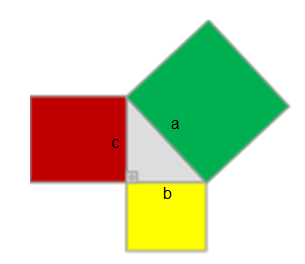
Figura 1 - Quadrado dos lados do triângulo
Com base na Figura 1, podemos escrever:
a² = b² + c²
Abordagem do Teorema de Pitágoras nos livros didáticos
Os livros didáticos podem ser considerados grande ferramenta utilizada em salas de aulas, auxiliam satisfatoriamente no processo de ensino-aprendizagem, por apresentar muitas vezes contextos claros e fazer uma conexão com o que está sendo dito. Segundo Vercez e Silvino (2008), o livro didático, na perspectiva bakhtiniana, pode ser visto como um enunciado que constitui um elo na cadeia de comunicação verbal, estabelecida por professores e alunos na sala de aula. Desse modo, na interação face a face, constitui um mecanismo relevante para os processos de leitura e compreensão de textos. Se o professor souber explorá-lo, fazendo uso de sua criatividade, inserindo, com textos, a diversidade de gêneros textuais necessária ao alunado, certamente lhe propiciará boas reflexões sobre sua realidade.
Em muitos livros, o Teorema de Pitágoras é abordado com uma breve fundamentação teórica e a tradicional forma de demonstrá-lo, a partir da comparação das áreas. Pesquisou-se a abordagem desse teorema em três livros, que comentamos a seguir.
Gelson Iezzi, Osvaldo Dolve e Antonio Machado (2005), ao editarem o livro Matemática e Realidade - 8ª serie do Ensino Fundamental, apresentam uma introdução histórica sobre o assunto, relatando um pouco sobre vida, obra e importância do Teorema de Pitágoras, e demonstram o teorema de acordo com a demonstração 2 e 3 descrita no decorrer do trabalho e acreditam na tese de que “a demonstração dada por Pitágoras deve ter sido uma demonstração geométrica, baseada na comparação de áreas”.
Segundo Iezzi et al. (2005), a suposta demonstração de Pitágoras é desconhecida, mas se acredita que tenha sido feita por comparação de áreas, como a que apresentaremos a seguir, ilustrada pela Figura 2.
Do quadrado maior (de lado a + b) da figura da direita, retiramos os quatro triângulos retângulos congruentes de catetos a e b. O que resta é um quadrado de lado c. Do quadrado da figura da esquerda, retiramos também os quatros triângulos retângulos de catetos a e b. Restam dois quadrados de áreas a² e b². Como as figuras resultantes das retiradas dos triângulos têm mesma área, então:
a² + b² = c²
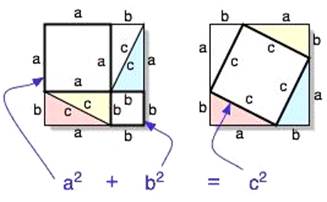
Figura 2 – Ilustração de uma demonstração prática do Teorema de Pitágoras
Centenas de demonstrações diferentes desse importante teorema já foram feitas depois de Pitágoras. O livro The Pythagoream Proposition (O teorema de Pitágoras), de E. S. Loomis (1852-1942), em edição de 1940, traz cerca de 360 dessas demonstrações (Iezzi et al., 2005).
A obra Praticando Matemática, de Álvaro Andrini e Maria José Vasconcellos, para o 9º ano, anos de 2004, 2005 e 2006, publicado pela Editora do Brasil, faz uma breve abordagem histórica e apresenta a demonstração de Pitágoras por comparações de áreas e por relação entre as medidas dos lados de um triângulo retângulo. A partir de um triângulo retângulo, são construídos quadrados com as mesmas medidas referentes aos lados do triângulo. Observa-se que a soma dos quadrados construídos sobre os outros dois é igual à área do quadrado construído sobre o maior lado do quadrado, como mostra a Figura 3.
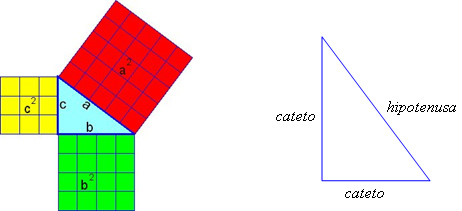
Figura 3 – Forma tradicional do Teorema de Pitágoras
Segundo Edwaldo Bianchini, no livro para o 9º ano (2011, 2012 e 2013), publicado pela Editora Moderna, o Teorema de Pitágoras é abordado com uma parte histórica mais detalhada e desenvolve o teorema somente a partir das equivalências de áreas, como já desenvolvido pelos autores anteriores.
Diante das propostas disponibilizadas nos livros didáticos, apesar de o Teorema de Pitágoras ter muitas demonstrações, as mais utilizadas pelos autores são as mesmas, diferindo somente na abordagem histórica, em que uns trazem mais detalhes.
É relevante pensar no fato de que, para que o livro didático seja um instrumento facilitador em sala de aula, o professor precisa, além de conhecer a ideia do autor em questão, lançar mão de estratégias em que o conteúdo a ser ofertado pelo livro didático seja trabalhado de maneira qualitativa e dinamizada. Selecionar a obra é apenas o início; adaptar o conteúdo para a turma e para a aula é um desafio para o educador. O professor é um facilitador indispensável na construção do conhecimento.
Materiais manipulativos
Os materiais manipulativos são importantes recursos didáticos que contribuem de forma significativa para o processo de ensino-aprendizagem. A aplicação desses materiais em aulas de Matemática consegue fazer uma ligação da teoria com a prática. Essas estratégias são bastante presentes até o final do 1º segmento do Ensino Fundamental; se bem planejadas, podem tornar as aulas mais atrativas e dinâmicas, aproximando cada vez mais os discentes dos docentes.
Materiais manipuláveis são objetos desenvolvidos e/ou criados para trabalhar com conceitos matemáticos de forma que venham a facilitar a compreensão e o desenvolvimento do aluno, de modo que os estudos possam ser realizados de maneira prazerosa. Salientamos que, na maioria das vezes, esses materiais são produzidos pelos próprios alunos (orientados pelo professor), o que aumenta a quantidade de conteúdos que podem ser trabalhados. Também podem ser confeccionados pelo professor somente (Souza; Oliveira, 2010).
Segundo Rodrigues e Gazire (2012), os materiais didáticos em uma aula de Matemática, na maioria das vezes, têm objetivo funcional, uma vez que são utilizados como suporte experimental na organização do processo de ensino-aprendizagem. Entretanto, a autora considera que o verdadeiro objetivo desse material didático é servir de mediador na construção do conhecimento, “facilitando a relação professor/aluno/conhecimento”.
O planejamento das atividades, assim como a atuação do docente na aplicação das atividades, é determinante para o sucesso, pois com seu papel de mediador do conhecimento é que irá se tornar o diferencial para a eficácia da estratégia. Segundo Barroso e Franco (2010), não se constrói um conhecimento simplesmente tocando, observando ou manipulando objetos. Para Piaget, o conhecimento se dá a partir da organização, da estruturação e da explicação do experienciado.
Utilização de software em sala de aula
Com os avanços tecnológicos, a necessidade de se adaptar e inserir novos métodos de ensino se fez necessária na hora de lecionar. Hoje, a principal desvantagem do uso de meios tecnológicos no processo de ensino-aprendizagem é a falta de capacitação de docentes. Segundo os Parâmetros Curriculares Nacionais, “entre os obstáculos que o Brasil tem enfrentado em relação ao ensino de Matemática, aponta-se a falta de uma formação profissional qualificada, as restrições ligadas às condições de trabalho, a ausência e as políticas educacionais efetivas e as interpretações equivocadas de concepções pedagógicas” (Brasil, 1998, p. 21).
A utilização de mídias e tecnologias atua de forma significativa no ensino-aprendizagem da Matemática. Promover propostas de atividades para o ensino do Teorema de Pitágoras utilizando materiais lúdicos e tecnológicos diminuiu a distância que a Matemática tem na vida escolar dos alunos. Dessa forma, desenvolver trabalhos em que seja possível atrair os alunos ao conteúdo e assim desenvolver uma aprendizagem satisfatória é um dos principais desafios educacionais da atualidade. Trabalhar com o Teorema de Pitágoras é um caminho relevante e possível mediador para alcançar com excelência os objetivos estabelecidos.
O desenvolvimento de competências e habilidades ligadas à tecnologia é um fator muito importante na globalização, já que hoje os alunos vivem em uma conexão direta com o mundo virtual. O professor é visto como facilitador no processo de ensino-aprendizagem e, por esse motivo, disponibilizar ao educando a utilização de tecnologias, com a participação direta dele desafia-o a ter uma aprendizagem qualitativa; tais instrumentos são facilitadores quando utilizados de maneira adequada pelo educador, levando-o a promover novas habilidades para então atuar como mediador na construção do conhecimento, se tornando de fato um profissional do século XXI.
Software Régua e Compasso
O programa Régua e Compasso (R. e C.) foi desenvolvido pelo professor René Grothmann, da Universidade Católica de Berlim, na Alemanha. Trata-se de um software de Geometria Dinâmica Plana, escrito na linguagem Java, com código aberto, e que roda em qualquer plataforma, como Windows, Linux, Macintosh, Solaris etc. (Martins; Fioreze, 2008).
A cada minuto percebemos que a tecnologia ganha um espaço transformador na educação brasileira. O uso de ferramentas tecnológicas, como os softwares no Ensino da Matemática, consegue transcrever para os discentes de forma clara o que lhes é dito ou até mesmo como preencher lacunas apresentadas pelos livros didáticos. Silva (2011) diz que os PCN citam que “as imagens, por si mesmas, permitem compreensão ou demonstração de uma relação, regularidade ou propriedade”, como é o caso da representação do Teorema de Pitágoras, através de figuras geométricas.
Um dos grandes diferenciais desse software é sua utilização em escolas públicas, visto que possui licença gratuita e compatível com os sistemas operacionais mais utilizados. Disponibilizar para o estudante o direito da descoberta de um teorema tão importante como esse com o auxílio de tal ferramenta é estar atualizado, buscando vencer os obstáculos encontrados nas aulas de Matemática. A utilização desse software disponibiliza uma aprendizagem conceitual desenvolvida diretamente pelos alunos, já que ele possui manuseio fácil, prático, em que a aprendizagem vai além da coparticipação dos discentes.
Resultados e discussões
Para a realização deste trabalho, foi aplicada uma aula prática em uma turma do 9º ano do Ensino Fundamental regular de um colégio estadual da cidade de Valença/RJ, a fim de comprovar as percepções de que o uso da tecnologia é um grande recurso para o processo de ensino-aprendizagem. Inicialmente foi feita uma pequena pesquisa com alunos, em que foram questionadas as maiores dificuldades em desenvolver estudos na área da Matemática. Pode-se observar o resultado na Tabela 1.
Tabela 1 - Pesquisa de campo
| Descrição |
Porcentagem |
|
Interpretação |
40% |
|
Resolução |
24% |
|
Falta de conhecimento do conteúdo |
13% |
|
Defasagem das séries anteriores |
18% |
|
Outros |
5% |
Com base na pesquisa e seguindo a linha de objetivos traçados previamente, pode-se comprovar que a maioria dos discentes apresenta maior dificuldade em interpretar os problemas matemáticos, entender o que lhes é proposto, o que dificulta e desestimula todo o processo de ensino-aprendizagem. A partir das análises iniciais, buscaram-se estratégias que pudessem facilitar e estimular as aulas de Matemática e seu aprendizado. Um dos principais desafios dos docentes atualmente é conseguir atrair a atenção dos discentes utilizando apenas materiais como giz e quadro, entre outros, enquanto eles utilizam instrumentos cada vez mais atuais, como celulares de última geração e tablets em sala de aula. Houve então a necessidade de inserir instrumentos que visassem prender a atenção dos discentes e ao mesmo tempo estimular o aprendizado. Piaget afirma que o aprendizado depende da interação do indivíduo com o meio; isso pode ser notado perfeitamente quando inserimos a tecnologia em sala de aula.
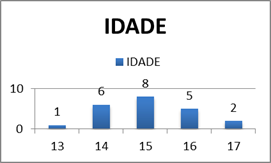
A turma à qual foi aplicada a aula prática para a realização deste trabalho estava composta de 22 alunos, apresentando idades bastante variadas, conforme o Gráfico 1, o que pode ser um desafio ainda maior, pois se sabe que cada faixa etária apresenta comportamentos e estímulos diferenciados.
Gráfico 1 – Demonstrativo das idades da turma
A aula prática foi dividida em 4 partes:
- 1ª parte: Histórica;
- 2ª parte: Introdução ao triângulo retângulo;
- 3ª parte: Estudo do teorema de forma tecnológica e atrativa;
- 4ª parte: Aplicação do estudo.
Para introduzir esse tema descreveu-se a parte histórica, apresentando vida e obra de Pitágoras, abordada em uma linha do tempo, a fim de mostrar passo a passo a evolução dele até chegarmos à criação de seu teorema, com intuito de compreender todo o conceito da sua criação e sua fundamentação.
Em um segundo momento da aula, foi proposto revisar as principais características do triangulo retângulo para facilitar o entendimento posterior do Teorema de Pitágoras. Inicialmente foi definido que essa figura “é um triângulo que possui um ângulo reto, isto é, um dos seus ângulos mede 90º, daí o nome triângulo retângulo. Sabemos que a soma das medidas dos ângulos internos de um triângulo é igual a 180°, então podemos dizer que a soma dos outros dois ângulos será de 90°”. Definiram-se também as nomenclaturas dos segmentos laterais do triângulo, como pode ser observado na Tabela 2.
Tabela 2 – Nomenclaturas do triangulo retângulo
|
Letra |
Lado |
Triângulo |
Vértice = Ângulo |
Medida |
|
A |
Hipotenusa |
|
A = Ângulo reto |
A = 90° |
|
B |
Cateto |
B = Ângulo agudo |
B < 90° |
|
|
C |
Cateto |
C = Ângulo agudo |
C < 90° |
Em seguida foi apresentado o enunciado do famoso Teorema de Pitágoras: “O quadrado da hipotenusa é igual à soma dos quadrados dos catetos”.
Na primeira atividade motivadora sobre o assunto, foi proposto que os discentes desenhassem e recortassem um triângulo conforme apresenta a Figura 4, com as seguintes medidas: 3 centímetros, 4 centímetros e 5 centímetros; em seguida pediu-se que construíssem quadrados com as mesmas medidas dos lados do triângulo e unissem os quadrados menores (de lados 3 e 4) sobrepondo ao quadrado maior (de lado 5); conseguiu-se então comprovar o teorema. O que mais chamou a atenção dos alunos foi conseguir provar o teorema sem utilizar cálculos. Apesar de os alunos nunca terem ouvido falar do software R. e C., todas as atividades propostas foram desenvolvidos no aplicativo pelo docente, o que chamou ainda mais a atenção dos alunos, pois após a realização o software apresenta uma ferramenta que mostra todos os procedimentos realizados passo a passo, e os alunos observaram que tanto tecnologicamente quanto manualmente é possível demonstrar o teorema sem o apoio de um cálculo primário.

Figura 4 – 1º passo da demonstração tradicional

Figura 5 – 2º passo da demonstração tradicional

Figura 6 – 3º passo da demonstração tradicional.
Um dos principais objetivos dessa aula era mostrar para os discentes que um mesmo problema matemático apresenta diversas formas de ser interpretado e resolvido, e para tanto foi proposta outra demonstração para que eles pudessem perceber perfeitamente tais ideias. Essa demonstração é fundamentada por quatro triângulos retângulos semelhantes e que juntos conseguem, por movimentação deles, demonstrar, assim como o exemplo anterior, o Teorema de Pitágoras. A demonstração diz que dados quatro triângulos retângulos semelhantes (conforme a Figura 7), movimentando-os, pode-se determinar uma nova figura (Figura 8), e nessa figura é possível observar as seguintes características:
- 1 quadrado maior de lado b + c;
- 4 triângulos retângulos;
- 1 quadrado pequeno de lado a.
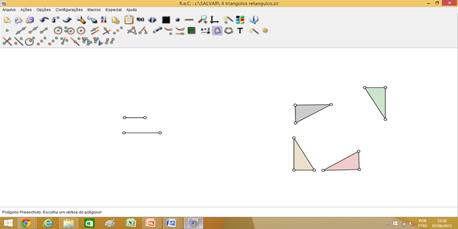
Figura 7 – Triângulos retângulos semelhantes
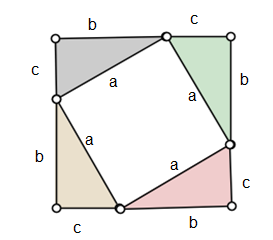
Figura 8 – Figura formada a partir dos triângulos retângulos
A partir das informações construídas, como mostram as Figuras 6, 7 e 8 desenvolvidas pelos próprios alunos, e da apreciação das mesmas construções propostas pelo docente no software R. e C., os alunos foram desafiados a demonstrar o teorema a partir das informações visuais que tinham em mãos. Nesse momento, foi realizado um trabalho percorrendo os grupos e fazendo questionamentos construtivos, a fim de auxiliá-los no desenvolvimento da atividade. Por fim após várias considerações positivas feitas pelos alunos, foi desenvolvida a demonstração a partir da afirmação de que a área do quadrado maior é igual à soma dos quatros triângulos retângulos mais o quadrado menor; algebricamente podemos transcrever da seguinte forma:
(b + c)² = 4 . ![]() + a²
+ a²
b² + 2 . b . c + c² = 2 . b . c + a²
Como nos dois lados da igualdade temos termos semelhantes, podemos simplificá-la; logo, teremos:
b² + 2 . b . c + c² = 2 . b . c + a²
a² = b² + c²
Portanto, conseguimos chegar à igualdade proposta por Pitágoras. A partir desse momento, foi mostrado aos discentes, com o auxilio da comparação dos exemplos feitos, que para um mesmo exercício temos diversas formas, instrumentos e meios de resolvê-lo.

Figura 9 - Construção dos retângulos

Figura 10 - Construção das diagonais dos retângulos para a construção dos quatro triângulos retângulos

Figura 11 - Desenvolvimento do teorema
Em seguida, para finalizar a parte inicial da aula, foi apresentada uma videoaula do Novo Telecurso, em que foi possível rever de forma resumida e com outras palavras tudo que tinha sido apresentado anteriormente, o que é de grande contribuição para o ensino, pois a parte visual é uma ferramenta indispensável para o processo de ensino-aprendizagem.
Para avaliar todo o aprendizado, foi proposta uma lista de exercícios em que os alunos tinham que inicialmente interpretar e, a partir daí, montar suas próprias estratégias para resolvê-los.
Num âmbito acadêmico, a aula foi bastante produtiva e de grande contribuição para o processo; na visão da professora da turma, a aula apresentou características inovadoras que conseguiram prender a atenção dos discentes e, de forma bastante dinâmica, atingir todos os objetivos propostos. Segundo os alunos, a aula nem parecia ser de Matemática; eles afirmaram que, se todas as aulas introduzissem a tecnologia, a Matemática seria uma disciplina bem melhor.
Conclusões finais
O Teorema de Pitágoras é apresentado como um dos mais importantes teoremas da Geometria Plana, pois apresenta características diferentes das outras demonstrações que eram feitas na época de sua descoberta. Por apresentar resoluções simples e de fácil entendimento, porém de grande significância, esse teorema ganhou grande importância no meio escolar. O Teorema de Pitágoras pode ser aplicado em diferentes áreas do conhecimento e de diferentes formas sem perder seus princípios.
Neste trabalho foram desenvolvidas etapas para ênfase do estudo do Teorema de Pitágoras utilizando modelos concretos construídos com material emborrachado (EVA) e papel, o software matemático Régua e Compasso, vídeos e a sua parte histórica dentro da Matemática visando construir o conhecimento de forma completa, desde a vida e obra de Pitágoras até as suas aplicações. Os modelos propostos podem ser considerados materiais didáticos que apresentam como principal objetivo facilitar a visualização e o entendimento das propriedades geométricas, a fim de facilitar o processo de ensino-aprendizagem.
O uso de ferramentas tecnológicas no processo escolar vem ganhando grande destaque com o passar dos anos. Pelo fato de serem instrumentos do cotidiano dos discentes, a tecnologia é uma ferramenta com a qual se pode garantir a eficiência e os objetivos propostos quando utilizada de maneira produtiva e construtiva. Assim entendemos que o ato de produzir e aplicar o Teorema de Pitágoras com o apoio tecnológico vai muito além do que nos é passado num ensino tradicional da Matemática. É preciso levar em consideração novos métodos para o aprimoramento e a aquisição do conhecimento matemático.
Pode-se concluir, com a aplicação deste trabalho, que o uso da tecnologia e dos materiais manipulativos foi de grande significância para o desenvolvimento e sucesso da aula. O ponto que se destacou no correr da aula foi a atenção e a concentração que os discentes tiveram em todos os momentos, além de estar sempre dispostos a desenvolver o que lhes foi proposto.
Foi possível perceber a grande contribuição das estratégias apresentadas, pois o desenvolvimento das atividades foi realizado de forma satisfatória, segundo a docente da turma, e percebeu-se a motivação e o entusiasmo para com os docentes no desenvolver delas. Alguns pontos de Matemática básica foram observados no decorrer da aula, o que fez perceber que esses são grandes empecilhos para melhor desenvolver as atividades, como por exemplo o uso de régua. Essa etapa da aula foi bastante lenta, porém produtiva, pois não foram desprezadas as dificuldades, que foram percebidas, levantadas e sanadas conforme o interesse dos discentes.
Muito ainda precisa ser feito para que a inserção da tecnologia em sala de aula seja feita de forma mais eficaz. Pode-se descrever como dois grandes vilões dessa metodologia a capacitação dos docentes e a estrutura organizacional da escola, porém é notório que já houve grande avanço nessa área.
Referências
ANDRINI, A.; VASCONCELLOS, M. Praticando Matemática. 9º ano. São Paulo: Editora do Brasil, 2006.
AMARAL, J. Teorema de Pitágoras. Monografia (Especialização). Universidade Federal de Minas Gerais, Belo Horizonte, 2008.
BARROSO, M.; FRANCO, V. O conhecimento de professores sobre laboratório de ensino da Matemática. X Encontro Nacional de Educação Matemática. Salvador/BA, 2010.
BIANCHINI, E. Matemática. 9º ano. São Paulo: Moderna, 2013.
BRASIL. Parâmetros Curriculares Nacionais. terceiro e quartos ciclos do Ensino Fundamental. Brasília, 1998. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/matematica.pdf. Acesso em 23 mar. 2015.
CONTE, C. Pitágoras: ciência e magia na Antiga Grécia. São Paulo: Madras, 2006.
EVANGELISTA, J. Teorema de Pitágoras: algumas extensões/generalizações e atividades com o software GeoGebra. Dissertação (Mestrado). Instituto de Biociências, Letras e Ciências Exatas da Universidade Estadual Paulista “Júlio de Mesquita Filho”, campus de São José do Rio Preto, 2014.
FIGUEIRÓ, L; VARGAS, D.; OLIVEIRA, E.; SANTOS, L.; COUTO, M. Atividades Diferenciadas no Ensino do Teorema de Pitágoras. Instituto Federal Farroupilha – Campus Júlio de Castilhos. Farroupilha, 2012.
GERTRUDES, M. Geometria plana com auxilio do software régua e compasso. Centro Universitário Franciscano. Santa Maria/RS, 2008.
GIL, A. Como elaborar projetos de pesquisa. 5ª ed. São Paulo: Atlas, 2008.
IEZZI, G.; DOLVE, O.; MACHADO, A. Matemática e Realidade. 8ª serie. São Paulo: Moderna, 2005.
JÚNIOR, A. Novas tecnologias educacionais no ensino de Matemática: Estudo de caso - Logo E do Cabri-Géométre. Dissertação (Mestrado). Universidade Federal de Santa Catarina Programa de Pós-graduação em Engenharia de Produção. Florianópolis, 2002.
MARTINS, L.; FIOREZE, L. O uso do software Régua e Compasso na construção de mosaicos. Disc. Scientia. Série. Ciências Naturais e Tecnologias, Santa Maria, v. 9, n.1, p. 143-162, 2008.
RIBEIRO, M. P. As inovadoras práticas na aplicação do Teorema de Pitágoras. Trabalho de Final de Curso de Pós-Graduação Lato Sensu de Novas Tecnologias no Ensino da Matemática (NTEM) do Lante, Universidade Federal Fluminense. Niterói, 2015.
PASSOS, C. L. B. Materiais manipuláveis como recursos didáticos na formação de professores de matemática. In: LORENZATO, Sérgio. Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006. p. 77-92.
PEREIRA, E. Sales. O método indutivo. Ver. Cient. Fac. Filho, v. 5, n. 1, 2007.
PERES, E. Martins Kruger. O ensino do Teorema de Pitágoras e as novas tecnologias. VI Congresso Nacional de Ensino da Matemática. Ulbra, Canoas/RS, 16,17 e 18 de outubro.
RIBEIRO, M. As inovadas práticas na aplicação do Teorema de Pitágoras. Trabalho de Final de Curso de Pós-Graduação Lato Sensu de Novas Tecnologias no Ensino da Matemática (NTEM) do Lante, Universidade Federal Fluminense. Niterói, 2015.
RODRIGUES, F.; GAZIRE, E. Reflexões sobre o uso de materiais didáticos manipulativos no ensino da Matemática: da ação experimental à reflexão. Revemat, Florianópolis, v. 7, n. 2, p. 187-196, 2012.
SCHMIDT, M. Gertrudes. Geometria Plana com o auxílio do software Régua e Compasso. Trabalho final de Graduação apresentado ao Curso de Matemática – Área de Ciências Naturais e Tecnológicas, do Centro Universitário Franciscano. Santa Rita, 2008.
SILVA,J. O software Régua e Compasso como recurso metodológico para o ensino da Geometria dinâmica. Mestrado em Ensino de Ciências e Matemática. Universidade Estadual da Paraíba. Campina Grande, 2011.
SOUZA, A.; MAGNAVITA, M.; BOTELHO, M.; MATOS, V.; OLIVEIRA, Z. Recursos e novas tecnologias no ensino de Matemática. Instituto Federal de Educação, Ciência e Tecnologia da Bahia. Eunápolis, 2010.
SOUZA, G.; OLIVEIRA, J. O uso de materiais manipulativos e jogos no ensino de Matemática. X Encontro Nacional de Educação Matemática. Salvador/BA, 2010.
TELECURSO. O Teorema de Pitágoras na Matemática. Ensino Fundamental, Aula 54. Disponível em: https://www.youtube.com/watch?v=Pxs0pnWLJu8. Acesso em 3 Jun. 2015.
VERCEZ, R.; Silvano, E. O livro didático e suas implicações nas escolas públicas de Guarajá-Mirim. Praxis Educacional, Vitória da Conquista, p. 83-102, 2008.
VERRI, I. O Teorema de Pitágoras. Dissertação (Mestrado). Pontifícia Universidade Católica de São Paulo, São Paulo, 2000.
Publicado em 08 de novembro de 2016
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.