A construção do conceito do Teorema de Tales utilizando o software Régua e Compasso

Viviane de Lima Noronha

Especialista em Novas Tecnologias no Ensino da Matemática (NTEM/Lante/UFF)

Introdução

Este trabalho tem como objetivo investigar o processo de ensino e aprendizagem do conceito do Teorema de Tales utilizando o software de Geometria dinâmica Régua e Compasso. Para tanto, foram realizadas atividades com alunos do Ensino Fundamental da rede pública do Estado do Rio de Janeiro. O trabalho descreve a metodologia utilizada em sala de aula com o uso do software; a aula consistiu na revisão de alguns conceitos de Geometria plana, como retas paralelas e transversais, segmentos de reta e as propriedades de razão e proporção, além de aplicação de um tutorial, realização de atividades e questionário. Esse software foi utilizado porque se acredita que esse recurso didático potencializa o ensino de Geometria plana, principalmente no que se refere ao conceito do Teorema de Tales, proporcionando aos alunos uma aprendizagem verdadeiramente significativa. Pelo desenvolvimento do presente estudo, foi possível observar que o uso das novas tecnologias em sala de aula dinamiza as aulas de Matemática, entretendo mais o alunado, e que o software em questão auxilia na compreensão do conteúdo abordado.

O presente trabalho foi implementado em turma de nono ano do Ensino Fundamental do Estado do Rio de Janeiro, pois foi observado nas aulas de Matemática que a maioria dos alunos apresentava muitas dificuldades para compreender os conceitos geométricos e, portanto, se sentiam desmotivados a aprender. Além disso, verificou-se também a falta de preparo de muitos docentes em tratar os conteúdos geométricos com os seus alunos.

O trabalho tem como objetivo geral investigar e identificar as vantagens da utilização do software de Geometria dinâmica Régua e Compasso no processo de ensino-aprendizagem do conceito de Teorema de Tales e como objetivos específicos revisar e reforçar os conceitos de retas paralelas e transversal, segmentos de reta e as propriedades razão e proporção; apresentar o software de Geometria dinâmica Régua e Compasso aos alunos; investigar e testar conjecturas sobre o conceito de Teorema de Tales; possibilitar a verificação do conceito do Teorema de Tales; estimular o aluno a construir e a desenvolver o conhecimento geométrico de maneira criativa, construtiva, dinâmica e interativa.

A teoria do trabalho foi desenvolvida baseando-se nas ideias de Veloso (1998) e Leite (2013), dentre outros, que abordam a importância do ensino e da aprendizagem da Geometria para alunos e professores; e em Mathias (2008), Fortes (2013) e Veleda (2014), que falam sobre os benefícios de utilizar os softwares de Geometria no ensino e aprendizagem de conceitos geométricos.

O conceito do Teorema de Tales foi adotado, primeiramente, por ser um assunto que aborda algumas propriedades fundamentais no estudo da Geometria plana e que muitos alunos desconhecem ou nas quais sentem dificuldades, razão e proporção, além dos problemas que as envolvem, e por ser pré-requisito de conteúdos como Semelhança de Figuras Planas - conceito da Geometria plana tratado no nono ano.

O software Régua e Compasso foi escolhido porque, segundo Fortes (2013), “os softwares educativos apresentam inúmeras capacidades funcionais e propriedades que podem ser reconhecidas e aproveitadas por professores e alunos, de modo a obter resultados eficientes no processo de ensino e aprendizagem de Matemática”. Essas capacidades e propriedades permitem, de acordo com Veleda (2014), “que os alunos façam aproximações, organizações e reorganizações de conceitos matemáticos”, podendo chegar à elaboração e verificação de conjecturas. Ainda sobre o software, Fortes (2013) conclui que “é de fácil manuseio e composto por uma interface bem apresentável e didática”. Além disso, o software permite a construção de figuras geométricas planas que podem ser alteradas pelas funções que compõem a sua barra de ferramentas. Tais alterações e construções exploram vários conceitos e assuntos relacionados à Geometria plana. Conforme Mathias (2008), “o recurso computacional é uma poderosa ferramenta para a criação de um ambiente de investigação geométrica”. Além das vantagens relacionadas ao conteúdo, esse software incentiva a criatividade e a descoberta.

Portanto, acredita-se que esse recurso auxilia na construção conceitual do Teorema de Tales por facilitar a sua visualização e possibilitar a elaboração e a demonstração desse teorema por meio da investigação, da verificação e da descoberta de uma maneira criativa.

Metodologia

O trabalho deteve-se a investigar, com a utilização do software Régua e Compasso, a construção conceitual do Teorema de Tales por alunos do nono ano do Ensino Fundamental em uma turma de uma escola pública estadual do Rio de Janeiro. Para tanto, primeiramente, foi apresentado aos alunos o software para depois ser abordada a teoria. A investigação realizou-se em duas aulas de dois tempos de 50 minutos cada e empregou projetor multimídia, notebook, quadro branco e questionário.

Na primeira aula foi feita uma revisão sobre retas paralela e transversal, segmentos de reta, razão e proporção. Em seguida, foi apresentado o software Régua e Compasso, realizado o tutorial e as atividades propostas com os alunos. Como a escola não possui sala de informática, as atividades foram realizadas em conjunto com o professor e com o auxílio do projetor multimídia. Elas objetivaram investigar o Teorema de Tales e o Princípio da Propriedade Mantida (PPM).

Na segunda aula, os alunos responderam a um questionário que constou de questões que foram resolvidas individualmente. Os resultados do questionário foram divulgados por meio de tabulação e gráfico de setores, com o intuito de avaliar a aprendizagem e a eficácia do método de ensino utilizado. Após o questionário foi apresentado o conceito do Teorema de Tales.

Resultados e discussões

A implementação do trabalho seguiu as seguintes etapas:

• Apresentação do software Régua e Compasso aos alunos (etapa 1);
• Revisão sobre retas paralelas e transversais, razão e proporção. Construção do feixe de retas paralelas cortado por duas transversais, por meio de um tutorial (etapa 2);
• Visualização do Teorema de Tales (teste do PPM com atividades propostas) (etapa 3);
• Questionário (individual) (etapa 4);
• Enunciado do Teorema (teoria) (etapa 5).

A primeira, a segunda e a terceira etapas foram aplicadas na primeira aula. A quarta e a quinta etapas foram trabalhadas na segunda aula. Essas aulas estão detalhadas a seguir:

Primeira aula

Apresentação, revisão e construção, visualização do Teorema de Tales

Etapa 1

Inicialmente foi apresentado aos alunos o software Régua e Compasso, para que houvesse familiarização com o recurso virtual. Em seguida, foram enfatizados os principais objetos que compõem a sua barra de ferramentas.

Etapa 2

Nessa etapa desejou-se que os alunos fossem capazes de construir o conceito do Teorema de Tales, partindo de feixes de retas paralelas cortados por duas transversais. Para tanto, foram revisados alguns elementos da Geometria plana, como retas paralela e transversal, e as propriedades de razão e proporção. Em seguida, no software Régua e Compasso e com o uso do projetor multimídia, foi realizada a construção dos feixes de retas paralelas cortados por duas transversais, seguindo o passo a passo do tutorial. A Figura 1 apresenta a construção realizada.

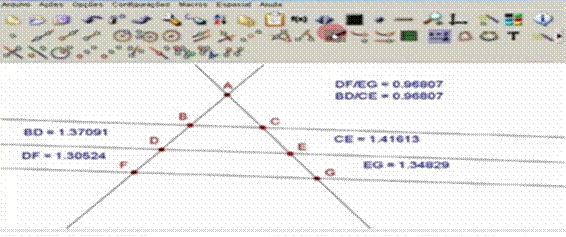
Figura 1: Construção dos feixes de paralelas e duas transversais no software Régua e Compasso

Etapa 3

Nessa etapa os alunos realizaram, juntamente com o professor e o auxílio do projetor multimídia, algumas atividades com o objetivo de testar o PPM e visualizar o Teorema de Tales.

Na Atividade 1, foi pedido que os alunos dessem valores para os segmentos 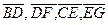 da Figura 1. Solicitou-se, em seguida, que os alunos comparassem os resultados encontrados para os quocientes  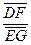  e  .

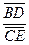Na Atividade 2, foi pedido que os alunos observassem o que acontecia com os valores dos quocientes encontrados ao mover, primeiramente, o ponto A.

Na Atividade 3, foi pedido que os alunos observassem também o que acontecia com os valores dos quocientes ao mover os pontos B, C, D, E, F e G.

Nas Atividades 4 e 5, foi pedido aos alunos que investigassem o que acontecia com os quocientes e a proporção ao movimentar os demais pontos. Por fim, foi solicitado que os alunos concluíssem o que haviam investigado, partindo do seguinte questionamento: “o que podemos concluir a respeito de retas paralelas interceptadas por retas transversais que se interceptam em um ponto?”.

Na primeira aula, observou-se que os alunos, mesmo sem nunca terem tido contato com algum recurso multimídia matemático, se adaptaram muito bem ao software, pois responderam às questões propostas sem maiores dificuldades. Também foi observado que o que mais chamou a atenção dos alunos com relação ao software foi a sua estrutura dinâmica e a sua praticidade.

É importante comentar também que, na Atividade 4, os alunos admitiram diversos valores para os quocientes 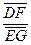 e 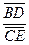, conforme sugere a atividade. E verificaram que, independentemente dos valores admitidos para os quocientes, haverá sempre uma proporção entre eles. Verificação do PPM. Isso pode ser constatado por meio de algumas das respostas dos alunos para essa atividade.

Segunda aula

Questionário e enunciado do Teorema de Tales

Etapa 4

Após a realização das atividades com o uso do software, os alunos responderam a um questionário que constou de duas questões. Nelas, os alunos testaram seus conhecimentos a respeito da construção e visualização do Teorema, de modo a avaliar a aprendizagem e a eficácia do método de ensino utilizado. Para a realização do questionário foi necessário papel quadriculado, lápis e régua.

Na primeira questão, foi solicitado que os alunos traçassem duas retas transversais e três retas paralelas interceptando-as. Em seguida, eles marcaram os pontos de interseção, dando nomes a esses pontos; mediram os segmentos que surgiram com a interseção e obtiveram o quociente desses segmentos. Em seguida, foi pedido que aumentassem o espaço entre as paralelas e refizessem os cálculos. Por fim, foi pedido que analisassem os resultados obtidos para as razões e as proporções.

Na segunda questão, foi pedido que os alunos traçassem duas transversais cortadas por três retas não paralelas. Em seguida, que medissem os segmentos construídos e calculassem os quocientes desses segmentos. Por fim, foi pedido que comparassem e analisassem os resultados dos quocientes obtidos. O principal questionamento foi se havia ou não uma proporção entre eles.

A primeira questão foi respondida pelos alunos sem muitas dificuldades. Na segunda questão, alguns alunos receberam auxílio com relação à construção das retas não paralelas. Eles questionaram como deveria ser a desenho dessas retas. Os alunos foram orientados com representações feitas no quadro. Depois de sanada a dúvida, em outro momento, os alunos perguntaram sobre os resultados diferentes que obtiveram para as proporções. Como resposta, foram remetidos às atividades que fizeram com o software; assim eles conseguiram fazer uma conexão entre o que haviam investigado e o que estavam analisando no questionário. Depois de esclarecidas as dúvidas, os alunos conseguiram realizar a tarefa sem mais dificuldades.

Acredita-se que os objetivos da pesquisa foram alcançados, pois as vantagens que o recurso pode oferecer puderem ser identificadas ao longo da realização das atividades e do questionário. Quanto a este, tabulando as respostas dos 45 alunos que participaram de sua realização, foi observado que:

Para a questão 1:

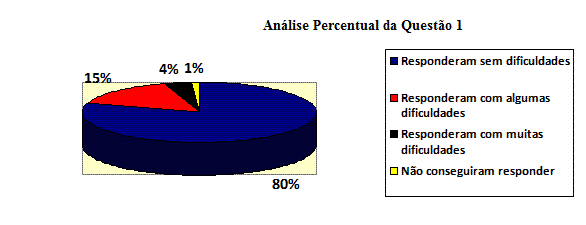
Figura 2: Resultados da Questão 1

Para a questão 2:

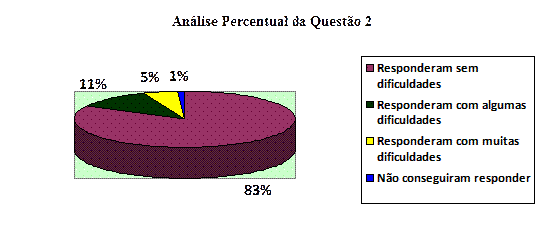
Figura 3: Resultados da Questão 2

Com esses resultados, pode-se observar que:

• Mais de 90% dos alunos conseguiram responder bem ao questionário.
• Mais de 95% dos alunos conseguiram transpor o conhecimento que foi construído com a ajuda do software para uma atividade que utiliza lápis e papel.
• O software Régua e Compasso auxiliou os alunos a compreender o assunto tratado.

Etapa 5

Após o questionário, foi enunciado no quadro o Teorema de Tales, partindo de um feixe de retas paralelas cortado por duas transversais, conforme Giovanni, Castrucci & Machado (2009). Nas discussões sobre o Teorema, observou-se que os alunos compreenderam que, se os segmentos não forem proporcionais, o Teorema não se valida; independente dos valores atribuídos aos segmentos, teremos sempre como resultado uma proporção entre as razões; trocando às retas paralelas por retas não paralelas, o Teorema também não é válido. Por fim, observou-se, por meio da investigação que ocorreu via software, que os alunos obtiveram êxito na construção do conhecimento, o que os auxiliou na compreensão das questões do questionário e, posteriormente, a entender o enunciado do Teorema.

Conclusões

A pesquisa revelou que a revisão de alguns conceitos que são pré-requisitos do Teorema, aliada à introdução dele por meio do software Régua e Compasso, proporcionou aos alunos uma aprendizagem que ocorreu pela observação, discussão e investigação, tornando as aulas mais atrativas e dinâmicas. A pesquisa também mostrou que muitos alunos sentem dificuldades com alguns conceitos e propriedades introdutórias do Teorema de Tales, tais como retas paralelas e transversais, segmento de reta, feixes de retas, razão e proporção. Porém as dificuldades foram sendo superadas a partir do momento em que foi introduzido o software, pois a ferramenta auxiliou na visualização das figuras construídas e nos cálculos que se sucederam, promovendo então a compreensão desses assuntos.

Referências

FORTES, P. R; PAZUCH, V. Explorando o software régua e compasso. 2013. Disponível em: http://www.pucrs.br/famat/viali/tic_literatura/artigos/pacotes/MC49.pdf. Acesso em: 10 mar. 2015.

GIOVANI J.; CASTRUCCI, B; MACHADO, A. A conquista da Matemática. 6º ano. São Paulo: FTD, 2009.

LEITE, R. S. O ensino de parte da Geometria do Ensino Fundamental: análise de dificuldades e sugestão de sequência didática. 2013. Disponível em: bit.profmatsbm.org.br/xmlui/bitstream/handle/123456789/475/2011_00367_RONDINELI_SCHULTHAIS_LEITE.pdf?sequence=1. Acesso em: 05 mar. 2015.

MATHIAS, C. E. A máquina, a matemática e o homem: interesses e possibilidades em diferentes universos. Rio de Janeiro: UFF, 2008.

VELEDA, G. G. O software Régua e Compasso para o ensino-aprendizagem de Geometria plana. 2014. Disponível em: http://sbemparana.com.br/arquivos/anais/epremxii/ARQUIVOS/MINICURSOS/autores/MCA014.pdf. Acesso em: 01 mar. 2015.

VELOSO, E. Geometria: temas actuais. Lisboa: IIE, 1998.