Diferentes significados da fração: um estudo diagnóstico com estudantes do curso de Pedagogia a distância
Alexandre Herculano Ferreira Freitas
Universidade do Estado do Rio de Janeiro
Gabriela dos Santos Barbosa
Universidade do Estado do Rio de Janeiro
Introdução
O presente artigo tem como objetivo apresentar os resultados parciais de uma pesquisa mais ampla que investiga as concepções dos estudantes de um curso de Pedagogia a distância em relação ao conceito de número racional em sua representação fracionária – fração. Mais especificamente apresentamos aqui as concepções dos estudantes quando começam a estudar os principais conceitos relacionados às frações e ao seu ensino na disciplina Matemática na Educação II do referido curso.
A coleta de dados se deu por meio de um fórum virtual. Os sujeitos da pesquisa mencionaram apenas os significados parte-todo, medida e quociente e sinalizaram a necessidade de atividades lúdicas e materiais manipulativos no ensino de fração. O fórum virtual se revelou não só um instrumento de pesquisa, mas um instrumento de aprendizagem colaborativa e construção de conhecimento.
A abordagem das frações tem início no 2º ciclo do Ensino Fundamental (mais precisamente no 4º ano) e deve criar condições para que os estudantes percebam que os números naturais não são suficientes para o domínio de todas as situações – entre elas podemos citar as situações que envolvem medições e divisões não exatas. O ensino de frações não pode ficar restrito à aplicação de um conjunto de técnicas que culminem na resolução de problemas. É preciso reconhecer que a aprendizagem de frações supõe algumas rupturas com as ideias já construídas pelos estudantes a respeito dos números naturais.
Os Parâmetros Curriculares Nacionais (PCN) (1998) sinalizam que, quando os estudantes dão às frações o mesmo tratamento que já davam aos números naturais, passam a enfrentar sérias dificuldades e cometem erros e equívocos. Segundo o documento, uma dificuldade é, por exemplo, conceber que a representação fracionária não é apenas uma superposição de números naturais e sim que esse novo número representa um quociente. Daí decorrem outras dificuldades, como aquelas relacionadas às frações equivalentes, isto é, ao entendimento de que uma fração pode ter infinitas e diferentes representações. Ou ainda aquelas relacionadas à ordenação de frações.
Nesse contexto, as questões que se colocam são: os estudantes de Pedagogia, que atuarão como professores dos anos iniciais ou como formadores de professores que atuarão nos anos iniciais, têm conhecimento da abrangência que deve ter o ensino de frações? Quais são as concepções que eles têm de frações e do seu ensino quando ingressam no curso de Pedagogia? A ementa da disciplina Matemática na Educação II e os recursos didáticos disponíveis são suficientes para uma formação que abarque os diversos significados atribuídos à representação fracionária?
Na tentativa de responder a essas questões, desenvolvemos uma ampla pesquisa, acompanhando a participação e o desempenho dos estudantes de duas turmas – uma de Bom Jesus do Itabapoana e outra de Barra do Piraí – ao longo do segundo semestre de 2015 na disciplina Matemática na Educação II. Tivemos como foco as situações problema e os questionamentos voltados para aspectos conceituais e metodológicos do ensino de frações constantes em fóruns online, avaliações a distância e avaliações presenciais.
Para este artigo, selecionamos a análise dos dados obtidos no fórum que dá início à disciplina, cujo objetivo principal foi resgatar as concepções prévias dos estudantes a respeito de frações. Assim, neste texto, em primeiro lugar, tratamos dos significados que podem ser atribuídos às frações. A seguir, abordamos ideias relevantes acerca da formação de professores e do uso de fóruns virtuais no ensino a distância. Na continuidade abrimos uma seção para descrever nosso método de pesquisa e outra para a análise a que nos propusemos. Por fim, à luz dos dados analisados, sinalizamos alguns elementos de base para a organização e realização da disciplina Matemática na Educação II.
Os significados das frações
O significado de fração como parte de um todo que foi dividido em partes iguais é o mais comum. Na escola, principalmente nos anos iniciais do Ensino Fundamental, esse significado é o mais abordado. Quando alguns professores introduzem o assunto partindo em pedaços iguais barras de chocolate, frutas, bolos e até pizzas, estão trabalhando o significado parte-todo. Contudo, esse significado não é o único. Vasconcelos e Belfort (2006, p. 5) identificam outros quatro significados associados à representação fracionária: medida, razão, quociente e operador.
O significado de fração como medida se assemelha ao parte-todo. Ele também trata da divisão de uma unidade em partes iguais; porém, em vez de destacar a parte, passamos a destacar pontos numa reta numérica.
Outro significado para as frações é a ideia de quociente da divisão de um número inteiro por outro diferente de zero. Por exemplo: se temos cinco barras de chocolate para dividir igualmente entre sete pessoas, a fração 5/7 representa o quociente que identifica quanto cada pessoa vai receber.
Também podemos associar frações ao significado de razão entre duas grandezas. Fazemos isso quando queremos comparar essas grandezas. Um exemplo desse significado pode ser visto quando se diz que o salário de uma pessoa é 1/2 do salário da outra.
Finalmente, o significado operador ocorre quando a fração assume o papel de transformar uma situação inicial para produzir uma situação final. Quando calculamos, por exemplo, uma fração de uma quantia, a situação inicial é a quantia, o operador é a fração e a situação final é a quantia correspondente a essa fração.
O domínio desses significados por parte dos professores é de suma importância para assegurar a qualidade do processo de ensino e aprendizagem. É transitando entre as diversas representações e os diversos significados associados às frações que os estudantes avançam no processo de construção de conceitos. Os professores precisam estar cientes desses significados para poder propor situações que envolvam todos eles e desafiem os estudantes.
A formação de professores
A formação de professores é um tema sobre o qual diversos educadores nacionais e internacionais têm se debruçado. Em nossa pesquisa sobre as concepções prévias de frações que têm os estudantes da Licenciatura em Pedagogia quando iniciam a disciplina Matemática na Educação II, apropriamo-nos das ideias de Tardif (2014), que aborda a questão dos saberes docentes, e de Serrazina (2003), Curi e Pires (2008), e Nacarato, Mengali e Passos (2013), que enfocam a formação de professores para o ensino de Matemática.
A função do professor vem passando por diversas transformações, que são resultado das mudanças nas concepções de escola e de construção de conhecimento. O Ministério da Educação (MEC) (2000) elenca uma série de exigências que se impõem ao exercício docente e, consequentemente, orientam a formação inicial de professores. Entre elas, tendo em vista nossos objetivos, destacamos:
- orientar e mediar o ensino para a aprendizagem dos estudantes;
- incentivar atividades de enriquecimento curricular; e
- elaborar e executar projetos para desenvolver conteúdos curriculares.
No que concerne ao ensino de Matemática, os PCN (1998) acrescentam:
Numa reflexão sobre o ensino da Matemática é de fundamental importância ao professor: identificar as principais características dessa ciência, de seus métodos, de suas ramificações e aplicações; [...] ter clareza de suas próprias concepções sobre a Matemática, uma vez que a prática em sala de aula, as escolhas pedagógicas, a definição de objetivos e conteúdos de ensino e as formas de avaliação estão intimamente ligadas a essas concepções (Brasil, 1997, p. 29).
O cumprimento dessas exigências, por sua vez, é influenciado pelos saberes docentes. Tardif (2014, p. 36) define saber docente “como um saber plural, formado pelo amálgama, mais ou menos coerente, de saberes oriundos da formação profissional e de saberes disciplinares, curriculares e existenciais” e considera como saberes disciplinares os correspondentes aos diversos campos do conhecimento ofertados na forma de disciplinas pelas instituições formadoras, sendo a Matemática um exemplo. Desse modo, a prática docente é influenciada pelos saberes construídos pelo professor não só nos bancos da universidade, mas ao longo de toda a sua vida. Suas experiências como estudante em todos os níveis de ensino, bem-sucedidas ou não, têm, por exemplo, poder determinístico em sua atuação profissional. Pesquisas como as de D’Ambrósio, Gonçalves e Peres (2013) constatam que muitos professores tendem a reproduzir as experiências que viveram como estudantes.
Para assegurar a formação de professores que contemplem as exigências atuais, é necessária uma formação que, além de focar nos conteúdos disciplinares, cause impacto sobre esses outros saberes, fazendo com que os estudantes os resgatem, avaliem-nos e, se necessário, reconstruam-nos, ampliando-os e aprofundando-os. Por isso, é importante identificar os conhecimentos prévios e os saberes dos estudantes dos cursos de licenciatura.
Trazendo essa reflexão para a formação de professores que ensinam Matemática, Serrazina (2003) sugere que os cursos de formação devem criar condições para que seu egresso seja:
- um facilitador da aprendizagem significativa dos alunos, gerando conhecimento escolar, uma vez que são os alunos que aprendem, e o professor deve ser capaz de criar as melhores condições para que isso aconteça;
- um investigador dos processos de ensino-aprendizagem que acontecem na sua turma, gerando assim conhecimento profissional;
- um constante construtor do currículo, conduzindo experiências com os seus alunos, refletindo sobre elas e reformulando-as;
- um gerador de conhecimento didático significativo ao investigar os processos de desenvolvimento do currículo (Serrazina, 2003, p. 69).
Cabe acrescentar que essas ideias não negligenciam a boa formação matemática para uma atuação qualificada. Concordamos com Curi e Pires (2008) quando salientam que “sem dominar, com um elevado grau de competência, o conteúdo que é suposto ensinar, o professor não pode exercer de modo adequado a sua função profissional” (Curi; Pires, 2008, p. 163). Nacarato, Mengali e Passos (2013) ressaltam, ainda, que “é na sala de aula que se manifestam não apenas o conhecimento do professor, mas também as suas concepções sobre a Matemática e o seu ensino, bem como o seu nível de confiança como professor que ensina Matemática”.
A Educação a Distância
Nossa concepção de EaD constitui-se com base nas contribuições agregadas dos trabalhos dos pesquisadores brasileiros Moran (2002), Belloni (2005), Preti (2009) e Borba, Malheiros e Amaral (2014).
Assumimos em nosso estudo que a EaD é uma modalidade sistematizada de educação, em que a aprendizagem acontece por interações mediadas tecnologicamente e o conhecimento é construído de forma colaborativa. Nossa concepção está em consonância com o conceito de EaD constante do Decreto nº 5.622, de 19 de dezembro de 2005:
modalidade educacional na qual a mediação didático-pedagógica nos processos de ensino e aprendizagem ocorre com a utilização de meios e tecnologias de informação e comunicação, com estudantes e professores desenvolvendo atividades educativas em lugares ou tempos diversos (Brasil, 2005, p. 1).
Nesse cenário educacional virtual figuram alguns atores, cujos perfis são caracterizados por Campos, Roque e Amaral (2007):
em cursos online, os participantes, sejam alunos ou tutores, ficam cientes de que, além das habilidades relacionadas ao uso do computador, também precisam possuir as seguintes competências para o estudo: capacidade de aprendizagem ativa; capacidade de convivência; capacidade de gerenciar seu horário; organização e responsabilidade (Campos; Roque; Amaral, 2007, p. 46).
Refletindo sobre os estudantes da EaD sujeitos de nossa pesquisa, entendemos que eles precisam desenvolver uma postura consciente de que o processo de aprendizagem é centrado neles e se preocupar com a construção do conhecimento de forma autônoma e disciplinada, o que é sinalizado por Belloni (2005, p. 191).
Nos ambientes virtuais de aprendizagem (AVAs) – plataformas digitais sistematicamente estruturadas como espaço educativo online, viabilizadoras dos recursos tecnológicos para a consecução dos processos de ensino-aprendizagem nos cursos em EaD –, o conhecimento é construído de forma colaborativa, mediante a interação entre pares virtuais – professores, orientadores/mediadores/tutores e alunos.
Partilhamos do entendimento de Belloni (2003 apud Borba; Malheiros; Amaral, 2014, p. 27-28), quando considera que o conceito de interação tem caráter sociológico, constituindo-se num processo relacional caracterizado pela presença de, pelo menos, dois sujeitos cujo relacionamento pode se dar de forma síncrona ou assíncrona. Assim, defendemos que a interação é componente essencial para a construção de conhecimentos num espaço educativo – especialmente o online –, à medida que os atores contribuam se posicionando linguisticamente em um ambiente colaborativo e respeitoso, em que o equilíbrio e o entendimento das ações comunicativas prevaleçam.
Outro fato que merece destaque nesta discussão sobre interação é que o processo de comunicação nos espaços educativos mudou, passando de unidirecional – típico do ensino tradicional – para, como ressalta Moran (2014), “bidirecional e multidirecional”. Segundo esse autor, hoje
o professor fala com todos, todos falam com ele e entre si e cada aluno pode falar com o outro. É uma comunicação múltipla, diversificada, flexível, muito rica e cheia de surpresas, porque cada interação modifica a resposta seguinte, cada contribuição (Moran, 2014, p. 55).
Na educação a distância, essa dinâmica interativa é bastante evidente, constituindo-se como fundamental para a aprendizagem e como uma marca identitária substancial.
Para efetivação desse processo comunicativo na EaD, existem elementos tecnológicos disponíveis que podem ser mobilizados pedagogicamente para favorecer interações entre sujeitos em diferentes espaços geográficos, podendo ser classificadas em relação à temporalidade como síncronos (tempo real; por exemplo, chat e videoconferência) e assíncronos (tempo diferido, como em fórum virtual, blog e e-mail), sendo o fórum virtual – que alguns teóricos denominam também como fórum eletrônico de discussão, lista de discussão ou, simplesmente, lista – o instrumento de nossa investigação.
Segundo Segenreich (2005), os fóruns de discussão são usados de diversas formas no ambiente acadêmico; uma delas é para “desenvolvimento do ensino em ambientes virtuais de aprendizagem, propiciando integração, sentimento de pertença, trocas, questionamentos e elaborações colaborativas”. Esse componente tecnológico de aprendizagem constitui-se em um espaço privilegiado de debates sobre assuntos de interesse ou sobre determinados conteúdos, com grande potencial interativo e de comunicação.
O método de pesquisa
Em linhas gerais, nossa pesquisa teve caráter qualitativo. Segundo Godoy (1995, p. 63), quando se utiliza esse tipo de abordagem, o pesquisador está preocupado “com o processo e não simplesmente com os resultados ou produto”. A autora ainda pontua que “quando o estudo é de caráter descritivo e o que se busca é o entendimento do fenômeno como um todo, na sua complexidade, é possível que uma análise qualitativa seja a mais indicada” (Godoy, 1995, p. 63).
Com esse posicionamento, retomamos a questão que tentamos responder neste artigo: quais as concepções sobre as frações e seu ensino que os estudantes de Pedagogia têm ao iniciar a disciplina Matemática na Educação II?
O curso de licenciatura em Pedagogia onde realizamos a pesquisa é o curso a distância oferecido pela Universidade Federal do Estado do Rio de Janeiro (UniRio) sob a administração do Consórcio Cederj. Nosso público-alvo foi composto pelos estudantes dos polos de Bom Jesus do Itabapoana e Barra do Piraí que estavam inscritos para cursar a disciplina Matemática na Educação II no segundo semestre de 2015. Cada grupo tinha nove estudantes.
O curso de licenciatura em Pedagogia possui duas disciplinas voltadas para a compreensão de conteúdos e métodos de ensino de Matemática: Matemática na Educação I e Matemática na Educação II. É justamente nas aulas iniciais desta segunda que os principais conceitos e métodos de ensino associados às frações são trabalhados. Por isso, tendo em vista identificar as concepções que os estudantes já possuíam, iniciamos as aulas com o fórum cujas participações são o centro de nossa análise. Na figura a seguir, apresentamos a tela propositiva, onde os estudantes têm acesso às questões e devem interagir e postar contribuições.
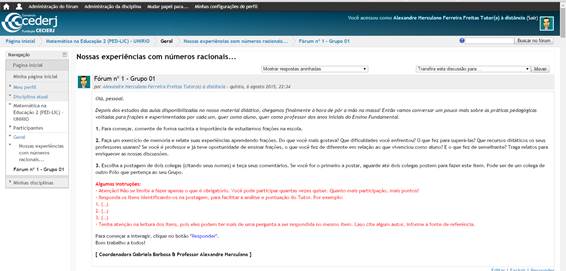
Figura 1: Tela do Fórum com as questões propostas para discussão
Fonte: dados da pesquisa.
Como pode ser observado, o fórum foi aberto em 16 de agosto de 2015 e esteve disponível por 16 dias. Ao final desse período, contamos 19 postagens. É importante observar que nem todos os estudantes participaram, fato que posteriormente foi esclarecido pela dificuldade de acesso que alguns ainda apresentavam. Não nos foi difícil realizar a pesquisa, pois atuamos como professor e coordenadora da disciplina. Confirmamos o que já é sabido: “muitas vezes, as questões de pesquisa se originam na própria prática profissional do pesquisador” (Morse, 1994 apud Araújo; Borba, 2013, p. 34).
A análise de dados
Antes de iniciar a análise do material coletado, cabe registrar que escolhemos como embasamento teórico a Análise de Conteúdo (AC) descrita por Bauer (2002). Segundo esse autor, ela é “uma técnica para produzir inferências de um texto focal para seu contexto social de maneira objetivada” (Bauer, 2002, p. 191). Em síntese, trata-se de uma metodologia de análise textual que sugere a criação de categorias para a classificação dos textos.
Após examinarmos e catalogarmos os 19 registros do fórum, elaboramos três categorias para orientar nossa análise. São elas:
- relato de experiência pessoal;
- concepções de fração; e
- métodos para o ensino de frações.
A primeira, que abarcou onze registros, corresponde aos textos em que os autores enfatizaram suas experiências como estudantes dos anos iniciais, quando aprenderam frações pela primeira vez. A segunda, que teve quatro registros, corresponde aos textos em que os autores evidenciaram os significados que atribuem às frações. Finalmente, a terceira, que também contou com quatro registros, contém os textos em que os autores dão sugestões de métodos para o ensino de frações. É importante esclarecer que, embora apenas os textos da segunda categoria apresentem claramente as concepções que os estudantes têm de frações, os textos da terceira categoria também sinalizaram tais concepções.
Afinal, a escolha que o professor (ou futuro professor, no caso de nossos estudantes pesquisados) faz de um método de ensino esboça, ainda que indiretamente, a concepção que ele tem do conteúdo a ser ensinado. Como mencionamos anteriormente, conteúdo e método se integram e se articulam às experiências pessoais, compondo o saber docente. Sendo assim, do mesmo modo, ao revelarem suas experiências pessoais (categoria 1), os sujeitos também deram indícios de suas concepções.
Na análise da primeira categoria, chamou nossa atenção o medo da Matemática e, mais especificamente, das frações que os estudantes revelaram. O texto a seguir, produzido pela estudante G, é um exemplo.
Aprender frações realmente é muito importante, mas para nós é mais fácil ver isso agora quando adultos, não acha? Quando eu era criança não pensava assim, tinha pavor de ouvir falar em frações, números decimais, até aprendê-los e ver que não eram o bicho de sete cabeças que eu mesma pintei. Por fazer parte desse ensino tradicionalista, rigoroso e nada criativo de antes, criei certa aversão à disciplina.
Como podemos observar, a estudante reconhece a importância do estudo das frações desde os anos iniciais, no entanto relata que as dificuldades que vivenciou na aprendizagem das frações conduziram a certa aversão à Matemática. De acordo com Tardif (2014), nesse texto é possível verificar dois saberes: um existencial – a Matemática é difícil – fruto de experiências malsucedidas com a disciplina desde os anos iniciais, e um saber disciplinar – o que são as frações, sua relação com números decimais e suas aplicações. Além disso, a estudante faz uma crítica ao ensino tradicional, mas não identifica claramente outras possibilidades de ensino. Isto nos sugeriu a abordagem de novas metodologias de ensino em nossa disciplina.
Também criticando o ensino tradicional e sinalizando um ensino alternativo com ênfase nas representações gráficas e no uso de materiais manipulativos (formas de pizza e de bolo, por exemplo), o texto a seguir foi classificado na segunda categoria, pois nele constam duas concepções distintas da autora sobre frações.
Bom dia, me chamo L. e estou no 4º período do curso de Pedagogia. 1 - É muito importante aprendermos a fazer uso de frações, até mesmo porque a usamos em nosso dia a dia em diversas situações, como, por exemplo, quando temos uma certa quantia em dinheiro e queremos dividi-la para pagarmos nossas contas, ou também quando vamos preparar um bolo, um pudim ou um almoço e nos deparamos com medidas de 1/2 xícara de leite, de açúcar, de farinha de trigo, e assim por diante, portanto é impossível não fazer o uso das frações em nosso cotidiano. 2 -Lembro-me de que tinha muita dificuldade em aprender fração, afinal a Matemática era uma disciplina que me causava muita tristeza, pois minhas dificuldades eram enormes. Minha professora sempre teve muita paciência para me ensinar, ela usava os desenhos em forma de pizza, de bolo, e eram bem coloridos para chamar a atenção dos alunos, eu adorava os desenhos, mas não gostava das atividades. Não sou professora, mas acho que hoje ainda é muito difícil para os alunos, porém hoje os recursos são maiores, além de que os mesmos podem pesquisar em vários sites educacionais as suas dúvidas, não ficando presos apenas ao material didático.
Certamente esse texto também se enquadra nas outras duas categorias. A estudante relata suas primeiras experiências na aprendizagem de frações e menciona em linhas gerais recursos didáticos para o ensino, revelando seus saberes disciplinares e existenciais. No entanto, dada a nossa preocupação principal com os significados que os estudantes atribuem às frações, enquadramos esse texto na segunda categoria. É fácil perceber que, dos significados que apresentamos anteriormente, encontramos os de quociente – “quando temos uma certa quantia em dinheiro e queremos dividi-la para pagarmos nossas contas” – e medida – “quando vamos preparar um bolo, um pudim ou um almoço e nos deparamos com medidas de 1/2 xícara de leite, de açúcar, de farinha de trigo, e assim por diante”.
É essencial observar que a estudante não diferencia os significados, abordando frações de forma generalizada. Isso sinaliza a necessidade de um trabalho intensivo acerca desses significados ao longo da disciplina. Trata-se de um saber profissional (Tardif, 2014) que contribuirá para que esses estudantes de Pedagogia se tornem, de fato, facilitadores da aprendizagem significativa, tal como Serrazina (2003) propõe. A postagem a seguir também destaca esses dois significados:
Bom dia a todos!
1 - É importante estudar frações na escola, pois através delas a professora irá conscientizar os alunos de que fração está ligada a certas situações da divisão, ou seja, fração é um todo sendo dividido em partes, por exemplo, um bolo de 12 fatias dividido para oito crianças, uma pizza de seis pedaços dividida por quatro pessoas, também uma metade, um terço, um quarto é fração, muito utilizada nas receitas de um bolo por exemplo. Portanto, a fração está no dia a dia de todos e precisa ser estudada em sala de aula com as crianças desde já.
Diferentemente do anterior, esse texto se enquadra apenas na segunda categoria. A autora se deteve em aspectos conceituais das frações, revelando saberes disciplinares (Tardif, 2014) sem, contudo, expressar suas experiências passadas ou sugerir metodologias de ensino. O significado quociente é facilmente identificado em “um bolo de 12 fatias dividido para oito crianças, uma pizza de seis pedaços dividida por quatro pessoas”, e o significado medida em “uma metade, um terço, um quarto é fração, muito utilizada nas receitas de um bolo”. Com apenas uma exceção, em todas as postagens da segunda categoria e mesmo nas informações implícitas nas outras categorias, os significados observados foram quociente e medida. A exceção foi o significado parte-todo observado apenas na seguinte postagem:
Oi, L. Eu compartilho a situação sua, a Matemática me causa tristeza, e sobre as frações a gente sabe que é um todo dividido em partes, e que vemos em vários lugares um meio, um quarto, então as crianças têm que aprender a ler e interpretar as frações porque elas estão presentes no mundo.
Cabe observar nesse texto que a autora escreveu o conceito de fração com o significado parte-todo, sem oferecer exemplos. Diante disso, inferimos que o estudante já compreendesse os conceitos de Matemática num nível de abstração mais elevado que seus colegas de turma, porém isso não foi confirmado pelas participações da aluna ao longo da disciplina.
Assim, os significados operador e razão não foram mencionados pelos estudantes. É evidente que postagens em um fórum introdutório da disciplina não são suficientes para generalizar resultados ou afirmar que medida, parte-todo e quociente são os únicos significados que eles conhecem. Contudo, a ausência de dois significados importantes e o fato de ninguém ter se referido a mais de dois significados sugerem a necessidade de um trabalho mais aprofundado sobre esse assunto. Afinal, concordamos com Curi e Pires (2008) quando reforçam a importância de o professor dominar os conteúdos a serem ensinados, se quisermos garantir um ensino de qualidade.
Tendo em vista criar condições para que os estudantes compreendessem os significados associados às frações e pretendendo propor uma formação que impactasse seus saberes existenciais, tal como propõe D’Ambrósio, Gonçalves e Peres (2013), iniciamos as aulas da disciplina com otimismo. Os registros da primeira categoria aliados aos da terceira, exemplificados na postagem a seguir, revelavam que os estudantes ansiavam por novos métodos de ensino.
Concordo com a G. e a L., pois a fração está presente na vida de todos nós; exemplos: preparação dos alimentos, estatística, pagamentos etc.
Em tempos passados era tudo na base do decoreba, o aluno poucas vezes argumentava sobre os assuntos principalmente sobre Matemática. Com o passar dos tempos, a disciplina passou a ser vista com outros olhos, onde o aprender é realizado com prazer.
O conteúdo nos leva a buscar, não de uma maneira forçada, mas sim prazerosa, através de jogos, experiências, brincadeiras, de maneira lúdica onde o aprender é para a vida.
Verificamos que a estudante destaca a importância da contextualização e das atividades lúdicas nas aulas sobre frações. Entendemos, assim como Nacarato, Mengali e Passos (2013), que é na prática de sala de aula que se pode reconhecer as concepções que o professor tem da Matemática e do seu ensino. Assim, reconhecemos na proposta de aula apresentada por essa estudante que sua concepção de Matemática é bastante diferente daquela que subjaz às práticas tradicionais.
Considerações finais
Neste artigo, tivemos como objetivo identificar e analisar as concepções de fração que os estudantes do curso de Pedagogia EaD da UniRio apresentaram no fórum inicial da disciplina Matemática na Educação II. Diante dos resultados apresentados, verificamos que os estudantes mencionaram apenas os significados parte-todo, medida e quociente, porém revelaram anseio por métodos de ensino que envolvam atividades lúdicas, tornando o processo de aprendizagem mais prazeroso. Embora esses dados não possam ser generalizados, eles foram de suma importância para que determinássemos os caminhos que seguiríamos na abordagem de frações. Entre os aspectos que decidimos privilegiar, ressaltamos:
- a ênfase num ensino contextualizado com exemplos de variadas situações em que se aplicam os conhecimentos de frações;
- a compreensão dos diferentes significados atribuídos às frações por meio da comparação de classes de situações; e
- a análise de materiais manipulativos e atividades lúdicas para o ensino das frações.
Por fim, ao colocarem no fórum suas respostas às questões propostas, os estudantes estabeleceram um ambiente favorecedor tanto de suas aprendizagens como também das dos colegas de forma colaborativa. Numa reflexão mais ampla, podemos constatar que o fórum virtual é uma ferramenta tecnológica que potencializa a aprendizagem e que favoreceu a construção de conhecimentos.
Referências
ARAÚJO, J. L.; BORBA, M. C. Construindo pesquisas coletivamente em Educação Matemática. In: BORBA, M. C.; ARAÚJO, J. L. (Orgs.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2013. p. 31-51.
BAUER, M. W. Análise de conteúdo clássica: uma revisão. In: BAUER, M. W.; GASKELL, G. Pesquisa qualitativa com texto, imagem e som: um manual prático. 3ª ed. Petrópolis: Vozes, 2002. p. 189-217.
BELLONI, M. L. Educação a distância e inovação tecnológica. Trabalho, Educação e Saúde, Rio de Janeiro, v. 3 nº 1, p. 187-198, mar. 2005. Disponível em: http://www.scielo.br/pdf/tes/v3n1/10.pdf. Acesso em 29 ago. 2015.
BORBA, M. C.; MALHEIROS, A. P. S.; AMARAL, R. B. Educação a Distância online. Belo Horizonte: Autêntica, 2014.
BRASIL. Decreto 5.622, de 19 de dezembro de 2005. Regulamenta o Art. 80 da Lei no 9.394, de 20 de dezembro de 1996, que estabelece as diretrizes e bases da educação nacional. Disponível em: http://www.uab.capes.gov.br/images/stories/downloads/legislacao/decreto5622.pdf. Acesso em 19 jul. 2015.
______. MINISTÉRIO DA EDUCAÇÃO. Proposta para diretrizes para formação inicial de professores da Educação Básica em cursos de nível superior. Brasília, 2000.
______. MINISTÉRIO DA EDUCAÇÃO. SECRETARIA DE EDUCAÇÃO FUNDAMENTAL. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1998. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf. Acesso em 20 jul. 2015.
CAMPOS, G. H. B.; ROQUE, G. O.; AMARAL, S. B. Dialética da educação a distância. Rio de Janeiro: PUC-Rio, 2007, 96 p.
CURI, E.; PIRES, C. M. C. Pesquisas sobre a formação do professor que ensina Matemática por grupos de pesquisa de instituições paulistanas. Revista Educação Matemática Pesquisa, São Paulo, v. 10, nº 1, p. 151-189, 2008. Disponível em: http://revistas.pucsp.br/index.php/emp/article/viewFile/1655/1065. Acesso em 20 jul. 2015.
D'AMBROSIO, B. S.; GONCALVES Jr., M.; PERES, G. Simulações na aprendizagem de conceitos matemáticos com futuros professores das séries iniciais. Educação Matemática em Foco (UEPB), v. 2, p. 100-127, 2013.
GODOY, A. S. Introdução à pesquisa qualitativa e suas possibilidades. Revista de Administração de Empresas, São Paulo, v. 35, nº 2, p. 57-63, mar./abr. 1995. Disponível em: http://www.scielo.br/pdf/rae/v35n2/a08v35n2.pdf. Acesso em 05 out. 2015.
MORAN, J. M. M. O que é educação a distância. 2002. Disponível em: http://www2.eca.usp.br/moran/wp-content/uploads/2013/12/dist.pdf. Acesso em 29 ago. 2015.
______. Autonomia e colaboração em um mundo digital. Revista Educatrix, São Paulo, Moderna, ano 4, nº 7, p. 52-37, 2014. Disponível em: http://www.moderna.com.br/educatrix/ed7/educatrix7.html?pag=1. Acesso em 27 nov. 2015.
NACARATO, A. M.; MENGALI, B. L. S.; PASSOS, C. L. B. A Matemática nos anos iniciais do Ensino Fundamental: tecendo fios do ensinar e do aprender. 2ª ed. Belo Horizonte: Autêntica, 2013.
PRETI, O. Educação a Distância: fundamentos e políticas. Cuiabá: EdUFMT, 2009.
SEGENREICH, S. C. D. O fórum de discussão como espaço de pesquisa para análise de questões curriculares. Série Estudos – Periódico do Mestrado em Educação da UCDB. Campo Grande, nº 7, p. 52-37, jan./jun. 2005.
SERRAZINA. L. A formação para o ensino da Matemática: perspectivas futuras. Educação Matemática em Revista, SBEM, ano 10, nº 14, p. 67-73.
TARDIF, M. Saberes docentes e formação profissional. Petrópolis: Vozes, 2014.
VASCONCELOS, C. B.; BELFORT, E. Diferentes significados de um mesmo conceito: o caso das frações. Pró-Letramento Matemática. Rio de Janeiro: LIMC, 2006.
Leia mais sobre Inclusão e tecnologias em Educação Matemática
Publicado em 20 de dezembro de 2016
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

