Recursos e adaptação de materiais didáticos para a inclusão de alunos com deficiência visual no ensino de Matemática

Professor do Instituto Benjamin Constant

Introdução

A inclusão de alunos com necessidades especiais no sistema regular de ensino é hoje a diretriz principal das políticas públicas educacionais, tanto a nível federal, quanto estadual e municipal (Ferreira e Glat, 2003; Glat, Ferreira, Oliveira e Senna, 2003).

Este trabalho tem como objetivo apresentar recursos básicos e essenciais que possibilitem práticas pedagógicas inclusivas e adequadas destinadas ao ensino de Matemática para alunos com deficiência visual incluídos nas escolas regulares. Propõe-se também a incentivar a produção de material adaptado de baixo custo e a utilização de metodologias e procedimentos didáticos que possam servir de auxílio aos professores que tenham o enorme de desafio de ensinar Matemática a alunos cegos e com baixa visão. O trabalho é o resultado de estudos e pesquisas realizados no âmbito do Instituto Benjamin Constant, uma escola especializada no ensino de alunos cegos e com baixa visão, em turmas do segundo segmento do Ensino Fundamental nos anos de 2014 e 2015. Os recursos, métodos e materiais apesentados a seguir mostraram-se indispensáveis às aulas de Matemática e tornaram as aulas dinâmicas, práticas e experimentais, possibilitando que os alunos tornassem parte integrante do processo de ensino e aprendizagem.

De acordo com a epígrafe, as questões relacionadas ao ensino e aprendizagem de pessoas com deficiências, em particular os alunos cegos e com baixa visão, expostas no trabalho a seguir tornaram-se, nos últimos anos, importante objeto de estudo e investigação.

Para Santos (2004),

por “orientação inclusiva” entendemos os esforços empreendidos pela instituição educacional no sentido de minimizar, ou eliminar, as barreiras que estudantes podem sofrer e que os impeçam de participar plenamente da vida acadêmica devido à desvalorização de suas diversidades oriundas de gênero, etnias, condições sociais, situações familiares, religião, habilidades acadêmicas etc. (p. 1).

Com a Lei Brasileira de Inclusão (2016), que assegura a oferta de sistema educacional inclusivo em todos os níveis e modalidades de ensino e a adoção de projetos pedagógicos que institucionalizem o atendimento educacional especializado, o Instituto Benjamin Constant (IBC) ganha papel importante nesse processo, visto que é um grande laboratório de pesquisas, estudos, experiências e práticas. Com 162 anos de existência, o instituto se fortalece e se consolida no cenário nacional como uma instituição que pode e deve ter papel de protagonismo no apoio às demais instituições de ensino. De acordo com Art. 34 do Anexo I do Decreto n° 7.690, de 02 de março de 2012, são competências do IBC:

III - promover e realizar programas de capacitação dos recursos humanos na área de deficiência visual;
IV - promover, realizar e divulgar estudos e pesquisas nos campos pedagógico, psicossocial, oftalmológico, de prevenção das causas da cegueira, de integração e de reintegração de pessoas cegas e de visão reduzida à comunidade;
V - promover programas de divulgação e intercâmbio de experiências, conhecimentos e inovações tecnológicas na área de atendimento às pessoas cegas e de visão reduzida;
VI - elaborar e produzir material didático-pedagógico para o ensino de pessoas cegas e de visão reduzida;
VII - apoiar técnica e financeiramente os sistemas de ensino e as instituições que atuam na área de deficiência visual;
VIII - promover desenvolvimento pedagógico visando ao aprimoramento e a atualização de recursos instrucionais.

Nesse sentido, o presente trabalho, resultado de estudos, pesquisas e práticas desenvolvidas pelo autor no âmbito do IBC, tem por finalidade apresentar recursos básicos, práticas pedagógicas adequadas, incentivo à produção de material adaptado de baixo custo, metodologias e procedimentos didáticos que possam servir de auxílio aos professores para o trabalho com alunos com deficiência visual (DV) incluídos nas escolas regulares.

Bernardo (2016) cita que, ao trabalhar com alunos deficientes visuais, o professor deve fazer das aulas momentos de diálogo, em que as trocas e experimentações são fundamentais não só para seguir as diversas orientações didáticas contidas nos Parâmetros Curriculares Nacionais (PCN), mas também porque essa metodologia que coaduna diálogo, troca de experiências, experimentos e materiais adequados é fundamental para o aprendizado desse alunado.

No que se refere ao ensino de Matemática, a experimentação tátil é particularmente importante, pois permite que o estudante possa ter contato com diferentes e concomitantes formas de percepção qualitativa e quantitativa, de manuseio, observação, confronto, dúvida e de construção conceitual. “A experimentação permite ainda ao aluno a tomada de dados significativos, com os quais possa verificar ou propor hipóteses explicativas e, preferencialmente, fazer previsões sobre outras experiências não realizadas” (Brasil, 2000, p. 53).

Recursos básicos e essenciais destinados ao ensino de Matemática para DV

O uso de materiais e recursos deve se caracterizar pelo envolvimento dos alunos em uma situação de aprendizagem ativa. Segundo Passos (2012), eles devem servir de suporte experimental na organização do processo de ensino e aprendizagem e como mediadores para facilitar a relação professor-aluno-conhecimento, sempre que um saber estiver sendo construído.

Usando o Braille

O primeiro recurso que descreveremos aqui é a utilização correta do sistema Braille para o ensino de Matemática. Em 2006, a Comissão Brasileira do Braille e a Comissão de Braille de Portugal elaboraram um manual intitulado Código Matemático Unificado para a Língua Portuguesa (CMU). De acordo com o CMU (Brasil, 2006), a aplicação do Sistema Braille à Matemática foi proposta por Louis Braille em sua primeira versão em 1837. Nessa ocasião, foram apresentados os símbolos fundamentais para os algarismos e as convenções para Aritmética e Geometria. No entanto, essa simbologia nem sempre foi adotada nos países que vieram a utilizar o sistema Braille, por questões e diferenças regionais e locais. Ainda conforme o CMU (Brasil, 2006), em 1929 realizou-se na cidade de Viena um congresso reunindo países da Europa e os Estados Unidos com o intuito de criar um documento que pudesse unificar a simbologia Braille para a Matemática. Apesar desse esforço, as diferenças prevaleceram e não foi possível firmar um acordo que pudesse estabelecer um documento unificado.

Com a evolução técnica e a explosão científica ocorridas no século XX, essas diferenças aumentaram, e a necessidade de estabelecer um documento único tornou-se mais urgente. De lá para cá, diversas comissões, comitês e eventos foram realizados, todos imbuídos da construção desse documento. Por fim, em 2006, o Brasil foi contemplado com a versão final, hoje utilizada em diversos países.

O Código Matemático Unificado para a Língua Portuguesa oferece excelentes opções para a representação de símbolos do sistema comum até agora sem representação adequada no Sistema Braille, como os casos de índices e marcas. Alternativa digna de destaque é a aplicação dos parênteses auxiliares, recurso de representação em Braille nos casos em que a escrita linear dificulta o entendimento das expressões matemáticas (Brasil, 2006, p. 15).

Em uma perspectiva de inclusão, seja no ensino básico, técnico ou superior, o CMU é uma ferramenta indispensável e fundamental para o ensino de Matemática para alunos cegos. De forma simplificada, a escrita no Sistema Braille se dá em uma cela com seis pontos, como está na Figura 1.

Figura 1: Alfabeto Braille
Disponível em: http://www.alfabeto.net.br/alfabeto-Braille/

Para a escrita matemática em Braille, o CMU apresenta orientações adequadas que vão desde a simbologia matemática mais simples, frações, expressões numéricas e algébricas até as mais avançadas, como derivadas, integrais, simples, duplas e triplas. Algumas dessas expressões podem ser observadas na Figura 2.

Figura 2: Equações matemáticas representadas em tinta e Braille.
Fonte: Código Matemático Unificado (Brasil, 2006, p. 51).

Para o professor com pouca vivência na escrita Braille, há disponível o software livre Braille Fácil, que possibilita a conversão de textos escritos em língua portuguesa para o Sistema Braille. Dessa forma, os textos e materiais podem ser impressos em Braille para o aluno cego, permitindo assim acessibilidade aos conteúdos das aulas, livros e materiais disponíveis aos alunos videntes.

O soroban

O segundo recurso essencial para o ensino de Matemática para alunos com DV é o soroban, um tipo de ábaco japonês, comumente utilizado por alunos cegos devido à impossibilidade do registro das operações matemáticas em tinta por parte desses alunos (Bernardo, 2015). Não é só um instrumento de registro; o soroban é importante para o desenvolvimento do raciocínio, estimulando a criação de habilidades mentais (Brasil, 2009), sendo muitas vezes confundido, de forma equivocada, com uma calculadora; o instrumento não é o responsável pelos cálculos, mas sim o praticante. Sendo assim, esse instrumento revela-se fundamental para o desenvolvimento das estratégias para o ensino das operações fundamentais a alunos cegos e com baixa visão, operações imprescindíveis à resolução de problemas de diversas naturezas (Bernardo, 2015).

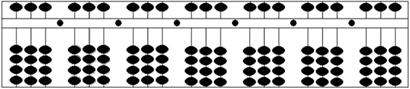
Figura 3: Modelo de soroban utilizado pelos alunos no IBC
Disponível em: http://www2.td.utfpr.edu.br/semat/AS.pdf

O soroban possibilita que os alunos façam registros numéricos, realizem as quatro operações fundamentais; com ele, também é possível avançar para as operações com números inteiros, racionais, raiz quadrada, cálculo do mínimo múltiplo comum (MMC) e máximo divisor comum (MDC). Sendo assim, essa ferramenta deve ser cotidianamente utilizada e explorada por professores que possuam alunos com DV, a fim de que esses alunos possam participar das aulas de Matemática de forma menos excludente, como um mero ouvinte, receptor de informações.

Um breve exemplo de sua utilização pode ser observado no cálculo do MMC. Digamos que em dado momento o aluno necessite calcular o MMC(12, 15, 18) e que sinta dificuldade de utilizar o cálculo mental para obter o resultado. O cálculo pode ser realizado da seguinte forma:

1) Registram-se os três números nas três primeiras classes, conforme a Figura 4:

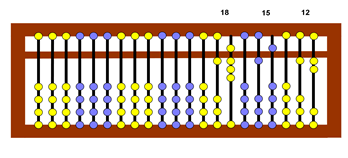
Figura 4: Registro dos números 12, 15 e 18

2) Em seguida, coloca-se o primeiro número primo na sétima classe e, ao efetuarmos a divisão, os resultados devem substituir os números 12, 15 e 18, iniciais.

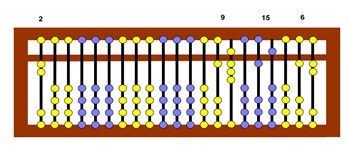
Figura 5: Registro dos números 9, 15 e 6, resultado da
divisão dos números iniciais por 2.

3) Os próximos fatores primos deverão ser colocados ao lado do número 2, na sétima classe, e os resultados das divisões darão lugar aos números iniciais na primeira, segunda e terceira classes, até que se encontre o número, conforme fazemos em tinta. O registro pode ser observado na Figura 6.

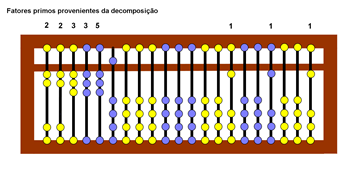
Figura 6: Registro dos fatores primos provenientes
da decomposição dos números 12, 15 e 18

4) Por fim, basta concluir que o MMC (22.32.5) = 90.

Ao identificarmos o soroban como uma ferramenta importante e um aliado do aluno e do professor nesse processo, estamos corroborando as ideias de Ferronato (2002, p. 48), que argumenta que “o professor não precisa mudar seus procedimentos quando tem um aluno deficiente em sua sala de aula, mas apenas intensificar o uso de materiais concretos para ajudar na abstração dos conceitos”.

Avançando na utilização e adaptação dos recursos para o ensino de Matemática para alunos com DV, acredito que a criatividade e a vontade em tornar as aulas acessíveis, participativas e inclusivas são mais importantes do que o conhecimento técnico da produção de materiais. A utilização de materiais concretos/táteis tem por objetivo possibilitar o primeiro “contato” do aluno com o conteúdo a ser estudado.

Passos (2012) afirma que esses materiais devem servir de suporte experimental na organização do processo de ensino e aprendizagem e como mediadores para facilitar a relação professor-aluno-conhecimento sempre que um saber estiver sendo construído.
Fiorentini e Miorim (1990) esclarecem que o uso de recursos e materiais não pode se justificar somente por serem motivadores, por tornarem as aulas mais “alegres” ou para que os alunos passem a “gostar de Matemática”, pois “por trás de cada material se esconde uma visão de educação, de Matemática, do homem e de mundo” (p. 2).

Ao adaptar e/ou produzir um material, o professor deve ter como princípio possibilitar que o aluno com DV, seja ele cego ou com baixa visão, possa vivenciar e experimentar o conteúdo. De acordo com Bernardo (2016, p. 3),

o ensino de Matemática, conforme se apresenta nos dias atuais nos livros didáticos, recorre a um grande apelo visual em suas páginas. São figuras, fotografias, desenhos e oferta de material em CD-ROM para atrair professores e alunos. Todo esse aparato, não apropriado aos deficientes visuais, acaba por aumentar e evidenciar o quão excludente pode ser o ensino nas escolas regulares.

Nesse sentido, o material deve ser pensado de forma que todos possam ser beneficiados. Produzir algo que seja utilizado somente pelo aluno com deficiência visual significa excluí-lo do contexto da aula, deixando-o, mais uma vez, em segundo plano, isolado das atividades trabalhadas pelos demais.

Estudando frações

Um conteúdo importante que se apresenta nos livros didáticos de forma bastante visual é o reconhecimento das frações em figuras planas dividas em partes iguais. Nesse caso, o aluno vidente é capaz de realizar as atividades propostas sem maiores dificuldades, beneficiando-se apenas de sua visão e, ainda que apresente alguma dificuldade, o professor pode utilizar-se do quadro para construir novas figuras e/ou esclarecer as possíveis dúvidas e dificuldades apresentadas. Entretanto, o aluno com deficiência visual necessita que esse material seja adaptado à compreensão do conteúdo. Nesse contexto, proponho aqui um material simples e de baixo custo que pode auxiliar o professor no trabalho com frações e até em outros conteúdos, tais como reconhecimento dos polígonos, nomenclatura, vértices, lados, ângulos etc.

Foram construídas figuras geométricas seccionadas em partes iguais, divididas com barbante e fixadas em papel cartão com cola branca. Os polígonos e círculos foram construídos no Geogebra, para que a precisão das divisões fosse a melhor possível, mas podem ser construídos com régua e compasso, como podemos observar na Figura 7.

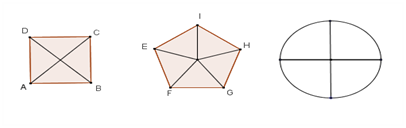
Figura 7: Polígonos e círculo construídos no software Geogebra

Em seguida, utilizou-se o material etil vinil acetato (EVA), com duas texturas e quatro cores diferentes, cortando-o para obter as partes desejadas e, posteriormente, colando-as no papel cartão para formar os polígonos, como está na Figura 8.

Em seguida, utilizou-se o material etil vinil acetato (EVA), com duas texturas e quatro cores diferentes, cortando-o para obter as partes desejadas e, posteriormente, colando-as no papel cartão para formar os polígonos, como está na Figura 8.

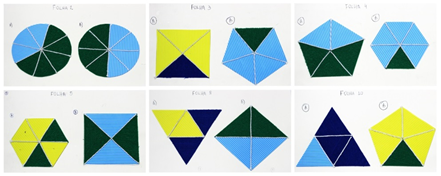
Figura 8: Figuras geométricas construídas em EVA
Fonte: Arquivo pessoal do autor.

Esse material foi utilizado e testado, em 2015, em uma turma do 6º ano do Ensino Fundamental do IBC, que possuía onze alunos, sendo quatro com baixa visão e sete cegos. O material teve como objetivo proporcionar ao aluno com DV um primeiro “contato” com o conteúdo. Iniciamos a aula com uma discussão sobre o material e o conteúdo, e os alunos receberam também uma lista (em Braille e em tinta) com uma problematização para ser trabalhada junto ao material, assim como é feito em turmas regulares. É importante notar que, em turmas regulares, as mesmas figuras podem estar nos livros ou podem ser desenhadas no quadro pelo professor, mas em ambos os casos o aluno com DV, ao utilizar o material, não será excluído da atividade.

O reconhecimento das diferentes necessidades educacionais especiais dos alunos é um passo inicial e representa um grande desafio ao professor, pois adaptar, (re)construir estratégias e metodologias requer estudo, planejamento, condições adequadas e apoio institucional. Nesse sentido, propõem-se aqui materiais simples, de baixo custo, que podem inclusive ser feitos pelos próprios alunos com a devida orientação do professor.

Figura 9: Alunos utilizando o material
Fonte: Arquivo pessoal do autor

A utilização de materiais e estratégias diferenciadas não representa garantia de aprendizado, mas possibilita aulas mais interessantes, participativas e menos excludentes. Corroborando as ideias de Sant´Ana (2005, p. 227):

O sucesso da intervenção do professor da sala comum depende de mudanças nas práticas pedagógicas, da adoção de novos conceitos e estratégias, adaptação ou (re)construção de currículos, uso de novas técnicas e recursos específicos para o uso com esses estudantes, novas formas de avaliação, entre outras mudanças e implementações.

Uma segunda sugestão simples de material de baixo custo são aqueles utilizados para o incremento de habilidades geométricas com ênfase na visualização de figuras espaciais. De acordo com Kaleff (2012), um grande desafio escolar é como os deficientes visuais podem ser levados a interpretar e visualizar as figuras geométricas. Nesse sentido, ainda que uma figura não esteja no campo visual de um aluno vidente, suas experiências e vivências lhe permitem buscar uma imagem mental da figura/objeto; então podemos nos perguntar: como são formadas essas imagens na mente de um deficiente visual?

Kaleff (2012) relata que experiências de estudiosos da mente e da cognição, como as apresentadas por Sternberg (2000), apontam que tanto os videntes como aqueles com DV elaboram suas imagens mentais por meio de outros sentidos, como o tato, o olfato, a audição e a percepção háptica, que é baseada em ação muscular, também chamada de tato dinâmico. Essa percepção permite a um indivíduo ser capaz de identificar dimensões e orientações de objetos pelo contato mecânico, mesmo frente a uma pequena porção de um objeto. Nesse sentido, torna-se fundamental que os alunos com DV tenham acesso a objetos e materiais adequados que possam retratar fidedignamente as figuras espaciais trabalhadas nos livros didáticos e presentes em seu cotidiano. Um exemplo desse material pode observado na Figura 10.

Figura 10: Figuras geométricas produzidas com embalagens de produtos e palitos de madeira
Fonte: Acervo do autor.

O material foi produzido por licenciandos do curso de Matemática da Universidade Federal do Estado do Rio de Janeiro que faziam estágio obrigatório de conclusão de curso no IBC em 2014, sob a orientação do autor. Foram utilizados objetos comumente encontrados em supermercados, sólidos construídos com palitos e jujubas, sólidos construídos a partir de planificações das faces e com canudos. Esses materiais possibilitam que os alunos possam identificar as relações entre vértices, arestas e faces, possibilitam ao professor trabalhar a nomenclatura dos poliedros e podem auxiliar na compreensão dos conceitos de área e volume. Kaleff (2012, p. 47) ressalta que esses materiais “ajudam a minimizar alguns obstáculos cognitivos relacionados à visualização, no momento de o aluno (deficiente visual ou não) adequar os modelos concretos de poliedros com suas representações em desenhos”. Foram utilizados materiais que pudessem representar os poliedros relacionados a dois tipos de modelos: o modelo tipo casca e o modelo tipo esqueleto, em conformidade com as ideias de Kaleff (2012, p. 47):

O modelo tipo casca de um poliedro leva à percepção do sólido como um todo, permitindo ao aluno (bem jovem, com cerca de cinco anos) se familiarizar com a forma geométrica do conceito subjacente. Por sua vez, os modelos tipo esqueleto permitem uma análise mais precisa de características relacionadas à correspondência entre pontos das arestas da estrutura concreta e a sua incidência em segmentos do desenho, entre a conservação do posicionamento das arestas (se perpendiculares, paralelas etc.) e ainda ajudam na percepção das arestas aparentes e daquelas consideradas como ocultas no desenho do sólido. A visualização de tais arestas é fundamental para o entendimento das convenções de desenho de uma representação plana do poliedro, no qual as arestas ocultas são representadas por meio de linhas pontilhadas.

O material também foi utilizado na mesma turma do 6º ano do IBC em 2014, conforme detalhado antes, e se mostrou importante para que os alunos pudessem inferir a relação de Euler de alguns poliedros regulares (mesmo sem conhecer previamente a fórmula que expressa tal relação) a partir da observação e da manipulação de seus modelos concretos.

Foi possível notar que os alunos participaram ativamente da aula, trouxeram suas experiências e relataram conhecer algumas das figuras e dos objetos utilizados na aula. Foi trabalhada a nomenclatura das figuras, a ideia de área presente nas faces e volume dos sólidos mais simples. O material mostrou-se importante para a introdução do conteúdo e possibilitou que os alunos pudessem perceber a Matemática presente em seu cotidiano sendo trabalhada em sala de aula.

Considerações finais

A experiência no trabalho com DV permite concluir que não é possível estabelecer um caminho único para tornar as aulas de Matemática acessíveis e compreensíveis aos alunos cegos e com baixa visão. No entanto, podemos concluir que existem instrumentos e ferramentas fundamentais para o trabalho com esses alunos. A correta utilização da grafia matemática em Braille para o aluno cego, a utilização de fontes e tamanhos adequados ao aluno com baixa visão, o uso do soroban e o emprego de materiais concretos e manipuláveis, sempre que possível, mostram-se imprescindíveis para que o professor possa proporcionar aulas acessíveis aos alunos incluídos. Trabalhar nesse contexto, explorando diferentes conteúdos a partir de discussões, questionamentos e material concreto, possibilita ao professor oferecer um aprendizado mais significativo, pois a aprendizagem em Matemática está ligada à compreensão, isto é, à atribuição e à apreensão de significado; apreender o significado de um objeto ou acontecimento pressupõe identificar suas relações com outros objetos e acontecimentos (Brasil, 1998).  Um conceito matemático se constrói articulado com outros conceitos, por meio de uma série de retificações e generalizações. “Assim, pode-se afirmar que o aluno constrói um campo de conceitos que toma sentido num campo de problemas, e não um conceito isolado em resposta a um problema particular” (PCN, 3º e 4º Ciclos do Fundamental, p. 41).

Os alunos devem utilizar o soroban para fazer cálculos, a grafia Braille e o CMU para fazer os registros e a formalização do conteúdo, o material adaptado/produzido pelo professor para discutir, resolver problemas, formular questões e fundamentar conceitos e definições. Com a utilização de recursos adequados, os alunos cegos e com baixa visão incluídos em turmas regulares podem vivenciar um ambiente de explorações e investigações matemáticas junto com os demais, com o propósito de descobrir alguns princípios matemáticos, padrões, regularidades e conceitos, conforme aponta Passos (2012). Ainda de acordo com a autora, é nesse ambiente que ocorre um processo, constitui-se um cenário que permite que as aulas possam ser vivenciadas por diferentes atores.

Referências

BERNARDO, F. G. Práticas pedagógicas inclusivas no ensino de Matemática para deficientes visuais e baixa visão.IV Seminário Internacional Inclusão em Educação: Universidade e Participação - Inclusão, Ética e Interculturalidade. 11-13 de maio, Universidade Federal do Rio de Janeiro, 2016.

BERNARDO, F. G. a importância do uso do soroban por alunos cegos e com baixa visão no processo de inclusão. XII Educere – Encontro Nacional de Educação. Pontifícia Universidade Católica, Curitiba, 2015. Disponível em: http://educere.bruc.com.br/arquivo/pdf2015/17122_8076.pdf. Acesso em 20 jul. 2016.

BRASIL. Lei n° 13.146/15, Lei Brasileira de Inclusão. Brasília, 2015.

BRASIL. Decreto nº 7.690, de 2 de março de 2012. Aprova a estrutura regimental e o quadro demonstrativo dos cargos em comissão e das funções gratificadas do Ministério da Educação. Brasília, 2012.

BRASIL. Ministério da Educação, Secretaria de Educação Especial. Soroban: manual de técnicas operatórias para pessoas com deficiência visual. In: Mota et al. Brasília, 2009.

BRASIL. Ministério da Educação e Cultura, Secretaria de Educação Básica. Parâmetros Curriculares Nacionais do Ensino Médio. Brasília, 2000.

BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. 5ª a 8ª séries.Brasília. 1998.

FERRONATO, R. A construção de instrumento de inclusão no Ensino da Matemática. Dissertação (Mestrado). Universidade Federal de Santa Catarina, 2002.

FIORENTINI, D.; MIORIM, M. A. Uma reflexão sobre o uso de materiais concretos e jogos no ensino de Matemática. Boletim da Sociedade Brasileira de Educação Matemática, São Paulo, SBM, ano 4, nº 7, 1990.

GLAT, R.; FERREIRA, J. R.; OLIVEIRA, E. S. G.; SENNA, L. A. Panorama nacional da educação inclusiva no Brasil. Relatório de consultoria técnica, Projeto Educação Inclusiva no Brasil. Banco Mundial, 2003.

KALEFF, A. M. Dois desafios para o ensino de Geometria e para a inclusão do deficiente visual na escola: visualização e interpretação de figuras geométricas. Revista Educação Matemática em Foco, Eduep, Campina Grande, v. 1, nº 2, ago./dez. 2012.

PASSOS, C. L. B. Materiais manipuláveis como recursos didáticos na formação de professores de Matemática. In: LORENZATO, S. (org.). Coleção Formação de professores, 3ª ed. Campinas: Autores Associados, 2012. p. 76 -92.

SANT’ANA, I. M. Educação inclusiva: concepções de professores e diretores. Psicologia em Estudo, Maringá, v. 10, nº 2, p.227-234, maio/ago., 2005.

SANTOS, M. P. Formação de professores: exercitando propostas de inclusão. Laboratório de Pesquisa, Estudos e Apoio à Participação e à Diversidade em Educação. FE-UFRJ, 2004. Disponível em: http://www.lapeade.com.br/artigos.html. Acesso em 19 jul. 2016.

STERNBERG, R. J. Psicologia Cognitiva. Porto Alegre: Artes Médicas Sul, 2000.

Leia mais sobre Inclusão e tecnologias em Educação Matemática