Estudando função afim na palma da mão

Arlen Pinheiro de Lacerda

Seeduc/RJ, PPGEduCIMAT - UFRRJ

Darling Domingos Arquieres

Seeduc/RJ, PPGEduCIMAT - UFRRJ

Felipe de Jesus Ribeiro Marques

PPGEduCIMAT - UFRRJ

Introdução

Todos os dias nos deparamos com as tecnologias digitais, como os smartphones, aparelhos celulares com funções mais avançadas, pois possuem funções semelhantes às de um computador, como acesso à internet e programas, entre outros recursos. Porém essa tecnologia é de uso proibido no recinto escolar, pela Lei nº 5.222, de 11 de abril de 2008. Entretanto, essa Lei foi modificada pela Lei nº 5.453/09, com nova redação:

Art. 1º Fica proibido o uso de telefones celulares, walkmans, diskmans, iPods, MP3, MP4, fones de ouvido e/ou bluetooth, game boy, agendas eletrônicas e máquinas fotográficas nas salas de aula, salas de bibliotecas e outros espaços de estudos, por alunos e professores na rede pública estadual de ensino, salvo com autorização do estabelecimento de ensino, para fins pedagógicos (Rio de Janeiro, 2009).

Mesmo havendo a modificação na lei, ainda existe preconceito em utilizar smartphones para fins pedagógicos, pois essa tecnologia é vista como algo que tira o foco ou desvia a atenção dos discentes das aulas. Todavia, podemos trazer esse recurso a nosso favor, utilizando em sala como recurso de aprendizagem.

Temos o objetivo de mostrar como as tecnologias digitais (TD), especificamente os smartphones, juntamente com o aplicativo escolhido, podem contribuir no aprendizado dos estudantes. Assim, analisaremos uma atividade sobre função afim.

Fundamentação teórica

Recursos digitais podem dinamizar, motivar, agilizar, instigar e facilitar o processo de ensino e aprendizagem. Contudo, vale salientar, que, apesar de “as tecnologias digitais estarem contribuindo com novas arquiteturas sociocognitivas, elas não devem ser vistas como garantia para a aprendizagem” (Bairral, 2015).

Para que o aprendizado possa acontecer, é importante que as TD sejam utilizadas em atividades investigativas, em que façam explorar novas ideias, que façam gerar descoberta(s). Assim, a partir da exploração e da(s) descoberta(s), possam gerar uma lei de formação, uma definição, isto é, uma conceitualização. Dessa maneira, acabam acontecendo dois processos de pensamento: o conjecturar e o conceituar (Bairral, 2015).

Embora existam diversos TD, escolhemos os smartphones juntamente com o aplicativo GeoGebra, pois é possível fazer download dele gratuitamente para diversos dispositivos (computadores, telefones, tablets, iPhone e iPad) e para vários sistemas operacionais. Vale também ressaltar que o GeoGebra é um software de Matemática dinâmico, que pode ser usado em todos os níveis de ensino da Matemática (Menegotto; Lara, 2011). Além disso, o programa possui excelente interface, tem fácil manejo e existe a dinâmica entre os sistemas algébricos e geométrico de representações (Resende et al., 2012). O software reúne recursos de Geometria, Álgebra, tabelas, gráficos, Estatística e Cálculo. Com interface amigável, vários recursos sofisticados e por ser de livre acesso, vem sendo utilizado em muitas pesquisas e até mesmo em sala de aula (Marques, 2014). Nessa sintonia, Soares (2012) diz:

O GeoGebra é um software para o estudo da Matemática que tem como diferencial a possibilidade de representação de objetos, como por exemplo, pontos, retas, segmentos de retas, planos, polígonos e gráficos de funções, possibilitando a fluência entre as representações tanto algébricas quanto geométricas (p. 6).

Com essa metodologia, buscamos quebrar os paradigmas educacionais e sair da nossa zona de conforto para promover produção do conhecimento humano (D’Ambrósio; Lopes, 2014). Esses autores afirmam que

o processo de produção de conhecimento humano requer atos de criatividade para o surgimento do novo, de invenções, de novas possibilidades [...] que levem ao progresso. A criatividade resulta da quebra de regras, da busca de alternativas para aquilo que já é aceito como norma e padrão. Inovações nas artes, na música, na literatura, na arquitetura surgem com a ousadia dos artistas para experimentar algo novo. Avanços científicos e tecnológicos ocorrem quando os cientistas exploram novas possibilidades, o que tem sido evidenciado nas pesquisas das áreas de Matemática, Física, Química, Medicina, Farmacologia [...]; quando eles ousam se arriscar a trabalhar fora das fronteiras estabelecidas por suas disciplinas, buscando realizar aquilo que vislumbram como novas perspectivas (p. 37).

O estudo da função de afim com o uso do GeoGebra permite que o estudante levante suas próprias indagações, suas reflexões e suas observações sobre o assunto.

Análise da atividade da função afim

A atividade aqui analisada e descrita adiante foi realizada em duas turmas do 1º ano do Ensino Médio de uma escola do município de Mesquita. Os discentes não tinham ainda estudado os conceitos desse conteúdo específico, entretanto já tinham conhecimentos anteriores sobre plano cartesiano e uma ideia geral do conceito de função. Durante a aplicação da tarefa, tivemos que nos adequar a um problema de energia na instituição; por esse motivo não pudemos utilizar o laboratório de informática e outros recursos advindos daí. Embora não imaginássemos que ocorreria tal situação, conseguimos contornar esta dificuldade, pois uma semana antes foi pedido pelo professor regente da turma que os discentes que baixassem em casa o aplicativo GeoGebra em seus smartphones.

A duração da implementação da atividade em cada turma foi de aproximadamente duas horas; os estudantes tiveram que formar grupos de três alunos (pois nem todos os alunos puderam baixar o aplicativo GeoGebra ou tinham celular); cada grupo recebeu as folhas que continham três questões abertas de cunho exploratório e investigativo:

• Questão 1. Ao variar o controle deslizante^[1] de a de acordo com o intervalo e mantendo o controle b constante (sem mexer), faça três observações e tente justificá-las.
• Questão 2. Ao variar o controle deslizante de b de acordo com o intervalo e mantendo os controles a constantes (sem mexer), faça três observações e tente justificá-las.
• Questão 3. Considere a função cujo gráfico é apresentado a seguir.

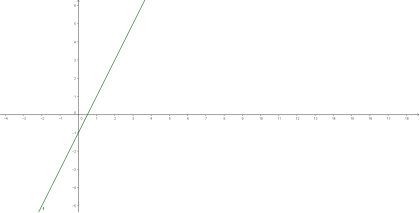
Observando o gráfico, que informações pode dizer sobre o coeficiente a e b? Tente justificar suas informações.

Antes de os estudantes iniciarem a atividade, explicamos, grupo por grupo, como montar o gráfico da função afim na forma f(x) = ax + b no GeoGebra; foram construídos dois controles deslizantes a e b, em que o controle deslizante a fazia variar o coeficiente angular e b fazia variar o coeficiente linear. O objetivo da atividade era que os alunos pudessem conjecturar a relação desses coeficientes com um gráfico da função estudada na tarefa.

Selecionamos dois trabalhos que nos chamaram a atenção, de duas turmas de 1º ano do Ensino Médio. Na análise, identificamos como grupos A e B.

Grupo A

Neste grupo, os discentes fizeram observações nas três questões. A Figura 1 ilustra a Questão 1.

Figura 1: Observações da Questão 1 do grupo A.
Fonte: Fragmento da atividade.

Na primeira observação, percebemos que o grupo estava experimentando a variação do coeficiente angular, observando possivelmente na aba algébrica do GeoGebra ou simplesmente vendo pela animação da ferramenta do controle deslizante. Na segunda observação, notamos que houve conjectura em relação do valor do coeficiente a; os estudantes relatam que, quando a = 0 e b = 0 (lembrando que a e b são coeficientes da função), o gráfico fica alinhado com o eixo das abscissas (eixo X). Entretanto, essa função não seria mais uma função afim, mas uma função constante, pois para ser função afim o coeficiente a precisar ser diferente de zero. Na terceira, os alunos descreveram de modo informal que, quando o valor do coeficiente angular for positivo (quando aumenta o valor de a), a função (a reta) fica posicionada na direita; ao contrário, quando o coeficiente angular for negativo (quando diminui o valor de a), fica posicionado na esquerda. Seguem as observações do grupo em relação à Questão 2.

Figura 2: Observações da Questão 2 do grupo A.
Fonte: Fragmento da tarefa.

Na primeira observação, o grupo menciona que tendo o coeficiente a = 0 o gráfico da função só se movimenta na vertical (para cima ou para baixo). Nesse caso, o grupo ainda não sabe que a função deixou de ser afim e passou ser constante; logo, o movimento mencionado é a mudança da constante da função. Na segunda observação, compreenderam que, quando o coeficiente a é zero, ao variar o coeficiente b se torna uma função constante e seu valor é representado no eixo Y. Na terceira observação, os discentes relataram que o valor do coeficiente b varia de -100 a 100, conforme o intervalo estabelecido no controle deslizante, e que “a linha só vai até os próprios”, ou seja, compreenderam que o valor do coeficiente b é exatamente onde o gráfico toca o eixo Y. A seguir está a resposta do grupo sobre a Questão 3.

Figura 3: Observações da Questão 3 do grupo A.
Fonte: Fragmento da tarefa.

Nesta última tarefa, possivelmente ao analisar que “a parte de baixo para a esquerda” e “a parte de cima para direita”, os discentes queriam demonstrar que, quando o coeficiente a é positivo, a função é crescente e quando a é negativo a função é decrescente.

Grupo B

Os discentes deste grupo realizaram observações nas três questões. Iniciaremos com um trecho da Questão 1 na figura a seguir.

Figura 4: Observações da Questão 1 do grupo B.
Fonte: Fragmento de atividade.

Na primeira observação, o grupo analisou que o gráfico da função gira; não percebeu em que momento há a mudança de inclinação do gráfico para determinar quando a função é crescente ou decrescente. Na segunda observação, a análise do grupo estava equivocada, pois a escrita deles coloca valores fixos para os coeficientes; logo, para essa situação não há movimento. Na terceira observação, os discentes podem ter se confundido pelo fato de a amplitude ter sido igual a 100 e possivelmente tiveram a impressão de ser uma função constante. Vale salientar que este trabalho era algo novo, tanto no conceito, quanto no uso pedagógico do smartphone em sala de aula. A seguir temos trecho da Questão 2.

Figura 5: Observações da Questão 2 do grupo B.
Fonte: Fragmento de atividade.

Na primeira observação, foi notado que o gráfico da função, quando o coeficiente a = 0 e b = 11 é paralelo ao eixo X, ou seja, é uma reta que passa pelo y = 11. Na segunda, o grupo percebeu que no gráfico da função formada há uma inclinação quando os valores dos coeficientes a = 1 e b= 21; na terceira, o grupo se equivocou, pois os coeficientes pertencem à mesma reta ou possivelmente estavam se referindo ao encontro da função com os eixos X e Y. Abaixo está a observação da Questão 3.

Figura 6: Observações da Questão 3 do grupo B.
Fonte: Fragmento de atividade.

O grupo, nesta última questão, conseguiu encontrar os valores exatos dos coeficientes; com isso, chegou à lei de formação da função afim de maneira correta. Percebemos que possivelmente o grupo, fazendo a variação dos valores de a e b no campo geométrico e vendo o campo algébrico do aplicativo, obteve sucesso em chegar à lei de formação da função. Entretanto, não podemos afirmar se esses foram seus passos.

Nesta análise, obtivemos observações interessantes dos grupos A e B, contudo sentimos falta das justificativas pedidas nas questões. Entendemos que isso possa ter acontecido por ser a primeira vez que eles trabalharam com o conceito de função afim e o programa GeoGebra. Entretanto, as atividades, juntamente com as TD, conseguiram instigar a exploração das questões, e com isso notamos que os smartphones podem ser aliados para o crescimento do seu aprendizado na sala de aula.

Considerações finais

A quebra de paradigma para a aplicação dessa aula não foi apenas no uso do smartphone, mas também o procedimento pedagógico no desenvolvimento da atividade. O GeoGebra também foi um recurso importante, pois apresenta interface de simples manuseio. Dessa forma, os alunos conseguiram visualizar e analisar a relação entre o gráfico e os coeficientes.

Nesse sentido, acreditamos que trazer tecnologias digitais para o ambiente das aulas é importante quando temos finalidades pedagógicas definidas e sem perder o direcionamento que tentamos almejar. Nas primeiras aulas, requer um pouco mais de tempo, pois tudo é novo e diferente. Nas aulas seguintes, percebemos a evolução, pois os discentes já estão se ambientado aos novos meios pedagógicos.

Não queremos que os recursos convencionais sejam esquecidos ou ignorados. Estamos trazendo uma sugestão de aula dinâmica, que pode ser incorporada às aulas de Matemática e fazer a diferença no ensino dos estudantes.

Referências

BAIRRAL, M. A. As tecnologias digitais potencializando a insubordinação criativa no currículo da formação inicial de professores de Matemática. In: D’AMBROSIO, B.S.; LOPES, C. E. (Ed.). Vertentes da subversão na produção científica em Educação Matemática. Campinas: Mercado de Letras, 2015.

D’AMBRÓSIO, B. S.; LOPES, C. E. Trajetórias profissionais de educadoras matemáticas. Campinas: Mercado de Letras, 2014 (Coleção Insubordinação Criativa).

DUVAL, R. Registros de representações semióticas e funcionamento cognitivo da compreensão em Matemática. In: MACHADO, S. D. A. (Org.). Aprendizagem em Matemática: registros de representação semiótica. Campinas: Papirus, 2003. p. 11-33.

MARQUES, F. J. R. Análise de interações de futuros professores de Matemática no ambiente VMT com GeoGebra. 2014. Monografia (Licenciatura em Matemática). Seropédica: UFRRJ, 2014.

MENEGOTTO, G.; LARA, I. C. A. Contribuições do software GeoGebra para o estudo de paralelogramos. Alexandria, v. 4, nº 2, p. 31-55, 2011.

RESENDE, W. M.; PESCO, D. U.; BORTOLOSSI, H. J. Explorando aspectos dinâmicos no ensino de funções reais com recursos do GeoGebra. 1ª Conferência Latino-Americana de GeoGebra. p. 74-89, 2012.

RIO DE JANEIRO (Estado). Lei estadual nº 5.453, de 26 de maio de 2009. Modifica a Lei nº 5.222, de 11 de abril de 2008, que dispõe sobre a proibição do uso de telefone celular nas escolas estaduais do Estado do Rio de Janeiro. Rio de Janeiro: Assembleia Legislativa do Rio de Janeiro, 2008. Disponível em: http://alerjln1.alerj.rj.gov.br/CONTLEI.NSF/e9589b9aabd9cac8032564fe0065abb4/98c0ae15f7f1a1e6832575c3005abe88?OpenDocument. Acesso em: 30 jun. 2017.

SOARES, Luís H. Tecnologia computacional no ensino da Matemática: o uso do GeoGebra no estudo de funções. In: 1ª Conferência Latino-Americana de GeoGebra. p. LXVI-LXXX, 2012. Disponível em: http://revistas.pucsp.br/index.php/IGISP/article/view/8923/6598. Acesso em 30 de jun. 2017.