Práticas matemáticas em sala de recursos multifuncional

Thaís da Silva Abdias

UERJ

Vanessa Barreto da Silva

UERJ

Jeanne Denise Bezerra de Barros

IME/UERJ/ Projeto Fundão UFRJ

Simone Pereira Monteiro

Faetec/ISERJ

Introdução

Desde a promulgação do Decreto Federal nº 6.571, em 17 de setembro de 2008, que reestrutura a Educação Especial e obriga as escolas a matricular as crianças com deficiência física ou intelectual em classes comuns do ensino regular, existe uma preocupação das instituições de ensino em como fazer a inclusão de forma exitosa. No que tange ao aprendiz surdo, deixando de lado a dificuldade maior, que é a língua materna, surge naturalmente a dificuldade primeira em Matemática e, por conseguinte, em Física e Química. O presente trabalho é a apresentação de seis atividades realizadas nos projetos de Extensão e de Iniciação à Docência, na sala de recursos multifuncional (SRM) do Instituto de Educação Governador Roberto Silveira, no município de Duque de Caxias, Rio de Janeiro, durante um semestre. Foram realizadas com os alunos da SRM de acordo com as necessidades apresentadas por cada um. Todas as atividades de matemática são elaboradas em paralelo com o aprendizado em sala de aula. Algumas atividades foram preparadas no dia da sua aplicação conjuntamente com o(s) aluno(s). Com a experiência do trabalho na SRM, constamos a importância de um apoio individualizado para esses alunos.

O estudo deste trabalho é baseado em uma SRM do Instituto de Educação Governador Roberto Silveira, localizado no município de Duque de Caxias. Encontram-se matriculados ao todo 25 alunos, sendo eles surdos, com baixa visão, deficiência intelectual e síndrome de Down, entre outros. Desses, 80% aproximadamente participam de dois projetos vinculados à UERJ, a Oficina Pedagógica de Matemática para Alunos Surdos e Discalculia em Foco: colorir para aprender. Nos dois projetos o emprego de jogos na aprendizagem de conceitos chave da Matemática é de suma importância. Como afirma Silva et al. (2014),

enquanto a criança brinca, vai garantindo a integração social, além de exercitar seu equilíbrio emocional e atividade intelectual. É na brincadeira também que se selam as parcerias, porém o aprendizado não deve estar presente só na escola, mas também como parte do dia a dia da criança; na medida em que a criança progride em seu desenvolvimento e amadurecimento, é necessário que ela manifeste o que é próprio de cada etapa de sua vida. Para as crianças, o jogo está relacionado a brincadeiras, e utilizar o jogo como instrumento do ato educativo é oferecer à criança uma aprendizagem significativa.

Os dois projetos têm como objetivo auxiliar os discentes na aprendizagem de Matemática, criando mecanismos de fixação de conceitos básicos que são necessários para o dia a dia de todo indivíduo, possibilitando a melhor visualização. O lúdico é um meio muito utilizado para a compreensão deles. A construção de materiais e revisões contínuas dos assuntos interligados à matéria dada em sala de aula são meios de inserir esses alunos cada vez mais na escola regular. Outros objetivos são a inserção do licenciando no ambiente de uma sala de recursos e o contato com diversos alunos com deficiência. Isso contribui na sua formação, fortalecendo o papel da universidade na escola básica. O discurso da necessidade de interligação dos três níveis de ensino é apontado por Speller et al. (2012, p. 142), quando dizem:

A colaboração e a complementaridade pela atuação conjunta e coordenada entre os arranjos de nível básico, médio e superior poderão desenhar um conjunto de soluções factíveis em médio prazo para dois grandes problemas da educação no país: a alfabetização e a Educação Matemática. O foco na educação e nas ciências básicas (Matemática, Física e Química) com suporte na pesquisa em temáticas de ciências humanas e sociais (Educação), a serem financiadas pelo Estado, ensejaria um diálogo cooperativo como ensino básico; faria avançar o crescimento do IDH e engendraria o suporte necessário para o esperado salto qualitativo e quantitativo em tecnologias (engenharias) de que o país carece.

Aqui acrescentamos a contribuição do saber acadêmico à escola básica, devolvendo à população um produto financiado por ela mesma (via impostos).

Metodologia

As atividades realizadas com os estudantes buscam atender aos objetivos citados; em um primeiro contato, identificamos as limitações enfrentadas pelos alunos e pesquisamos os recursos que podemos utilizar para atender às suas necessidades. O diálogo com os alunos se faz de enorme importância, pois assim podemos conhecer melhor o que agrada a eles e tentar dessa forma unir conceitos teóricos àquilo de que os alunos gostam.

Nossa busca pelo aprendizado dos alunos nos leva à construção de diferentes mecanismos de abordagem, já que cada aluno possui sua singularidade e a evolução no entendimento do conteúdo varia de acordo com diferentes fatores internos e externos ao ambiente escolar. Certas atividades levam um tempo maior para seu desenvolvimento e exigem frequência assídua do aluno para que gere bons resultados. Alguns exemplos de atividades são dados a seguir. A primeira atividade desenvolvida foi criada com o intuito de ajudar o aluno A a construir o conceito de fração e a exercitar a leitura da mesma. A atividade foi dividida em duas partes: a primeira de construção e a segunda de aplicação.
Na construção do jogo é de suma importância o aprendiz ter contato com os materiais e ele mesmo construir a atividade, pois ajuda não só na aprendizagem, mas na autoestima do estudante, como é o caso do aluno em questão, em que é visível sua baixa autoestima.

Corrida de frações

Público-alvo: 6º ano do Ensino Fundamental
Duração: 1 aula de 50minutos, no máximo.
Objetivo: Introduzir o conceito de fração e desenvolver uma leitura de frações.
Construção do material da atividade: Produziu-se um dado com os números de 1 a 6 para serem os numeradores e outro dado com os números de 2 a 7 para serem os denominadores. Tiras de papel cartão em tamanhos iguais, divididas em 2, 3, 4, 5, 6 e 7 pedaços (Figura 1).
Na aplicação, cada aluno, na sua vez, joga os dois dados e observa o número da face voltada para cima e escreverá a fração obtida com o lançamento dos dados. Por exemplo, se ele obtiver o número 2 no dado dos numeradores e o número 5 no dado dos denominadores, ele formará a fração. Então ele pegará a fita que está dividida em cinco partes e andará com seu carro 2 partes. As jogadas acontecem até que um aluno chegue em primeiro lugar à faixa de chegada.

O estudante mostrou-se confuso para identificar o denominador e o numerador, na leitura das frações, porém percebeu que fração é uma divisão, conseguindo fazer perfeitamente as divisões das tiras. No decorrer do jogo, percebeu-se um entusiasmo do aluno, pois conseguiu fazer as marcações corretamente.

Figura1: Corrida de frações.

A segunda atividade foi desenvolvida por Barreto e Abdias para auxiliar o aluno B em suas dificuldades no conteúdo sobre ângulos e sua baixa estima, que prejudica diretamente o seu rendimento em sala de aula. Essas percepções foram observadas durante a execução dos exercícios voltados ao tema mencionado anteriormente.

Relógio dos ângulos
Público-alvo: 7º ano do Ensino Fundamental
Duração: 1 aula de 50 minutos, no máximo.
Objetivo: Classificação dos ângulos conforme suas medidas em agudos, retos, obtusos e rasos.
Construção do material da atividade: uso de papel cartão, canetas coloridas, régua e transferidor para montar o relógio e realizar a atividade (Figura 2).

Na tentativa de facilitar a compreensão do conteúdo, foi criado de forma ilustrativa um relógio analógico com a finalidade de exemplificar as classificações das medidas dos ângulos. O relógio foi confeccionado pelo próprio aluno, que foi informado de que uma volta completa corresponderia a 360°, no caso dos ponteiros das horas e dos minutos apontados no mesmo ponto (número). A partir dessa informação, o aluno foi questionado sobre algumas situações de horários; nesse caso ele respondia qual ângulo representava tal comportamento dos ponteiros. Posteriormente, o estudante era informado da classificação formada pelo ângulo. A atividade foi realizada por dois alunos. Sob orientação, os dois alunos foram muito bem. Esse resultado se deve a três razões: número reduzido de alunos realizando as atividades, maior atenção dada pelas bolsistas dos projetos e tempo livre para realização da atividade.

Figura 2: Relógio dos ângulos. À esquerda, a construção da atividade pelo aluno B; à direita, o relógio no término da atividade.

A terceira atividade foi desenvolvida por Barreto e Abdias com quase todos os alunos atendidos nos dois projetos. É uma atividade básica para os alunos da SRM pela dificuldade que eles têm com multiplicação. O tempo de aprendizagem desses alunos é diferente do tempo de um aluno que não tem necessidades especiais.

Muitos alunos têm dificuldades para realizar cálculos rápidos; sendo assim, pudemos observar que para auxiliar em expressões numéricas ou em atividades que necessitam de cálculos maiores, a tabuada de 1 até 10 é uma base que ajuda em desenvolvimentos mais rápidos e o aluno ganha mais tempo para outras atividades.

Tabuada individual de multiplicação
Público-alvo: a partir do 2º ano do Ensino Fundamental e Ensino Médio
Duração: 2 aulas de 50 minutos, dependendo da turma. Objetivo: Construir uma tabuada individual.
Construção do material da atividade: uso de papel cartão – nove retângulos (um para cada tabuada, a partir da multiplicação por 2), canetas coloridas, régua.
Para que a autonomia dos alunos cresça cada vez mais, cada um faz seu próprio material de estudo (Figura 3). O ritmo para desenvolvimento da tabuada da multiplicação varia de acordo com a limitação de cada um. Para o desenvolvimento da atividade utilizamos papel cartão cortado em tamanhos iguais e cada aluno faz a sua tabuada com canetas coloridas ou lápis coloridos. As cores também ajudam no interesse do aluno pela atividade, segundo o projeto de Discalculia.

Figura 3: Tabuada individual de multiplicação – Aluno B construindo sua tabuada de multiplicação.

A quarta atividade foi criada com o intuito de auxiliar um aluno com DI a associar número a seus pares, o aluno C, que tem problemas cognitivos que prejudicam a memorização e dificultam o aprendizado. O dominó foi construído em papel cartão e o aluno finalizou colorindo os algarismos. A princípio a atividade foi feita para que o aluno ligasse algarismo-algarismo, mas pode ser adaptada para ligar algarismo-escrita por extenso ou algarismo-quantidade.

Dominó numérico
Público-alvo: alunos com DI.
Duração: 1 aula de 50 minutos.
Objetivo: Associar os números visualmente.
Construção do material da atividade: Construir o dominó em papel cartão pelas estagiárias do projeto sem cor. Parte de colorir deixada para o aluno (Figura 4).

A atividade, além de ajudar no reconhecimento dos números, também trabalha a coordenação motora do aluno, que pode ser suporte para outras tarefas. Além de o aluno se sentir parte do processo construtivo, ele é motivado a participar mais ativamente das aulas.

Figura 4: Dominó numérico –Aluno C colorindo o dominó.

Um aluno de 8º ano tem grande dificuldade em atividades que trabalham os principais ângulos, que são 90º, 180º, 270º e 360º. Para auxiliar o aluno no ambiente externo à sala de recursos, desenvolvemos a quinta atividade, construindo esses ângulos em cores distintas em cartolina e unindo com fitilho para que possa prender no caderno ou estojo.

Principais ângulos
Público-alvo: 6º ano do Ensino Fundamental.
Duração: 1 aula de 50 minutos.
Objetivo: Identificar e associar ângulos às situações rotineiras.
Construção do material da atividade: uso de folhas coloridas A4,canetas coloridas, transferidor e fitilho de uma cor. Superpor 1 disco, ¾ do disco, ½ e ¼ coloridos, furados no centro e presos com fitilho (Figura 5).

Foram apresentados ao aluno D os ângulos no quadro-negro. A informação foi assimilada pelo aluno. Em seguida, os mesmos ângulos foram mostrados no disco da Figura 5, quando foi realizado algum progresso na aprendizagem desses quatro ângulos.

O mesmo trabalho pode ser feito em papéis de gramaturas distintas para criar a visão 3D, que expande o recurso para alunos com deficiência visual. Pensar em atividades que possam ser modificadas e adaptadas a outras realidades é fundamental para que os trabalhos tenham alcance maior.

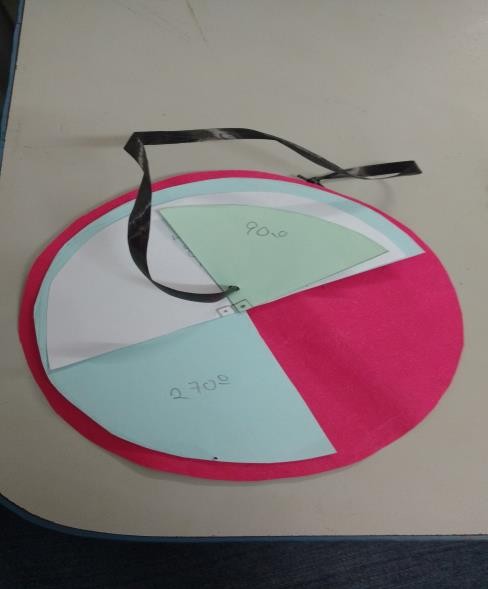
Figura 5: Principais ângulos.

Por último, semanalmente os estudantes surdos que cursam o 1° ano do Ensino Médio trazem atividades propostas pelo professor de Matemática da classe regular, listas de exercícios, questões do livro didático ou no próprio caderno do aluno e a partir disso eles são assessorados para a realização.

Listas de exercícios
Público-alvo: alunos surdos do Ensino Médio (primeiro ano).
Duração: semanalmente.
Objetivo: Auxiliar na aprendizagem da matéria na classe regular.

Na tentativa de compreensão dos tópicos dados em sala de aula e trazidos pelos alunos em forma de listas de exercícios do professor de Matemática, foram adotados alguns passos para facilitar o aprendizado dos estudantes. Primeiramente, busca-se identificar o nível de absorção dos conteúdos ministrados em sala de aula, em seguida relembrar as matérias básicas que serão necessárias para a realização das atividades. Posteriormente, procura-se resolver exercícios parecidos com os da lista, explicando passo a passo. Por último, os aprendizes realizam a atividade e expõem o que foi assimilado.

Além das dificuldades no conteúdo programado de Matemática, os alunos surdos nas classes regulares se deparam com aulas em Língua Portuguesa, sua segunda língua,com a falta de intérprete, professores desqualificados para trabalhar com alunos deficientes e material didático que não abrange a todos. Nesse contexto, o apoio das estagiárias em formação na universidade tem peso significativo no processo de aprendizagem desses alunos.

Considerações finais

Os resultados obtidos estão diretamente relacionados com a frequência do aluno na SRM e a organização deles, pois o processo de aprendizagem requer etapas, e pausá-las, na maioria das vezes, prejudica o aprendiz. Sobre a organização escolar, a maioria dos participantes do projeto não tem mostrado esse hábito, como copiar a matéria toda e de maneira disposta, porém esses mesmos alunos estão desenvolvendo agora.

A realidade dos alunos socialmente reflete seu desempenho em sala de aula. Acompanhar essa realidade também é crucial para ajudá-los da melhor forma. A abordagem adotada varia de acordo com diferentes fatores que podem facilitar o contato aluno-professor ou até dificultar esse trabalho. Amparar o estudante em relação ao que é vivenciado na sala regular é uma das etapas necessárias para o desenvolvimento dele.

A participação desses alunos nas feiras culturais que ocorrem no colégio se faz de extrema importância, pois a SRM também ajuda na socialização do aluno, além de melhorar a autoestima dos aprendizes. Nesses eventos, todos veem a forma de trabalho implementada na SRM e que é algo que beneficia e auxilia os estudantes que antes eram segregados pelo sistema de ensino tradicional.

Por fim, os trabalhos aplicados na sala de recursos podem ser facilmente expandidos para as salas regulares.

Referências

COUTINHO, M. D. M. C. A construção de saberes num contexto de educação bilíngue para surdos em aulas de Matemática numa perspectiva de letramento. Tese de doutorado, Unicamp, 2015.

SILVA, A. A.; SANTOS, D. R. N.; COSTA, E. K. B. A importância do jogo na aprendizagem da Matemática e na Educação Infantil. Disponível em: http://www.omep.org.br/artigos_ver/986/a-importancia-do-jogo-na-aprendizagem-da-matematica-e-na-educacao-infantil.

SPELLER, P.; ROBL, F.; MENGHEL, S. M. Desafios e perspectivas da Educação Superior brasileira para a próxima década: 2011-2020. Unesco, 2012. Disponível em: http://unesdoc.unesco.org/images/0021/002189/218964POR.pdf.

Leia mais sobre Inclusão e tecnologias em Educação Matemática