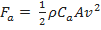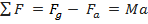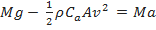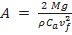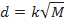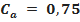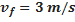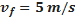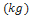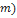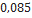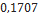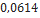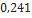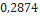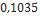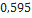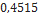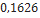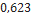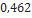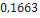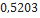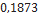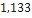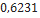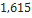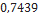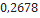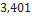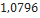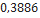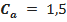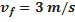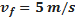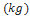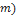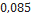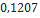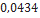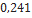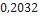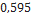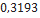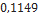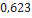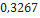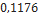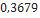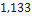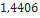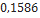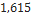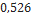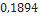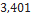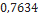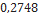Paraquedas, funções e computadores: por que não programar?

André Luiz Cordeiro dos Santos

Professor adjunto do Departamento de Matemática (Cefet/RJ)

Alexandre de Souza Soares

Professor associado do Departamento de Matemática (Cefet/RJ)

Pedro Ferraz Villela

Professor adjunto do Departamento de Matemática (Cefet/RJ)

Paraquedas: breve histórico

O primeiro relato escrito sobre o conceito de paraquedas foi encontrado nos cadernos de Da Vinci, na época do Renascentismo italiano. O desenho retratava um tecido bem preso a uma estrutura piramidal rígida. Embora Da Vinci nunca tenha feito esse dispositivo, ele recebe crédito pelo conceito de levar o homem à terra com segurança usando um desacelerador de arrasto máximo.

Fauste Veranzio construiu um dispositivo semelhante àquele encontrado no desenho de Da Vinci e saltou de uma torre em Veneza em 1617. Mais de um século se passaria antes que novos desenvolvimentos fossem feitos pelos irmãos Montgolfier. Em 1783, eles realizaram saltos de paraquedas com animais a partir de telhados ou balões. Nesse mesmo ano, Sebastian Lenormand saltou de uma torre usando um paraquedas de 4,32m de diâmetro. O primeiro uso emergencial de paraquedas foi feito por Blanchard em 1785, após o balão de ar quente em que ele estava explodir. Blanchard também desenvolveu um paraquedas de seda dobrável, pois até então todos os paraquedas eram construídos com um quadro rígido.
Em 1797, Garnerin fez o primeiro salto com um paraquedas sem armação rígida. Ele saltou de um balão a 2.440m de altura, altitude muito relevante à época, tendo sido observado por um astrônomo francês, Lalandes. Durante a descida, o paraquedas sofreu fortes oscilações induzidas no velame. Com base nisso, Lalandes sugeriu fazer um pequeno orifício perto do ápice da cúpula do velame, o que diminuiu drasticamente as oscilações nessa parte da estrutura do paraquedas.

Com o advento do avião, houve um interesse renovado pelo paraquedas. Em 1912, o capitão do exército norte-americano Albert Berry foi a primeira pessoa a saltar de paraquedas de um avião. Desde a Primeira Guerra Mundial até o início dos anos 1930, os paraquedas de seda redondos convencionais permaneceram inalterados em suas estruturas. Eles foram usados ​​principalmente por militares na Europa, na Rússia e nos Estados Unidos. Durante a década de 1930, Kurt Student concebeu e implementou uma força de ataque possibilitando que homens, equipamentos e armas saltassem de paraquedas de planadores e aeronaves. Nessa época, a Alemanha demonstrou a eficácia das tropas aéreas entregues no campo de batalha usando paraquedas.

Os paraquedas modernos, desenvolvidos para altas velocidades e altas altitudes, têm início de desenvolvimento nos anos 1930. Knacke e Madelung projetaram um paraquedas para desacelerar cargas pesadas de alta velocidade. Após a Segunda Guerra Mundial, Knacke inventou o paraquedas anelar, que é usado para velocidades subsônicas moderadas. Esse paraquedas é usado principalmente para entrega de carga e desaceleração de aeronaves.

Como funciona o paraquedas?

O princípio básico de funcionamento de um paraquedas é aumentar a área de um objeto em queda, criando um sistema com grande área em contato com o ar, diminuindo com isso a velocidade de retorno do objeto ao solo. Do ponto de vista físico, há dois elementos fundamentais que compõem esse cenário: a força de gravidade e a força de arrasto. A força de arrasto, devida à resistência do ar, faz resistência ao movimento descendente do objeto, isto é, a força de arrasto opõe-se à direção da velocidade.

Um cálculo preciso da força de arrasto é um tanto complicado e não existe uma “lei geral” que possa ser utilizada em todas as situações em que haja resistência gerada pelo ar. Entretanto, uma boa estimativa da magnitude da força de arrasto devida à resistência do ar, aqui denotada por 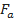, agindo sobre o sistema objeto-paraquedas, pode ser dada por

em que 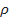 representa a densidade do ar (unidade: 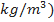,  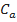representa o coeficiente de arrasto (é uma grandeza adimensional),  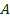representa a área exposta do velame do paraquedas (unidad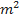e: ) e 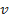 representa a velocidade descendente do objeto (unidade: ).

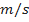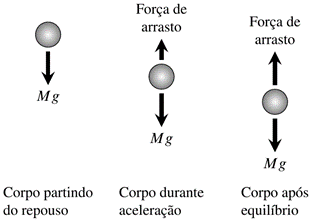
Figura 2: Diagrama de forças agindo sobre o objeto durante a queda

A equação (1) mostra que, quando o objeto inicia o movimento de descida, após atingir o apogeu, a força de arrasto pode ser negligenciada, já que a velocidade nesse momento é pequena. Por outro lado, à medida que a velocidade do objeto é maior, a força de arrasto passa a ser significativa. Considerando-se o movimento ao longo da direção vertical e assumindo a aceleração da gravidade positiva para um corpo em queda, a Segunda Lei de Newton assegura que:

Dessa forma,

onde 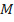 representa a massa total do sistema objeto-paraquedas,  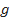é a aceleração da gravidade e  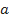é a aceleração resultante do sistema. Em algum momento, a força de arrasto será (aproximadamente) igual ao peso do sistema objeto-paraquedas. Assim, a aceleração resultante é quase nula, de modo que a velocidade final  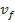será atingida e (praticamente) constante.

Quão grande deve ser o paraquedas?

A área da seção transversal do velame do paraquedas, em função da velocidade final, é dada por:

Figura 3: O velame é a parte superior, na cor cinza
Fonte: Estes Rocket Factory.

Daqui em diante, admite-se que o velame do paraquedas tem seção transversal circular de diâmetro 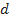. Uma vez escolhida a velocidade final adequada para o retorno do objeto ao solo em segurança, o diâmetro  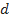passa a ser função exclusivamente da massa  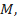pois todos os outros parâmetros são conhecidos. Assim, tem-se

com
.

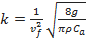É natural pensar que melhores resultados serão obtidos ao se construir um paraquedas com área muito grande. De fato, a equação (4) enseja que, quanto menor for a velocidade final desejada, maior deverá ser a área do velame a ser utilizado. Entretanto, há dois inconvenientes imediatos na prática dessa ideia. O primeiro se deve ao fato de que há limitações de espaço no compartimento destinado a alojar o paraquedas. Já o segundo é proveniente do fato de que, quanto maior for a área do paraquedas e quanto mais tempo o objeto estiver no ar em queda, maior é a possibilidade de o vento empurrar o objeto para longe de onde se deseja pousar.

Assim, idealmente, o paraquedas deve ter tamanho adequado para que o objeto tenha um pouso suave e, ao mesmo tempo, retorne ao solo num tempo razoável.

Cálculo do diâmetro: minifoguetes

O foguetemodelismo é a prática de projetar, construir e lançar minifoguetes. São modelos geralmente de pequena escala que utilizam uma plataforma de lançamento e acessórios tais como sistema de disparo e motores a pólvora negra. Geralmente são recuperados por meio de paraquedas, dentre outros modos de recuperação. Apesar de o hobby de lançar minifoguetes existir desde o início do século XX, sua prática se popularizou fortemente somente após o lançamento do primeiro satélite artificial (o Sputnik 1) pela União Soviética em 1957. A partir daí, o tema espacial virou uma verdadeira febre, incentivando principalmente os jovens a praticar o foguetemodelismo. Na mesma época, nos Estados Unidos, era fundada a empresa Estes de foguetemodelismo, que, pela primeira vez, produziu minifoguetes em grande escala e com segurança, além de kits e uma série de acessórios necessários para a prática.

Quando se deseja utilizar o paraquedas como método de recuperação do foguete, é possível utilizar as fórmulas apresentadas antes para determinar o tamanho que o paraquedas deve ter em função dos parâmetros do foguete e do próprio paraquedas e da velocidade final que se deseja. Essa é uma boa aplicação que ilustra o uso do conceito matemático de função – a obtenção de um valor final (diâmetro do paraquedas) que corresponderá aos parâmetros desejados. Outra questão relacionada é como efetivamente calcular o valor da função em termos dos parâmetros; para isso, o computador pode ser de grande ajuda, como veremos adiante.

Nesta seção, utilizando dados de modelos de minifoguetes comercializados, serão apresentados os resultados do cálculo do diâmetro dos velames de paraquedas do sistema de recuperação. Esses resultados são obtidos em função da massa do foguete, pois a velocidade final é fixada normalmente, definida de 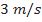 a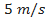. No que se segue, será assumido que 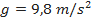, , 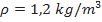 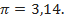Além disso, os velames considerados são de dois tipos: planos ou em forma de cúpula (hemisfério).

Tabela 1

Tabela 2

Discussão: qual o papel do computador?

Ao observar as Tabelas 1 e 2, nota-se que o cálculo dos valores da expressão do diâmetro (isto é, 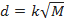) não é trivialmente realizado. É hora de apelar ao computador! O professor terá a oportunidade de alertar os estudantes sobre como o computador pode ser útil em situações reais e artificiais como as normalmente apresentadas nos textos. Qualquer software gratuito, imediatamente acessível a professores e alunos, poderá, por meio de programação elementar, fornecer muito rapidamente os resultados das tabelas. Um dos softwares mais populares e fáceis de utilizar é o GeoGebra; entre diversas outras aplicações, ele pode ser usado para o cálculo de funções que o usuário determina via fórmulas matemáticas.

Como ilustração, construímos no próprio GeoGebra uma interface que permite imediatamente determinar o diâmetro de um paraquedas em função dos demais parâmetros, utilizando o que foi visto antes. Disponibilizamos essa interface publicamente em um website encontrado aqui.

No website, o usuário pode informar a massa do sistema foguete-paraquedas, a velocidade final de recuperação, a densidade do ar e a geometria do velame do paraquedas (plano ou hemisférico); o programa exibirá automaticamente o diâmetro que o paraquedas deverá ter para os parâmetros apresentados.

Em geral, é desejável que seja encorajado que o aluno use o computador para esse tipo de aplicação, uma vez que ele permite ao aluno a livre e rápida experimentação com diferentes e interessantes conceitos matemáticos. Enfim, postulamos que os primeiros passos em programação elementar possam ser dados no Ensino Médio. Por que não?

Referências

LUCAS, J. The Silken Canopy: history of the Parachute. Airlife, 1997.

NICHOLAS, J.G. College Physics: reasoning and relationships. Brooks/Cole, 2010.

GeoGebra. Disponível em: https://www.geogebra.org.