Ideia intuitiva de limite usando o círculo e a circunferência

Este trabalho apresenta o resultado de uma atividade proposta na disciplina Análise, do Programa do Pós-Graduação em Ensino de Matemática da UFRJ. Tal atividade consistiu em elaborar e realizar uma aula sobre algum conteúdo matemático cujas ideias advenham da Análise, de maneira problematizada. Optamos por abordar a noção intuitiva de limite através da área do círculo em uma turma do segundo ano do Ensino Médio de um colégio estadual situado no subúrbio do Rio de Janeiro.

Para descrever nossa trajetória, faremos uma reflexão inicial sobre os saberes docentes, a fim de suscitar a importância de compreender a complexidade do trabalho do professor e focar no conhecimento de conteúdo e horizonte como peça importante nessa profissão. Em seguida, apresentamos a escolha do tema, a metodologia do trabalho e os processos de coleta e análise, além do plano de aula. Por fim, apresentamos um relato de experiência de como a aula ocorreu na prática e discutimos os registros escritos dos alunos coletados para tecer as considerações finais.

Algumas aproximações com a teoria

O que o professor precisa saber para ensinar Matemática de maneira problematizada? Aqui, entendemos o termo “problematizada” no sentido um ensino de Matemática que seja discutido e questionado pelos professores entre si e com seus alunos, ao invés de simplesmente ministrar aulas tradicionais com definição, exemplos e exercícios, com a justificativa de que é sempre ensinado assim. Problematizar não implica apenas questionar o formato da aula, mas sim sua mediação, conteúdos, currículo escolar etc., considerando o conhecimento prévio dos educandos.

Para discutir a Matemática escolar, cremos que não basta simplesmente que os professores saibam essa matemática. Será que para ensinar a área do círculo basta saber que ele vale πr²? Acreditamos que não, que é necessário saber mais do que os conteúdos da escola: é preciso conhecer a Matemática escolar de um ponto de vista superior (Klein, 2010), além de lançar mão de outros saberes que possibilitem que o professor tenha boas práticas que favoreçam a aprendizagem.

Nesse sentido, é sabido que vem crescendo o número de trabalhos sobre os saberes docentes no campo da Educação Matemática. Baseados, em sua maioria, no trabalho pioneiro de Shulman (1986), eles tentam refinar, compreender e testar empiricamente os saberes inicialmente discutidos. Esse foi o autor que introduziu a noção do Conhecimento Pedagógico do Conteúdo como um amálgama entre o Conhecimento do Conteúdo e o Conhecimento Pedagógico.

Dentre esses trabalhos, podemos destacar os estudos de Deborah Ball e seus colaboradores, que propuseram um refinamento para a categorização inicial de Shulman (1986) no campo da Matemática, baseado na prática. Ball, Thames e Phelps (2008) discerniram empiricamente seis subdomínios dentro dessas categorias: Conhecimento Comum do Conteúdo (CCK), Conhecimento Especializado do Conteúdo (SCK), Conhecimento de Horizonte (HCK), Conhecimento do Conteúdo e dos Alunos (KCS), Conhecimento do Conteúdo e do Ensino (KCT) e Conhecimento do Conteúdo e do Currículo (KCC). Nessa perspectiva, os três primeiros estariam contidos no Conhecimento (disciplinar) do Conteúdo e os três últimos no Saber Pedagógico do Conteúdo (Figura 1).

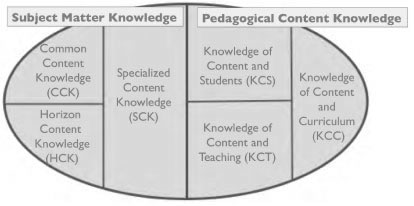
Figura 1: Conhecimento matemático para o ensino e seus subdomínios
Fonte: Ball, Thames e Phelps (2008, p. 403).

O Conhecimento Comum de Conteúdo (CCK) é o que tanto os professores de Matemática quanto os não professores devem conhecer ao acertar uma questão, enquanto o Conhecimento Especializado (SCK) é único para o ensino (p. 399-400). Ele foi a principal contribuição de Ball et al. (2008), e perpassa tarefas específicas do professor que ensina Matemática, envolvendo uma descompactação do que é necessário para o ensino, como escolher um exemplo que representa melhor determinado conceito, escolher o melhor registro semiótico para ensinar um objeto, questionar os alunos com a finalidade de chegar a uma conclusão sobre um problema etc.

O Conhecimento de Horizonte, partindo da definição de Ball e Bass (2009), é um tipo de visão periférica da Matemática com vistas ao ensino, uma visão panorâmica para além do que a prática requer.

O Conhecimento do Conteúdo e dos Alunos (KCS) é a interseção entre o conhecimento da Matemática e os conhecimentos acerca do aluno, permitindo ao professor antecipar ideias prováveis, corrigindo, intervindo e dando-lhes autonomia. O Conhecimento do Conteúdo e do Ensino (KCT) aborda a relação entre Matemática e ensino, diferenciando tarefas/problemas introdutórios de tarefas/problemas avançados, mensurando qual atividade é mais fácil ou mais difícil em termos gerais etc. Por fim, o Conhecimento do Conteúdo e do Currículo (CCK) versa sobre a diversidade de materiais didáticos disponíveis e de programas existentes e implica conhecer um conjunto de características que facilita ou dificulta a aprendizagem na prática.

Apesar de parecer estruturalista, a grande contribuição de Ball e seus colaboradores foi compreender como a profissão professor (de Matemática) é uma tarefa complexa, e desde então tem-se (re)pensado a formação inicial e continuada dos professores na perspectiva dessa pluralidade de saberes.

Voltando um pouco no tempo e na ideia da Matemática necessária ao trabalho do professor, mesmo tendo preocupação com a disciplina como ciência, Klein (2010) defendia que docentes deveriam olhar para a Matemática escolar “de cima”. Mesmo sendo de época muito anterior a Shulman, Klein indica ter impressões semelhantes sobre o saber necessário para o ensino, como enfatizam Rangel, Giraldo e Maculan (2014):

Klein entende que o professor deve não somente ter conhecimentos específicos sobre os conceitos e as teorias que ensina, mas também saber relacioná-los e articulá-los, compreender sua natureza científica e sua evolução histórica, de forma a desenvolver uma visão ampla o suficiente para situá-los no panorama da Matemática como ciência (Rangel; Giraldo; Maculan, 2014, p. 2, grifo nosso).

Neste trecho, destacamos a palavra “panorama” pois aparece na definição de Ball e Bass (2009) para o HCK. Especificamente, em nosso contexto de uma disciplina de Análise Real, tivemos contato com conceitos mais refinados dos conjuntos numéricos, limites, sequências, séries etc. que nos possibilitaram uma visão “de cima” de alguns conteúdos da escola e, como eles se articulavam com os da disciplina, dando uma ideia mais panorâmica da Matemática. Vale ressaltar que as aulas eram conduzidas pelo professor Victor Giraldo com vistas ao ensino e de forma problematizada, ou seja, a todo momento discutíamos conexões dos conteúdos vistos com a Matemática escolar. Os registros escritos e gravados da aula do professor Victor Giraldo encontram-se no canal do grupo de Pesquisa LaPraME no YouTube.

Assim, ao ministrar uma aula sobre círculo usando a ideia intuitiva de limite de forma problematizada, mobilizamos diversos dos saberes mencionados acima, mas o HCK em especial, pois exigia conectar e situar o conteúdo e validar argumentos dos alunos, dentre outros.

Para situar melhor o leitor, a definição mais refinada do HCK sugere que ele é:

uma orientação para familiaridade com a(s) disciplina(s) que contribui(em) para o ensino escolar, provendo os professores com um senso de como o conteúdo ensinado está situado e conectado com o território mais amplo da disciplina. O HCK inclui conhecimento explícito dos caminhos e ferramentas para o conhecimento da disciplina, os tipos de conhecimento e suas garantias, e de onde as ideias se originam e como suas verdades ou validades são estabelecidas. HCK também inclui consciência das orientações e valores disciplinares fundamentais e das estruturas principais da disciplina. HCK habilita os professores a ouvir os alunos, a julgar a importância de ideias ou questões particulares e a tratar a disciplina integralmente, todos os recursos que equilibram as tarefas fundamentais de conectar os estudantes a um vasto e desenvolvido campo (Jakobsen et al., 2013, s.p., tradução nossa).

Assim, com base na definição e evidenciando esse conhecimento em específico, vamos descrever o planejamento da aula sobre a noção de limite usando a ideia da área do círculo, além de discutir sua aplicação e seus resultados.

Justificativa

Nas discussões da disciplina Análise cursada por nós, o professor Victor Giraldo ressalta continuamente a necessidade da problematização do ensino de Matemática, uma vez que o ensino desconexo com essa prática pode, e tem levado, ao ensino de uma Matemática meramente procedimental.

Mas o que é problematizar? Na visão do professor Victor, problematizar é uma postura a ser adotada pelo professor que ensina Matemática, uma vez que dentro desse paradigma é importante repensar e levar para os estudantes uma reflexão acerca das estruturas do objeto matemático que está sendo ensinado; é discutir que quando estruturas mudam também as propriedades e os conceitos a serem estudados mudam. Ou seja, não basta ensinar que não é possível fazer a subtração de um número menor por um maior no conjunto dos números naturais como algo posto, mas sim discutir os “porquês” e os “comos” de isso acontecer, já antecipando ideias do contato com os números inteiros (Giraldo, 2017).

O objetivo da aula, em uma turma do 2º ano do Ensino Médio em uma escola estadual do subúrbio do Rio de Janeiro, foi alcançar a noção intuitiva de limite para compreender a fórmula da área do círculo; utilizou-se uma abordagem problematizada e contraintuitiva que valoriza os conhecimentos prévios dos educandos mediante recursos de vídeo, material concreto e discussões.

Para atender ao objetivo principal, foi necessário atingir alguns objetivos específicos e intermediários, como: apresentar a noção de infinito, que é algo contraintuitivo, apresentar o método de exaustão, construir a fórmula da área da circunferência com o método e subsidiar a ideia intuitiva de limite.

Metodologia

Para o planejamento do trabalho nos reunimos via internet e elaboramos, entre idas e vindas de numerosos e-mails, um plano de aula para aplicação. Ao iniciar a escolha por um tema/atividades para a aula, quisemos ir além dos livros didáticos tradicionais e propostas de sites e blogs. Assim, começamos a buscar nos livros de Cálculo alguma questão que pudesse ser discutida com alunos do 2º ano no Ensino Médio. O tema surgiu após a leitura de uma apostila de Cabral (2010) da UFRJ, em que uma questão sobre a fórmula da área do círculo nos intrigou. Apesar de não ser um conteúdo do Ensino Médio, ele está na Educação Básica e optamos por apresentá-lo utilizando conhecimentos matemáticos mais refinados, de modo compreender o porquê de sua fórmula e problematizar algumas ideias por trás da sua construção, como o Método da Exaustão e a ideia de limite de maneira intuitiva.

Esta pesquisa é de natureza qualitativa, que é a mais adequada para abordar fenômenos das ciências humanas, pois

proporciona a possibilidade de vislumbrar o objeto/sujeito de pesquisa de vários modos, e o que permite que isso aconteça são as diversas técnicas de coleta empregadas. Os métodos utilizados na pesquisa qualitativa contribuem para uma coleta de dados ampla e permitem apreender o caráter complexo e multidimensional dos fenômenos em sua manifestação natural (André, 1983, p. 66).

Assim, durante a aplicação do plano de aula, a professora regente da turma utilizou diversos métodos de coleta, como produções orais dos estudantes em diário de campo e dos registros escritos deles, além de registros fotográficos de suas intervenções no quadro.

Optamos por apresentar o planejamento inicial da atividade que descrevemos abaixo e depois um relato de como a aula ocorreu na prática, além de analisar o porquê das modificações; por fim, faremos uma análise da produção escrita dos alunos, separada por categorias.

Para a coleta de dados foi realizado um planejamento didático, acompanhado do tempo para duração de cada etapa, apenas para efeito de organização (Quadro 1).

Quadro 1: O plano de aula inicial

O relato de experiência

Uma vez que uma das autoras deste relato é professora regente de Matemática em um colégio estadual da Cidade do Rio de Janeiro localizado em Pedra de Guaratiba, onde leciona para duas turmas do 2º ano médio técnico integrado em Telecomunicações, ela se prontificou a aplicá-lo, a anotar em um diário de campo as considerações referentes à aplicação e a recolher as produções textuais dos alunos participantes face às atividades propostas.

Na prática, alguns ajustes foram necessários durante a aula. Apresentamos aqui o relato da aplicação da atividade, as modificações feitas e suas justificativas. Para isso, a partir deste momento, a professora Daniela narra em primeira pessoa do singular, destacando entre aspas e em itálico as falas dos alunos registradas em seu diário de campo, os acontecimentos da aplicação, que ocorreu no dia 6 de novembro de 2017, no laboratório de Matemática e Física da escola e da qual participaram 27 alunos de uma das turmas. A turma foi escolhida por ser mais participativa e facilitar a discussão. A dinâmica da aplicação se dividiu entre debate para todas as atividades propostas, exceto a atividade final, que contou com respostas individuais por escrito.

A aula

Iniciei a aplicação do plano de aula propondo a primeira atividade prevista; para isso, perguntei aos alunos: O que é área? Recebi as seguintes manifestações:

— Espaço em que algo está inserido.

— Área infinita, área esférica, um infinito esférico, pois parece não ter início nem fim.

— Um cone infinito?

Enquanto os alunos respondiam, eu incentivava que mais estudantes expusessem suas observações. É importante salientar que busquei não emitir juízo de valor sobre as respostas apresentadas, não obstante os estudantes que as emitiram estivessem sempre me questionando se estavam certos ou errados após as suas falas. Observei que a busca pelo “gabarito” da atividade proposta estava no centro das preocupações dos alunos, o que indica que para eles somente seriam propostas perguntas que tivessem uma solução única e conhecida pela professora.

Quando as manifestações dos alunos quanto à primeira questão cessaram, propus a segunda provocação prevista: Como calculamos a área da circunferência? Por que calcular assim? Imediatamente após a pergunta, a turma começou a falar simultaneamente de círculos e circunferências, confundindo os dois objetos. Nesse momento senti necessidade de ir ao quadro para explicar a diferença entre círculo e circunferência, indicando que o primeiro está associado à ideia de área e o segundo, à ideia de perímetro. Entretanto, durante a minha intervenção os estudantes se lembraram da constante π e perguntaram qual era a sua relação com a circunferência, ou seja, associaram a constante à ideia de circunferência, mas não souberam precisar qual era tal relação.

Para responder aos alunos, fui além da relação entre perímetro e circunferência e área e círculo apresentada no alto do quadro e mostrei a constante π como valor imutável associado à divisão do perímetro da circunferência pelo seu diâmetro; mencionei que tal fato valia para quaisquer tamanhos de circunferência, como se pode observar na Figura 2.

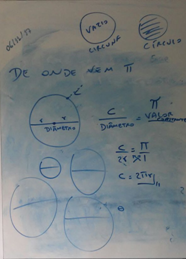
Figura 2:  Círculo, circunferência e π
Fonte: Autoras.

Após minha intervenção, a turma iniciou um burburinho em que brotaram aos borbotões as seguintes afirmações em relação ao cálculo da área da circunferência:

— Usando raio, 360°, PI, diâmetro, 2 πr, π radianos...

— Não se calcula se não tem nada, calcular o quê...

Uma aluna argumentou que “bastava tirar a circunferência, esticar um barbante e medir...”. Perguntei a ela como seria possível calcular a área dessa forma, ao que ela respondeu: “Sei lá, multiplica por 2”. Essa resposta aleatória indica a desistência do caminho tomado por ela na discussão da temática e a ideia de que uma operação matemática de multiplicação está associada à ideia de área. Após essa breve interlocução, os estudantes continuaram a emitir suas opiniões sobre o assunto:

— Não faz nada, pois é espaço vazio...

— Mas a borda alguma área tem...

— Calcula com π, pois π é infinito...

— Se você tem um balde com nada é nada...

— Para calcular a área do círculo usamos raio radianos, diâmetro, grau, a fórmula πr²...

Após intenso debate, a turma estava muito confusa e vários alunos colocavam enfaticamente seus pontos de vista, que se contrapunham e que eram defendidos veementemente por quem os enunciava. Mais uma vez me abstive de fazer qualquer juízo de valor sobre as colocações dos alunos, me limitando a estimular a fala e o debate, não obstante fosse constantemente chamada a fazê-lo pelos alunos que queriam que eu validasse seus pontos de vista, uma vez que a ideia de que existia uma resposta correta e única e que eu era a detentora dessa resposta permanecia forte nas concepções dos participantes.

Com a curiosidade dos alunos aguçada pelas dúvidas que só se avolumavam conforme a aula avançava, compreendi que seria interessante modificar o planejamento original, trazendo para o segundo momento da aula, em lugar do Paradoxo de Zenão, o vídeo Quanto vale a área do círculo (Open University, 2017), que estava inicialmente previsto como terceira atividade do dia (Figura 3).

Figura 3: Quanto vale a área do círculo?
Fonte: Autoras.

Os alunos se surpreenderam com o vídeo, que apresenta o cálculo da área do círculo como o desenrolar de infinitas circunferências que vão diminuindo até o raio zero (Figura 4) e que perfazem a figura de um triângulo retângulo de base 2^πr e altura πr, o que leva à conhecida fórmula para a área do círculo A = πr².

Figura 4: Contínuo de circunferências
Fonte: Matemática Rio (2017).

Durante e após a exibição do vídeo, os alunos ficaram se perguntando como poderiam existir infinitas circunferências se o vídeo indicava finitas circunferências e, afinal de contas, o que era infinito?

Alguns deles não compreenderam o cálculo da área do círculo com a apresentação e discussão do vídeo. Na aula original havia a previsão, com o objetivo de apresentar outra abordagem para o tema, do uso de um vídeo em que se apresenta um círculo “infinitamente” fatiado cujos pedaços são arranjados de forma a criar um retângulo de base πr e altura r, o que também leva à conhecida fórmula para a área do círculo A = πr². Entretanto, como a aula foi aplicada em um laboratório de Matemática e dentro dele tínhamos à mão um modelo concreto da ideia apresentada no vídeo em questão, optei por substituir o vídeo pelo uso do material concreto (Figura 5). Durante o uso do material argumentei que o retângulo só seria perfeito se cortássemos infinitas fatias do círculo.

Figura 5: Círculo fatiado e setores reagrupados em forma de retângulo
Fonte: Autoras.

Para lidar com a questão do infinito, expliquei à turma que, se o vídeo se propusesse a apresentar infinitas circunferências ou que se tentássemos cortar as infinitas fatias de que o círculo precisaria ser composto, certamente nunca terminaríamos nem de assistir ao vídeo nem de cortar fatias. Para ilustrar minha fala sobre infinito, inseri na aula o vídeo O Hotel de Hilbert (Figura 6), (Unicamp, 2017), pois já o tinha na minha galeria de vídeos, uma vez que ele me foi apresentado nas aulas de Análise.

Figura 6: Trecho do vídeo O Hotel de Hilbert
Fonte: Unicamp (2017)

O vídeo em questão apresenta o paradoxo dos infinitos, por meio de uma metáfora criada pelo matemático alemão David Hilbert. O paradoxo do Hotel de Hilbert

é um experimento mental matemático sobre conjuntos infinitos apresentado pelo matemático alemão David Hilbert (1862-1943). É chamado de paradoxo pois o resultado é contraintuitivo. Considere um hotel hipotético com infinitos quartos, todos ocupados – isto é, todos os quartos contêm um hóspede. Suponha que um novo hóspede chega e gostaria de se acomodar no hotel. Se o hotel tivesse apenas um número finito de quartos, então é claro que o pedido não poderia ser cumprido, mas como o hotel possui um número infinito de quartos então se movermos o hóspede do quarto 1 para o quarto 2, o hóspede do quarto 2 para o quarto 3 e assim por diante (simultaneamente), movendo o hóspede do quarto N para o quarto N+1, podemos acomodar o novo hóspede no quarto 1, que agora está vago. Por um argumento análogo é possível alocar um número infinito (contável) de novos clientes: apenas mova o hóspede do quarto 1 para o quarto 2, o hóspede do quarto 2 para o quarto 4, e em geral do quarto N para o quarto 2N; assim todos os quartos de número ímpar estarão livres para os novos hóspedes (Wikipedia, 2017, p. 1).

Vale destacar que David Hilbert nasceu em 23 de janeiro de 1862 e morreu em 14 de fevereiro de 1943. Foi um matemático alemão cujo trabalho em Geometria teve a maior influência no campo desde Euclides. Depois de fazer um estudo sistemático dos axiomas da Geometria Euclidiana, Hilbert propôs um conjunto de 21 axiomas e analisou o significado deles (Somatematica, 2017, s.p.). Logo no início da exibição do vídeo, quando, mesmo com o hotel lotado, é possível acomodar mais um hóspede sem desalojar ninguém, os alunos entraram “em pânico” e falaram que:

— O último hospede foi para o quarto da faxineira!

— Esse último hóspede foi jogado na rua, pois não era possível acomodar mais ninguém!

— Se estava lotado, para entrar alguém, teria que sair alguém!

Notei que alguns alunos se exaltaram bastante na defesa das considerações. Essa postura se intensificou ao longo da exibição do vídeo, que apresenta na sequência um ônibus com infinitos hóspedes sendo acomodados. E culminou em uma inconformação geral na ação seguinte à da acomodação do ônibus com infinitos hóspedes, que foi a acomodação de infinitos ônibus com infinitos hóspedes. Os alunos ficaram tão alterados que parei o vídeo nesse ponto para permitir que eles extravasassem a sua indignação. Reproduzo as suas falas:

— Mas como está lotado se é infinito?

— A vida não é assim!!!

Aqui fica evidente que os alunos acreditam que a contextualização na Matemática, “rainha das ciências”, deve ocorrer exatamente como na vida real, não permitindo ampliar certos pensamentos e acreditar em algo contraintuitivo. Apesar de muitos verem em filmes americanos super-heróis que voam, o que também não representa a realidade, é aceitável pelo fato de ser recreação e fora de um contexto educativo.

Um aluno me perguntou diretamente: por que não botar as pessoas para o final?  Respondi que não seria possível, pois o hotel estava cheio! Em seguida a essa minha resposta, outras falas dos alunos se seguiram, desta vez se alternando entre a negação e a aceitação das ideias apresentadas, indicando como o conceito de infinito é difícil de ser aprendido rapidamente, e requer amadurecimento. Reproduzo-as na sequência:

— Isso é de doente!

— Tô quase pegando...

— O prédio vai cair!

Uma aluna perguntou: “Quantos andares tem o prédio?”, ao que eu respondi: “infinitos!” Após essa resposta, a turma entrou em discussão negando e ponderando as possibilidades de infinitos quartos, hospedes e ônibus; os alunos entraram em “parafuso” ao mesmo tempo!

Após a exibição e discussão desse vídeo, apresentei aos alunos o Paradoxo de Zenão, com Aquiles e a Tartaruga (Figura 7) (Open University, 2017) para discussão dos infinitésimos, uma vez que no item anterior discutimos infinitas circunferências e infinitas fatias. Aqui o objetivo foi indicar que a espessura das circunferências ou das fatias pode ser tão fina quanto se queira, ou seja, o conceito de limite foi abordado intuitivamente.

Figura 7: Trecho do vídeo O paradoxo de Zenão
Fonte: Open University (2017).

A reação dos estudantes ao vídeo foi de aquiescência à ideia de que algo pode ir diminuindo e diminuindo e nunca ser zero. O que pode explicar essa aquiescência é que, como no 2º ano eles já tiveram contato com o comportamento assintótico de funções exponenciais de base fracionária que tendem a zero, a ideia não é estranha a eles. Além disso, tiveram também o estudo de progressão geometria de razão entre 0 e 1 e o cálculo de sua soma, o que vai ao encontro do fato que Aquiles completa o percurso.

Como, durante a aula, a discussão dos infinitos se mostrou urgente, não tivemos tempo de fazer a construção informal do conceito de área do círculo com a exploração da construção do GeoGebra prevista no plano original. Eu apenas disse aos alunos que a construção existia e que seria disponibilizada a eles pelo e-mail da turma.

Para finalizar a aula, propus, como atividade individual, as perguntas finais previamente elaboradas: 1) Na fórmula da área do círculo estamos incluindo a circunferência ou não? 2) Em caso negativo, a área é a mesma após a retirada de um círculo. Agora vamos tirando todas as circunferências do círculo, uma de cada vez. Ao final, teremos retirado tudo; a área é zero? 3) Em caso afirmativo, qual a área da circunferência sem o círculo? Pense e escreva sobre isso.

Enquanto elaboravam respostas a esses questionamentos, os alunos pediram para ver o vídeo dos círculos contínuos novamente. Também mais uma vez a confusão entre circunferência e círculo se estabeleceu e tive que lembrá-los de que a circunferência é “vazia por dentro”, o que não ocorre com o círculo. Os estudantes perguntaram como seria possível responder às três perguntas propostas, uma vez que as duas últimas pareciam se excluir; como resposta a esses questionamentos, encorajei-os a reler as questões e a procurar respondê-las de acordo com o seu entendimento.

Procedimentos de análise dos registros dos alunos

Para a análise do material coletado, fizemos a redução dos dados por meio do agrupamento das produções escritas dos estudantes por semelhança, disparidade ou complementaridade para cada uma das três perguntas propostas. Utilizamos o diário de campo junto aos registros escritos no quadro, a fim de triangular as informações fornecidas pelos alunos, no intuito de dar mais clareza à nossa análise.

Foram analisados os registros de 27 alunos. A seguir, apresentamos as principais respostas e, quando necessário para discussão, agrupamos em categorias de acordo com similaridades e disparidades, visto que não foram identificadas complementaridades.

Em relação à questão 1) Na fórmula da área do círculo estamos incluindo a circunferência ou não?, 23 alunos responderam que sim e quatro responderam que não, o que pode indicar que alguns ainda permaneceram confusos quanto ao fato de o círculo ser a região delimitada por circunferência, ou seja, não se atentaram à impossibilidade de existir um círculo sem circunferência. Apesar de a professora ter feito a distinção entre os dois elementos geométricos, como descrito no diário de campo, propositalmente não foi feita essa observação na aula, de que não seria possível um círculo sem circunferência a fim de não influenciar as respostas individuais.

No 3º ano, quando em Geometria Analítica se estuda a equação da circunferência, o círculo será visto como a região cuja distância é menor ou igual a um ponto fixo, o que inclui a circunferência. Assim, alguns alunos consideraram o círculo apenas como a região interior, um conjunto aberto na topologia, e na verdade seria o fecho desse conjunto, ou seja, o interior somado à sua fronteira. O interior é o conjunto dos pontos interiores de um conjunto A. Um conjunto aberto é aquele que só possui pontos interiores. A fronteira é o conjunto dos pontos tais que em qualquer bola centrada neles de raio ε existem pontos do conjunto A e pontos do complementar de A. O fecho do conjunto é a união do seu interior com a sua fronteira (Giraldo, 2017). Para o professor dar o feedback a esse aluno, precisa recorrer a conceitos mais refinados de Topologia e apresentá-lo de maneira didática e problematizada, fazendo uso do HCK. Logo, tal fato corrobora nossa ideia de que o professor de Matemática saber calcular a área do círculo não o prepara para responder a esse tipo de dúvida.

A partir da primeira questão, dividimos os alunos em dois grandes grupos para análise: os que responderam “não” e os que responderam “sim”. O grupo do “não” prosseguiu para o item 2: “No caso negativo, a área é a mesma após a retirada de um círculo. Agora vamos tirando todas as circunferências do círculo, uma de cada vez. Ao final, teremos retirado tudo e a área é zero”.

Nesse grupo, os quatro alunos concordaram com o que está proposto no enunciado, e a área da circunferência sem o círculo seria zero, o que pode ser indicado pelo trecho abaixo, retirado do registro do aluno A (Figura 8).

Figura 8: Resposta do aluno A
Fonte: Autoras

Os quatro alunos tiveram ideias similares, de que mesmo havendo infinitas circunferências dentro do círculo, à medida que são retiradas estamos retirando “bordas” de espessura mínima (circunferências) e esse processo repetido infinitas vezes chega a zero. Aqui, nos parece que eles compreendem a ideia de que pode existir um limite zero em uma sequência decrescente, ou seja, de um número real que representa área total sendo retirados infinitésimos resultaria em zero. Porém, no início da aula a professora disse que a circunferência não possui área, e sim comprimento. Ou seja, esse grupo teve dificuldades em assimilar a ideia de que não faz sentido falar de área de circunferência, e atribuíram um valor ínfimo a essa “área”, chegando ao resultado zero.

Inferimos que talvez esses alunos tenham sido influenciados pelo primeiro vídeo da demonstração de área do círculo, em que ele tem várias circunferências internas desenroladas e reagrupadas de maneira a formar um triângulo. Assim, de acordo com o vídeo, o círculo seria um conjunto de infinitas circunferências.

No segundo grupo, os 23 alunos que responderam sim prosseguiram ao item 3: “No caso afirmativo, qual a área da circunferência sem o círculo? Pense e escreva um pouco sobre isso”. Devido à pluralidade de justificativas, dividimos as respostas em categorias, de acordo com similaridades e disparidades. Não foi identificada complementaridade nas respostas.

Dentro da categoria: “Não é possível calcular a área”, sete alunos responderam que não é possível calcular a área da circunferência sem o círculo, pois estará vazia, o que pode ser ilustrado pela fala do aluno B (Figura 9).

Figura 9: Resposta do aluno B: “Não tem como, pois o cálculo está vazio, não tem números para cálculo, impossível calcular a área da circunferência sem o círculo”
Fonte: Autoras

Diferente do primeiro grupo (grupo do “não”), aqui os alunos parecem entender o conceito de círculo como região delimitada pela circunferência, e que não faz sentido falar em área de circunferência, e sim em comprimento. Logo, a fórmula da área não seria aplicada, até mesmo porque qual seria o comprimento do raio nesse caso?

Na categoria: “Área igual a 2πr”, doze alunos responderam que é possível calcular a área da circunferência sem o círculo, e a mesma vale 2πr, o que pode ser ilustrado pela fala do aluno C (Figura 10):

Figura 10: Resposta do aluno C
Fonte: Autoras

Este grupo, que representou a maioria dentro dos que responderam “Sim”, foi de difícil inferência. Após discussões, optamos por descrever possíveis entendimentos, tendo em vista que há mais dúvidas do que certezas de nossa parte.

Pelo exposto, parece que compreenderam o conceito de que a área do círculo inclui a circunferência, pois responderam sim à questão 1. Porém associaram a fórmula do comprimento da circunferência à área. Isso pode ter ocorrido por conta do vídeo apresentado com a demonstração da área do círculo, e os alunos podem ter entendido que sem o círculo não há infinitas circunferências dentro, apenas uma, a de fora, e que ao desenrolar restaria apenas um segmento de comprimento 2πr, que seria a base do triângulo.

Aqui, percebemos que, às vezes, um recurso didático, que normalmente é visto como um facilitador da aprendizagem, mesmo com objetivos bem definidos a serem alcançados, pode na verdade conduzir a ideias incorretas, funcionando de maneira contrária ao esperado.

Todas as disparidades ocorreram com os alunos que responderam sim: um aluno afirmou que é possível calcular a área da circunferência sem o círculo e que ela é 2πr². Pelo fato de o aluno não ter justificado tal resposta, não identificamos se ele confundiu uma das fórmulas (círculo ou circunferência) ou escreveu uma delas (a área ou o comprimento) de maneira incorreta.

Outro aluno respondeu que não conseguiu pensar na justificativa, podendo indicar que o permaneceu sem ação e confuso diante da questão, o que pode ter sido ocasionado pelo fato de que tais conceitos não são simples de assimilar, principalmente em apenas uma aula. É importante ressaltar que na escola básica normalmente não se discutem tais ideias, e o aluno não está acostumado a refletir, pode estar mais familiarizado com respostas fechadas e outros tipos de propostas.

Houve ainda um aluno respondeu que não é possível encontrar um valor, pois é infinito. Aqui não identificamos se o aluno quis dizer que a área da circunferência ou do círculo é infinita. Em ambos os casos, ele pode não ter compreendido a delimitação da figura ou não compreendeu o conceito de limite. Ele também pode ter pensado que, tirando a circunferência, a região se espalhou e o círculo ficou aberto e sem limitação, tendo área infinita.

Considerações finais

O presente relato teve como proposta apresentar a noção intuitiva de limite para compreender a área do círculo, amparada na noção de infinito e no método de exaustão. Ao longo do trabalho buscou-se uma abordagem problematizada, diferente do convencional, uma vez que a proposta incluiu o uso de vídeos, material concreto e reconhecer os conhecimentos dos alunos, fomentando debates para compreender as ideias, para além do foco nos procedimentos.

É importante destacar que a atividade foi realizada dentro do tempo proposto no planejamento e houve algumas alterações no momento de aplicação, com a intenção de atender às demandas que foram surgindo com o tempo disponível.

Sabemos que os conceitos abordados demandam tempo de amadurecimento, indo além de uma aula. Assim, não pretendemos com esta proposta de atividade que os alunos tenham compreendido e interiorizado muitos conceitos abordados, mas serviu para despertá-los para uma visão problematizada da Matemática, além de abrir precedentes para outras discussões afins. É certo que os alunos da turma que cursarem uma graduação na área de Exatas já chegarão à universidade mais familiarizados com esses conceitos, necessários a disciplinas como Cálculo Diferencial e Integral, por exemplo.

Consideramos também que o vídeo da demonstração da área do círculo com o desenrolar de circunferências formando um triângulo pode ter confundido algumas ideias, e nos parece melhor utilizar somente o de método de exaustão em uma primeira aula, funcionado aqui como uma sugestão para possíveis futuras atividades. Talvez com os conceitos mais sedimentados o vídeo poderia ser utilizado.

Essa proposta foi inesperada, saindo no planejamento diário da disciplina da professora regente, colocando-nos fora de zona de conforto no planejamento e execução, uma vez que demandou de todos, mas especialmente da professora Daniela, que aplicou a atividade, muitos saberes docentes, em especial SCK e HCK. Tal fato ficou evidente no diário de campo, pois durante as falas da professora percebe-se que a todo momento ela reposicionou etapas e deu feedback aos alunos; para tanto ela precisou conhecer ideias da Análise, fazendo uso da visão panorâmica descrita no HCK e da Matemática problematizada. Isso confirmou que, para ensinar Matemática escolar, não basta apenas saber o conteúdo da escola básica, mas conteúdos mais avançados e estratégias de ensino (outros saberes docentes).

Com base na experiência, deixamos também algumas sugestões que podem dar continuidade ao tema. É interessante apresentar também a construção informal do conceito de área do círculo com a exploração da construção do software GeoGebra. Para tanto, localizamos um material com esse fim (Machado, 2017). É possível acrescentar, em vídeo, uma ideia intuitiva do Método da Exaustão para a área do círculo (Mathematics Online, 2017), seguido de algumas perguntas disparadoras para o debate da ideia de limite usando o círculo: É possível haver a subdivisão de algo em infinitas partes? Uma pizza por exemplo? Seria possível termos uma pizza infinita?

Para não concluir, esta foi uma atividade que nos agradou muito, pois deu mais sentido ao curso da Análise ao possibilitar uma conexão com a nossa prática. Esperamos ter mais experiências como esta e que mais professores possam trabalhar a Matemática de maneira problematizada, olhando para a Matemática elementar de um ponto de vista superior.

Referências

ANDRÉ, Marli Eliza A. Texto, contexto e significados: algumas questões na análise de dados qualitativos. Cadernos de Pesquisa, São Paulo, nº 45, p. 66-71, maio 1983.

BALL, D. L.; THAMES, M. H. T.; PHELPS, G. Content Knowledge for Teaching, What Makes It Special? Journal of Teacher Education, p. 389-407, 2008.

CABRAL, M. A. P. Curso de cálculo de uma variável (Apostila). Rio de Janeiro: Instituto de Matemática, 2010.

JAKOBSEN, A.; THAMES, M. H.; RIBEIRO, C. M. Delineating issues related to horizon content knowledge for mathematics teaching. In: Proceedings of the Eight Congress of the European Society for Research in Mathematics Education, p. 3.124-3.125, 2013.

KLEIN, F. Matemática elementar de um ponto de vista superior. Vol. 1, 1ª parte: Aritmética. Trad. Tiago Pedro e Suzana Metello de Nápoles. Lisboa: Sociedade Portuguesa de Matemática, 2010.

MATHEMATICS ONLINE. Circle Area (Demonstration). Disponível em: https://www.youtube.com/watch?v=YokKp3pwVFc. Acesso em 06 nov. 2017.

MACHADO, L. A área do círculo pelo Método da Exaustão. GeoGebra Tube. Disponível em: https://www.geogebra.org/m/Jqm3GReT. Acesso em 3 nov. 2017.

MATEMÁTICA RIO. Demonstração da área do círculo. Disponível em: https://www.youtube.com/watch?v=rxtSp45nFDw. Acesso em 06 nov. 2017.

OPEN UNIVERSITY. 60 segundos de aventura no pensamento – Aquiles e a tartaruga (Paradoxo de Zenão). Disponível em: https://www.youtube.com/watch?v=0NOHEY2ZJCg. Acesso em 06 nov. 2017.

RANGEL, L. G.; GIRALDO, V.; MACULAN, N. Matemática Elementar e Saber Pedagógico de Conteúdo – Estabelecendo Relações. Professor de Matemática Online – SBM, nº 1, v. 2, 2014.

SHULMAN, L. S. Those who understand. Knowledge Growth in Teaching, Palo Alto, v. 15, p. 4-14, 1986.

SOMATEMATICA. David Hilbert. Disponível em http://www.somatematica.com.br/biograf/hilbert.php. Acesso em: 07 nov. 2017.

UNICAMP. O Hotel de Hilbert. Disponível em: https://www.youtube.com/watch?v=pjOVHzy_DVU. Acesso em 06 nov. 2017.

WIKIPEDIA. O paradoxo do Hotel de Hilbert. Disponível em: https://pt.wikipedia.org/wiki/Hotel_de_Hilbert. Acesso em: 10 nov. 2017.