O ambiente competitivo e a construção do conhecimento de frações no sexto ano

A educação no Brasil é um direito de todos e dever do Estado. Tem sua garantia estabelecida na Constituição Federal de 1998 e deve ser ofertada com qualidade em estabelecimentos de ensino que apresentem boas condições de funcionamento, com pessoal qualificado e estrutura pedagógica que permita o aprendizado dos discentes envolvidos no processo.

Políticas públicas e pesquisas que tenham como objetivo proporcionar a melhoria na qualidade do ensino público ofertado são essenciais para transformar a realidade educacional brasileira. Discutir a qualidade na educação significa debater variáveis que interferem no processo de aprendizagem, como concentração de renda, desigualdade social e o direito à educação. Essa discussão não pode deixar de lado as questões envolvendo sistemas e unidades escolares, condições de trabalho, processos de gestão escolar, currículo, formação dos professores e elementos ambientais de ensino dentro da sala de aula que norteiam a construção do conhecimento dos discentes.

Ou seja, oferecer ensino com qualidade é um desafio que depende da dinâmica pedagógica, dos fatores econômicos, sociais, culturais e políticos de uma dada sociedade. Dourado, Oliveira e Santos (2007) afirmam que a qualidade da educação é um fenômeno complexo, abrangente, que envolve múltiplas dimensões, não podendo ser apreendido apenas por um reconhecimento da variedade e das quantidades mínimas de insumos indispensáveis ao desenvolvimento do processo de ensino-aprendizagem; muito menos, sem tais insumos. Em outros termos, a qualidade da educação envolve dimensões extra e intraescolares e, nessa ótica, deve-se considerar os diferentes atores, a dinâmica pedagógica, ou seja, os processos de ensino e aprendizagem, os currículos, as expectativas de aprendizagem e os diferentes fatores extraescolares que interferem direta ou indiretamente nos resultados educativos.

Portanto, é inegável que a melhoria na qualidade do ensino está relacionada ao conhecimento que o discente adquire em sua jornada na escola. Conhecimento que, segundo Driscoll (1994), é o resultado das experiências individuais com o mundo, sendo construído pelos aprendizes quando eles resolvem problemas, por meio da interação do indivíduo com o meio social e físico, dependendo tanto das condições do meio quanto das condições do indivíduo.

Ainda nessa linha de raciocínio, pode-se citar Piaget, que afirma que o conhecimento é dinâmico e depende da interação entre o sujeito e o meio no qual ele está inserido (Piaget, 2011). O sujeito busca equilíbrio entre as necessidades internas com as novas situações a fim de garantir sua adaptação. Isso implica que, para entender o processo de aprendizagem, é indispensável observar as relações que o sujeito estabelece com o meio e como o meio influencia esse processo (Piaget, 1986). O presente trabalho procura verificar a influência de um ambiente competitivo na qualidade da construção do conhecimento de discentes do 6º ano do Ensino Fundamental para o conteúdo de frações.

Competição

Competição humana é um evento em que duas ou mais pessoas lutam por um objetivo que não pode ser compartilhado, geralmente resultando em um vencedor e um perdedor. Indivíduos e/ou grupos estão, então, em uma posição em que eles devem disputar a realização de um resultado. Por exemplo, na maioria das competições esportivas em equipe, estas se envolvem com o propósito de ganhar jogos para tirar o primeiro lugar em um torneio (Freire; Scaglia, 2003).

É controverso se a concorrência na Educação é positiva. Por exemplo, Verhoeff é um forte defensor de seus benefícios, alegando que uma competição bem organizada desafia seus participantes a fazer o melhor possível; portanto, aumenta a motivação e a aprendizagem dos alunos (Verhoeff, 1997). Lawrence concorda com essa ideia dizendo que a concorrência estimula a aprendizagem ativa e aumenta a motivação (Lawrence, 2004). Por sua vez, Fulu também reconhece várias chances em competições, como ganho de reconhecimento e maior motivação e autoestima (Fulu, 2007). Além disso, um elemento competitivo pode funcionar como incentivo para que todos os alunos coloquem mais esforço e os alunos ainda mais fracos persistam com a participação na atividade (Fasli; Michalakopoulos, 2005), sem contar que geralmente existe alto senso de competição entre os estudantes (Siddiqui; Khan; Akhtar, 2008).

No entanto, evidências indicam que os danos da concorrência no processo de aprendizagem ocorrem ao forçar os alunos a se concentrar em objetivos, em vez de no próprio processo (Lam et al., 2001), além de que o estresse a que um estudante envolvido em uma competição é exposto tem efeito negativo, sendo ainda maior do que os benefícios extraídos a partir dele (Vockell, 2004).
Apesar da existência da discussão se a competição em sala de aula ser saudável ou não, o que é claro é que há recursos que uma atividade competitiva deve ter a fim de torná-la mais benéfica – ou pelo menos não prejudicial (Shindler, 2007; Thousand; Villa; Nevin, 1994; Yu et al., 2002).

Cantador e Conde (2010) e Shindler (2007) elencam alguns dos recursos relacionados à definição de uma concorrência saudável. Em primeiro lugar, os prêmios para os vencedores devem ser simbólicos ou de muito pouca importância, a fim de garantir que os esforços dos alunos são específicos e não impulsionados pelo prêmio obtido. Em segundo lugar, a competição deve ser curta. Uma competição longa aumenta seu senso de destaque e diminui o sentido de intensidade e diversão, ambos efeitos indesejáveis. Por outro lado, a competição tem que ser longa o suficiente para evitar a desmotivação do estudante por causa de maus resultados iniciais e para garantir que todos os participantes tenham boa chance de ganhar até o final da atividade. Finalmente, o objetivo da competição deve ser claramente definido para o processo em vez de nos resultados, deixando claro que ganhar ou perder tem baixa importância em comparação com a aprendizagem e as melhoras que acontecem enquanto competem.

Programa Institucional de Bolsa de Iniciação à Docência (Pibid)

O Pibid tem como uma de suas propostas a contribuição para a formação do professor com o estímulo à docência dos licenciandos das diferentes áreas do conhecimento. Cada instituição formadora de professores participante do Pibid desenvolve ações visando atender a essa proposta geral do programa (Capes, 2009). É um programa que propõe estreitar a relação da formação inicial nas universidades – nos cursos de licenciatura – com a prática profissional dos professores nas escolas, incorporando nos licenciados elementos que contribuirão para a formação de sua identidade profissional docente.

Essa iteração na escola ocorre pela convivência dos graduandos com o cotidiano do exercício da função docente, em condições estimulantes, criativas e diversificadas. Com isso, o programa pretende estimular a permanência dos bolsistas na docência, contribuindo, assim, para ajustar essas ofertas às demandas das nossas redes públicas, minimizando as carências de professores da Educação Básica.

Dentre os objetivos do Pibid está a elevação da qualidade das ações acadêmicas voltadas à formação inicial de professores nos cursos de licenciatura das instituições de Educação Superior, assim como a inserção dos licenciandos no cotidiano de escolas da rede pública de educação, promovendo a integração entre Educação Superior e Educação Básica (Capes, 2009).

O programa visa proporcionar aos futuros professores participação em experiências metodológicas, tecnológicas e práticas docentes de caráter inovador e interdisciplinar e que busquem a superação de problemas identificados no processo de ensino-aprendizagem, levando em consideração o Ideb e o desempenho da escola em avaliações nacionais, como Provinha Brasil, Prova Brasil, Saeb e Enem, entre outras.

Além dos aspectos listados sobre o programa, destaca-se que o exercício da docência insere-se na prática social e tem papel fundamental na formação humana. Constrói-se a partir da autonomia e do conhecimento especializado, manifestado em competência e capacidade para desempenhar o trabalho com compromisso, responsabilidade e profissionalismo (Capes, 2009). Perrenoud (1999) assevera que a profissionalização se amplia quando cede espaço a estratégias orientadas por objetivos e por ética. Afinal, saber onde está, aonde se quer chegar e qual caminho tomar a favor da aprendizagem é compromisso da parceria entre professor e estudante.

Sexto ano do Ensino Fundamental

Segundo os Parâmetros Curriculares Nacionais - PCN (Brasil, 1998) o Ensino Fundamental compõe, juntamente com a Educação Infantil e o Ensino Médio, o que a Lei nº 9.394/96 (a Lei de Diretrizes e Bases da Educação Nacional – LDB) nomeia como Educação Básica e que tem por finalidade desenvolver o educando, assegurar-lhe a formação indispensável para o exercício da cidadania e fornecer-lhe meios para progredir no trabalho e em estudos posteriores.

A LDB indica que o objetivo da formação básica é desenvolver a capacidade de aprender, tendo como meios básicos o pleno domínio da leitura, da escrita e do cálculo, a compreensão do ambiente natural e social, do sistema político, da tecnologia, das artes e dos valores em que se fundamenta a sociedade, o desenvolvimento da capacidade de aprendizagem, tendo em vista a aquisição de conhecimento, habilidades e a formação de atitudes e valores. Finalmente, a promoção do fortalecimento dos vínculos de família, dos laços de solidariedade humana e de tolerância recíproca em que se assenta a vida social (Brasil, 1996).

Para a área de Matemática, os PCN (Brasil, 1997) constituem um referencial para a construção de uma prática que favoreça o acesso ao conhecimento matemático que possibilite de fato a inserção dos alunos como cidadãos no mundo do trabalho, das relações sociais e da cultura. Os Parâmetros destacam que a Matemática está presente na vida de todas as pessoas, em situações em que é preciso, por exemplo, quantificar, calcular, localizar um objeto no espaço, ler gráficos e mapas, fazer previsões; mostram que é fundamental superar a aprendizagem centrada em procedimentos mecânicos, indicando a resolução de problemas como ponto de partida da atividade matemática a ser desenvolvida em sala de aula.

A Matemática também faz parte da vida das pessoas como criação humana, ao mostrar que ela tem sido desenvolvida para dar respostas às necessidades e preocupações de diferentes culturas, em diferentes momentos históricos; aqui leva-se em conta a importância de incorporar ao seu ensino os recursos das tecnologias da comunicação (Brasil, 1997).

De acordo com o novo Programa de Matemática do Ensino Básico, o estudo das frações deve iniciar-se logo no primeiro ciclo, como uma relação parte-todo, representando partes numéricas, números menores que a unidade ou que foi dividida em partes iguais. Essa precocidade na apresentação das frações possibilita ao aluno um contato mais prolongado com esses números ao longo da sua escolaridade (Brasil, 1997).

Procura-se desde cedo promover o desenvolvimento do sentido de número, incluindo nele também as frações. Torna-se então relevante proporcionar ao aluno oportunidade e tempo para construir um bom conceito de fração, na medida em que as frações são essenciais para o posterior desenvolvimento de outros conceitos matemáticos. Mais ainda: Kieren (1976) argumenta que as frações constituem um fundamento para as relações algébricas posteriores e que sua compreensão é essencial para o desenvolvimento de ideias matemáticas.

Se a resposta não é uma quantidade inteira de objetos, então ela vai ser dada, correta ou muito aproximadamente, por um número fracionário. O foco principal é tornar clara para a criança a existência de situações significativas do contexto que demandam a introdução de novos números. Números têm que funcionar na vida, não só em figuras divididas, em que nem adquirem verdadeiramente esse significado (Bertoni, 2009).

Os PCN (Brasil, 1997) para o ensino da Matemática no segundo ciclo dos anos iniciais consideram o ensino das frações como fundamental para a aprendizagem dos números racionais. Para a construção do conceito de número racional, enfatizam sua utilização em diferentes situações do cotidiano. Nesse ciclo, os alunos devem ter contato com situações problema cujas soluções não estejam no campo dos números naturais, possibilitando a aproximação destes ao conceito de número racional. Os PCN afirmam, ainda, que a representação decimal é percebida no cotidiano com mais frequência do que a forma fracionária e justificam essa ocorrência devido ao advento das calculadoras decimais. O uso de frações no nosso dia a dia é percebido na linguagem oral e limita-se a termos como metades, terços e quartos.

Na Matriz de Referência para a Prova Brasil com relação à 4ª série/5º ano, encontramos os números racionais no Tema III – Números e Operações/Álgebra e Funções, nos seguintes descritores:

• D21 - Identificar diferentes representações de um mesmo número racional;
• D22 - Identificar a localização de números racionais representados na forma decimal na reta numérica;
• D23 - Resolver problema utilizando a escrita decimal de cédulas e moedas do sistema monetário brasileiro;
• D24 - Identificar fração como representação que pode estar associada a diferentes significados;
• D25 - Resolver problemas com números racionais expressos na forma decimal envolvendo diferentes significados da adição ou subtração (Brasil, 2011).

Assim como nos PCN, a ênfase da Prova Brasil para a 4ª série/5º ano está na forma decimal do número racional; pouco se refere à forma fracionária (Brasil, 1997).

Diante do exposto percebe-se, com base nas recomendações dos documentos oficiais, que nos anos iniciais do Ensino Fundamental o ensino das frações se resume ao seu conceito, a seus diferentes significados e principalmente à relação parte-todo.

Metodologia

Este trabalho teve inspiração em uma questão levantada nas reuniões semanais realizadas com a equipe do subprojeto do Pibid da Universidade Estadual do Norte do Paraná (UENP) de Matemática do Câmpus de Jacarezinho. Antes de abordá-la, será feita uma descrição da equipe e do cotidiano de funcionamento do subprojeto.

A equipe conta com dois coordenadores, quatro supervisores e 21 bolsistas, divididos em três escolas: uma na cidade de Jacarezinho, uma na cidade de Santo Antônio da Platina e outra em Cambará – todas cidades do Paraná.

Uma estimativa da quantidade de estudantes das escolas públicas atingidos diretamente pelo projeto chega a trezentos alunos do Ensino Fundamental. Os coordenadores são professores e pesquisadores do curso de Licenciatura em Matemática da UENP (Campus de Jacarezinho/PR). Os supervisores são professores do ensino público do Estado do Paraná e lecionam um em Cambará, um em Santo Antônio da Platina e dois em Jacarezinho. Os bolsistas são alunos do curso de Licenciatura em Matemática da UENP e residem nas diversas cidades do entorno da universidade.

A rotina de trabalhos do projeto pode ser descrita assim: os 21 bolsistas são divididos entre os quatro supervisores com base na proximidade do seu local de residência e no número de bolsistas sob a orientação de cada supervisor. O período no qual os bolsistas permanecem na escola participando da aula do supervisor possibilita o contato com a realidade educacional daquela localidade, a observação do comportamento dos alunos e do professor e a realização de intervenções dos bolsistas com o objetivo de aperfeiçoar a aprendizagem de determinado conteúdo pelos alunos e permitir ao bolsista o primeiro contato com a missão de ensinar.

Durante o processo em que o bolsista frequenta a sala de aula são exigidas dele a confecção e a implementação de uma intervenção na sala de aula. O primeiro passo para ocorrerem as intervenções é a separação dos bolsistas assistidos por um supervisor em grupos menores, de dois ou três indivíduos. Esses grupos preparam atividades previamente pensadas e dialogadas com o supervisor e com os coordenadores do subprojeto. O tema e o conteúdo escolhidos são embasados nos PCN para a determinada série. Cada grupo produz o material necessário para que a intervenção ocorra e, em datas estabelecidas, ela acontece.

Nas reuniões quinzenais, os grupos expõem para todos os bolsistas a experiência proporcionada pela intervenção e os resultados obtidos. Uma discussão construtiva se dá e permite que todos os integrantes interajam com os bolsistas responsáveis pela intervenção.

Durante essas discussões, tornou-se recorrente a fala dos bolsistas no que dizia respeito às dificuldades enfrentadas para a realização da intervenção quanto ao comprometimento apresentado pelos alunos e à qualidade da aprendizagem obtida. Em diversas ocasiões relatou-se que, para uma melhor fluidez nas intervenções, era instituído um sistema simples de recompensa. Segundo os bolsistas, essa ferramenta melhorava muito o comprometimento com a atividade realizada e, consequentemente, melhorava a aprendizagem do conteúdo apresentado.

Essa recompensa consistia em promover uma forma de competição entre os estudantes. Ao fim da atividade, os alunos que se saíssem melhor nos trabalhos realizados recebiam um prêmio simbólico. Foi com base nessa questão que surgiu a ideia de verificar se a introdução de alguma forma de competição nas aulas é positiva para a aprendizagem do conteúdo trabalhado.
Com base nessa descrição, procurou-se responder à questão de pesquisa: se a promoção de competição entre os alunos em sala de aula influencia (positiva ou negativamente) o seu respectivo desempenho em determinado conteúdo trabalhado de Matemática.

A investigação do problema teve início com uma reunião com um dos supervisores e os bolsistas que o acompanham em sala de aula. Nessa reunião foi exposta ao supervisor a situação; discutiu-se a forma e o conteúdo que poderiam ser usados para a investigação.

Ficou decidido que a investigação, num primeiro momento, seria realizada em duas turmas de sexto ano, contemplando o reconhecimento da fração como parte de um todo e a significação de numerador e denominador. Esse conteúdo foi escolhido porque teria que ser obrigatoriamente trabalhado durante o ano letivo em que a investigação ocorreu e por não requerer pré-requisito. A necessidade de pré-requisito poderia influenciar no resultado da pesquisa, visto que o domínio ou a falta de domínio do pré-requisito pelo discente é fator determinante na aprendizagem de um novo conteúdo.

O primeiro passo consistiu em um sorteio para decidir em qual turma aconteceria a competição.

O segundo passo foi a aplicação de uma avaliação sobre esse conteúdo nas duas turmas antes mesmo de o conteúdo ser trabalhado em sala de aula. Essa avaliação consistiu em dez questões condizentes com os descritores da Prova Brasil. Cinco questões eram de múltipla escolha e cinco, discursivas. O objetivo da avaliação foi verificar o grau de conhecimento apresentado pelos alunos sobre o conteúdo a ser trabalhado.

O terceiro passo foi expor à turma sorteada que a abordagem a ser utilizada nas próximas aulas seria diferente e que ao fim do período necessário para trabalhar o conteúdo escolhido seria realizada uma nova avaliação e que os seis alunos mais bem classificados no processo avaliativo receberiam uma premiação, sendo três meninas e três meninos. Salientou-se que todos teriam chances iguais de aprendizagem e que, como seria a primeira vez que os alunos entrariam em contato com o conteúdo, ninguém teria a vantagem de já o ter estudado.

Na turma que não foi sorteada, o mesmo conteúdo, com o mesmo número de aulas, foi trabalhado da maneira tradicional adotada pela professora. Não foi feita nenhuma menção sobre o que estava acontecendo na outra turma, a fim de não gerar alguma forma de expectativa.

Ao fim do período necessário para trabalhar o conteúdo escolhido, foi realizada a avaliação nas duas turmas. Os dados foram tabulados e analisados quanto à hipótese de, ao gerar-se um ambiente competitivo na sala de aula, ocorrer aumento na aprendizagem do conteúdo trabalhado.

Para a análise dos dados, foi utilizado coeficiente de variação (CV), que pode ser interpretado como a variabilidade dos dados em relação à média. Quanto menor o CV, mais homogêneo é o conjunto de dados. Tal parâmetro é adimensional, ou seja, será positivo se a média for positiva ou zero quando não houver variabilidade entre os dados. Um CV é considerado baixo (indicando um conjunto de dados razoavelmente homogêneos) quando for menor ou igual a 0,25 (25%) (Montgomery; Runger, 2015).

Na avaliação do desempenho de aprendizagem, utilizou-se como instrumento de análise o ganho relativo médio (g), que é obtido pela razão entre o ganho apurado pelo aluno e o máximo ganho possível com base em duas avaliações idênticas na forma de testes de múltipla escolha: uma antes da apresentação do conceito (pré) e outra após (pós), definido por Hake (1998) como:

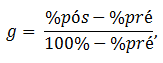
em que %pré corresponde à nota do pré-teste e %pós à nota do pós-teste. O principal mérito de sua utilização é sua invariância para diferentes resultados de pré-teste, dependendo somente do método de instrução utilizado. Para ter-se uma referência, é importante observar os valores típicos de g apresentados na literatura internacional. Para aulas tradicionais (aulas puramente expositivas), os valores de g variam entre 0,1 e 0,2 (Hake, 1998); pesquisas mostram valores de 0,2 e 0,4 para cursos que usaram métodos tradicionais e de engajamento interativo, respectivamente (Barros et al., 2004). Segundo Hestenes, Wells e Swackhamer (1992), porém, em condições usuais de aplicação – como no Ensino de Física na graduação – consideram-se aproveitamentos bons valores de ganhos superiores a 0,6.

Análise e discussão

A análise das informações obtidas com o desenvolvimento do trabalho consistiu em verificar a evolução obtida pelo conjunto de alunos pertencentes às séries 6B (sem competição) e 6D (com competição), com base nos acertos obtidos na avaliação inicial e na final para o conteúdo de frações.

Percebe-se, pela análise da Tabela 1, para a 1ª avaliação, que a média das notas dos alunos pertencentes à turma 6D foi 22,67% maior que a média das notas dos alunos pertencentes à turma 6B. Entretanto, os dados da nota média na 2ª avaliação indicam uma inversão no desempenho obtido pelos alunos. Os discentes pertencentes à turma 6B obtiveram em média nota 11,28% maior que os pertencentes à turma 6D.

Tabela 1: Dados sobre a quantidade de discentes participantes em cada turma, nota média e coeficiente de variação.

*CV = Coeficiente de Variação.

Como observado na Tabela 1, o alto valor do CV obtido para o 6D na primeira avaliação é um indicativo da pouca homogeneidade apresentada pelos discentes dessa turma. Na segunda avaliação, o valor obtido para o CV foi menor, mas não atingiu o valor considerado ideal (menor ou igual a 0,25). A turma 6B apresentou valor inferior para o CV; isso permite verificar que a homogeneidade melhorou em ambas as turmas, porém naquela em que não houve competição foi maior.

Tabela 2: Relação entre as notas obtidas na primeira e na segunda avaliação

Outra análise feita foi sobre o percentual de discentes que obtiveram na segunda avaliação nota superior à primeira avaliação (primeira coluna da Tabela 2). Na turma em que houve competição (6D), 88% dos discentes conseguiram obter a segunda nota maior que a primeira, enquanto na turma que não realizou a competição (6B) esse percentual alcançou 93%.

Os dados da segunda coluna da Tabela 2 indicam que 29,41% dos discentes da turma 6D (com competição) alcançaram nota igual ou superior a cinco na primeira avaliação, enquanto na 6B (sem competição) esse índice foi zero. Na segunda avaliação, 68,75% dos discentes da turma 6B obtiveram nota igual ou superior a 5 e na 6D esse percentual ficou em 58,82%. Verifica-se que na turma em que não houve competição o percentual desses discentes é superior.

A Tabela 3 mostra os resultados para o ganho relativo médio g apresentado no presente estudo. Nela verifica-se que a turma 6B, em que não ocorreu competição, apresentou g de 0,43; esse resultado é maior do que o exibido pela 6D, turma em que a competição ocorreu.

Tabela 3: Resultado médio do ganho relativo médio

Considerações finais

Dentre as inúmeras dificuldades encontradas pelo professor em sala de aula, este trabalho procurou analisar questões relacionadas ao comprometimento apresentado pelos alunos e a qualidade da aprendizagem obtida. Nessa óptica, objetivou-se estudar e analisar a influência do ambiente competitivo na construção do conhecimento de um grupo de discentes do sexto ano do Ensino Fundamental para o conteúdo de frações. Procurou-se responder se a promoção de competição entre os alunos em sala de aula pode influenciar, positiva ou negativamente, o seu desempenho em determinado conteúdo trabalhado de Matemática.

Para tanto, a metodologia foi aplicada em duas turmas de sexto ano de uma escola atendidas pelo mesmo professor. Numa, o conteúdo foi apresentado aos alunos da forma tradicional utilizada pela docente. Noutra, criou-se um ambiente competitivo.

Com respeito aos valores de CV, para a primeira avaliação ficou evidenciada uma não homogeneidade entre os discentes nas duas turmas. Para a segunda avaliação, percebe-se melhora em ambas as turmas, porém a classe em que não houve competição apresentou CV ainda maior. No tocante às notas apresentadas, percebe-se que a turma em que não houve competição apresentou melhores resultados que a outra.

Quanto aos valores do ganho normalizado apresentados pelas classes, pode ser verificado que a turma em que não houve a competição apresentou valor 43,3% maior que o apresentado pela turma em que houve competição, atingindo valor 28,3% abaixo de um valor considerado bom na literatura para tópicos de ensino de Física na graduação.

Após a análise dos resultados obtidos, foi efetuada uma averiguação com os participantes da pesquisa para procurar entender os motivos que levaram os discentes sem competição a obter melhores resultados do que os colegas com competição. Essa verificação apontou como principal fator o fato de os aprendizes se conhecerem e saberem de antemão quais eram os alunos mais capazes e que provavelmente ganhariam a competição. Isso influenciou como fonte de desestímulo aos discentes que se consideravam menos capazes. Corroborava esse fator a fala recorrente de que não adiantaria se esforçar muito para aprender o conteúdo e ganhar a competição, “pois o Fulano e Beltrano são os melhores da sala”, desestimulando seus colegas.

Sugere-se, como estudo subsequente, a verificação da aprendizagem promovendo a competição em equipes, verificando sua efetiva influência na aprendizagem dos estudantes.

Referências

BARROS, J. A.; SILVA, G. S. F.; TAGLIATI, J. R.; REMOLD, J. Engajamento Interativo no curso de Física da UFJF. Revista Brasileira de Ensino de Física, v. 26, nº 1, p. 63-69, 2004.

BERTONI, N. E. Pedagogia: Educação e Linguagem Matemática VI – frações e números fracionários. Brasília: Ed. UnB, 2009.

BRASIL. Plano de Desenvolvimento da Educação: Prova Brasil, Ensino Fundamental, matrizes de referência, tópicos e descritores. Brasília: MEC/SEB/INEP, 2011.

BRASIL. Parâmetros Curriculares Nacionais: Introdução. Ensino Fundamental. Brasília: MEC/SEF, 1998.

BRASIL. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1997.

BRASIL. Lei de Diretrizes e Bases da Educação Nacional. Lei nº 9.394/96, de 20 de dezembro de 1996.

CANTADOR, I.; CONDE, J. M. Effects of competition in education: A case study in an e-learning environment. Proceedings of the International Conference E-learning, IADIS, p.11-18, 2010.

CAPES. Portaria Normativa n° 122, de 16 de setembro de 2009. Dispõe sobre o Pibid - Programa Institucional de Bolsa de Iniciação à Docência, no âmbito da Capes. Capes, 2009. Disponível em: http://www.capes.gov.br/images/stories/download/bolsas/PortariaNormativa122_PIBID.pdf. Acesso em: 26 mar. 2019. 

DOURADO, L. F.; OLIVEIRA, J. F.; SANTOS, C. A. A qualidade da educação: conceitos e definições. Textos para Discussão. Brasília: Inep, 2007. Série Documental.

DRISCOLL, M. P. Psychology of learning for instruction. Needham: Allyn and Bacon, 1994.

FASLI, M.; MICHALAKOPOULOS, M. Supporting active learning through game-like exercises. Proceedings of the 5th IEEE International Conference of Advanced Learning Technologies (ICALT 2005), p. 730-734, 2005.

FREIRE, J. B.; SCAGLIA, A. J. Educação como prática corporal. São Paulo: Scipione, 2003.

FULU, I. A. Enhancing learning through competitions. School of InfoComm Technology, Ngee Ann Polytechnic, 2007.

HAKE, R. R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. American Journal of Physics, v. 66, nº 1, p. 64-74, 1998.

HESTENES, D.; WELLS, M.; SWACKHAMER, G. Force concept inventory. The Physics Teacher, v. 30, nº 3, p. 141-158, 1992.

KIEREN, T. On the Mathematical, cognitive and instructional foundations of rational numbers. In: LESH, R. (Ed.). Number and measurement: paper from a Research workshop. Columbus: Eric/Smeac, 1976. p. 101-144.

LAM, S.-F.; YIM, P.-S.; LAW, J.; CHEUNG, R. The effects of classroom competition on achievement motivation. Proceedings of the 109th Annual Conference of American Psychological Association (APA 2001), 2001.

LAWRENCE, R. Teaching data structures using competitive games. IEEE Transactions on Education, v. 47, nº 4, p. 459-466, 2004.

MONTGOMERY, D. C.; RUNGER, G. C. Estatística aplicada e probabilidade para engenheiros. Rio de Janeiro: LTC, 2015.

PIAGET, J. Seis estudos de Piaget. Trad. Maria Alice Magalhães D’Amorim e Paulo Sérgio Lima Silva. 25ª ed. Rio de Janeiro: Forense Universitária, 2011.

______. O nascimento da inteligência da criança. São Paulo: Crítica, 1986.

PERRENOUD, P. Avaliação: da excelência à regulação das aprendizagens – entre duas lógicas. Porto Alegre: Artes Médicas Sul, 1999.

SHINDLER, J. Transformative classroom management. Pearson Allyn & Bacon Press, 2007.

SIDDIQUI, A.; KHAN, M.; AKHTAR, S. Supply chain simulator: a scenario-based educational tool to enhance student learning. Computers & Education, v. 51, nº 1, p. 252-261, 2008.

THOUSAND, J.; VILLA, R. A.; NEVIN, A. I. Creativity and Collaborative Learning. Brookes Press, 1994.

VERHOEFF, T. The role of competitions in education. Proceedings of the Future World Educating for the 21st Century Conference and Exhibition, 1997.

VOCKELL, E. Educational Psychology: A Practical Approach. Purdue University. 2004.

YU, F.; CHANG, L.; LIU, Y.; CHAN, T.W. Learning preferences towards computerised competitive modes. Journal of Computer-Assisted Learning, v. 18, nº 3, p. 341-350, 2002.