Dominando a Matemática através do dominó – sólidos geométricos

No exercício da docência, podemos enfrentar problemas comuns, como mau comportamento, falta de concentração e falta de interesse e, em especial no ensino de Matemática, pode ser um grande desafio para o professor explicar um conteúdo, por conta da falta de domínio de muitos dos alunos em operações básicas.

Devido a esse cenário, aulas comuns apenas no quadro branco acabam sendo desinteressantes, fazendo-se necessária uma abordagem criativa e mais atrativa dos conteúdos, diversificando as aulas e os espaços de ensino-aprendizagem (além da sala de aula comum), assim como as avaliações (além das tradicionais). Abordagens de temas matemáticos por meio de jogos são defendidas por muitos autores, entre eles D’Ambrosio (1996) e Smole, Diniz, Pessoa e Ishihara (2008), pois jogos bem planejados ajudam a desmistificar a Matemática como extremamente difícil e inalcançável.

Pensando nessa demanda, foi elaborado o projeto Dominando a Matemática através do Dominó - Sólidos Geométricos, atendendo a um público do 2º ano do Ensino Médio, conforme o currículo mínimo da Seeduc-RJ (2012).

Objetivos

Trabalhar em equipe e de forma lúdica, utilizando o dominó como estímulo ao compartilhamento do aprendizado. Segundo o currículo mínimo da Seeduc-RJ (2012), o estudante deve reconhecer características, planificações, propriedades, áreas e volumes de sólidos geométricos.

Metodologia

Numa primeira aula expositiva, com o uso de materiais concretos em acrílico e materiais do cotidiano, foram apresentados os principais sólidos geométricos, identificando primeiramente poliedros e corpos redondos e características similares, como ter duas bases congruentes e paralelas (como no cilindro e prismas), ou ter só uma base e ter um vértice que é ligado a essa base (como no cone e nas pirâmides). Depois, nas aulas seguintes, foi detalhado cada um dos sólidos apresentados, discutindo suas propriedades, áreas e volumes.

Figura 1: Sólidos em acrílico e objetos

A ideia do dominó adaptado a sólidos geométricos também surgiu para atender o projeto Matemática 360º, que serviu como um dos instrumentos de avaliação, com base no Cardápio de ações da Seeduc-RJ. O planejamento das peças ficou sob a responsabilidade do professor; os alunos confeccionaram, apresentaram e jogaram com alunos de outras turmas no dia de culminância do projeto.

Planejamento e criação das peças

Nesse dominó, as peças foram pensadas de maneira que a extremidade de uma, referente a um sólido geométrico, pudesse ser ligada/associada a qualquer extremidade de outra peça referente ao mesmo sólido geométrico e que não pudesse ser ligada/associada a uma extremidade de peça de outro sólido geométrico, equivalente ao que ocorre no dominó comum, em que não podemos ligar extremidades de peças com números diferentes.

Foram consideradas informações variadas: além de informações básicas – apenas os nomes e figuras –, foram colocadas características, planificações, propriedades, áreas e volumes de sólidos geométricos. Foram escolhidos sete sólidos, no lugar dos sete números do dominó tradicional (de 0 a 6).

Figura 2: Sólidos usados no dominó

Quantidade de peças

O jogo tem a mesma quantidade de peças de um dominó comum, ou seja, 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 peças.

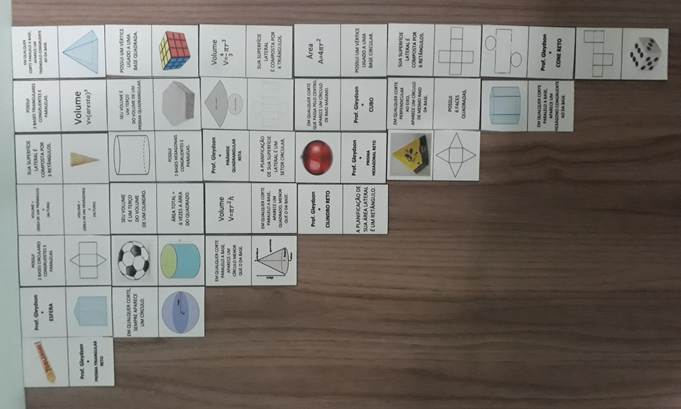
Figura 3: Distribuição triangular das peças do dominó

Confecção das peças

Para visualizar as peças do dominó e para impressão, o interessado deve usar o link arquivo pdf do dominó de sólidos geométricos ou o site do professor Couto (2016) na parte de jogos.

Sugerimos a impressão colorida e em papel de 180 g/m²; não há necessidade de usar papel fotográfico. Após a impressão, na posição de leitura, faça recortes na vertical (entre as peças), depois em cada uma das tiras; faça um recorte no meio e recorte também as bordas, para que as peças fiquem do mesmo tamanho. Para ter maior durabilidade, envolva cada peça com papel adesivo transparente.

Como jogar

As regras são praticamente as mesmas de um dominó comum, mas, para encaixar as peças, as extremidades devem ter informações do mesmo sólido.

Figura 4: Exemplo em que as extremidades não podem se conectar

Figura 5: Exemplo em que as extremidades podem se conectar

O gabão é a peça que tem informações (pode ser nome, figura, planificação, característica etc.) do sólido, tanto na parte de cima quanto na parte de baixo da peça.

Figura 6: Gabões do dominó

Para melhor reconhecimento das peças do dominó, com todas as peças expostas juntas e embaralhadas, deve-se escolher um sólido e separar todas as peças contendo informações desse mesmo sólido; devemos ter sete peças, sendo uma delas o gabão. Depois, pode-se misturar e escolher outro sólido e repetir o processo até fazer com todos os sólidos.

É sugerido que sejam quatro jogadores e que cada jogador fique com sete peças, mas que todas as peças de todos os jogadores fiquem expostas para todos verem e se ajudarem, pois não é exatamente uma competição, mas sim um aprendizado colaborativo. Antes de iniciar o jogo, deve-se solicitar aos jogadores que cada um identifique os gabões que possui (7 gabões no total), depois sortear um sólido para começar pelo seu gabão. Se estiverem disponíveis os sólidos em acrílico ou até mesmo objetos do cotidiano que se assemelham aos sólidos, podem ser expostos para acompanhar o jogo.

Sobre as avaliações propostas

A pontuação total do bimestre é de 10 pontos, distribuídos em pelo menos três instrumentos de avaliação, de acordo com uma portaria da Seeduc-RJ, sendo fixado pela escola um instrumento valendo seis pontos (a tradicional prova individual e sem consulta), ficando os outros quatro pontos livres para que cada professor aplique pelo menos, outros dois instrumentos. Foram utilizados os seguintes instrumentos:

• Jogo de dominó: três pontos. Deve-se confeccionar e testar, depois apresentar e jogar dominó com alunos de outras turmas no dia de culminância do projeto Matemática 360º.
• Avaliação on-line: um ponto, sendo dez questões de múltipla escolha valendo 0,1 cada. Essa avaliação foi feita em formulário Google, com restrição de acesso por login de conta Gmail do aluno, sendo restrito a um envio por aluno, com correção e envio dos resultados apenas após o fim do prazo para todos os alunos. O formulário foi configurado de modo que, em cada acesso, as questões aparecem de forma aleatória, assim como as opções das questões. A avaliação on-line foi disponibilizada pelo site do professor, podendo ser realizada tanto pelo computador quanto no celular.
• Para visualizar e testar um modelo de avaliação on-line que está configurado para correção imediata após o envio e com alguns modelos de questões, é possível acessar o link com um modelo de avaliação on-line sobre sólidos geométricos, adaptado de Couto (2016).
• Simulado: Avaliação em sala, sem pontuação, com resolução de questões com cálculos.

Prova tradicional: seis pontos, em avaliação individual e sem consulta.

Resultados e considerações finais

Verificou-se que essa abordagem, de trabalhar conteúdos matemáticos via dominó é viável e permite um aprendizado de forma lúdica e em equipe. O site do professor Couto (2016) tem disponível para impressão também um dominó com 36 peças, sobre função do 2º grau que foi adaptado e aplicado para alunos de 1º ano do Ensino Médio, de acordo com o currículo mínimo da Seeduc-RJ (2012).

Nesse dominó, apenas alguns poliedros e corpos redondos foram contemplados, mas é possível criar outras versões com 28 peças ou dominós com mais peças, de modo a variar e contemplar uma diversidade maior de sólidos geométricos. Outra possibilidade seria montar um dominó envolvendo apenas poliedros regulares.

Figura 7: Poliedros regulares

Uma observação interessante sobre a quantidade de peças: no dominó com números de 0 a 6, temos sete números, portanto 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 peças; pensando num dominó com números de 0 a 7, temos oito números, portanto 1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 peças. No caso de adaptar o dominó só com poliedros regulares, teremos um dominó equivalente a um dominó com números de 0 a 4, tendo cinco números, portanto 1 + 2 + 3 + 4 + 5 = 15 peças, ou seja, a explicação do número de peças envolve um problema de contagem (combinatória), que também poderia ser abordado empregando o tema progressão aritmética (P. A.), fazendo a soma dos n primeiros termos.

Apesar de serem encontrados alguns dominós prontos e até existir um gerador de dominós no site Só Matemática, nesta proposta apresentou-se uma alternativa mais completa de um dominó de sólidos geométricos, pois, além de nomes e figuras, foram incorporadas informações mais detalhadas, como características e propriedades, que exigem análise mais apurada; nesse tema de Geometria, talvez fosse interessante fazer uma análise segundo a teoria dos Van Hiele, que classifica o pensamento geométrico em diferentes fases, teoria usada em Gonçalves, Ferreira e Ferreira (2017).

O material também foi produzido e disponibilizado para o acervo do Laboratório de Matemática do polo Cederj CGR, servindo também como ideia de material didático para os futuros professores, hoje alunos de licenciatura em Matemática (UFF/Cederj).

Referências

COUTO, Gleydson José Bianquini. Site Professor Gleydson. 2016. Disponível em: http://gleydson-rj.wixsite.com/profgleydsoncouto. Acesso em: 16 jul. 2019.

______. Dominó sobre função do 2º grau. 2018. Disponível em: https://drive.google.com/file/d/1Cbd5eJbtNt3VPuLgMFNbeTSaOjb4c0Z6/view. Acesso em: 16 jul. 2019.

______. Dominando a Matemática com dominó. Revista Appai Educar, nº 117, 2019. Disponível em: https://www.appai.org.br/appai-educacao-revista-appai-educar-edicao-117-dominando-a-matematica-com-domino/. Acesso em: 20 ago. 2019.

______. Avaliação on-line sobre sólidos geométricos. Disponível em: https://drive.google.com/open?id=1hMJDpkH6bt6LxRWIwGwV9aiacdqe1swFeYriqNtnuPI. Acesso em: 16 jul. 2019.

D’AMBROSIO, Ubiratan. Educação Matemática: teoria e prática. Campinas: Papirus, 1996.

GONÇALVES, T. C.; FERREIRA, C. C.; FERREIRA, V. L. D. Geometria Espacial segundo o modelo de Van Hiele: Uma análise do nível de percepção da forma geométrica de alunos que frequentam o terceiro ano do Ensino Médio. 2017. Disponível em: http://www2.bage.ifsul.edu.br/encif2017/index.php/trabalhos/. Acesso em: 16 jul. 2019.

SMOLE, Katia Stocco; DINIZ, Maria I.; PESSOA, Neide; ISHIHARA, Cristiane. Cadernos do Mathema – Ensino Médio – Jogos de Matemática. Porto Alegre: Artmed, 2008.

SÓ MATEMÁTICA. Site. Disponível em: https://www.somatematica.com.br/softOnline/GeradorDominos/gerador.php. Acesso em: 16 jul. 2019.

SEEDUC-RJ. Currículo mínimo de Matemática. 2012. Disponível em: http://www.professores.im-uff.mat.br/hjbortol/disciplinas/2012.2/esp00001/arquivos/seerj.pdf. Acesso em: 16 jul. 2019.

______. Cardápio de ações do projeto Matemática 360º. Disponível em: https://drive.google.com/file/d/1UvVmTQ9LFWVEwI1UlvdNiu3bk6yWLtkm/view. Acesso em: 16 jul. 2019.