Compreendendo a soma de frações com Amoeba, à luz da Teoria dos Registros de Representação Semiótica
Daniela Mendes Vieira da Silva
Doutora em Ensino e História da Matemática e da Física, docente na UCB.
Adriana Luz Fermiano
Licencianda (UCB)
Daniel Alexandre da Rocha
Licenciando (UCB)
Vinicius Maia Ribeiro
Licenciando (UCB)
Marcelo da Silva Godinho
Licenciando (UCB)
Leonardo Pinato
Licenciando (UCB)
Vitor da Silva Ferreira
Licenciando (UCB)
Thiago Aguiar Florencio Lima
Licenciando (UCB)
Júlio César Moreira da Silva
Licenciando (UCB)
Este texto apresenta um material concreto elaborado na disciplina Instrumentação para o Ensino da Matemática I, feito com porções iguais de Amoeba; esse material foi elaborado para auxiliar o processo de ensino-aprendizagem de operações com frações. O uso de flutuadores de piscina recortados não é novo; o que propomos aqui é uma abordagem teoricamente fundamentada para o seu uso no processo de ensino-aprendizagem desse assunto. É sabido que o processo de ensino de operações com frações, em especial da sua soma (e, consequentemente, da subtração, por sua natureza ser compartilhada), tem apresentado dificuldades, o que demanda a elaboração de novas abordagens para a promoção de sua aprendizagem (Pereira; Zuniga, 2015). Os PCN (Brasil, 1998) também destacam a importância do uso de abordagens diversificadas para o ensino de frações.
Para a elaboração do material que aqui propomos, utilizamos a Teoria dos Registros de Representação Semiótica (TRRS), a qual dá suporte a diversos estudos que visam compreender a forma como as pessoas constroem seu conhecimento matemático. Essa teoria tem relação com a representação, o tratamento e a conversão de conceitos matemáticos. Dentro da TRRS, o foco deve estar no aprendiz, o que subordina o objeto a ser ensinado à cognição dele, que se liga às questões de representação. Para Duval (2009), uma das questões centrais relativas ao aprendizado de Matemática é a confusão que normalmente se estabelece acerca de objeto e representação, o que não ocorre, pelo menos em estágios iniciais, em outras ciências. Ele afirma que isso se constitui em um paradoxo cognitivo do pensamento matemático, uma vez que se mostra particularmente difícil não confundir um objeto e sua representação, já que não temos acesso a esse objeto a não ser por meio dela. Dessa forma, tal representação não pode ser literal, visto que um objeto matemático, por mais elementar que seja, ao contrário de objetos concretos, não pode ser acessado a não ser por meio de representações que se façam dele.
Segundo Duval (2009), uma representação tem atreladas a si três atividades cognitivas: primeiramente, constituir um traço ou um ajuntamento de traços perceptíveis que sejam identificáveis como representação de alguma coisa em um sistema determinado; em seguida, transformar as representações apenas pelas regras próprias ao sistema, de modo a obter outras representações que possam constituir uma relação de conhecimento em comparação às representações iniciais; por fim, converter as representações produzidas em um sistema de representações produzidas em um sistema em representações de outro sistema, de tal maneira que estas últimas permitam explicar outras significações relativas ao que é representado (Duval, 2009, p. 37). Portanto, para nos acercarmos de objetos matemáticos devemos forçosamente recorrer a um sistema semiótico. “Para Duval, a noção de registro semiótico de um objeto matemático pode se referir a uma das seguintes modalidades de representação: símbolos, signos, códigos, tabelas, gráficos ou desenhos” (Moutinho; Pais, 2016, p. 3). Para Duval (2009), a apreensão conceitual de um objeto matemático depende da produção e da coordenação de diferentes representações semióticas, uma vez que essa coordenação facilita a diferenciação entre o objeto matemático e sua representação, e a reunião de propriedades do objeto permite um melhor conhecimento acerca dele. À produção de uma representação semiótica, Duval (2009) denomina semiósis e à apreensão conceitual de um objeto através da coordenação de diferentes representações semióticas esse mesmo autor denomina noésis; ou seja, não há noésis sem semiósis.
Na análise do desenvolvimento cognitivo e sua relação com a construção do conhecimento matemático, existem três fenômenos interligados:
- A existência de diversos registros de representação semiótica;
- A diferenciação entre objeto representado e seus registros de representação semiótica;
- A coordenação entre diferentes registros de representação semiótica.
Adiante buscamos aprofundar o entendimento de cada um desses fenômenos. Em relação à existência de diversos registros de representação semiótica, salientamos que um objeto matemático pode ser representado de diferentes maneiras; cada uma dessas formas irá destacar determinado conjunto de suas propriedades. Um exemplo é o número dois: objeto matemático que pode ser representado por um conjunto de dois elementos, pelo símbolo dois, pela palavra dois. A esse respeito, Moutinho e Pais (2016) destacam que: podemos utilizar diferentes formas de representar os objetos matemáticos, mas é importante perceber que determinado tipo de representação de um conhecimento matemático não contém todas as informações desse conhecimento. Um tipo de representação às vezes demonstra uma ideia que outro tipo de representação não é capaz de fazer. Assim, o conhecimento de vários tipos de representação de um mesmo objeto pode ajudar a compreender melhor um conceito matemático (Moutinho; Pais, 2016, p. 3).
Em relação à diferenciação entre objeto representado e seus registros de representação semiótica, reiteramos que nenhuma representação se constitui no objeto matemático em si. Essa confusão é um obstáculo à formação do conceito do objeto.
Existem dois tipos de transformações possíveis para os registros de representação semiótica: o tratamento e a conversão. O tratamento consiste em transformações dentro de um mesmo registro semiótico. Um exemplo é a simplificação da fração 2/4, a partir da qual se obtém o resultado 1/2. Aqui vemos que o sistema semiótico utilizado não se altera, uma vez que toda a transformação acontece dentro da escritura numérica. A conversão que transita entre dois registros, por exemplo: registro de partida = 1/2 e registro de chegada da metade é um tipo de conversão, neste caso, da escritura numérica para a língua natural. Salientamos que “as conversões são as mudanças de registros mais eficazes para a aquisição de um conceito” (Igliori; Maranhão, 2013, p. 60).
Igliori e Maranhão (2013) observam em sua pesquisa que, nos Ensinos Fundamental e Médio, as conversões são menos utilizadas que os tratamentos, e, em caso de utilização de conversões, apenas um sentido é priorizado (por exemplo: lei de formação de uma função/tabela/gráfico, sendo que o sentido inverso gráfico/tabela/função é muito menos utilizado). A dificuldade não é a mesma nos dois sentidos da conversão; tal diferença de dificuldade nos sentidos está associada aos fenômenos de congruência e de não congruência. A congruência acontece quando três critérios entre elementos significantes dos registros de partida e chegada são atendidos simultaneamente; esses critérios estão descritos no Quadro 1.
Tabela 1: Condições necessárias para a existência de congruência na conversão
Critério 1 |
Critério 2 |
Critério 3 |
Possibilidade de uma correspondência “semântica” dos elementos significantes: a cada unidade significante simples de uma das representações pode-se associar uma unidade significante elementar. |
Univocidade semântica terminal: a cada unidade significante elementar no registro da representação de chegada tem um único entendimento possível. |
Organização dos elementos significantes: as organizações respectivas dos elementos significantes de duas representações comparadas conduzem a apreender nelas as unidades em correspondência semântica segundo a mesma ordem de duas representações. |
Fonte: Duval (2009, p.68-69).
Elementos significantes são as menores unidades com significado nas quais podemos decompor um registro. Pode não haver congruência para nenhum desses critérios, para dois ou para somente um. Ou seja, a não congruência entre duas representações admite gradação; isso implica maior ou menor dificuldade na conversão de uma representação, dependendo do grau de não congruência entre a representação de partida e a representação de chegada. No caso de as conversões requeridas não serem congruentes, as dificuldades ou bloqueios dos estudantes com relação à formação do conceito são mais fortes (Duval; 2009; 2013). Ao exemplificar e identificar dificuldades inerentes à coordenação entre registros, evidencia-se que a TRRS de Duval (1999; 2006; 2009; 2013) enfoca as especificidades do sujeito que aprende, e, portanto, “fornece um referencial do funcionamento cognitivo de um aluno diante de uma situação de ensino envolvendo um objeto matemático” (Igliori; Maranhão, 2013, p. 69).
Material proposto
O material proposto é composto uma receita de slime dividida igualmente em cinco partes; essas partes serão os nossos inteiros. Um deles deve ser mantido intacto, o segundo deve ser dividido em dois pedaços (o que resultará em duas frações de 1/2), o terceiro deve ser dividido em três pedaços (o que resultará em três frações de 1/3), o quarto deve ser dividido em quatro pedaços (o que resultará em quatro frações de 1/4) e o quinto deve ser dividido em seis pedaços (o que resultará em seis frações de 1/6).

Figura 1: Divisão do material
Com esse material, o educando fará sempre a alternância entre a representação figural e a escrita numérica do objeto matemático em questão, e isso se dará sempre com congruência máxima, uma vez que as conversões ensejadas pelo material elaborado foram pensadas para sempre atender às suas três condições: a correspondência direta entre os elementos de saída e chegada, o único entendimento do elemento de chegada e a mesma ordem nas operações.
A Figura 1 contempla as três condições, uma vez que ela mostra que, se pegarmos dois pedaços iguais de um flutuador de piscina, recortarmos um em três pedaços iguais e mantivermos o outro deles inteiro, ao convertermos a representação figural para a escrita numérica teremos 1/3 + 1/3 + 1/3 = 1. A representação figural mantém total identidade com a escrita numérica, pois podemos ver claramente que ela reproduz, em números, o que estamos vendo na figura. Os três pedaços representam exatamente 1/3 + 1/3 + 1/3 e que a peça inteira representa exatamente 1, que são as suas traduções em escrita numérica. Ou seja, a figura e a escrita numérica representam a mesma ideia, na mesma ordem, e a escrita numérica tem um único entendimento possível.
Frações como relações parte/todo
Durante grande parte dos anos iniciais, são trabalhados com os alunos os números naturais e suas propriedades. Com isso, é muito natural que, ao se iniciarem os trabalhos com as frações – que pertencem a outro conjunto numérico (o dos números racionais) e que tem propriedades diferentes dos naturais – os estudantes tentem aplicar o que eles já conhecem (os naturais) para encontrar as respostas para o que eles estão conhecendo (os racionais).
Esse tipo de postura se mostra, por exemplo, na resolução da operação 1/2 + 1/2; muitos estudantes somam os numeradores (obtendo 2) e os denominadores (obtendo 4) e chegam ao resultado (incorreto) 2/4. É importante que saibamos que a raiz desse tipo de erro reside no fato de que os alunos estão utilizando propriedades dos naturais para operar com números racionais! Para abordar adequadamente esta problemática, é importante que o professor tenha consciência de que se está operando em um conjunto numérico novo para os alunos e que esse conjunto (racionais) tem as suas especificidades.
Soma ou subtrai o numerador e repete o denominador, por quê?
Antes de partirmos para a operação em si, é primordial que entendamos com o que estamos operando e o que isso significa. As frações são relações parte/todo, nas quais o numerador indica com quantas partes estamos operando e o denominador indica em quantas partes o todo foi dividido.
Denominadores iguais: o caso 1/2 + 1/2
Vamos a um exemplo: retomando a operação 1/2 + 1/2, o que temos? Observando a Figura 2, vemos que temos duas metades sendo somadas, ou seja, o 2 no denominador indica em quantos pedaços as nossas frações estão divididas e o 1 no numerador indica quantos pedaços nós temos para operar. O material concreto que ora propomos ilustra essa situação.

Figura 2: 1/2+1/2
Quando somamos duas metades, nós alcançamos um inteiro, como é possível ver na Figura 3.
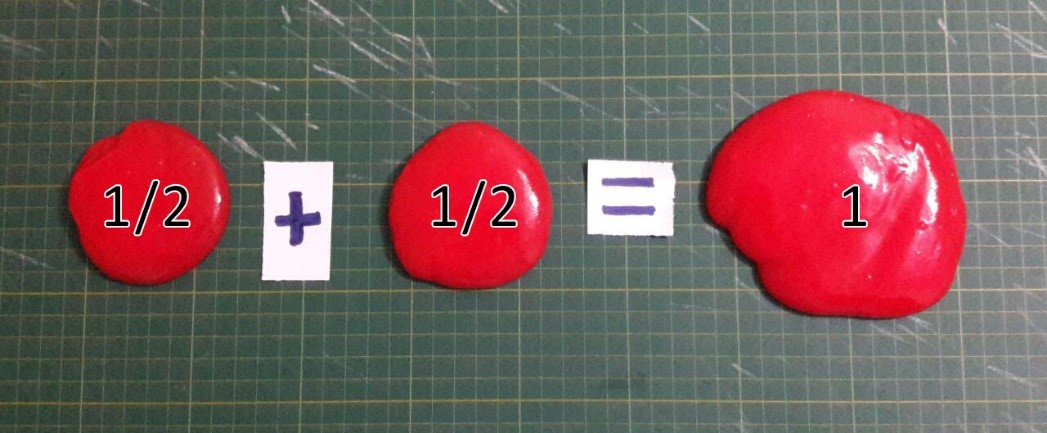
Figura 3: 1/2 + 1/2 = 1
Ora, com o material proposto é mais fácil ver que estamos somando duas metades e que o resultado dessa soma deve ser um inteiro. Aqui as propriedades das frações saltam aos olhos, e é por esse motivo que indicamos o uso desse material para apresentar o novo conjunto numérico das frações, assim como as novas propriedades que serão trabalhadas.
Denominadores diferentes: O caso 1/2 + 1/4
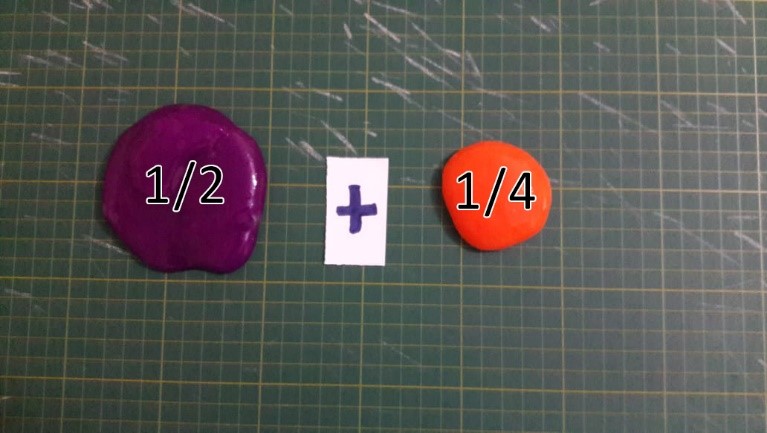
Figura 4: 1/2 + 1/4
Usando o material, podemos visualizar o motivo pelo qual não podemos fazer essa soma diretamente, uma vez que se trata de coisas diferentes a serem somadas. Por esse motivo, teremos que fazer trocas do material que temos em mãos visando ter peças iguais para somente depois operarmos. Para começar, vamos trocar a peça maior, 1/2, por duas peças de 1/4. Veja na Figura 5 que é possível fazer a troca de uma peça de 1/2 por duas peças de 1/4, pois teremos a mesma quantidade de flutuador em ambos os casos.
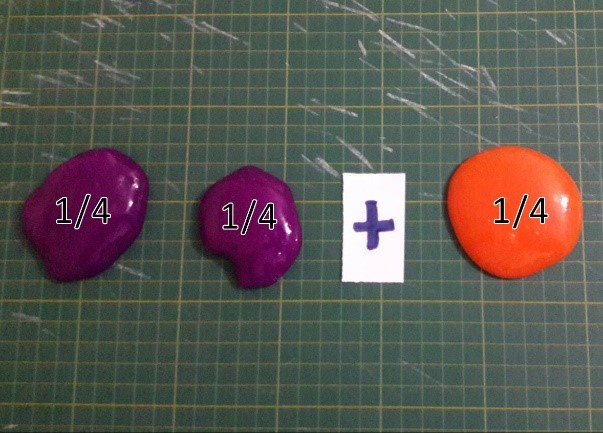
Figura 5: Trocando uma peça de 1/2 por duas peças de 1/4
Com todas as peças de mesmo tamanho em mãos, chegamos à solução 3/4; para isso, basta contar quantas peças de 1/4 temos em mãos.

Figura 6: 1/4 + 2/4 = 3/4
Denominadores não múltiplos: o caso 1/2 + 1/3
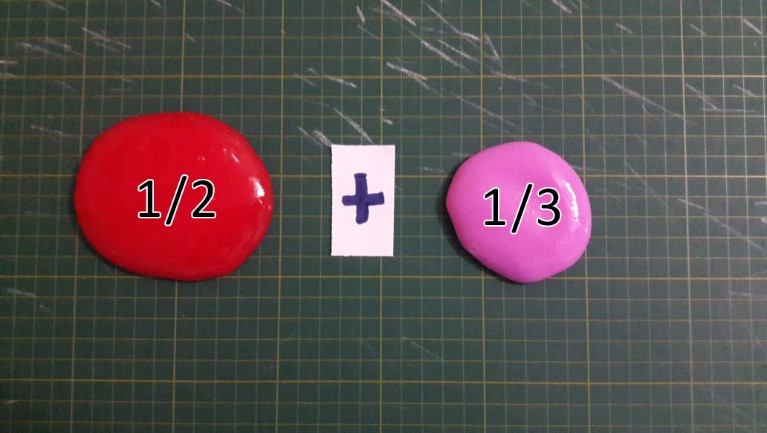
Nessa situação, e já de posse da informação de que, para que possamos operar os flutuadores, eles devem estar cortados na mesma quantidade de pedaços, basta dividir cada flutuador em um múltiplo de ambos os denominadores – por exemplo, 6.

Figura 7: 1/3 = 2/6

Figura 8: 1/2 = 3/6
Com as trocas efetuadas, passamos a ter a seguinte operação: 2/6 + 3/6; e a solução 5/6 surge quando reunimos os pedaços iguais, como pode ser visto na Figura 9.

Figura 9: 2/6 + 3/6 = 5/6
Considerações finais
Entendemos, com base no que mostramos aqui, que o material proposto atende às necessidades que destacamos no presente artigo, assim como traduz os fenômenos de congruência nas conversões entre representações semióticas propostas por Duval (2009) como facilitadores do aprendizado de Matemática. E que esse material pode ser, portanto, um auxiliar no processo de ensino-aprendizagem de soma de frações. Destacamos que todas as outras operações com frações podem ser efetuadas com esse material; apenas não as abordamos porque foge ao escopo do presente trabalho.
Referências
BRASIL. Parâmetros Curriculares Nacionais de Matemática. 1998. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/matematica.pdf. Acesso em: 17 fev. 2019.
D’AMORE, B. Elementos de didática da Matemática. Tradução de Maria Cristina Bonomi Barufi. São Paulo: Livraria da Física, 2007.
DUVAL, R. Registros de Representação Semiótica e funcionamento cognitivo da compreensão em Matemática. In: MACHADO, S. D. A. (Org.). Aprendizagem em Matemática: Registros de Representação Semiótica. Campinas: Papirus, 2013.
_____. Semiósis e pensamento humano – Registros semióticos e aprendizagens intelectuais (fascículo 1). São Paulo: Livraria da Física, 2009.
______. Representation, vision and visualization: cognitive functions in mathematical thinking. Basic issues for learning, 1999.
_____. A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 2006.
IGLIORI, S.B.C.; MARANHÃO, M. C. Registros de Representação e Números Racionais do livro: aprendizagem de Matemática. In: ALCÂNTARA MACHADO, Silvia Dias (Org.). Aprendizagem de Matemática – Registros de Representação Semiótica. Campinas: Papirus, 2013. p. 57-70.
MOUTINHO, I.; PAIS, R. B. Diversificação de recursos para o ensino de números nos primeiros anos escolares. Anais do XII Encontro Nacional de Educação Matemática.
PEREIRA, T. S., ZUNIGA, N. O. C. Uma investigação sobre as dificuldades dos alunos das séries iniciais do ensino médio envolvendo frações. 2015. Disponível em: http://www.ufjf.br/emem/files/2015/10/UMA-INVESTIGA%C3%87%C3%83O-SOBRE-AS-DIFICULDADES-DOS-ALUNOS-DAS-S%C3%89RIES-INICIAIS-DO-ENSINO-M%C3%89DIO-ENVOLVENDO-FRA%C3%87%C3%95ES.pdf. Acesso em: 18 fev. 2019.
Publicado em 28 de abril de 2020
Como citar este artigo (ABNT)
SILVA, Daniela Mendes Vieira da; FERMIANO, Adriana Luz; ROCHA, Daniel Alexandre da; RIBEIRO, Vinicius Maia; GODINHO, Marcelo da Silva; PINATO, Leonardo; FERREIRA, Vitor da Silva; LIMA, Thiago Aguiar Florencio; SILVA, Júlio César Moreira da. Compreendendo a soma de frações com Amoeba, à luz da Teoria dos Registros de Representação Semiótica. Revista Educação Pública, v. 20, nº 15, 28 de abril de 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/15/compreendendo-a-soma-de-fracoes-com-amoeba-a-luz-da-teoria-dos-registros-de-representacao-semiotica-uma-proposta-pedagogica-nascida-das-aulas-de-instrumentacao-para-o-ensino-de-matematica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

