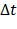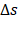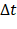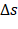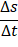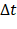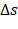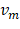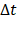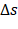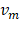Estudo do movimento uniforme subsidiado pela plataforma Desmos: uma proposta pedagógica
Daniela Mendes Vieira da Silva
Aluna de Tecnologias Digitais no Ensino de Matemática e Ciências, doutoranda de Ensino e História da Matemática e da Física (Pemat/UFRJ)
Paula Monteiro
Aluno de Tecnologias Digitais no Ensino de Matemática e Ciências, doutorando de Ensino e História da Matemática e da Física (Pemat/UFRJ)
Vitor Acioly
Aluno de Tecnologias Digitais no Ensino de Matemática e Ciências, doutorando de Ensino e História da Matemática e da Física (Pemat/UFRJ)
A tecnologia impregna de sentidos nosso estar no mundo, e a escola não está apartada dessa impregnação. Nossos alunos são, como nós, habitantes do ciberespaço, cotidianamente influenciando e sendo influenciados por ele. Somos habitantes da sociedade hiperconectada e nela interagimos continuamente pelas telas de nossos dispositivos móveis. Portanto, o aprendizado, na contemporaneidade, passa pelas telas de nossos smartphones (Santaella, 2010).
A aprendizagem via aplicativos de smartphones é conhecida como App Learning. Por meio de aplicativos é possível ter acesso à informação, interagir com pares, construir e compartilhar conhecimentos de forma colaborativa, sem a necessidade de um polo físico. Além disso, o fato de a interação acontecer em um não lugar traz como vantagem inequívoca a derrubada de todas as fronteiras e distâncias físicas, ampliando em escala global o alcance de interação com outros atores nesse processo (Alves; Porto, 2018). Como Santos (2011), entendemos, portanto, que uma rede social unindo a docência à aprendizagem pode ser criada por meio de aplicativos de celular. Subsidiada por eles, a aprendizagem pode acontecer dentro desse contexto internético e hiperconectado no qual os nossos jovens estão inseridos e no qual os seus processos de aprendizagem ocorrem.
As interações entre esses atores ocorrem via interfaces informacionais, que são portas para o ciberespaço e por meio das quais “produzimos e negociamos sentidos, educamos e nos educamos, formamos e nos formamos, pesquisamos e somos pesquisados” (Santos; Weber, 2014, p. 2). Ou seja, é por meio dessas portas conectadas por bits e bytes que adentramos o ciberespaço e podemos ter acesso não só ao outro, mas também a conteúdos diversos que podemos livremente compartilhar, assistir, indicar a audiência através de links etc. E isso acontece o tempo todo, em tempo real ou não, uma vez que até a barreira do tempo é contornada pelas ferramentas assíncronas oferecida por redes sociais, pois as interações vivenciadas ali ficam armazenadas para acesso.
As ferramentas do App Learning, aliadas à nova configuração dos seres-humanos-com-internet destacados por Borba e Souto (2016), facilitam o engajamento dos atores envolvidos em atividades propostas interfaceadas por aplicativos. Devemos também destacar que, se por um lado temos engajamento e ferramentas diversas a nosso favor, por outro lado temos a velocidade na qual essas interações acontecem. Tudo, nesse universo, tende a ser mais rápido e mais fluido, o que pode levar a discussões ricas em subsídios, porém sem aprofundamento.
Nossa opção por elaborar atividades subsidiadas por um aplicativo de celular decorre dessa inserção do estudante do século XXI nessa realidade hiperconectada, na qual os smartphones podem ser entendidos como extensão de seus corpos e a internet pode ser vista como uma extensão de suas memórias, podendo ser entendidos, portanto, como órteses, no sentido de que ampliam a capacidade humana (Esquincalha, 2019).
Dentro desse contexto, entendemos ser importante elaborar um conjunto de atividades que utilizassem um aplicativo de celular para discutir uma temática comum aos autores do presente artigo – duas professoras de Matemática e um professor de Física. Escolhemos o Movimento Uniforme, pois essa é uma temática que pudemos integrar facilmente tanto à disciplina de Física como à disciplina de Matemática e que normalmente é abordada de forma separada nas escolas. Em um contexto escolar, o Movimento Uniforme é estudado na Física, e a função afim é estudada na Matemática de forma completamente separada, como se eles nada tivessem em comum.
Diante do exposto, como objetivo geral buscamos compor um conjunto de atividades subsidiadas pelo software Desmos para o estudo integrado, entre as disciplinas de Matemática e Física, do Movimento Uniforme e da velocidade instantânea. Desmos é um software/aplicativo de Matemática dinâmico que oferece um ambiente virtual para aprendizagem e ensino da Matemática.
Como objetivos específicos, tencionamos elaborar duas atividades subsidiadas pelo software visando facilitar o entendimento:
- da representação do movimento por meio de sua função posição (Atividade 1);
- da caracterização do movimento uniforme (Atividade 2); da representação do movimento uniforme por meio de sua função posição (Atividade 2); da classificação dos movimentos em movimentos uniformes e movimentos variados (Atividade 2).
Este trabalho é estruturado com esta introdução, em seguida há uma justificativa na qual será explicada a escolha do aplicativo Desmos e suas vantagens, seguida por um item denominado proposta pedagógica, no qual apresentamos as duas atividades, ilustrando-as com imagens do software Desmos, e concluindo com as considerações finais e bibliografia.
Justificativa da escolha do Desmos
Um dos segmentos que mais consome conteúdos da internet são estudantes, professores e profissionais interessados em ferramentas práticas e que tenham relação de produtividade. A escolha do Desmos vem no sentido de permitir a estudantes ou professores usar seu próprio smartphone de uma maneira mais significativa do que uma simples calculadora científica, além de ser um app gratuito, o que facilita para tornar acessível a todos.
O Desmos é uma calculadora gráfica que pode ser adquirida de forma gratuita e utilizada em diversos aparatos tecnológicos, como um computador em um browser (navegador) ou realizando download em iOS ou Android. A melhor característica do Desmos são suas funcionalidades, pois não há diferença entre elas no uso em uma página de internet em um computador ou em um celular, além de conceder acesso offline.
O objetivo deste aplicativo, além de uma representação gráfica, é motivar os estudantes a escreverem qualquer expressão matemática, mesmo que tenha relação com outras disciplinas como a física. É fazer com que eles percebam que inserindo um número ilimitado de expressões matemáticas, instantaneamente os resultados serão representados graficamente, podendo variar suas cores, das diferentes características e nos desenhos mais complexos.
Ao terminarem uma atividade, os estudantes podem imprimir os resultados, além de poderem compartilhar em redes sociais como Facebook, Twitter e Google. No site oficial do Desmos, são disponibilizados diversos vídeos e textos que explicam com detalhes como montar gráficos, adicionar tabelas e como relacionar com alguns conceitos matemáticos.
Proposta pedagógica
Propomos que as atividades aqui apresentadas sejam aplicadas a alunos a partir do primeiro ano do ensino médio, uma vez que tais atividades exigem o domínio nos conceitos básicos relativos às funções.
Entendemos que estas atividades podem contribuir para o aprendizado dos conceitos matemáticos e físicos relacionados ao Movimento Uniforme porque a plataforma Desmos possibilita uma abordagem dinâmica das atividades apresentadas para o estudo dos conceitos em questão.
Atividade 1
A Atividade 1 foi inspirada em Ramalho Jr., Ferraro e Soares (2015, p. 43) e aborda a função posição do movimento uniforme no Desmos. Apresentamos no Quadro 1 a definição de espaço.
Quadro 1: Definição de espaço

Fonte: Ramalho Jr., Ferraro; Soares (2015, p. 43)
A primeira atividade tem como objetivo levar o aluno a compreender a representação do movimento por meio de sua função posição, função que relaciona o espaço s com os correspondentes instantes t do objeto e é representada genericamente por s=f(t). O espaço inicial (s0) é o espaço do móvel no instante t = 0. A Atividade 1 foi dividida em três tarefas, a Tarefa 1 apresenta um movimento progressivo, a Tarefa 2 apresenta um movimento retrógrado e a Tarefa 3 apresenta um movimento inicialmente retrógrado e, depois, progressivo.
Para começar, propomos, como Tarefa 1, que seja indicado ao estudante o preenchimento no Desmos (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem) da Tabela 1 que relaciona o tempo ao espaço e na qual valores aleatórios devem ser inseridos para o tempo (variável livre) e, a partir dessa inserção, o espaço deve ser calculado (variável dependente).
Tabela 1: Relacionando tempo x espaço 1
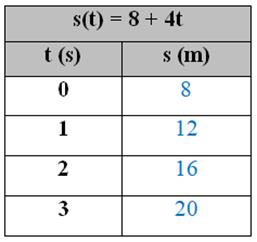
Podemos observar os desdobramentos da tabela preenchida no Desmos (Figura 1). Inicialmente, o estudante deve inserir a função que determina o movimento da partícula (s(t) = 8 + 4t), na sequência ele deve preencher a tabela, a qual utiliza essa função, para determinar os pares ordenados de variáveis livres e dependentes associados. Esses pares ordenados serão plotados na interface gráfica do Desmos.
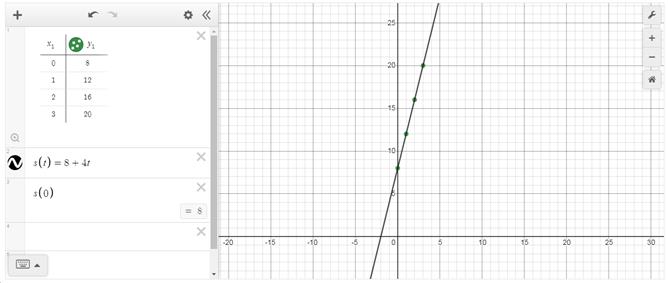
Figura 1: Atividade 1, Tarefa 1 no Desmos
Após a manipulação da função, propomos ao aluno, para finalizar a tarefa, a elaboração de um pequeno relato baseado nas observações do aluno quanto a esta manipulação no Desmos. Esperamos, com esta atividade e relato, que o estudante perceba que o espaço percorrido pelo móvel aumenta em intervalos regulares no decorrer do tempo. Em Física, quando os espaços do móvel crescem no decorrer do tempo, o movimento é denominado progressivo.
Como Tarefa 2 da primeira atividade, mantemos a estrutura da tarefa anterior, modificando a função proposta. Para começar esta etapa, propomos que seja indicada ao estudante o preenchimento (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem) da Tabela 2 que relaciona o tempo ao espaço e na qual valores aleatórios devem ser inseridos para o tempo (variável livre) e, a partir dessa inserção, o espaço deve ser calculado (variável dependente).
Tabela 2: Relacionando tempo e espaço 2
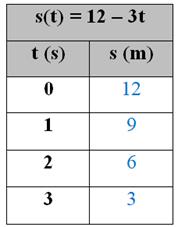
Podemos observar os desdobramentos da tabela preenchida no Desmos (Figura 2). Inicialmente, o estudante deve inserir a função que determina o movimento da partícula (s(t) = 12 - 3t), na sequência ele deve preencher a tabela, a qual utiliza esta função, para determinar os pares ordenados de variáveis livres e dependentes associados. Esses pares ordenados serão plotados na interface gráfica do Desmos.
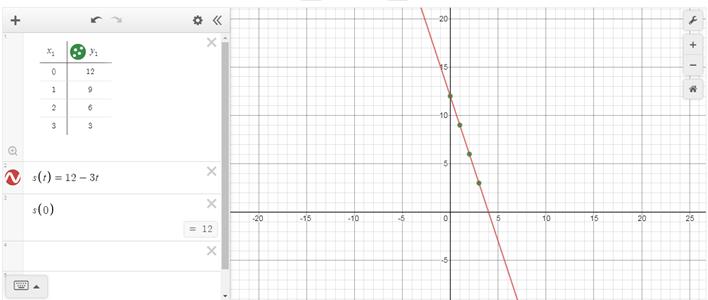
Figura 2: Atividade 1, Tarefa 2 no Desmos
Após a manipulação da função, propomos, para finalizar a tarefa, a elaboração de um pequeno relato baseado nas observações do aluno quanto a esta manipulação no Desmos. Esperamos com esta atividade e relato que o estudante perceba que o espaço percorrido pelo móvel decresce em intervalos regulares no decorrer do tempo. Em Física, quando os espaços do móvel decrescem no decorrer do tempo, o movimento é denominado retrógrado.
Propomos, como Tarefa 3, que seja indicado ao estudante o preenchimento (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem) da Tabela 3, que relaciona o tempo ao espaço e na qual valores aleatórios devem ser inseridos para o tempo (variável livre) e, a partir dessa inserção, o espaço deve ser calculado (variável dependente).
Tabela 3: Relacionando tempo e espaço 3
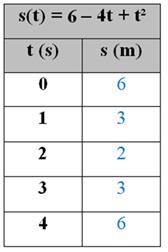
Após o preenchimento da tabela supracitada, podemos observar os desdobramentos da tabela preenchida no Desmos (Figura 3). Inicialmente, o estudante deve inserir a função que determina o movimento da partícula (s(t) = 6-4t+t²), na sequência ele deve preencher a tabela, a qual utiliza esta função, para determinar os pares ordenados de variáveis livres e dependentes associados. Esses pares ordenados serão plotados na interface gráfica do Desmos.
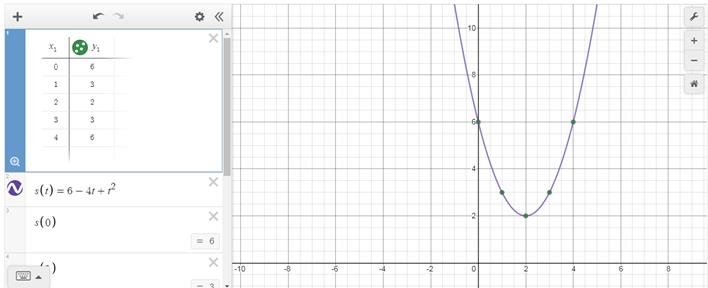
Figura 3: Atividade 1, Tarefa 3, no Desmos
Após a manipulação da função, propomos, para finalizar a tarefa, a elaboração de um pequeno relato baseado nas observações do aluno quanto a esta manipulação nos Desmos. Esperamos com esta atividade e relato que o estudante perceba que o espaço percorrido pelo móvel inicialmente decresce em intervalos não regulares no decorrer do tempo e após certo ponto cresce nas mesmas condições. Neste caso, para a Física, o movimento desse móvel foi inicialmente retrógrado e, depois, progressivo.
Atividade 2
A Atividade 2 aborda a velocidade escalar (média ou instantânea). Para iniciar essa atividade, é apresentada ao aluno a definição de variação de espaço de um ponto material em determinado intervalo de tempo (quadro 2).
Quadro 2: Definição de velocidade média

Fonte: Ramalho Jr., Ferraro; Soares (2015).
Propomos, como Tarefa 1 da segunda atividade, que seja indicado ao estudante o preenchimento da Tabela 4 no Desmos calculando a variação do espaço a partir dos dados coletados na Tabela 1 que relaciona o intervalo de tempo com a variação do espaço do ponto material.
Tabela 4: Variação do espaço
Instante inicial |
Instante final |
|
|
t = 0 |
t = 1 |
1 |
4 |
t = 1 |
t = 2 |
1 |
4 |
t = 2 |
t = 3 |
1 |
4 |
Após o preenchimento da tabela, propomos a elaboração de um pequeno relato baseado nas observações do aluno. Esperamos com esta atividade e relato que o estudante perceba que o espaço percorrido pelo móvel é regular e igual a 4 metros a cada segundo. Em Física, um movimento é uniforme quando o móvel percorre distâncias iguais em intervalos de tempos iguais. Em Matemática, a regularidade destes remete à função afim.
Dando continuidade à tarefa, sugerimos que os estudantes calculem 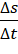 no Desmos para cada intervalo de tempo
no Desmos para cada intervalo de tempo  citado abaixo e preencham a Tabela 5 (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem).
citado abaixo e preencham a Tabela 5 (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem).
Tabela 5: Velocidade Média
Instante inicial |
Instante final |
|
|
|
t = 0 |
t = 2 |
2 |
8 |
8 / 2 = 4 |
t = 0 |
t = 3 |
3 |
12 |
12 / 3 = 4 |
t = 1 |
t = 3 |
2 |
8 |
8 / 2 = 4 |
Após este preenchimento sugerimos que o aluno relate o observado, na tabela que preencheu no item anterior, sobre o quociente 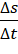 para cada intervalo de tempo citado. Esperamos que o estudante perceba que não importa o quanto
para cada intervalo de tempo citado. Esperamos que o estudante perceba que não importa o quanto  e
e 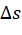 variem, o quociente será sempre 4. Em Física, a velocidade escalar média
variem, o quociente será sempre 4. Em Física, a velocidade escalar média  no intervalo de tempo
no intervalo de tempo  é expressa pela relação (Quadro 3).
é expressa pela relação (Quadro 3).
Quadro 3: Cálculo da Velocidade Média
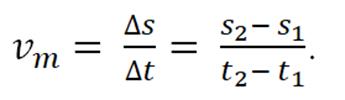
Após esta constatação propomos que o estudante analise, no Desmos, à luz do conceito de função afim, a função posição s(t) = 8 + 4t, a posição no instante t = 0 e a velocidade média escalar (o quociente 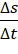 ) e que relate suas observações. Esperamos que ao final de seu relato, ele seja capaz de identificar que na função do 1° grau s(t), o termo independente é 8 = t0 e o coeficiente linear é 4 = vm. Atenção! Em Física, a função posição no movimento uniforme,
) e que relate suas observações. Esperamos que ao final de seu relato, ele seja capaz de identificar que na função do 1° grau s(t), o termo independente é 8 = t0 e o coeficiente linear é 4 = vm. Atenção! Em Física, a função posição no movimento uniforme, 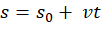 , é uma função do 1° grau em t, onde s0 é o espaço do móvel no instante t = 0 e v é a velocidade escalar média.
, é uma função do 1° grau em t, onde s0 é o espaço do móvel no instante t = 0 e v é a velocidade escalar média.
Como segunda tarefa da segunda atividade, propomos que seja indicado ao estudante o preenchimento, no Desmos, da Tabela 6 (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem) calculando velocidade média escalar a partir dos dados coletados na Tabela 2 que relaciona o intervalo de tempo com a variação do espaço do ponto material.
Tabela 6: Velocidade Média 2
Instante inicial |
Instante final |
|
|
|
t = 0 |
t = 3 |
3 |
- 9 |
- 9 / 3 = - 3 |
t = 1 |
t = 3 |
2 |
- 6 |
- 6 / 2 = - 3 |
t = 2 |
t = 3 |
1 |
- 3 |
- 3 / 1 = - 3 |
Após este preenchimento sugerimos que o aluno relate o observado, na tabela que preencheu no item anterior, sobre o quociente 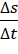 para cada intervalo de tempo citado. Esperamos, ao final do relato, que o estudante perceba que a Velocidade Média encontrada é negativa e igual a – 3, não importando o quanto
para cada intervalo de tempo citado. Esperamos, ao final do relato, que o estudante perceba que a Velocidade Média encontrada é negativa e igual a – 3, não importando o quanto  e
e 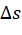 variem.
variem.
Em Física, quando o movimento é retrógrado, isto é, o móvel se desloca contra a orientação positiva da trajetória, a velocidade escalar do móvel é negativa. Já no movimento progressivo, o móvel se desloca a favor da orientação positiva da trajetória, a velocidade escalar do móvel é positiva. Assim, temos que a função posição no movimento uniforme, 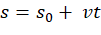 , terá v>0 quando o movimento é progressivo e v<0 quando o movimento é retrógrado.
, terá v>0 quando o movimento é progressivo e v<0 quando o movimento é retrógrado.
Como Tarefa 3 da segunda atividade, propomos que seja indicado ao estudante o preenchimento da Tabela 7 (em preto o que foi recebido pelos estudantes, em azul o que esperamos que eles completem) calculando velocidade escalar média 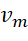 para cada intervalo de tempo
para cada intervalo de tempo  citado abaixo e que relate suas observações.
citado abaixo e que relate suas observações.
Tabela 7: Velocidade média 3
Instante inicial |
Instante final |
|
|
|
t = 0 |
t = 1 |
1 |
- 3 |
- 3 |
t = 1 |
t = 2 |
1 |
- 1 |
- 1 |
t = 2 |
t = 3 |
1 |
+ 1 |
+ 1 |
t = 3 |
t = 4 |
1 |
+ 3 |
+ 3 |
t = 3 |
t = 3 |
3 |
- 3 |
- 1 |
t = 0 |
t = 4 |
4 |
0 |
0 |
Esperamos, ao final do relato, que o estudante perceba que a Velocidade Média não foi constante. Em Física, a velocidade escalar instantânea v pode ser entendida como uma velocidade escalar média, 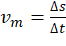 , para um intervalo de tempo
, para um intervalo de tempo  extremamente pequeno.
extremamente pequeno.
Se a velocidade escalar é mesma em todos os instantes, ela coincide com a velocidade escalar média, qualquer que seja o intervalo de tempo considerado (Quadro 4).
Quadro 4: Velocidades escalar média e instantânea
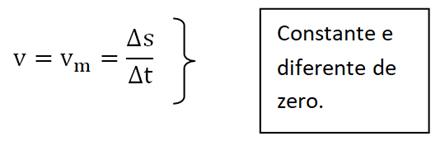
Assim, é definido que movimentos que possuem velocidade escalar instantânea constante e não nula são chamados de movimentos uniformes. Já os movimentos cuja velocidade escalar varia com o tempo são chamados de movimentos variados.
Considerações finais
O presente artigo apresentou uma proposta de atividade que relaciona conteúdos das disciplinas física e matemática, através da análise da usabilidade de um aplicativo gratuito. Entendendo a necessidade de melhorias nas metodologias de ensino, em conjunto com facilidade do uso de celulares, é apresentado uma opção que pode facilitar o entendimento das disciplinas matemática e física através de um aplicativo educacional.
Contudo, vale ressaltar que alguns pontos e novas abordagens podem ser revistos em trabalhos futuros, bem como a realização de novas atividades. Conforme apresentado anteriormente, os conceitos escolhidos precisam ser trabalhados em conjunto, e dependem de professores de disciplinas diferentes, e para o aproveitamento de maneira mais eficaz o uso da plataforma escolhida deve ser atribuído dentro do contexto escolar.
A proposta de atividade sugere que os conteúdos devem possuir uma afinidade, como a proposta nesse artigo: Movimento Uniforme e Função do primeiro grau, onde os conceitos básicos se relacionam.
É interessante mencionar o uso da plataforma Desmos, como um aplicativo gratuito e de fácil acesso e boa interface, pois amplia as possibilidades no uso nos mais divergentes públicos de ensino médio, além de possuir tutoriais gratuitos para professores.
Referências
ALVES, A. L.; PORTO, C. M.; OLIVEIRA, K. E. J. Educação online mediada pelo WhatsApp: mapeando rastros e controvérsias de alunos à luz da teoria ator-rede. Rev. Diálogo Educ., Curitiba, v. 18, n. 56, p. 164-185, jan./mar. 2018.
BORBA, M. C.; SOUTO, D. L. P. Seres humanos-com-internet ou internet-com-seres humanos: uma troca de papéis? Relime, v. 19(2), 2016.
ESQUINCALHA, Agnaldo. Notas de aula da disciplina Tecnologias do Programa de Pós Graduação em Ensino de Matemática da UFRJ. 2019.
RAMALHO Jr., F.; FERRARO, N. G.; SOARES, P. A. de T. Os fundamentos da física. 11ª ed. São Paulo: Moderna, 2015.
SANTAELLA, L. A aprendizagem ubíqua substitui a educação formal? Revista de Computação e Tecnologia da PUC-SP, São Paulo, v. 2, nº 1, p. 17-22, out. 2010. http://dx.doi.org/10.20952/revtee.v0i0.3446.
SANTOS, Rosemary. A tessitura do conhecimento via mídias digitais e redes sociais: itinerâncias de uma pesquisa-formação multirreferencial. 2011. 232 f. Dissertação (Mestrado em Educação) – Faculdade de Educação, Universidade do Estado do Rio de Janeiro, Rio de Janeiro, 2011.
SANTOS, E. WEBER, A. Diários on line, cibercultura e pesquisa-formação multirreferencial. 2014. Disponível em: < http://www.uece.br/endipe2014/ebooks/livro1/205-%20DI%C3%81RIOS%20ONLINE,%20CIBERCULTURA%20E%20PESQUISA-FORMA%C3%87%C3%83O%20MULTIRREFERENCIAL.pdf>. Acesso em: set. 2018.
STEWART, J. Cálculo. Vol. I. 6ª ed. São Paulo: Cengage Learning, 2011.
UNIVERSIDADE DE BRASÍLIA. DEPARTAMENTO DE MATEMÁTICA. Cálculo 1 - Velocidade instantânea. s/d. Disponível em: http://mat.unb.br/calculo1m/Textos/Modulo1/Semana1/velocidade-instantanea.pdf. Acesso: 11 maio 2019.
Versão Desmos na internet: https://teacher.desmos.com/
Este artigo foi elaborado na disciplina Tecnologias Digitais no Ensino de Matemática e Ciências, ministrada pelo prof. dr. Agnaldo Esquincalha, no doutorado em Ensino e História da Matemática e da Física (Pemat/UFRJ).
Publicado em 26 de maio de 2020
Como citar este artigo (ABNT)
SILVA, Daniela Mendes Vieira da; MONTEIRO, Paula; ACIOLY, Vitor. Estudo do movimento uniforme subsidiado pela plataforma Desmos: uma proposta pedagógica. Revista Educação Pública, v. 20, nº 19, 26 de maio de 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/19/estudo-do-movimento-uniforme-subsidiado-pela-plataforma-desmos-uma-proposta-pedagogica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.