A percepção dos alunos de Ensino Médio de uma escola pública sobre o ensino de Matemática
Adriana Oliveira Bernardes
Professora de Física da rede pública estadual do Rio de Janeiro (Seeduc/RJ), doutoranda em Ensino e História da Matemática e da Física (Pemat/UFRJ)
Adriana de Souza Lima
Professora de Matemática das redes públicas estadual e municipal do Rio de Janeiro (Seeduc/RJ/SME/RJ), doutoranda em Ensino e História da Matemática e da Física (Pemat/UFRJ)
Victor Giraldo
Doutor, professor do Programa de Ensino e História da Matemática e da Física (UFRJ)
Inicialmente criado para ser um instrumento de avaliação da qualidade do Ensino Médio no país, o Exame Nacional do Ensino Médio (Enem) tornou-se, desde 2009, o principal critério de seleção de estudantes que pretendem ingressar em boa parte das instituições brasileiras de Ensino Superior. Ao finalizarem a Educação Básica obrigatória, dos 4 aos 17 anos, os estudantes que prestam o Enem são avaliados em quatro áreas do conhecimento: 1) Ciências Humanas e suas tecnologias; 2) Ciências da Natureza e suas tecnologias; 3) Linguagens, Códigos e suas tecnologias e 4) Matemática e suas tecnologias.
Após as correções das provas, os resultados globais do Enem são amplamente divulgados pela imprensa, suas médias são comparadas com as obtidas nos anos anteriores e, consequentemente, apontam as áreas em que os estudantes foram mais bem-sucedidos.
Dados do ENEM apresentados pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep, 2019) mostram que em 2018 a média obtida pelos candidatos em cada área, em ordem decrescente, foi: Ciências Humanas - 569,2; Matemática - 535,5; Linguagens - 526,9 e Ciências da Natureza - 493,8.
Se fôssemos nos ater apenas aos números e os comparássemos com as outras áreas do conhecimento avaliadas, apesar da tão alardeada dificuldade em Matemática, sua média foi superior à de Linguagens e de Ciências da Natureza, ficando abaixo apenas de Ciências Humanas.
Outro indicador de desempenho muito utilizado é o Pisa (Programa Internacional de Avaliação de Estudantes), avaliação em larga escala aplicada a cada três anos aos estudantes na faixa dos 15 anos dos países membros e dos países parceiros da OCDE (Organização para Cooperação e Desenvolvimento Econômico). O Brasil não é membro da OCDE, mas possui o status de parceiro-chave e participa do Pisa desde sua primeira edição, no ano 2000. O Inep é o órgão responsável pela realização do Pisa no Brasil, que, além de Leitura, Matemática e Ciências, avalia também Letramento Financeiro e Competência Global.
A última edição do Pisa, que contou com a participação de 79 países, ocorreu em 2018. Diferentemente do Enem, os resultados do Pisa evidenciam o baixo desempenho dos alunos brasileiros em Matemática, os quais obtiveram pontuação média inferior à de Leitura e Ciências, áreas em que os alunos atingiram 413 e 404 pontos, respectivamente. A média de proficiência dos estudantes brasileiros em Matemática foi de 384 pontos, um valor baixo se comparado à média obtida pelos estudantes dos países membros da OCDE, que foi de 492 pontos, ou seja, uma diferença de 108 pontos. Os resultados apresentados por alunos brasileiros em Matemática também são inferiores aos daqueles de outros países da América Latina (Figura 1). Entre os países latino-americanos, o Uruguai ocupa a melhor colocação, a 58ª, ao passo que o Brasil ocupa a 70ª posição no ranking, com uma diferença de 34 pontos em relação ao país vizinho.
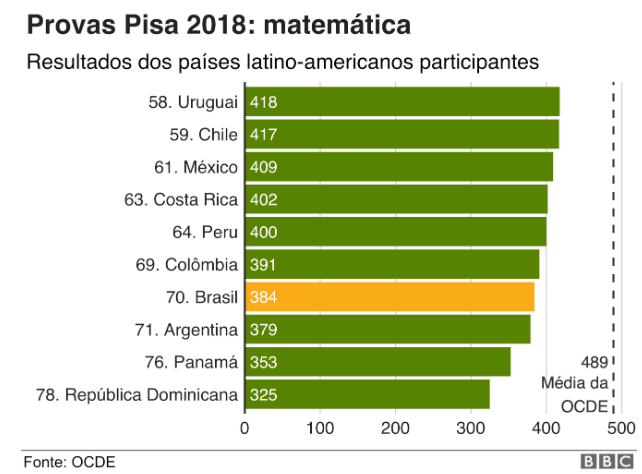
Figura 1: Resultado das provas do Pisa (Matemática 2018) dos países latino-americanos participantes
Fonte: BBC (https://www.bbc.com/portuguese/brasil-50646695).
Quando se trata da formação básica obrigatória, a Lei de Diretrizes e Bases da Educação Nacional (LDB nº 9.394/96) propõe que nossas escolas deveriam oferecer ao aluno uma formação cidadã, ou, como sugerem documentos como os Parâmetros Curriculares Nacionais (1998) e as Orientações Curriculares Nacionais (2002), tal formação deveria remeter a um ensino no qual o aluno adquirisse habilidades e competências que o auxiliassem na vida cotidiana. No que se refere ao Ensino Médio, a formação teria
como finalidades centrais não apenas a consolidação e o aprofundamento dos conhecimentos adquiridos durante o nível fundamental, no intuito de garantir a continuidade de estudos, mas também a preparação para o trabalho e para o exercício da cidadania, a formação ética, o desenvolvimento da autonomia intelectual e a compreensão dos processos produtivos (Brasil, 2006, p. 69).
Tais orientações contemplam o ensino de Matemática, que é abordado especificamente nos PCN, ressaltando-se seu “valor formativo” na estruturação do pensamento e do raciocínio dedutivo, e acrescenta que “também desempenha um papel instrumental, pois é uma ferramenta que serve para a vida cotidiana e para muitas tarefas específicas em quase todas as atividades humanas” (Brasil, 1999, p. 40).
É possível que o desempenho dos alunos brasileiros, no Enem ou no Pisa evidencie que as finalidades do ensino de Matemática previstas nos documentos oficiais não estejam sendo cumpridas na prática. Poderíamos nos basear nos resultados do Enem para simplesmente dizer que Matemática é só mais um desafio para os estudantes, já que a média obtida não foi nem a primeira e nem a última no ranking das áreas avaliadas. Se pautássemos nossa análise somente nos dados do Pisa, poderíamos chegar à conclusão de que os estudantes brasileiros, apesar de serem piores em Matemática, também não são tão bons em Leitura e Ciências, uma vez que, se compararmos a pontuação brasileira com a da China e suas províncias, primeiras no ranking, seria evidente a defasagem entre as pontuações obtidas. A pontuação obtida pelas cidades sob o domínio chinês foi de 555, 591 e 590 pontos em Leitura, Matemática e Ciências, respectivamente. Na mesma sequência, o Brasil obteve 413, 384 e 404 pontos.
Contudo, partindo para outro ponto de vista, buscamos neste trabalho deixar de lado a supremacia do que atestam os institutos avaliadores para ouvir os avaliados.
A concepção dos que passam pelo processo
É verdade que os alunos consideram a Matemática complexa ou será que o que pesa mais são as aulas pouco atrativas? Nesse sentido, autores como Resende e Mesquita (2013), entre outros, apontam para a necessidade de despertar o interesse dos alunos, ao passo que outros autores apresentam dados em que os recursos utilizados pelos professores são unicamente aulas no quadro-negro (Silva, 2013), uma situação cotidiana que segue no caminho contrário à abordagem sugerida nos PCN, em que se discorre sobre a importância da diversificação de recursos como apoio à prática pedagógica.
Aulas e livros, contudo, em nenhuma hipótese resumem a enorme diversidade de recursos didáticos, meios e estratégias que podem ser utilizados no ensino das Ciências e da Matemática. O uso dessa diversidade é de fundamental importância para o aprendizado porque tabelas, gráficos, desenhos, fotos, vídeos, câmeras, computadores e outros equipamentos não são só meios (Brasil, 1999, p. 53).
Dependendo da forma como se ensine e da maneira como se aprenda, um ou outro recurso poderá ser mais, ou menos, necessário de acordo com cada realidade. Esse é também um fator importante a se considerar quando se deseja ouvir os indivíduos envolvidos no processo, para desse modo entender as especificidades de cada grupo e quais são as suas reais necessidades diante do ensino desse conhecimento.
Quando voltamos nosso olhar para determinada escola, no sentido de sondar como seus alunos veem o ensino da Matemática, isso nos leva a “perceber também quais as concepções que a sociedade tem sobre ela” (Lopes, 2019), assim como sua função social. Resende e Mesquita (2013, p. 200) afirmam a importância de obter a visão dos alunos, ressaltando que “o diagnóstico e as concepções dos envolvidos no processo se tornam necessárias para análise e promoção de propostas de alterações”.
Dessa forma, acreditamos que tentar fazer emergir o que os alunos pensam e como se sentem é fundamental para o desenvolvimento de estratégias que sejam benéficas tanto para o aluno quanto para o professor no processo de ensino de Matemática.
O percurso da sondagem
Este trabalho foi realizado em um colégio público estadual da cidade de Nova Friburgo/RJ. O colégio oferece os turnos matutino, diurno e noturno, atendendo aos Ensinos Fundamental, Médio e Educação de Jovens e Adultos para aproximadamente 670 alunos. Ainda que precários, a escola conta com recursos como Laboratórios de Ciências e de Informática, possuindo também espaços físicos como auditório e quadra de esportes.
Com o intuito de investigar “o conhecimento de opiniões, crenças, sentimentos, interesses, expectativas, situações vivenciadas etc.” (Gil, 1999, p. 128), nosso principal instrumento na produção de dados foi um questionário estruturado composto de sete questões fechadas, anônimo, em que os participantes somente informavam seu sexo e sua idade. O questionário foi aplicado, no ano de 2019, em três turmas do turno da manhã nas quais a primeira autora do presente artigo lecionava Física. A média de idade de alunos que responderam à pesquisa foi de 16,23 anos, sendo 48% homens e 52% de mulheres, totalizando 54 alunos que cursavam o 1o e o 2o anos do Ensino Médio.
Apesar de tratarmos os dados de forma a ter um esboço quantitativo da sondagem que fizemos, nossa pesquisa foi eminentemente qualitativa. Com base nos dados produzidos, analisamos seu conteúdo à luz da literatura visitada, sem perder de vista o que nos sinalizam Gehardt e Silveira (2009, p. 3): o fato de que a pesquisa qualitativa “não se preocupa com representatividade numérica, mas, sim, com o aprofundamento da compreensão de um grupo social, de uma organização etc.”.
Esboço das percepções
Para melhor visualização dos resultados, optamos por organizar os dados que foram produzidos em gráficos de setores. Portanto, as figuras a seguir, sem indicativo de fonte, são resultado dos dados produzidos durante a pesquisa.
A primeira pergunta do questionário que propusemos aos estudantes se referia às dificuldades com a disciplina de Matemática.
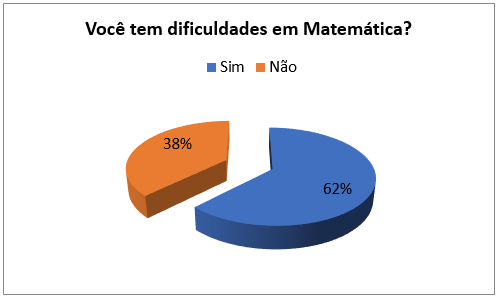
Figura 1: Você tem dificuldades em Matemática?
Os dados mostram que 62% dos participantes afirmaram ter dificuldades em Matemática, ou seja, a maior parte dos alunos. Quando separamos esses dados em relação ao gênero (Figura 2), tivemos uma outra configuração para a questão: as mulheres (89%) revelaram ter mais dificuldades em Matemática que os homens.
Em pesquisa realizada em escolas do Estado de São Paulo (Resende; Mesquita, 2013, p. 220), a maioria dos alunos, tanto de escolas públicas quanto privadas, admitiu ter dificuldade para aprender Matemática, entretanto “muitos afirmaram ter uma boa base de formação matemática, do que discordam os professores”.
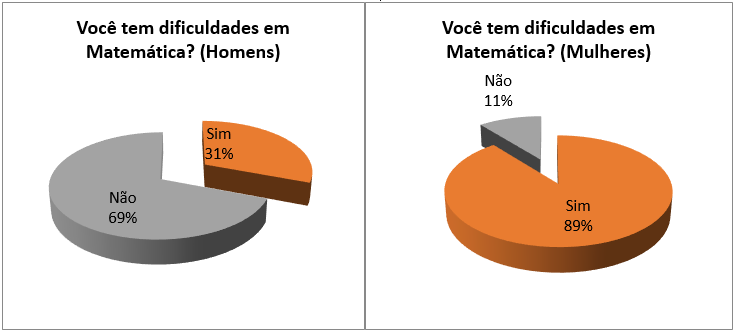
Figura 2: Você tem dificuldades em Matemática?
A impressão que os alunos teriam sobre as aulas de Matemática foi o teor da segunda pergunta do questionário (Figura 3). Uma pesquisa apresentada por Silva (2014) mostra que, além de terem dificuldade em Matemática, os alunos afirmam que as aulas são cansativas.
No estudo que realizamos, de modo geral 58% dos alunos consideraram as aulas desmotivantes (Figura 3), sendo menos atrativas para as mulheres que para os homens. As mulheres, que revelam ter dificuldades em Matemática em maior quantidade (Figura 2), são as que acham as aulas mais desmotivantes (Figura 4).
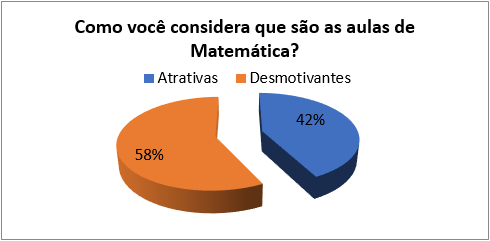
Figura 3: Como você considera que são as aulas de Matemática?
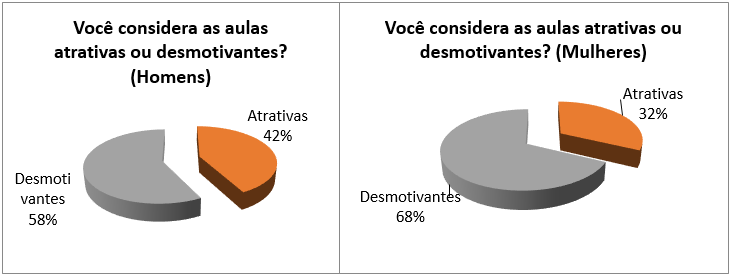
Figura 4: Como você considera que são as aulas de Matemática?
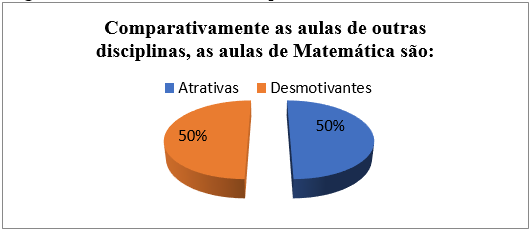
Figura 5: Comparativamente às aulas de outras disciplinas, como são as aulas de Matemática?
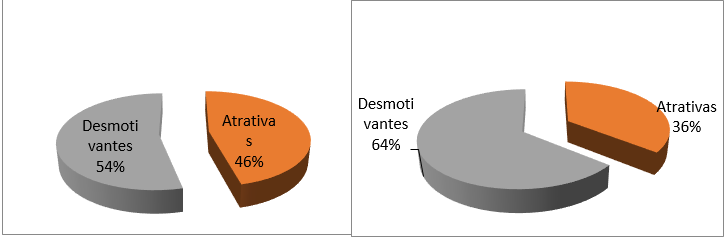
Figura 6: Comparativamente às aulas de outras disciplinas, como são as aulas de Matemática?
A terceira pergunta do questionário buscou saber o que os alunos achavam das aulas de Matemática em comparação com outras disciplinas (Figura 5). Os participantes se dividiram ao fazer a comparação, mostrando que as outras disciplinas não são expressivamente mais atrativas que Matemática. Em relação ao gênero, os dados mostraram mais uma vez o quanto as aulas de Matemática são desmotivadoras para as mulheres, inclusive mais que as aulas de outras disciplinas (Figura 6).
Ao serem perguntados, na quarta questão, sobre a qualidade das aulas (Figura 7), 72% dos respondentes apontaram as aulas do Ensino Médio como melhores que as do Ensino Fundamental. Ao separarmos os grupos, tanto os homens quanto as mulheres afirmaram que as aulas diferem em qualidade, porém os homens (73%) em maior número (Figura 8).
É importante ressaltar aqui que, durante a aplicação do questionário, foram esclarecidas as intenções de cada pergunta e os alunos também poderiam tirar dúvidas quanto à sua interpretação. Nesta quarta questão foi elucidado que nossa intenção era saber se para eles as aulas do Ensino Médio teriam qualidade superior que as do Ensino Fundamental.
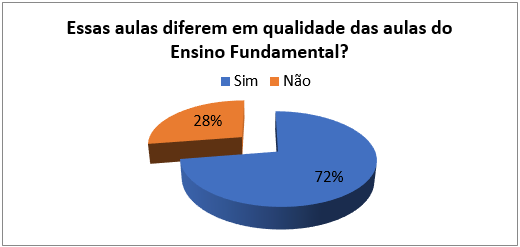
Figura 7: Essas aulas diferem em qualidade das aulas do Ensino Fundamental?
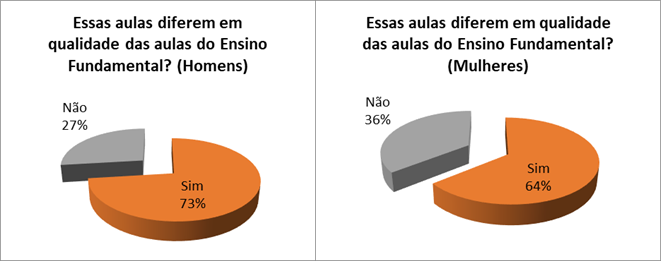
Figura 8: Essas aulas diferem em qualidade das aulas do Ensino Fundamental?
Na quinta questão, os participantes foram consultados sobre a importância do conhecimento matemático. Nesse contexto que aponta fatores negativos em relação ao ensino de Matemática, eles consideraram, em sua maioria (85%), que o conhecimento matemático era importante (Figura 9). Percepção semelhante à encontrada por Resende e Mesquita (2013, p. 220) na pesquisa feita nas escolas de São Paulo, em que “muitos alunos admitiram a importância do estudo da Matemática, não só na escola, como no seu cotidiano, e admitiram seu interesse em frequentar aulas extras, se lhes fossem oferecidas”.
No nosso estudo, o que chamou especialmente nossa atenção foi o grupo de mulheres que declarou ter dificuldade (Figura 2) e que não se sentiam motivadas pelas aulas ministradas (Figura 4), mas que consideraram, em sua totalidade (100%), o conhecimento matemático como importante (Figura 10).
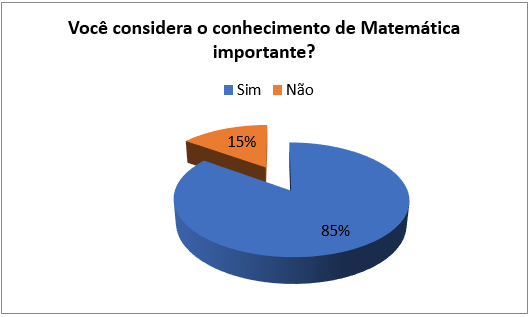
Figura 9: Você considera o conhecimento de Matemática importante?
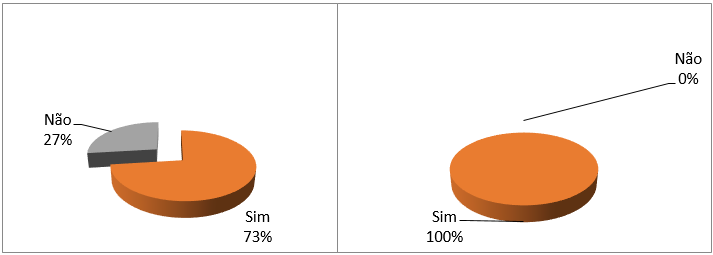
Figura 10: Você considera o conhecimento de Matemática importante?
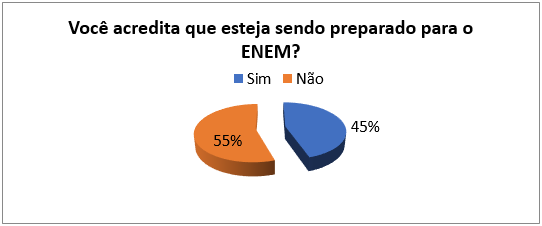
Figura 11: Você acredita que esteja sendo preparado para o Enem?
Em relação ao Enem, como se sentem os alunos? A sexta pergunta do nosso questionário de pesquisa mostrou que 55% dos alunos não se sentem preparados para realizar o exame (Figura 11). Apesar de alegarem menores dificuldades em relação às mulheres (Figura 2), os homens se sentem sensivelmente mais despreparados para o exame em comparação com elas (Figura 12).
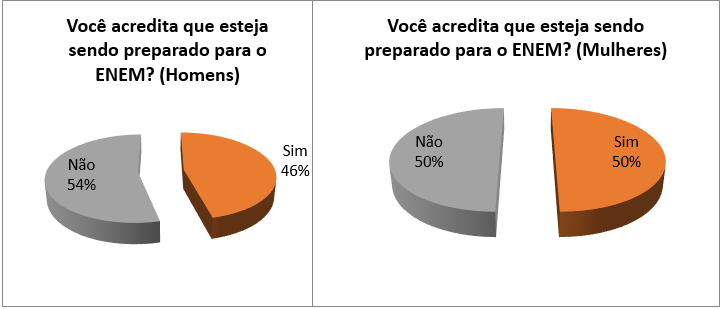
Figura 12: Você acredita que esteja sendo preparado para o Enem?
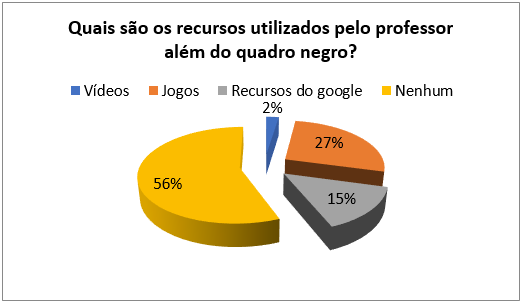
Figura 13: Quais são os recursos utilizados pelos professores além do quadro-negro?
Finalizamos o questionário com uma tentativa de investigar os recursos utilizados em sala de aula; 56% dos alunos afirmaram que seus professores não utilizavam, no decorrer das aulas, nenhum outro recurso que não fosse o quadro-negro (Figura 13), o que ratifica a tendência revelada por Silva (2014) de que as “metodologias predominantes nas aulas de Matemática ainda são as consideradas tradicionais” e contraria o que a Unesco aponta como ideal para educação no século XXI, que é a escola colaborando para que os alunos aprendam a aprender e aprendam a fazer (Delors, 1999).
Em nosso questionário fechado, só havia três opções de resposta: vídeos, jogos e recursos do Google. É interessante destacar que os alunos participantes é que incluíram a quarta opção nenhum, para poder expressar que seus professores não utilizavam nenhuma das opções de resposta propostas por nós.
Possíveis percursos nas entrelinhas
Em Educação Matemática padecemos da indefinição de um arcabouço conceitual sobre o qual poderíamos basear nossas análises (Skovsmose, 2014, p. 25). Uma indefinição, segundo Skovsmose, que quando a descreve o faz referindo-se “às grandes incertezas relativas às funções que a Educação Matemática pode exercer nos diversos contextos sociopolíticos” (Skovsmose, 2014, p. 25).
Dada essa indefinição, fizemos a opção de olhar para os dados aqui produzidos a partir do modo como a Matemática pode potencializar ou despotencializar os alunos (Skovsmose, 2014, p. 15-23) e buscando refletir sobre as ideias envolvidas nesses conceitos que poderiam influenciar suas percepções, sem ignorar, contudo, as relações de gênero envolvidas e os traços de colonialidade que perpassam a admitida dificuldade em Matemática, a função social da posse desse conhecimento e o modo como esse saber é apresentado e trabalhado em sala de aula.
Ao considerarmos uma escola que privilegia o ensino tradicional, não raramente encontramos nesse ambiente o paradigma do exercício e a ideologia da certeza (Skovsmose, 2014) ocupando lugares de honra nas práticas cotidianas das aulas tradicionais. Muito familiar para milhões de alunos que frequentaram as escolas brasileiras, o paradigma do exercício é facilmente reconhecido em função da organização das aulas e dos padrões de comunicação existentes, em que
o comum é que as aulas contenham exposições orais do professor feitas em função de materiais didáticos elaborados por agentes externos àquele ambiente de aprendizagem. O cenário tradicional que se instaura no paradigma do exercício é o de alunos que devem resolver exercícios e outras atividades, que em geral admitem uma, e somente uma, resposta correta. As aulas expositivas são essenciais para a apresentação e desenvolvimento dos conteúdos, das ideias, dos conceitos e das técnicas necessários ao bom desempenho na resolução dos exercícios escolhidos pelo professor ou prescritos pela instituição ou rede de ensino (Lima, 2016, p. 52).
Partindo de nossas próprias experiências como alunos, ousamos dizer que passamos a maior parte de nossas vidas escolares resolvendo centenas de exercícios do tipo “Encontre o valor de x”, “Resolva”, “Calcule”, “Arme e efetue”... entre tantos outros que diziam respeito somente à aplicação de conceitos e técnicas que envolviam saberes da Matemática pura (Skovsmose, 2014, p. 18 e 54). Quando não era dessa forma, quase todos tínhamos problemas contextualizados que se referiam ao recorte de uma realidade muitas vezes distorcida para caber numa situação passível de ser matematizada. Como seria o caso de propor em um problema que uma criança fosse ao mercado comprar uma quantidade absurda de melões somente para que o aluno fizesse determinada conta e encontrasse certo resultado que satisfizesse a aplicação de alguma técnica relacionada ao conteúdo que estivesse sendo trabalhado (Figura 14).

Figura 14: Semirrealidade
Fonte: https://www.facebook.com/spigmath/
Tais exercícios são classificados por Skovsmose como artificiais e situados dentro de uma semirrealidade. Segundo o autor, é “bem possível que as referências a essa semirrealidade ajudem os alunos a contextualizar seus procedimentos matemáticos” (2014, p. 55), porém faz o alerta de que uma semirrealidade “funciona como um mundo platônico em que toda a informação é exata e verdadeira” (Skovsmose, 2014, p. 55). São atividades que se referem a algo que de fato existe ou que é muito próximo da realidade, mas temos que admitir que uma semirrealidade não é a realidade. Os estudantes são submetidos, ao longo dos anos de escolaridade, a um aglomerado de tarefas muitas vezes extenuantes, que não lhes interpõem desafios reais nem contribuem para desenvolver a criatividade ou uma visão crítica do mundo em que se encontram.
O paradigma do exercício vem também permeado pela ideologia da certeza, a ideia de que a Matemática traz em si uma garantia de solidez e exatidão em seus resultados.
A ideologia da certeza ostenta a ideia de que todo tipo de situação pode ser matematizada e de que a Matemática não seria suscetível às diversas influências externas de cunho social ou político, ou mesmo ideológico, conferindo-lhe a garantia de uma ciência livre da intervenção humana. Fazendo com que seja esquecido o fato de que se exigem recortes e a necessidade de conformação de uma situação a um contexto adequado à proposta de matematização. E sabemos que é assim, à base de ajustes, que é criada uma infinidade de problemas matemáticos apresentados aos nossos alunos (Lima, 2016, p. 52-53).
Quase sempre são propostas situações herméticas e prontas, emergindo daí um “micromundo em que todas as medidas são exatas, e os dados fornecidos são necessários e suficientes para a obtenção da única e absoluta resposta certa” (Lima, 2016, p. 17), propostas essas que não requerem que os alunos busquem mais informações e influências reais que poderiam contribuir para diversas soluções possíveis para uma mesma situação, já que “toda a informação está à disposição, e os alunos podem permanecer quietos em suas carteiras resolvendo exercícios” (Lima, 2016, p. 17), ou seja, algo muito prático e cômodo. A quem interessa essa praticidade e comodidade? Que tipo de contribuições trazem aos alunos? Ou, como se pergunta Skovsmose: “será que o ensino de Matemática tradicional contribui para embutir nos alunos uma obediência cega que os habilita a participar de processos de produção em que a execução de ordens sem questionamento é um requisito essencial?” (2014, p. 18-19).
Um dos grandes problemas com esse modelo é que quem não se adéqua a ele é que se constitui em um problema. Já que prepara alunos que alcançam índices de aprovação nos exames internos e externos às instituições educacionais, esse é um modelo aceito como eficaz, nem sempre questionado por muitos pais, alunos, professores e governos. Pelo contrário: é um modelo exaltado que traz em si uma ideia recorrente de que só não se adaptam os incapazes. É senso comum: aquele que sabe Matemática é inteligente e tem mais chances de sucesso na vida. Esses rótulos não beneficiam os alunos como um todo e fazem com que, como afirmam Healy e Powell (2013), sejam evitadas as reflexões a respeito do currículo de Matemática e sobre como ele é oferecido nas escolas, na medida em que os estudantes com baixa escolaridade é que são o problema, o que nos leva a refletir sobre se o alto índice de dificuldade em Matemática na pesquisa que aqui apresentamos é o reconhecimento de diferenças pessoais ou o resultado de condições desvantajosas de aprendizagem.
A admissão da dificuldade vem acompanhada de um instantâneo de como são vistas as aulas das quais eles mesmos participam e do lugar que esse conhecimento ocupa no imaginário do grupo. De fato, é a “rainha das ciências” (título atribuído por Carl Friedrich Gauss (1777-1855)), principalmente para as mulheres. Uma rainha inatingível que concede audiência para uns poucos escolhidos e que teria preferência por homens, na medida em que historicamente as mulheres tiveram pouco espaço e muitos dos seus rastros de contribuição ao saber matemático só recentemente têm sido reconstruídos. Por muito tempo, Matemática foi considerada coisa só de homem; atualmente ainda percebemos a força desse discurso.
Nossa pesquisa pode remeter ao que Souza e Fonseca (2015) concluem em sua investigação sobre configurações das relações de gênero nas práticas matemáticas em uma associação de catadores de materiais recicláveis que participavam de um projeto de Educação de Pessoas Jovens e Adultas (EJA). As pesquisadoras refletiram sobre os discursos que permeiam as relações entre esses personagens, homens e mulheres entre 18 e 76 anos, em sala de aula.
Apesar de todas as que responderam ao nosso questionário considerarem a Matemática um conhecimento importante (Figura 10), não parece ser um assunto que lhes seja acessível, em função da declarada dificuldade informada por elas (Figura 2). Tal evidência, assim como em Souza e Fonseca (2015, p. 274), faz refletir
sobre o espaço escolar como um espaço no qual se produzem identidades hegemônicas de gênero e práticas matemáticas também tornadas hegemônicas em nossa sociedade. É no espaço da escola – e pelo aparato discursivo que nela circula, que ela produz e nela se (re)produz – que a Matemática é constantemente fabricada como um reduto masculino, ao mesmo tempo que se fabricam como naturais: a razão como posse do homem; e a falha, a dificuldade ou a dedicação (em geral inglória) frente a essa Matemática como inerente à condição feminina.
As jovens que participaram de nossa pesquisa parecem assumir como legítimo o discurso de que mulheres não são tão capazes quanto homens para o aprendizado de Matemática e dessa forma expõem com mais espontaneidade suas dificuldades e falta de motivação, admitindo como real o ficcional “discurso conservador machista que produz as mulheres como cordatas, solidárias, cumpridoras de normas e regras, adaptáveis; e os homens como atirados, transgressores, indomáveis” (Souza; Fonseca, 2015, p. 274). Esse tipo de discurso, também presente no espaço escolar, faz com que as mulheres se coloquem em segundo plano, como coadjuvantes de um jogo que costuma ter como natural esperar que elas não participem dele como protagonistas. Em vez disso, “esse discurso autoriza e legitima que os homens mostrem como jogam esse jogo, valorizando sua destreza ao jogá-lo e se posicionando, nesse jogo, como bons em Matemática”(Souza; Fonseca, 2015, p. 274).
Entretanto, de modo geral, os resultados dessa pesquisa trazem o reflexo do senso comum, quando tornam evidente o que já se intuía: a dificuldade em uma disciplina que é amplamente aceita como difícil. As percepções dos estudantes a respeito das aulas e dos recursos utilizados não determinam, mas denunciam a conformação de uma escola em que o que se pratica tem características do paradigma do exercício e da ideologia da certeza. E, apesar de admitirem receber um ensino de qualidade superior ao que tiveram no Ensino Fundamental, os alunos não se sentem seguros para enfrentar um exame que poderá repercutir em suas vidas futuramente – nesse caso, o Enem.
Evidencia-se assim, um formato de escola que não é exceção, mas que ainda é recorrente em nossos territórios e mantém-se distante dos anseios daqueles a quem deveria atender. Como afirma Freire (1996, p. 46), “o desrespeito à leitura de mundo do educando revela o gosto elitista, portanto antidemocrático, do educador, que dessa forma, não escutando o educando, com ele não fala. Nele deposita seus comunicados”. A Pedagogia bancária de Freire reflete também as consequências de um processo formal de colonização política e territorial sofrida pelo povo brasileiro durante mais de três séculos. O período de colonização portuguesa se encerrou, mas ainda permanece a colonialidade, ou seja, padrões de poder resultantes desse colonialismo. A colonialidade se traduz em várias formas de dominação, históricas e contemporâneas, e se faz presente em muitas de nossas estruturas e relações sociais, culturais, políticas e econômicas.
A escola é uma dessas instituições em que podemos identificar o pensamento colonial, quando nós, como professores, desqualificamos o saber do aluno ou quando olhamos para suas diferenças como se fossem deficiências (Healy; Powell, 2013), de modo que nossas salas de aula acabam por serem permeadas por essas relações de colonialidade. Do ponto de vista macro, a presença tácita da colonialidade no ensino de Matemática no Brasil se comprova pela ausência de referências culturais e pessoais oriundas de matrizes africanas e indígenas, que não são reconhecidas nem legitimadas como saber integrante da cultura brasileira.
As contribuições e os modos de pensar matematicamente dos povos indígenas e africanos são desconsiderados frente ao acúmulo do saber matemático de origem eurocêntrica. Este é um dos exercícios que somos chamados a fazer como professores: deslocar a produção matemática desses povos do lugar do atraso em relação à produção matemática eurocêntrica, dissolvendo a estrutura que hierarquiza uma produção em relação à outra e, com isso, criarmos condições mais próprias e próximas de nossa cultura e da dos educandos.
Não significa que deixaremos de nos aprofundar ou que ignoraremos a Matemática contemporânea, mas daremos a cada produção o seu reconhecimento e lugar político por meio de nossa atuação como docentes.
Quando o erro, a falta de entendimento ou a dificuldade dos nossos alunos são colocados pelo olhar colonial no lugar do atraso e da falta de capacidade, deixamos de nos abrir a outros entendimentos e a uma variedade de possibilidades de produção do conhecimento matemático. Talvez um dos principais fatores de fracasso de nossos jovens nas temidas avaliações e concursos seja o fato de estarem imersos em condições de aprendizagem que lhes sejam desfavoráveis e de serem continuamente despotencializados diante desse conhecimento, seja por questões sociais, de gênero, de raça ou culturais, em vez de serem estimulados a desenvolver suas potencialidades de produção do pensamento matemático no espaço escolar.
Considerações finais
De acordo com a pesquisa realizada, é clara a sensação de dificuldade da maioria dos alunos com a disciplina. Analisando-a em relação ao gênero, essa sensação é ainda mais acentuada nas mulheres, porém seria importante verificar melhor o que ocorre, e essa é uma das perspectivas para este trabalho, principalmente buscando gerar reflexões que tornem evidente a existência desses discursos conservadores que delimitam o papel de homens e mulheres nas práticas educacionais cotidianas, no sentido de contribuir para a redução dessa desigualdade.
Já que os alunos aprendem de diferentes modos, diferentes recursos deveriam ser utilizados. A falta de utilização de recursos diversificados é um agravante para uma disciplina que é comumente considerada excludente. A pesquisa aponta para uma situação na qual os professores não utilizam variados recursos importantes para educação dos alunos, o que poderia favorecer todos os envolvidos no contexto de aprendizagem, se levarmos em conta que cada pessoa aprende de uma maneira diferente.
Os dados apresentados indicam que a forma como se ensina Matemática no Ensino Médio precisa sofrer intervenções sob vários aspectos, mas, no que tange ao papel do professor, somos levados a considerar a possiblidade de desconstruir pensamentos e posturas enraizados na prática docente e que possam fazer com que nossos alunos não se sintam capazes de aprender e produzir Matemática.
Diante do que expusemos aqui, seria muito fácil trilhar o caminho da culpabilização. Entretanto, não é essa a nossa proposta, mas trazer elementos que possam ajudar a refletir sobre a nossa prática como professores. Em momento algum é possível desconsiderar as péssimas condições de trabalho dos professores que atendem à maior parte da população, assim como os baixos salários auferidos pela categoria, que impõem a ela uma jornada de trabalho exaustiva e desumana.
Certamente não mudaremos o sistema da noite para o dia nem conseguiremos mudar a rotina de estudos, atender cada especificidade de nossos alunos ou mesmo satisfazer suas diferentes condições de aprendizagem. A despeito de todos os obstáculos e de nossas limitações, somos nós, professores, que atuamos no cotidiano das salas de aula. A pergunta que fica é: o que podemos mudar, em nossa prática, para mitigar os problemas e fazer com que nos aproximemos das pessoas para e com quem trabalhamos de modo a desconstruir paradigmas, rótulos e condições de aprendizagem que despotencializem e desfavoreçam tantos estudantes que são mantidos à margem do saber matemático.
Ao deixarmos de enxergar o conhecimento matemático como produto da genialidade, é possível que possamos começar a abandonar o exercício do papel do professor como classificador, que separa os bons dos ruins, colocando muitos alunos no lugar do atraso, rotulando-os como deficientes, inábeis ou incompetentes. Certamente nos cabe fazer o exercício de tirar nossos alunos do lugar do atraso e lhes acenar com a possibilidade de reconhecer seu lugar político de atuação, de resistência e de produção de conhecimento. Tal mudança de postura é uma das contribuições que poderão provocar mudanças nas relações de poder que se perpetuam em nosso sistema de ensino.
Nossa pesquisa foi uma tentativa de ouvir os alunos que estão inseridos no processo de aprendizagem e refletir a respeito de suas percepções, buscando entender de que forma elas podem nos ajudar a romper com modelos que excluam indivíduos e não contribuam para que o conhecimento matemático seja de fato compreendido, respeitando a diversidade e as peculiaridades de cada indivíduo.
Referências
BRASIL. MEC. Parâmetros Curriculares Nacionais. Brasília: MEC, 1999.
______. Orientações Curriculares Nacionais. Brasília: MEC, 2006.
DELORS, J. Educação: um tesouro a construir. Relatório da Comissão Internacional sobre Educação para o Século XXI. 2010. Disponível em: http://unesdoc.unesco.org/images/0010/001095/109590por.pdf. Acesso em: 7 mar.2018.
FREIRE, P. Pedagogia da autonomia: saberes necessários à prática educativa. São Paulo: Paz e Terra, 1996. (Coleção Leitura).
GERHARDT, T.; SILVEIRA, D. T. Métodos de pesquisa. Porto Alegre: Editora da UFRGS, 2009. Disponível em: http://www.ufrgs.br/cursopgdr/downloadsSerie/derad005.pdf.
HEALY, L.; POWELL, A. Understanding and overcoming “disadvantage” in learning Mathematics. In: CLEMENTS, M. A. (Ken) et al. (Eds.). Third International Handbook of Mathematics Education, p. 69-100, 2013.
GIL, A. C. Métodos e técnicas de pesquisa social. 5ª ed. São Paulo: Atlas, 1999.
INSTITUTO NACIONAL DE ESTUDOS E PESQUISAS EDUCACIONAIS ANÍSIO TEIXEIRA (INEP). Relatório Brasil no Pisa 2018 – versão preliminar. Brasília: MEC/Inep, 2019. Disponível em: http://download.inep.gov.br/acoes_internacionais/pisa/documentos/2019/relatorio_PISA_2018_preliminar.pdf. Acesso em: 11 jan. 2019.
LIMA, A. S. Educação Financeira no Ensino Fundamental: um bom negócio. Dissertação (Mestrado), Colégio Pedro II, Câmpus São Cristóvão, Rio de Janeiro, 2016.
LOPES, N. S. O.; SANTOS, E. B.; DIAS, G. F. A. Concepções de Matemática: Olhar dos estudantes do Ensino Médio. Disponível em: http://editorarealize.com.br/revistas/epbem/trabalhos/Comunicacao_385.pdf. Acesso em: 15 dez. 2019.
RESENDE, G.; MESQUITA, M. G. Principais dificuldades percebidas no processo ensino-aprendizagem de Matemática em escolas do município de Divinópolis/MG. Educação Matemática Pesquisa, São Paulo, v. 15, nº 1, p.199-222, 2013. Disponível em: https://revistas.pucsp.br/emp/article/view/9841. Acesso em: 10 dez. 2019.
SKOVSMOSE, O. Um convite à Educação Matemática Crítica. Campinas: Papirus, 2014.
SOUZA, M. C. R. F.; FONSECA, F. R. Relações de gênero e Matemáticas: entre fios e tramas discursivas. Educar em Revista, Curitiba, nº 55, p. 261-276, jan./mar. 2015.
Publicado em 28 de julho de 2020
Como citar este artigo (ABNT)
BERNARDES, Adriana Oliveira; LIMA, Adriana de Souza; GIRALDO, Victor. A percepção dos alunos de Ensino Médio de uma escola pública sobre o ensino de Matemática. Revista Educação Pública, v. 20, nº 28, 28 de julho de 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/28/a-percepcao-dos-alunos-de-ensino-medio-de-uma-escola-publica-sobre-o-ensino-de-matematica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

