Um caminho para o cálculo: o ensino da matemática na perspectiva das investigações
Emily Bomfim Souza
Licencianda do curso de Pedagogia (UPM-SP), auxiliar de professor da rede pública (SP)
Sônia Cha Kim
Licencianda do curso de Pedagogia (UPM-SP)
Este artigo destina-se a refletir sobre a prática docente do ponto de vista do ensino da Matemática, intrinsecamente o caminho percorrido pelo aluno até a chegada do cálculo, atingindo o algoritmo convencional na forma de conta armada. Não obstante, este trabalho traz juntamente propostas de atividades voltadas ao ensino do cálculo com base teórica apoiada nas investigações matemáticas discorridas por Ponte; Brocardo e Oliveira (2003).
O conteúdo a ser apresentado busca revelar brevemente duas perspectivas, a contagem e o cálculo, e como elas estão relacionadas no aprendizado dos números. O trabalho divide-se, além da introdução, em outras duas seções. A seção seguinte destina-se a refletir sobre a teoria e a prática pedagógicas relativas à construção de relações matemáticas até a chegada do cálculo, buscando trazer reflexões sobre a possibilidade de adotar aulas investigativas na prática pedagógica de Matemática. Encerrando o artigo, as considerações finais revelam como a ação docente pode ser refletida do ponto de vista significativo nas investigações matemáticas para a aprendizagem do cálculo.
O processo de aprendizagem dos números pela criança
É notório que aprender sobre números demanda uma longa trajetória no processo de aprendizagem do sujeito educando. Nesse contexto, faz-se necessário compreender a princípio como se dá propriamente o conhecimento humano. Para apoiar esta investigação, torna-se possível aludir às ideias teóricas do biólogo Piaget, que considera a existência de três tipos de conhecimento: físico, social e lógico-matemático. O conhecimento físico corresponde a uma fonte externa ao sujeito, estando presente parcialmente no objeto (peça, cor, tamanho e outros); no caso desse conhecimento uma porta de entrada seriam os cinco sentidos. O conhecimento social é também conhecido como conhecimento convencionado ou cultural, parcialmente presente em convenções transmitidas de gerações em gerações, como nomes, datas comemorativas e outros. Por outro lado, o conhecimento lógico-matemático é uma fonte interna (de dentro para fora) do indivíduo, que faz parte tanto do conhecimento físico quanto do social, uma vez que parte das relações criadas pelo sujeito com o ambiente (Kamii, 2002).
Nesse contexto, torna-se válido salientar que a criança constrói o conhecimento lógico-matemático por meio das diversas relações que estabelece, e uma dessas relações possíveis recai sobre a construção do conceito de número, que é propriamente uma relação criada mentalmente (internamente) por cada criança de modo natural, através das relações estabelecidas com o meio, com o mediador e seus pares, envolvendo juntamente o amadurecimento biológico e as experiências vividas, o que leva a estabelecer variadas relações que favorecem essa construção, que tem como porta de entrada a contagem (aplicação do conceito de número), que, por sua vez, é uma construção resultante de duas relações: ordem/organização e inclusão hierárquica, como corrobora Kamii: “Piaget foi adiante para explicar que o desenvolvimento de conceitos numéricos resulta da síntese de dois tipos de relações: inclusão hierárquica e ordem” (2002, p. 22).
Nesse sentido, existem duas estruturas cognitivas importantes para o desenvolvimento da contagem: classificação e seriação. A seriação (organizar, ordenar) e a classificação (separar pelos parecidos) não se aplicam diretamente na construção do conceito de número, pois, para serem entendidas como partes fundantes do pensamento lógico-matemático, essas estruturas cognitivas do pensamento devem ser colocadas em prática por meio de situações de contagem; de todo modo, não é porque estão prontas que as estruturas serão colocadas em ação pelo sujeito.
Assim, torna-se importante que o docente compreenda que a construção do conceito de número não pode ser ensinada, pois é da própria criança; entretanto, cabe ao mediador proporcionar ao educando situações lógico-matemáticas que favoreçam as relações de contagem, pois nessas situações as crianças irão precisar tomar duas providências principais: organizar e incluir, e para organizar elas colocarão em ação a estrutura interna do pensamento que veio da seriação, em uma ideia de contar um mesmo objeto apenas uma vez. “A única forma de podermos ter certeza de que não esquecemos nenhum ou contamos o mesmo objeto mais de uma vez é colocando-os em uma relação de ordem” (Kamii, 2002, p. 24). Por outro lado, para a inclusão hierárquica (incluir mentalmente “três” em “quatro”; “cinco” em “seis” e assim sucessivamente), a criança coloca em ação a estrutura cognitiva de classificação para conseguir incluir as quantidades umas dentro das outras, realizando um esforço mental para dividir o todo em partes e juntar as partes no todo (reversibilidade), como reiteram Kamii e Housman.
Para quantificar um conjunto de objetos numericamente, a criança deve colocá-los em uma relação de inclusão hierárquica [...]; por volta dos sete a oito anos de idade, o pensamento da maioria das crianças torna-se suficientemente móvel para ser reversível. Reversibilidade refere-se à capacidade de realizar mentalmente duas ações opostas simultaneamente – neste caso, dividir o todo em duas partes e reunir as partes em um todo (Kamii; Housman, 2002, p. 23-24).
Como resultado das relações das estruturas mentais (inclusão e ordenação), espera-se a construção gradual da estrutura mental de conservação de números; “refere-se à nossa capacidade de deduzir, por meio de raciocínio lógico-matemático, que a quantidade de uma coleção permanece a mesma quando seu arranjo espacial e sua aparência empírica são alterados” (Kamii; Housman, 2002, p. 18).
Transpondo as ideias discutidas para um viés pedagógico, torna-se possível inferir que existem diversas situações escolares em que o docente pode utilizar para estimular o pensamento numérico das crianças. Dentre eles, a própria arrumação da sala de aula pode se configurar como espaço aritmizador, por meio de informações numéricas, como: calendário, relógio, quadro numérico e outros, estimular a construção numérica em atividades lúdicas, como as cantigas que envolvam ideias de quantificação, os mercadinhos com uso de cédulas para verificar as ideias de conservação numérica e outros. As atividades com jogos, principalmente as que proporcionem a participação em grupo, podem favorecer muito a troca de ideias frente ao raciocínio tido pela criança.
Outra estratégia muito enriquecedora é a utilização das coleções de objetos, que favorecem situações de contagem, desvelando a construção da criança em relação a ordenação e inclusão, o que favorece a construção do conceito de número. Assim, é importante que a escola, intrinsecamente o mediador, oferte estímulos que respeitem a autonomia do aluno e seu processo de construção de conhecimento, proponha problemas, adote uma postura de curiosidade sobre os alunos, compreendendo como brincam e como interagem, na tentativa de arriscar com novas propostas de atividade que ofertem um espaço convidativo e que favoreçam a construção de diversas relações, o que por sua vez favorece a construção de saberes diversos, sendo um deles os conceitos numéricos.
Piaget e Szeminska (1964 apud Kamii e Housman, 2002, p. 27) apontam que “os conhecimentos numéricos parecem ser construídos progressivamente, primeiro até aproximadamente sete, então até mais ou menos quinze, e mais tarde até aproximadamente 30”. Nesse contexto, entende-se que a construção do conhecimento numérico se dá para o sujeito em processos ao longo da vida, e uma das possibilidades para trabalhar o avanço dessa construção é estimular nas crianças outras possibilidades de contagem que possuam como porta de entrada o agrupamento, que se torna um fundamental passo para que as crianças comecem a contar de outras formas, que vão além do 1 em 1 (que é uma forma confortável de contar, mas não será eficiente a longo prazo para os desafios que vêm pela frente).
Na prática, o professor pode propor para as crianças coleções maiores do que aquelas a que estão acostumadas para causar um desequilíbrio e/ou desconforto mental que venha a desvelar a necessidade de fazer agrupamentos; pedir para os educandos contarem de outras formas que não seja de 1 em 1 é uma ação intencional pedagógica para levar as crianças a avançar para agrupamentos de 10 em 10. O desenvolvimento do agrupamento de base 10 é uma abertura muito importante para a criança ampliar sua compreensão sobre o sistema de numeração decimal (SND).
Sabe-se que a criança, mesmo antes de adentrar a escolarização, já convive em diferentes contextos com o sistema de numeração, como colocado por Lerner e Sadovsky (1996, p. 74-75):
as crianças têm oportunidade de elaborar conhecimentos acerca desse sistema de representação muito antes de ingressar na primeira série. Produto cultural, objeto de uso social cotidiano, o sistema de numeração se oferece à indagação infantil desde as páginas dos livros, a listagem de preços, os calendários, as regras, as notas da padaria, os endereços das casas...
Como citado pelas autoras, mesmo antes de compreender as regularidades e a lógica estrutural do sistema numérico, as crianças já possuem a capacidade de raciocinar sobre ele. É notório que os números estão expostos no cotidiano; entretanto, torna-se indispensável que sejam proporcionados ao educando o contato e a exploração das propriedades específicas do sistema de numeração decimal (SND). Nesse contexto, as pesquisas realizadas por Lerner e Sadovsky (1996) apoiam a compreensão de como as crianças constroem hipóteses para escrever os números, no intuito de evidenciar como a criança pensa que escreve o número escrevendo propriamente o número. O estudo das autoras pauta-se em dois principais eixos: escrita e comparação de números e o eixo das operações.
Ao focar no eixo da escrita e comparação de números, algumas hipóteses feitas pelas crianças são percebidas em situações intencionais de comparação entre os números. Quando questionadas sobre qual número é maior, as crianças levantam a hipótese de que “quanto mais algarismos maior é o número” e “o primeiro algarismo é quem manda”; nessas hipóteses percebe-se que, mesmo antes de as crianças dominarem a escrita convencional dos números, já consideram estratégias e relações necessárias para diferenciar os números vistos como maiores e menores. Nessa mesma pesquisa, outra hipótese foi levantada pelas crianças: “escrever como falo”; nesse sentido, “as crianças elaboram conceitualizações a respeito da escrita dos números, baseando-se nas informações que extraem da numeração falada e em seu conhecimento da escrita convencional dos nós” (Lerner e Sadovsky, 1996, p. 92); por exemplo, ao representar o número 23, podem escrevê-lo 203, uma vez que a criança escreve o número apoiada na numeração falada, o que gera a elaboração de uma representação escrita aditiva e não convencional; porém, ao deparar-se com essa escrita não convencional, acabam entrando em conflito, o que pode levar à elaboração de estratégias para possíveis correções da escrita, como apontado por Lerner e Sadovsky (1996, p. 108),
em síntese, as escritas que correspondem à numeração falada entram em contradição com as hipóteses vinculadas à quantidade de algarismos das notações numéricas. Tomar consciência desse conflito e elaborar ferramentas para superá-lo parecem ser passos necessários para progredir até a notação convencional.
Essa pesquisa mostra a importância de apresentar as regularidades do sistema, para que o educando possa levantar estratégias que o façam compreender as regras do sistema de numeração. Trazendo essas questões para um viés prático pedagógico, uma proposta para o eixo da escrita e comparação de números pode ser o ditado numérico, que, por sua vez, favorece a escrita do número, que a princípio pode ser híbrida e não convencional, mas conforme escreve pode gerar insatisfação diante do número escrito, o que leva o aluno a buscar novas formas de representá-lo. Essa percepção frente à própria escrita pode ser proporcionada justamente pelo uso do quadro numérico de base 10, pois esse recurso proveniente do conhecimento físico e social traz regularidades do sistema numérico, e a partir da observação dessas regularidades torna-se possível fazer generalizações, ou seja, espera-se que o aluno seja capaz, a partir de certo exemplo, de transpor a regularidade para novas situações, com novos desafios, de forma que consiga em alguma medida generalizar. Vale lembrar que são características do sistema de numeração decimal (base 10): a cada 10 elementos de uma natureza, se tem outra natureza; a cada 10 unidades tem-se 1 dezena, a cada 10 dezenas 1 centena, a cada 10 centenas 1 milhar, e assim sucessivamente, aliado à questão da posicionalidade – quando o número ocupa determinado lugar na escrita ele deve ser multiplicado pela sua base, então aquele que se encontra na ordem da dezena deve ser multiplicado por 10, na ordem da centena por 100, e assim por diante; função do zero: vazio e marca de posição – 01 unidade (vazio) 10 (e marca de posição).
Outra estratégia muito enriquecedora que pode ser utilizada desde o início do processo de contagem até um longo período na aquisição dos conhecimentos numéricos é a utilização das coleções. Propor que as crianças façam uma coleção, como de pedras ou tampinhas de garrafa, e solicitar que contem essas coleções e, conforme a coleção vai crescendo, anotem os números que correspondem à coleção favorece que a criança perceba a facilidade que esse registro pode promover para seu cotidiano.
Partindo do pressuposto de que não existe “fórmula mágica” para estimular as crianças frente aos conhecimentos numéricos, faz-se importante que o docente paute sua ação em questionar e provocar os alunos por meio de atividades de comparação numérica, com recursos lúdicos, como jogos e brincadeiras, traga questões que causem interesse em investigar, como: números das casas, número dos calçados, peso, idade, datas comemorativas, números de peças da coleção que estão montando, números de crianças na sala e na escola... Enfim, o professor não deve ter medo de provocar e propor situações desafiadoras; pelo contrário, deve arriscar e oportunizar que o aluno erre e aprenda com seu erro, por meio de uma mediação atenta e respeitosa perante a construção do conhecimento de cada um, uma vez que a resolução de problemas, mesmo que pareçam simples, deve ser o ponto central da atuação docente, pois leva o aluno a investigar e compreender os conteúdos matemáticos, desenvolvendo e aplicando estratégias para resolver esses problemas, fazendo relacionar a Matemática de forma atraente e desafiadora.
Contudo, seja em qualquer contexto, torna-se importante que o educador não dê respostas prontas; pelo contrário, que dê ao aluno a satisfação de resolver um problema de forma autônoma: “o verdadeiro prazer em estudar Matemática é o sentimento de alegria que vem da resolução de um problema – quanto mais difícil o problema, maior a satisfação” (Thomas Butts).
Um caminho para o cálculo
Em busca de compreender o caminho que a criança percorre da saída do eixo da escrita e comparação de números para chegar ao eixo do cálculo/operações, torna-se imprescindível abranger os conhecimentos numéricos de que ela necessita para apoiar esta construção. As crianças que fazem contagens de outras formas normalmente estão mais próximas ao eixo do cálculo. Mas, afinal, qual é a diferença entre a criança que conta e a criança que calcula?
Na tentativa de compreender a diferença entre o aluno que se apoia na contagem e o que se apoia no cálculo, uma das possibilidades adotadas pelo educador é a investigação através do aumento das grandezas numéricas em situações que requerem soluções de “problemas”, pois quando os educandos estão no universo dos números perceptivos acabam permanecendo em uma zona de conforto cognitiva, considerando que esses números são mais facilmente memorizados. Por outro lado, ao possibilitar situações de desequilíbrio mental em que o aluno deve raciocinar frente a números maiores, aos quais não está acostumado, faz-se possível perceber quais alunos apoiam-se na contagem (estratégia de contar de 1 em 1) e quais colocam em ação seus conhecimentos sobre as operações, ou seja, aqueles que conseguem encontrar estratégia para resolver um problema com maior facilidade.
Antes de aprofundarmos as questões voltadas a situações de cálculo mais complexas, torna-se importante compreender as estratégias que as crianças usam na tentativa de fazer representações numéricas. No início do processo de construção de ideias para solução de cálculos, normalmente as crianças necessitam materializar as quantidades, por meio de representações pictográficas em grandes desenhos, e posteriormente em representações de menor escala, como pauzinhos, bolinhas e/ou através da materialização com os próprios dedos. Conforme a criança vai sendo desafiada pelas situações propostas pela educadora, como propriamente o uso de quadros numéricos de base 10, ditados numéricos, comparação de números, compartilhamento de pensamento entre os pares (por meio de grupos de atividades e/ou discussões coletivas sobre as conjecturas elaboradas pelos colegas, frente a uma situação problema), espera-se que, com as constantes experiências e investigações numéricas, ela possa realizar a passagem das representações pictóricas para a chegada das representações numéricas.
Nesse sentido, podemos inferir a existência de dois polos para a solução de situações matemáticas: o das representações figurativas e o das representações matemáticas. Pode-se dizer, em linhas gerais, que o primeiro polo se relaciona com estratégias de resolução apoiadas na contagem, demandando a materialização da quantidade por meio de representações de desenhos e/ou objetos. O segundo polo apoia-se em técnicas fundadas no cálculo, já realizando representações numéricas convencionais (apesar de ainda poder utilizar, em alguns casos, como recursos os próprios dedos para apoiar a solução do cálculo) e os estudantes estão construindo um caminho para o uso de algoritmos convencionais – algoritmos correspondem a técnicas convencionadas na matemática que permitem a obtenção de resultado em determinada operação independentemente dos números a serem utilizados –, denotando conhecimentos mais consolidados e maior compreensão frente ao sistema de numeração decimal.
Em um viés pedagógico, compreende-se que a passagem da contagem para o cálculo demanda sobretudo um ambiente educador que propicie muitas experiências numéricas, harmonizando situações de cálculo que desvelam experiências das crianças e que sejam potencialmente significativas, o que atua como uma base necessária para o desenvolvimento de noções de cálculo. Esses são alguns exemplos de atividades que podem ser inspirações para desenvolver com as crianças e inseri-las de forma envolvente e natural no eixo das operações aritméticas; no entanto, a princípio o trabalho do educador pauta-se na busca pelo avanço do aluno, trabalhando com as representações numéricas, sem aprofundar em questões de sinais numéricos como, + “mais”, – “menos” ou = “igual”, ou seja, é um percurso anterior à chegada de cálculos maiores e a “oficialização” das operações.
Em segundo momento, a atuação do educador deve caminhar para procedimentos que levem as crianças a pensar sobre cálculos de maior complexidade, chegando à compreensão das proposições de adição e subtração. Mas como as crianças aprendem as operações aritméticas? No eixo das operações, intrinsecamente da adição e subtração, é muito comum que as situações que as envolvem sejam inseridas às crianças por meio de situações que as levem a colocar em ação seus conhecimentos frente ao cálculo, utilizando estratégias que facilitem a resolução e apoiem-se em regularidades do sistema de numeração decimal, como reiteram Lerner e Sadovsky (1996, p. 148): “refletir a respeito da vinculação entre as operações aritméticas e o sistema de numeração conduz a formular ‘leis’ cujo conhecimento permitirá elaborar procedimentos mais econômicos”; isso leva a refletir que, para uma situação de adição ou subtração, uma criança, ao não dispor do resultado memorizado, vai partir de seus conhecimentos já consolidados, fazendo uso de estratégias que possam levar a uma melhor solução do cálculo. Por exemplo, na tentativa de resolver (52+14), pode partir da utilização de cálculos mais simples para resolver o cálculo complexo; dentre várias estratégias que poderia adotar, uma possível seria fazer uso da interpretação aditiva de dez como via de acesso para a soma, ou seja, compreende que 52 corresponde a (10+10+10+10+10+2) e 14 se converte em (10+4), podendo somar primeiro as parcelas de dez, totalizando 90, ou fazer uma analogia: assim como 5+4 é 9, 50 + 40 é 90, percebendo regularidades do sistema de numeração, utilizando um cálculo de apoio, e posteriormente somando esse resultado com 2 e 4, obtendo assim a resolução do cálculo.
Outro exemplo viável seria na solução de um cálculo de subtração, (15–9); neste caso a criança poderia reagrupar o número para facilitar a resolução, pensando: “Não sei resolver diretamente 15–9, mas sei que o 9 corresponde a 5 + 4 (decompõe o subtraendo), e o número ao qual quero retirar termina com 5; assim, reagrupando o 9, consigo me ‘livrar’ do 5 e facilitar o restante do meu cálculo, pois ficarei com um número que termina com 0”. Esse pensamento de encontrar estratégias para facilitar o cálculo expressa a compreensão que o aluno possui sobre as regularidades ou “leis” do sistema de numeração decimal. E como o professor pode trabalhar esses conhecimentos com os alunos?
Para trabalhar as questões de cálculo, adição e subtração, não existem fórmulas mágicas ou receitas prontas; o que deve haver é uma real preocupação do professor com a aprendizagem dos alunos, não limitando ou restringindo as numerações, pois desde muito cedo os alunos podem ser apresentados aos números com grandezas maiores, uma vez que no cotidiano deles não existirão essas restrições, os números aparecerão pequenos e grandes ao mesmo tempo, e é preciso dar autonomia ao aluno, permitindo que ele perceba regularidades do sistema e faça generalizações para procedimentos de maior complexidade, não entregando algoritmos prontos de início, propiciando o processo de descoberta da organização do sistema. Assim como a abordagem das características dos números e suas proposições, como a decomposição, a construção de algoritmos convencionais, traduzidos na conta armada, configura-se como produto final nessa construção do pensamento sobre o cálculo, expressando que a ação docente no ensino da Matemática busca a chegada da convencionalidade, porém compreende que esse produto é proveniente de um processo que requer discussões e uma variedade de possibilidades e oportunidades para que as crianças construam suas próprias estratégias e seu próprio caminho para pensar os algoritmos, mas em concomitância o educador deve oportunizar aos alunos a compreensão dos procedimentos, para que eles possam ter autonomia para decidir em qual momento utilizar uma estratégia ou outra.
Trazendo para um viés de ensino da Matemática, o professor ao facilitar a compreensão da conta armada, intrinsecamente de adição e subtração, deve apoiar-se em mais de um procedimento para resolução do cálculo, tendo clareza a curto e a longo prazo das metas de aprendizagem que deseja atingir, uma vez que a compreensão de determinado procedimento de subtração, por exemplo, impactará diretamente na maneira que fará uma das etapas da divisão. O fato é que a linguagem que o educador decide adotar deve propiciar facilidade da inserção dos alunos no raciocínio matemático, que poderá ser aplicado em outras situações. Então, como o educador pode estimular o raciocínio matemático para adição e subtração como conta armada?
A compreensão das regras do sistema de numeração decimal e utilização convencional de algoritmos torna-se uma tarefa complexa do ponto de vista da construção do pensamento, mas por outro lado é uma tarefa muito viável se o aluno estiver em um ambiente que o auxilie nessa construção e propicie o desvelar de habilidades voltadas ao cálculo mental (a ideia de representação mental de situações de cálculo, de forma refletida e pensada, atuando como procedimentos mentais que permitem o aluno ser autor de seus próprios procedimentos e estratégias) e a estratégias de resolução. Para a solução de contas armadas de adição e subtração, torna-se imprescindível a construção de ideias de “desagrupamento” e de ordem decimal, seja por meio de atividades de manipulação de cédulas de dinheiro ou o comumente utilizado material dourado. Vale ressaltar que no processo de descobertas, o educador pode e deve utilizar uma linguagem matemática convencionada, para que os alunos se adaptem a esse raciocínio e possam ler e escrever matematicamente.
Por exemplo, na proposta de resolução do cálculo (460–154), o aluno que apresenta bom estímulo relacionado às questões de desagrupamento e ordem decimal, ao armar a conta poderá apoiar-se em dois procedimentos (dependerá da escolha feita pelo educador para o ensino), um pautado na decomposição e outro na compensação, que são propriedades da subtração, que estão apresentados na Figura 1.
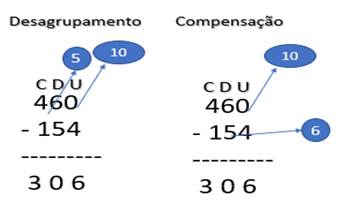
Figura 1: Conta armada - subtração
O procedimento de desagrupamento parte da ideia de que todo número pode ser decomposto, utilizando as características do próprio número. No exemplo de cálculo apresentado, temos a ideia inicial do agrupamento 4 centenas (400), 6 dezenas (60) e 0 unidades, correspondendo ao 460; 1 centena (100), 5 dezenas (50) e 4 unidades (4), correspondendo ao 154. Para solução dessa subtração, espera-se que o educando seja capaz de compreender que, como não consegue retirar diretamente 0 unidades de 4 unidades, precisa desagrupar 1 dezena das 6 que possui o minuendo (460), ficando 5 dezenas. Essa 1 dezena será reagrupada na ordem das unidades; como tinha 0 unidades, ficará com 10 unidades para retirar 4 unidades do subtraendo, resultando em 6 (é importante evidenciar que no desagrupamento o número permanece o mesmo, porém agrupado de forma diferente, enquanto antes se tinha 400+60+0, agora temos 400+50+10). Posteriormente, na ordem das dezenas, o aluno deverá retirar 5 dezenas de 5 dezenas, resultando em 0 dezenas. E, por fim, na ordem das centenas, teremos 4 centenas para retirar 1 centena, resultando em 3 centenas.
No segundo procedimento, a compensação, agora a ideia não é mais de troca/desagrupamento, e sim de variar as grandezas de forma igual. No exemplo, verifica-se novamente que 0 unidades não podem tirar 4 unidades; então é possível “dar” 10 unidades ao 0 e compensar dando 1 dezena ao 50 do subtraendo, ficando com 6 dezenas (164); prosseguindo, teremos que 10 unidades menos 4 unidades resultam em 6 unidades, 6 dezenas menos 6 dezenas correspondem a 0 dezenas e por fim 4 centenas menos 1 centena teremos 3 centenas. Note que no caso da compensação o minuendo e o subtraendo são alterados, porém na mesma proporção; então tinha-se 400+60+0 e passou-se a ter 400+60+10, e ao mesmo tempo no subtraendo tinha-se 100+50+4 e passou-se a ter 100+60+4.
Para desenvolver esses procedimentos, faz-se necessária a possibilidade de colocá-los em prática por meio de exercícios ou situações problema, em um ambiente propício a trocas e à aprendizagem. Mas em que consiste esse ambiente?
Na perspectiva pedagógica, torna-se possível evidenciar a importância de um ambiente de aprendizagem que possa proporcionar trocas de saberes de forma em que todos os envolvidos aprendam e ensinem, com um real envolvimento dialógico. Nesse viés, tem-se as denominadas “investigações matemáticas”, que consistem em práticas de investigação promovidas na sala de aula com foco na Educação Matemática, pautadas na problematização, reflexão e discussões, que podem levar à consolidação dos conhecimentos de forma mais ativa e significativa por parte dos alunos. Ponte; Brocardo e Oliveira (2003, p. 25) apontam que
uma atividade de investigação desenvolve-se habitualmente em três fases (numa aula ou conjunto de aulas): (i) introdução da tarefa, em que o professor faz a proposta à turma, oralmente ou por escrito; (ii) realização da investigação, individualmente, aos pares, em pequenos grupos ou com toda a turma; e (iii) discussão dos resultados, em que os alunos relatam aos colegas o trabalho realizado.
Como apontado pelos autores, a investigação busca propor uma aula mais leve no sentido de não focar somente em transmitir saberes, mas sim pautada em uma construção deles com maior ênfase na atuação do aluno, o qual passa a integrar seus conhecimentos matemáticos em busca de descobrir regularidades da investigação que está realizando com seus pares, aprendendo a ler e a escrever matematicamente, e nesse processo cabe ao professor o papel de mediador, providenciando estimular as descobertas e propor desafios plausíveis ao grupo em questão, de tal forma que sinta-se motivado a continuar as investigações e partilhar suas conjecturas e conclusões com os colegas, questionando e sendo questionado naturalmente. Uma aula pautada nas investigações torna-se um ambiente de descobertas, inquietações, trocas e aprendizados, propício às explorações com números.
Mas, afinal, como propor atividades no ambiente de investigações?
Por muito tempo, educadores acreditavam que havia apenas uma trajetória no aprendizado de Matemática, um único caminho para uma única resposta, como reitera D’Ambrósio (1989, p. 15):
Sabe-se que a típica aula de Matemática, em nível de primeiro, segundo ou terceiro graus, ainda é uma aula expositiva, em que o professor passa para o quadro-negro aquilo que ele julgar importante. Os alunos acreditam que a aprendizagem se dá através de um acúmulo de fórmulas e algoritmos, nada podendo gerar e criar, tornando o papel da disciplina passivo e desinteressante.
Com base no que o autor pontua, o ensino de Matemática não é ensinar a resposta ou como se deve chegar à resposta; é descobrir caminhos possíveis até chegar à conclusão. Propor atividades de investigação para o aprendizado de Matemática é possibilitar que os alunos pensem, descubram e solucionem os problemas se apoiando em conhecimentos prévios ou usando a imaginação de como deve ser resolvido o problema. Com essas atividades sendo propostas de forma correta, dando oportunidade aos alunos por si sós de descobrir soluções diversas, será desenvolvido o raciocínio lógico.
Dessa forma, precisamos pensar em abordagens a partir desse lúdico, pois nessa abordagem há várias vantagens para incentivar a aprendizagem nos anos iniciais e permite utilizarmos materiais que possam auxiliar na construção do conhecimento dos alunos. As vantagens que permeiam esse uso podem ser: a construção do raciocínio lógico, a interação dos alunos, o aprender brincando e a prática de atividades de suas vivências na elaboração de conhecimentos (Alves, 2016, p. 2).
Segundo Alves, para que aspectos como raciocínio lógico, autonomia do pensar e interesse pela Matemática possam ser desenvolvidos de forma produtiva e significativa, faz-se necessário propor aos alunos atividades que façam parte do cotidiano deles, atividades que sejam mais próximas à realidade, pois somente assim eles poderão estabelecer relações com suas imaginações e o conhecimento prévio. Por exemplo, propor atividades lúdicas para que os alunos possam compreender mais ativamente a construção do conceito de números, os valores de cada número, até chegar à construção dos algoritmos convencionais na forma de conta armada. Segundo Almeida (1995 apud Alves, 2016, p. 4),
a educação lúdica contribui e influencia na formação da criança, possibilitando um crescimento sadio, um enriquecimento permanente, integrando-se ao mais alto espírito democrático enquanto investe em uma produção séria do conhecimento. A sua prática exige a participação franca, criativa, livre, crítica, promovendo a interação social e tendo em vista o forte compromisso de transformação e modificação do meio.
Dessa forma, torna-se possível compreender que quando se trabalha com atividades lúdicas facilita-se o processo de aprendizado dos alunos, fugindo do ensino mecânico e partindo para um ensino ativo e significativo. Nas atividades de investigação, os alunos a princípio precisam compreender a proposta da atividade; o orientador não deverá dizer o que eles precisam fazer, mas sim deixá-los livres para pensar e construir hipóteses, tendo o ambiente de aprendizagem favorável a esse processo. Durante as investigações, faz-se necessário que o docente esteja acompanhando cada fala, cada atitude e cada modo de pensar dos alunos, para que possa compreender seus raciocínios e processos, e baseado nisso propor novas atividades para que eles possam estar em contínuo desenvolvimento. Após a investigação, é necessário que o professor possibilite a discussão dos resultados entre todos os alunos para que eles possam expor suas metodologias, como pensaram, o que fizeram e por que fizeram desse jeito, e assim eles irão sintetizar seus pensamentos e refletir sobre eles, em uma perspectiva de aprendizagem mútua e colaborativa.
Considerações finais
O ensino de Matemática não deve ser uma forma de memorização, mas sim uma internalização, na qual os alunos possam compreender as propostas de ensino e se apropriarem delas de forma significativa. Nesse contexto, o ensino da Matemática como forma investigativa traz muitos benefícios aos alunos, pois nesse ambiente eles podem vivenciar mais ativamente seus aprendizados e buscar caminhos diversos para suas respostas, uma vez que na Matemática existem n possibilidades para chegar ao mesmo resultado. Na investigação os alunos desenvolvem o pensamento matemático de forma autônoma, significando e ressignificando mutuamente o seu próprio aprendizado. Com isso, o pedagogo deverá ajudar os alunos na construção de seus pensamentos, atuando como mediador de saberes e não simplesmente como alguém destinado a ensinar regras pouco compreendidas.
Em ambientes de investigação matemática, o próprio professor também estará inserido nos processos de troca que ocorrem na relação mútua entre aprender e ensinar, nos quais é necessário que ele acompanhe cada passo, atitude, forma de pensar, agir e de solucionar os problemas, para, além de nortear sua ação pedagógica, refletir sobre o caminho da aprendizagem dos alunos. Assim, o professor poderá compreender seus alunos e seus anseios, possibilitando preparar atividades mais reflexivas que contribuam em suas necessidades. Contudo, consideramos que o educador, intrinsecamente nos anos iniciais, deverá encorajar os alunos a buscar os próprios caminhos e estratégias para solucionar problemas e juntamente encontrar alternativas de resposta, pois o processo do aprendizado e o entendimento são os elementos mais importantes para os avanços na Matemática.
Referências
ALVES, Luana Leal. A importância da Matemática nos anos iniciais. XXII EREMATSUL – ENCONTRO REGIONAL DE ESTUDANTES DE MATEMÁTICA DO SUL. Centro Universitário Campos de Andrade, Curitiba, 21 a 23 de julho de 2016. Disponível em: https://wp.ufpel.edu.br/geemai/files/2017/11/A-IMPORT%C3%82NCIA-DA-MATEM%C3%81TICA-NOS-ANOS-INICIAS.pdf. Acesso em: 12 jul. 2020.
D’AMBRÓSIO, Beatriz S. Temas e debates. In: ______. Como ensinar Matemática hoje. Brasília: SBEM, 1989. p. 15-19.
KAMII, C. Como as crianças adquirem conceitos numéricos? In: KAMII, C.; HOUSMAN, Leslie Baker. Crianças pequenas reinventam a Aritmética: implicações da teoria de Piaget. Porto Alegre: Artmed, 2002. p. 15-28.
KAMII, C.; HOUSMAN, Leslie Baker. Crianças pequenas reinventam a Aritmética: implicações da teoria de Piaget. Porto Alegre: Artmed, 2002.
LERNER, Delia; SADOVSKY, Patrícia. Os diferentes papéis do professor. In: PARRA, Cecília; SAIZ, Irma (Orgs.). Didática da Matemática: reflexões psicopedagógicas. Porto Alegre: Artes Médicas, 1996. p. 73-154.
PONTE, João Pedro da; BROCARDO, Joana; OLIVEIRA, Hélia Oliveira. Investigações matemáticas na sala de aula. Belo Horizonte: Autêntica, 2003.
Publicado em 01 de dezembro de 2020
Como citar este artigo (ABNT)
SOUZA, Emily Bomfim; KIM, Sônia Cha. Um caminho para o cálculo: O ensino da matemática na perspectiva das investigações. Revista Educação Pública, v. 20, nº 46, 1º de dezembro de 2020. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/20/46/um-caminho-para-o-calculo-o-ensino-da-matematica-na-perspectiva-das-investigacoes
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

