Análise da organização matemática e didática do objeto matemático plano cartesiano presente em um livro didático do 5° ano do Ensino Fundamental
Reginaldo Fabiano da Silva Afonso
Docente universitário (Unipampa - Câmpus Caçapava do Sul), licenciado em Matemática (UFPel), mestre em Matemática (UFRGS), doutorando em Ensino de Ciências e Matemática (UFN)
José Carlos Pinto Leivas
Professor-doutor do Programa de Pós-Graduação em Ensino de Ciências e Matemática (PPGECIMAT/UFN), licenciado em Matemática (UCPel), especialista em Análise Matemática (UFPel), mestre em Matemática e Computação Científica (UFSC), doutor em Educação (UFPR)
O ensino de Geometria é assegurado pela Base Nacional Comum Curricular (Brasil, 2017). Em particular, a abordagem do objeto de conhecimento plano cartesiano é pontuada como um tema a ser tratado na disciplina Matemática ainda nas séries iniciais. De acordo com Thiel (2013), o estudo desse tema visa sustentar que as representações, para fins de comunicação, desempenham papel fundamental, seja no desenvolvimento das representações mentais, na realização de diferentes funções cognitivas ou na produção de conhecimentos.
Segundo os Parâmetros Curriculares Nacionais de Matemática para o Ensino Fundamental (Brasil, 1997, p. 22), é comum os professores elaborarem "as práticas na sala de aula tomando por base os livros didáticos". Na esfera da sala de aula, a prática docente materializa-se por meio da adaptação de saberes que o professor desenvolve com base nos conteúdos presentes nesses materiais. De acordo com Queiróz (2007), "o livro didático vem se constituindo ao longo da história da educação escolar como importante recurso, se não o mais importante recurso, utilizado por professores" (p. 9), pois por meio dele elaboram aulas, saneiam dúvidas sobre assuntos específicos do conteúdo, amadurecem ideias acerca de abordagens de pontos pertinentes e criam atividades relacionadas à sua função de educador.
Considerando a influência que os livros didáticos desempenham no planejamento e no exercício da docência, bem como o interesse no processo de ensino de determinado tema, é importante desenvolver uma pesquisa de natureza praxeológica com vistas ao que e como um dado saber é apresentado nesses tipos de obras. Segundo Chevallard (1999), uma investigação de natureza praxeológica com base na Teoria Antropológica do Didático (TAD) estabelece a atividade matemática e, consequentemente, o estudo da Matemática no conjunto das atividades humanas e das instituições sociais. Essa teoria tem como postulado a ideia de que toda atividade humana pode ser submetida a um modelo denominado praxeologia, que significa um discurso racional da prática. Em nossa investigação, o estudo praxeológico será realizado sobre a abordagem do saber matemático plano cartesiano na obra usada como saber de referência para o ensino; descreveremos os tipos de tarefas e as técnicas de resolução presentes na obra.
O presente trabalho apresentará uma análise das organizações matemáticas e didáticas presentes no livro didático Ápis Matemática, utilizado como referência para o ensino de localização no primeiro quadrante do plano cartesiano através de pares ordenados para as turmas do 5° ano do Ensino Fundamental do Instituto Estadual de Educação Dinarte Ribeiro, situado na cidade de Caçapava do Sul/RS. A finalidade desse estudo é compreender como foram estabelecidas as organizações matemáticas e didáticas presentes no livro citado, adotado pela instituição, em relação ao saber matemático plano cartesiano.
Para alcançar tal objetivo, traçamos os seguintes objetivos específicos:
- Caracterizar as organizações matemáticas e didáticas presentes no livro didático Apis Matemática, utilizado como referência para o ensino de localização no plano cartesiano através de pares ordenados.
- Analisar as organizações matemáticas e didáticas presentes no livro didático Apis Matemática, utilizado como referência para o ensino de localização no plano através de pares ordenados.
- Descrever como foram desenvolvidos, na obra analisada, os seis momentos didáticos descritos por Chevallard (1999).
Para obter os objetivos traçados, adotamos a abordagem qualitativa, a qual foi executada via análise documental do livro didático Apis Matemática correspondente ao 5° ano do Ensino Fundamental. Ambas as escolhas são especificadas na seção Metodologia.
O artigo está estruturado da seguinte maneira: no referencial teórico, tratamos dos conceitos primitivos sujeito, instituição e objeto, definidos por Chevallard (2005), e abordamos tanto as praxeologias como os momentos didáticos propostos por Chevallard (1999). Na sequência, descrevemos a metodologia, seguida da análise e discussão dos resultados. Concluímos apresentando nas considerações finais uma síntese acerca das organizações matemáticas e didáticas constatadas no presente trabalho, acompanhada das referências bibliográficas utilizadas.
Referencial teórico
Atualmente, uma das maiores inquietações na educação é a busca pela mudança no processo de ensino-aprendizagem, almejando um processo compartilhado, sendo ele orientado e coordenado pelo professor, mas com profunda participação individual e de grupos de alunos (Moran, 2000). Nesse contexto, o docente do 5° ano do Ensino Fundamental realiza transformações sobre o saber matemático plano cartesiano presente nos livros didáticos para torná-lo objeto de ensino para os discentes presentes em sua classe, de modo a dar significado a tal objeto.
O fenômeno de transformações sobre o saber pode ser estudado pela denominada Teoria Antropológica do Didático (TAD), desenvolvida por Yves Chevallard (1999). Essa teoria se propõe a analisar um dos problemas do professor, que é preparar suas aulas e colocá-las em prática, ou seja, como selecionar aquilo que constituirá o objeto de estudo (matemático) a ser trabalhado em classe e como fazê-lo funcionar no exercício da docência.
A TAD é composta por três conceitos primitivos: os objetos "O", os sujeitos "X" e as instituições "I". Entretanto, como em qualquer área do conhecimento, outros conceitos serão acrescentados de acordo com a complexidade do estudo.
O objeto O é a primeira noção fundamental introduzida pelo autor. Segundo Chevallard (1998a), "chamamos de objeto qualquer entidade, concreta ou abstrata, que exista para pelo menos um indivíduo. A noção de objeto é aqui a mais geral possível. Tudo é um objeto, inclusive as pessoas" (p. 1, tradução nossa). Nesse contexto, o objeto O é a pedra fundamental da TAD, sendo possível estabelecer um paralelo com a Matemática atual edificada na teoria dos conjuntos, na qual tudo é elemento de um conjunto. Portanto, na TAD, podemos interpretar sujeitos ou instituições também como objetos.
A existência de um objeto está garantida desde que ele seja reconhecido por um sujeito X ou instituição I. A partir de então, iniciará a relação pessoal de X com O, que será denotada por R (X, O) e a relação institucional de I com O, denominada RI (O).
O objeto O existe para o sujeito X se X tem uma relação pessoal com ele, designada de R (X, O): relação de X com O. Igualmente, o objeto O existe para a instituição I – é um objeto institucional para I – se I tem uma relação institucional com O, RI (O). Notemos que esse objeto existe – é um objeto – se é um objeto ao menos para um sujeito X ou uma instituição I. Dado isto, dizemos que X conhece O se X tem uma relação com O (o que significa dizer que O existe para X). Diremos que, para o sujeito Z de uma instituição I, X conhece O se Z supõe um juízo de conformidade de R (X, O) com RI (O) (Chevallard, 2005, p.148-149, tradução nossa).
As noções de instituição I e sujeito X também compõem o escopo teórico da TAD. Segundo Chevallard (1998a), "uma instituição I é um dispositivo social <<total>>, que permite – e impõe – aos seus sujeitos, ou seja, às pessoas X que venham ocupar diferentes posições p oferecidas em I, a utilização de maneiras específicas de fazer as coisas e, de forma mais ampla, o uso de determinadas praxeologias" (p. 1, tradução nossa). Nesse sentido, as instituições I fixam as formas de fazer e de pensar que serão aceitas em seus domínios e os sujeitos X de I exercerem suas funções de acordo com sua posição em I, regidos pelas demandas, hábitos e normas dela. Devemos perceber a instituição I como uma estrutura heterogênea, em que existem várias relações de sujeitos X com objetos O que pertencem a I.
Na citação anterior, a palavra "impõe" remete a deveres do sujeito X para com a instituição I que ele frequenta. Entretanto, a relação entre o sujeito X e a instituição I também traz benefícios ao primeiro. Tal entendimento vem da palavra permite, empregada no sentido de comportar oportunidades para o sujeito X acessar construções humanas presentes na sociedade. Nesse âmbito, os benefícios de frequentar instituições para a inserção social são pontuados por Chevallard:
Uma sociedade é feita de obras, ou seja, de construções humanas que visam trazer respostas a certas questões que são a razão de existência dessas obras. É fácil dar uma lista de obras – moedas, a noção de ângulo, decimais, touradas [...], são obras. Muitas vezes é mais difícil declarar o propósito das obras – por exemplo, ensino de Matemática.
Entrar na sociedade, socializar, é entrar em contato com as obras que a constituem, e em algumas delas para se tornar os atores. [...] A entrada de uma pessoa em uma obra, que participa por definição da socialização da pessoa, contribui ao mesmo tempo para a sua formação, na medida em que essa pessoa se submete à disciplina do trabalho – esportivo, jurídico, artístico, matemático [...] etc.
Qualquer instituição é, portanto, uma operadora de ingresso em determinadas obras e, consequentemente, um agente de socialização e treinamento do seu sujeito (Chevallard, 1998b, p. 1, tradução nossa).
Após já termos refletido sobre os conceitos de objeto, instituição e sujeito, estamos aptos a compreender como Chevallard entende aprendizagem. Para ele, a aprendizagem em uma instituição I ocorre quando a relação entre o sujeito X e o objeto O (R (X, O)) se altera no decorrer do tempo. Caso a relação, na instituição I, entre o sujeito X e o objeto O permaneça estagnada com o passar do tempo, entende-se que não houve aprendizagem. A didática da TAD aflora na intencionalidade da instituição I em proporcionar a transformação na relação R (X, O), de modo a alcançar uma equivalência entre as relações R (X, O) e RI (O) (sujeito – objeto e instituição de objeto) ou, ainda, a relação entre sujeito e objeto (R (X, O)) contempla as expectativas pretendidas pela instituição I para com aqueles que tomassem conhecimento de tal objeto institucional (RI (O)).
Existindo um processo de alteração na relação R (X, O) de modo que seja desejável chegar a RI (O), é introduzida a avaliação institucional. Segundo Chevallard (2005), essa avaliação é um dos mecanismos segundo os quais I é levada a pronunciar, por meio de alguns dos seus agentes, uma sentença de conformidade (ou de não conformidade) entre R (X, O) e RI (O).
Após descrevermos como se estabelecem as relações entre objeto, sujeito e instituição, iremos apresentar a noção de praxeologia citada na definição de instituição, identificando elementos que influenciam no planejamento das aulas por parte do professor e como ele as executa no cenário didático.
Chevallard (1999) acredita que a praxeologia adotada em uma instituição é definida por uma quádrupla ordenada [T, t, θ, Θ], onde: T é o tipo de tarefa a ser executada; a maneira de realizá-la e aceita pela instituição, a qual é identificada pelo autor como técnica, denotada por t; o suporte tecnológico-teórico (ou saber) compõe a tecnologia θ utilizada em I e, por fim, a teoria Θ deverá justificar e embasar a tecnologia θ empregada nos domínios de I.
Além do entendimento dos quatro entes que compõem a praxeologia, é pertinente ter a noção de que cada tipo de tarefa (T) pode apresentar subtipos de tarefas (ti), e isso é o cerne de uma praxeologia, visto que permite direcionar o grau de dificuldade segundo o qual um objeto de estudo pode ser tratado em determinado nível de ensino. Mais que isso: dependendo da complexidade da tarefa (T) a ser executada, várias técnicas podem ser acionadas, pois uma técnica (t) pode não ser suficiente para dar conta de todos os subtipos de tarefas ti relacionadas à tarefa T.
A iteração entre as coordenadas da praxeologia [T, t, θ, Θ] implica um movimento de um conjunto prático-técnico (concebendo o saber-fazer) e um conjunto tecnológico-teórico (sustentado pelo saber).
Além do modelo praxeológico apresentado para análise do saber matemático, Chevallard (1999) afirma que, para compreendermos o estudo de determinado tema matemático, é necessário analisar sua organização matemática e a organização didática. Sobre a organização matemática, o autor sugere que ela permite justificar, entender e resolver situações apresentadas, sendo composta pelos tipos de tarefas matemáticas (T) executadas pelas técnicas matemáticas utilizadas, tecnologias embasadas e de teorias que também são de origem matemática.
Por outro lado, a maneira, como é desenvolvido o estudo de uma organização matemática, denominada organização didática, é compreendida por Chevallard (1999) assim:
por organização didática podemos entender, a priori, o conjunto dos tipos de tarefas, de técnicas, de tecnologias etc., mobilizadas para o estudo concreto em uma instituição concreta. O enfoque clássico em didática da Matemática tem ignorado em geral os aspectos mais genéricos de uma organização de estudo de um tipo dado de sistemas didáticos (Chevallard, 1999, p. 239).
A organização didática, diferentemente de uma organização matemática, é de natureza didática e surge da necessidade de definir como deve ser realizado o estudo de determinado tema no interior de uma instituição, com o objeto de estudo e as metodologias adequadas à instituição e às pessoas que participam dela. Com esse objetivo, o autor define seis momentos didáticos: primeiro encontro com a praxeologia matemática estudada; exploração do tipo de tarefa e elaboração de técnicas; constituição do ambiente tecnológico e teórico; trabalho da técnica; institucionalização; e, por último, a avaliação.
Em nosso trabalho, os três conceitos primitivos – O, I, X – serão, respectivamente: plano cartesiano, Instituto Estadual de Educação Dinarte Ribeiro (IEEDR), docentes no IEEDR que adotaram o referido livro. Já a quádrupla ordenada [T, t, θ, Θ] é, respectivamente: localização no plano cartesiano, par ordenado, sistemas coordenados, Geometria Analítica.
Metodologia
Para alcançar os objetivos traçados, adotamos a abordagem qualitativa. Segundo Bogdan e Biklen (1982), essa metodologia envolve a aquisição de dados descritivos provenientes do contato do pesquisador com o objeto de estudo, destacando mais o processo do que o produto. Nesse sentido, mapeamos as organizações matemáticas e didáticas presentes no livro adotado pela instituição em relação ao saber matemático plano cartesiano, pertinente ao 5° ano do Ensino Fundamental.
O meio utilizado para chegar aos objetivos propostos foi a análise documental do livro didático citado. Gil (2008) pontua que a análise documental busca identificar informações que permitam interpretá-las de acordo com os objetivos da pesquisa. Por esse viés, discorremos sobre as organizações matemáticas e didáticas presentes no livro didático. As organizações matemáticas foram avaliadas quanto aos tipos de tarefas trabalhadas na obra e as justificativas das técnicas empregadas no desenvolvimento das seções referentes ao tema. Já as organizações didáticas foram classificadas quanto às escolhas didáticas efetuadas pelo autor no emprego dos momentos didáticos para estruturar a obra. O livro foi aprovado no PNLD de 2019 e tem como referência bibliográfica a seguinte descrição:
DANTE, Luiz Roberto. Ápis matemática: 5° ano: Ensino Fundamental, anos iniciais. 3ª ed. São Paulo: Ática, 2017.
A investigação consistiu em identificar, modelar e analisar as praxeologias presentes na obra referenciada, sem deixar de explorar as organizações matemáticas e didáticas presentes nela.
Resultados e discussão
O livro didático analisado tem a Unidade 2 destinada ao estudo de Geometria; mais especificamente, retas paralelas e retas concorrentes são abordadas em uma subseção de tal capítulo. Em particular, essa partição aborda dois temas relacionados a sistemas de coordenadas: Localização no plano usando pares ordenados e Deslocamento no plano.
O primeiro tema – Localização no plano usando pares ordenados – é introduzido com o enunciado da relação biunívoca existentes entre pontos do primeiro quadrante e pares ordenados. A Figura 1 mostra aquilo que caracteriza o primeiro encontro com a praxeologia matemática a ser estudada.

Figura 1: Apresentação da praxeologia matemática referente a pares ordenados
Fonte: Dante (2017, p. 53).
Entendemos que a Figura 1 caracteriza o primeiro momento didático descrito por Chevallard, visto que o autor da obra analisada propõe o encontro entre o objeto de estudo e o leitor, apresentando a funcionalidade da adoção de sistemas de coordenadas.
Na sequência, Dante passa à institucionalização do conceito de par ordenado no primeiro quadrante, o que é apresentado na Figura 2.

Figura 2: Institucionalização de pares ordenados
Fonte: Dante (2017, p. 53).
Apresentamos a Figura 2 como materialização da institucionalização do conceito de par ordenado, pois mostra a organização matemática em jogo no cenário didático, apontando os elementos que permanecerão definitivamente e aqueles que serão dispensados.
A exploração do tipo de tarefa e a elaboração de técnicas são trabalhadas simultaneamente, bem como a constituição do ambiente tecnológico e teórico, conforme exposto na Figura 3. Em nosso caso, isso é representado pelo diálogo entre os dois personagens do livro-texto, que fomenta as discussões que levam à resolução de um problema e à execução da tarefa. Por sua vez, a constituição do ambiente tecnológico e teórico relativo às técnicas empregadas está implícita. Entretanto, mostra-se de acordo com a complexidade esperada para o 5° ano do Ensino Fundamental.
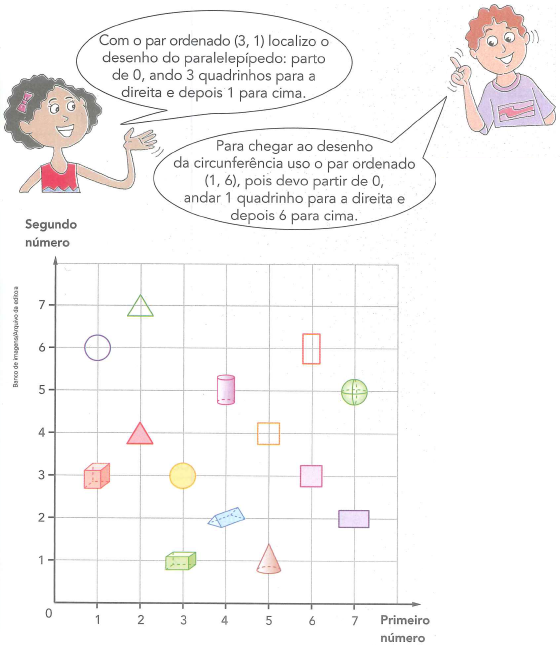
Figura 3: Exemplos que exploram as tarefas, técnicas e situam o ambiente tecnológico-teórico
Fonte: Adaptado de Dante (2017, p. 53).
Ainda na Figura 3, podemos constatar as técnicas utilizadas para abordagem de dois tipos de tarefa (T1 e T2), enunciadas da seguinte maneira:
T1: Localizar e identificar uma figura, dado o par ordenado.
T2: Determinar o par ordenado correspondente à figura dada.
O livro-texto apresenta, por meio da resolução de exemplos presentes no diálogo dos personagens, as técnicas (t1 e t2) a serem implementadas para solucionar, respectivamente, as tarefas T1 e T2. Elas podem ser generalizadas da seguinte maneira:
t1: identificar as componentes do par ordenado; partindo da origem, efetuar os deslocamentos horizontal e vertical correspondentes às entradas; e, por fim, classificar a figura presente na posição correspondente ao par ordenado fornecido inicialmente.
t2: localizar a figura no plano cartesiano; observar o deslocamento para a direita e para cima, partindo da origem e visando chegar a tal figura; e, por fim, determinar o par ordenado com os dados correspondentes à posição da figura fornecida inicialmente.
Quanto ao trabalho da técnica, as tarefas T1 e T2 são exploradas na seguinte proporção: 7 tarefas do tipo T1 e 5 tarefas do tipo T2, conforme ilustrado na Figura 4. Tais atividades possibilitam colocar em prática as técnicas estudadas, vivenciando-as e explorando seu alcance na resolução de problemas.
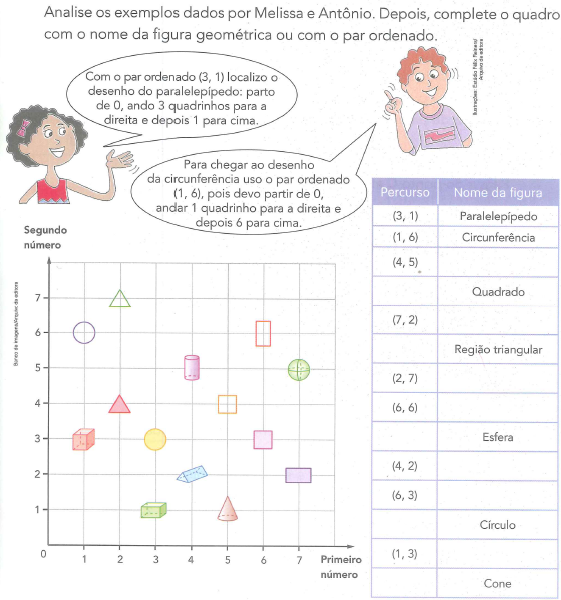
Figura 4: Exercícios que abordam as tarefas T1 e T2, bem como as técnicas correspondentes
Fonte: Dante (2017, p. 53).
À medida que avançou a abordagem do tema, a complexidade das atividades propostas também foi incrementada. Em uma segunda subseção do livro foram explorados deslocamentos no plano, onde foram trabalhados novos tipos de tarefas e técnicas para a resolução. A primeira delas é ilustrada na Figura 5, de modo que definimos a tarefa e a técnica correspondentes da seguinte maneira:
T3: localizar, identificar e descrever o deslocamento entre dois pontos no plano cartesiano, dada uma dupla de pares ordenados correspondentes a cada um desses pontos.
t3: identificar as componentes de cada par ordenado; localizar os pontos correspondentes aos pares ordenados no plano cartesiano; efetuar o deslocamento horizontal ou vertical – exclusivamente – de modo a partir do ponto inicial e chegar ao ponto final; completar as lacunas indicadas no exercício.
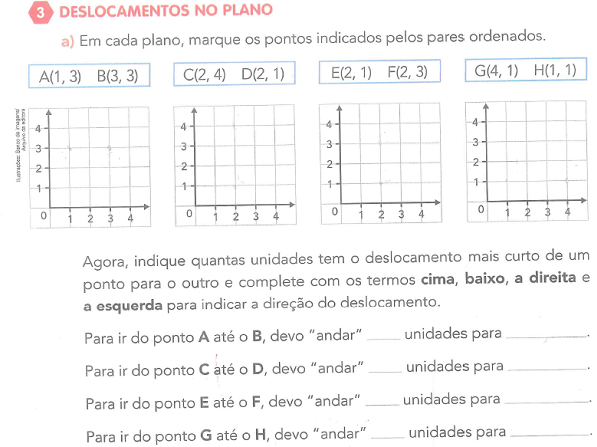
Figura 5: Exercícios que abordam a tarefa T3 e a técnica correspondente
Fonte: Dante (2017, p. 54).
Observamos que na Figura 5 são propostas quatro tarefas do tipo T3 que apresentam interdependência com as anteriores do tipo T1, visto que a tarefa T3 pede a localização de um ponto dado o par ordenado correspondente. T3 vai além de T1 ao explorar nas ultimas quatro linhas o sentido empregado no deslocamento horizontal (à direita ou à esquerda), bem como o sentido implementado no deslocamento vertical (para cima ou para baixo).
Ainda explorando o deslocamento no plano, o autor apresenta o exercício ilustrado na Figura 6, o qual interpretamos como composto pela tarefa T4 e que pode ser tratado pela técnica t4 descritas a seguir:
T4: determinar dois pares ordenados correspondentes a dois pontos, bem como a localização do ponto final no plano cartesiano, dada a localização do ponto inicial e o deslocamento vertical necessário para ir do ponto inicial ao final.
t4: localizar o ponto inicial no plano cartesiano e identificar as componentes que formam seu par ordenado; completar as lacunas referentes às coordenadas do ponto de partida; efetuar o deslocamento vertical descrito no enunciado de modo a partir do ponto inicial e chegar ao ponto final; localizar o ponto final no plano cartesiano e identificar as componentes que formam seu par ordenado; completar as lacunas referentes às coordenadas do ponto de chegada.
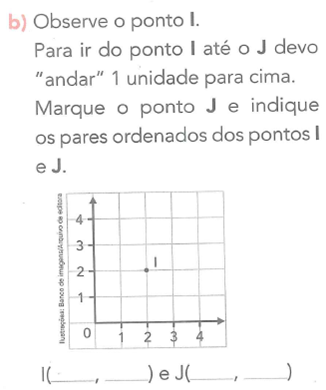
Figura 6: Exercício que aborda a tarefa T4 e a técnica correspondente
Fonte: Dante (2017, p. 54)
Observamos que na Figura 6 é proposta uma única tarefa do tipo T4, a qual apresenta interdependência com dois exercícios do tipo T3, explorando, de certo modo, o caminho inverso, em que é dado o ponto inicial, a direção e o sentido do deslocamento para ir até o ponto final e pede, também, o ponto de chegada. Acreditamos que mais tarefas desse tipo seriam pertinentes para fixação da técnica, e o autor poderia ter explorado não só o deslocamento vertical como também o deslocamento horizontal, visando dar fundamentação para a última tarefa proposta, mas não menos complexa que as atividades precedentes.
No último exercício proposto referente ao assunto tratado, extraímos a tarefa T5 e a técnica t5, as quais podem ser conferidas na Figura 7. A seguir, explicitamos T5 e t5.
T5: determinar a localização, no plano cartesiano, do ponto de partida e do de chegada, bem como o par ordenado do ponto de chegada, dado o par ordenado correspondente ao ponto inicial e os deslocamentos horizontal e vertical necessários para ir do ponto inicial ao final.
t5: identificar as componentes que formam o par ordenado correspondente ao ponto de partida e localizá-lo no plano cartesiano; efetuar os deslocamentos verticais e horizontais descritos no enunciado partindo do ponto inicial para atingir o ponto final; localizar o ponto final no plano cartesiano e identificar as componentes que formam seu par ordenado; completar as lacunas referentes às coordenadas do ponto de chegada.
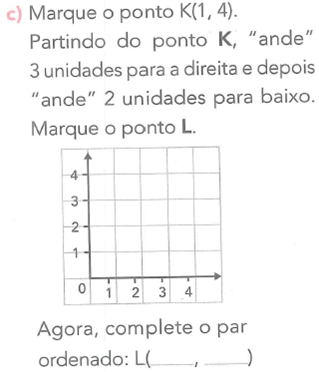
Figura 7: Exercício que aborda a tarefa T5 e a técnica correspondente
Fonte: Dante (2017, p. 54).
Em síntese, as organizações matemáticas analisadas no livro texto incidiram sobre a identificação dos tipos de tarefas presentes na obra para o estudo do saber matemático em questão e das técnicas mobilizadas para o desenvolvimento dos referidos tipos de tarefas encontrados. Além disso, buscamos compreender o entorno tecnológico-teórico mobilizado para justificar o uso das técnicas apresentadas. Assim como as organizações matemáticas, as organizações didáticas também foram bem exploradas no decorrer do assunto analisado no livro, tendo em vista que foram desenvolvidas por meio de uma amarração com os temas sólidos geométricos, regiões planas e polígonos, os quais precediam o tema pares ordenados.
Considerações finais
A análise realizada sobre a obra adotada como saber de referência para o ensino de 5° ano do Instituto Estadual de Educação Dinarte Ribeiro mostrou que o saber matemático 1° quadrante do plano cartesiano foi explorado. Sua abordagem deu-se por duas vertentes principais: localização e deslocamento no primeiro quadrante do sistema cartesiano. Além disso, foi apresentada a existência da relação biunívoca entre pontos do primeiro quadrante e pares ordenados, o que possibilitou a atribuição de significado à Matemática trabalhada.
As organizações matemáticas referentes à localização no plano, usando pares ordenados, continham um número expressivo de exercícios. Isso, tanto na seção que abordava o tema localização no primeiro quadrante quanto nos exercícios propostos referentes a esse assunto, possibilitou detectar duas tarefas cujas técnicas de resolução foram construídas durante seu desenvolvimento e usadas para o enfrentamento das atividades apresentadas.
Na abordagem do tema "deslocamento no plano", o número de tarefas identificadas aumentou em três unidades e o número de exercícios apresentados diminuiu progressivamente, chegando à proporção de uma tarefa para um exercício nas duas últimas atividades propostas. Acreditamos que nessa parte do livro-texto o autor poderia ter proposto mais exercícios, visando dar maior notabilidade ao momento conhecido como trabalho da técnica, em que o discente tem a oportunidade de exercer a autonomia na resolução de exercícios e fixar aquilo que foi trabalhado em classe. Além disso, com um maior número de atividades similares à da Figura 6 e ao explorar o deslocamento horizontal, poderia ser construído um caminho natural para a resolução da atividade da Figura 7, em que ocorrem os deslocamentos horizontal e vertical em uma mesma questão.
Em linhas gerais, podemos dizer que todos os momentos didáticos foram desenvolvidos na obra analisada – alguns com mais afinco, como o primeiro encontro com a praxeologia estudada sendo explorado o tipo de tarefa e elaborada uma técnica e o respectivo trabalho dessa técnica. Por sua vez, o momento avaliação não se mostrou claro para todas as atividades no livro-texto avaliado. Acreditamos que tal momento poderia ficar mais explicito ao final do capítulo, abordando exercícios sobre localização e deslocamento no plano cartesiano, ou seja, na seção "Vamos ver de novo?", em que são propostos exercícios de revisão.
A organização didática foi contemplada pela conexão entre assuntos da própria Matemática, caracterizando, assim, um certo tipo de abordagem didática que quebra o tratamento linear e hierárquico dado ao estudo dos saberes matemáticos, o que é recomendado pelos Parâmetros Curriculares Nacionais. A técnica empregada para enfrentar as tarefas do tipo T1 e T2 (vide Figura 4), por exemplo, envolveu estudos relacionados não só com localização no plano cartesiano como também sólidos geométricos, regiões planas e polígonos, o que ratifica o trabalho de vinculação entre os saberes.
Como desdobramento do presente trabalho, pretendemos estender a análise das organizações matemáticas e didáticas pertinentes ao tema plano cartesiano para outros livros adotados na rede pública de ensino de Caçapava do Sul referentes ao 5° ano do Ensino Fundamental. Tal mapeamento de tarefas e técnicas presentes nesses livros didáticos poderá trazer contribuições para escolhas didáticas assertivas de seus leitores. Para além disso, uma ampliação deste estudo pode ir para livros didáticos do Ensino Médio e Superior, uma vez que as três etapas poderão oferecer aos pesquisadores da teoria de Chevallard uma amplitude prática encontrada na literatura que o professor desses níveis pode usufruir para sua atuação profissional embasada em uma teoria consolidada.
Referências
BRASIL. Base Nacional Comum Curricular (BNCC). Educação é a Base. Brasília, MEC/Consed/Undime, 2017. Disponível em: http://basenacionalcomum.mec.gov.br/download-da-bncc. Acesso em: 11 set. 2018.
______. MEC. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais. Brasília: MEC/SEF, 1997.
BOGDAN, R.; BIKLEN, S. K. Qualitative research for education. Boston: Allyn and Bacon, 1982.
CHEVALLARD, Y. Organisations Didactiques: 1. Les cadres généraux. 1998a. Disponível em: http://yves.chevallard.free.fr/spip/spip/IMG/pdf/Organisations_didactiques_1_1998_.pdf. Acesso em: 20 fev. 2021.
______. Questions vives, savoirs moribonds: le problème curriculaire aujourd"hui. 1998b. Disponível em: http://yves.chevallard.free.fr/spip/spip/IMG/pdf/YC_1997_-_Defendre_transformer.pdf. Acesso em: 20 fev. 2021.
______. El análisis de las prácticas docentes en la teoría antropológica de lo didáctico. Recherches en Didactique des Mathématiques, v. 19, nº 2, p. 221-266, 1999.
______. La transposición didáctica. 3ª ed. Buenos Aires: Aique, 2005.
DANTE, L. R. Ápis matemática: 5° ano: Ensino Fundamental, anos iniciais. 3ª ed. São Paulo: Ática, 2017.
GIL, A. C. Como elaborar projetos de pesquisa. São Paulo: Atlas, 2008.
MORAN, J. M. Mudar as formas de ensinar e aprender com tecnologias. 2000. Disponível em: http://www.eca.usp.br/prof/moran/site/textos/tecnologias_eduacacao/uber.pdf. Acesso em: 20 fev. 2021.
QUEIROZ, E. O uso do livro didático de Matemática por professores de Ensino Fundamental. Dissertação (Mestrado em Educação) - Universidade Federal de Pernambuco, Recife, 2007.
THIEL, A. A. Práticas matemáticas no plano cartesiano: um estudo da coordenação de registros de representação. 2013. 235f. Tese (Doutorado em Educação Científica e Tecnológica) - Centro de Ciências Físicas e Matemáticas, Universidade Federal de Santa Catarina, Florianópolis, 2013.
Publicado em 13 de abril de 2021
Como citar este artigo (ABNT)
AFONSO, Reginaldo Fabiano da Silva; LEIVAS, José Carlos Pinto. Análise da organização matemática e didática do objeto matemático plano cartesiano presente em um livro didático do 5° ano do Ensino Fundamental. Revista Educação Pública, v. 21, nº 13, 13 de abril de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/12/analise-da-organizacao-matematica-e-didatica-do-objeto-matematico-plano-cartesiano-presente-em-um-livro-didatico-do-5-ano-do-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

