O ensino de Matemática durante a pandemia: proposta de atividade sobre semelhança de triângulos com uso do software GeoGebra Geometria
Álida Rinara Souza Morais
Licenciada em Matemática (IFMG – Câmpus Formiga)
Lorraine Borges Silva
Licenciada em Matemática (IFMG – Câmpus Formiga)
Dandara Lorrayne Nascimento
Doutoranda e mestra em Modelagem Matemática e Computacional (Cefet). professora no IFMG
Este trabalho apresenta um relato de experiência desenvolvido com uma turma do 9º ano da rede pública de ensino da cidade de Japaraíba/MG, durante a pandemia causada pelo novo coronavírus. Trata-se de uma proposta de atividade envolvendo o conteúdo de semelhança de triângulos e o uso do aplicativo GeoGebra Geometria, cujo intuito era compreender a formulação das conjecturas iniciais dos alunos sobre o conceito de semelhança de triângulos frente aos resultados coletados.
O surgimento e a propagação do novo coronavírus SARS-CoV-2 em território chinês no final de 2019 provocou a maior política de distanciamento social já vista (Arruda, 2020). O isolamento social promoveu transformações severas, comércios tiveram que seguir normas de funcionamento específicas e o acesso presencial às escolas foi bloqueado (Senhoras, 2020).
O ineditismo desse acontecimento gerou receio em inúmeros grupos sociais, dentre eles os profissionais da Educação, que tiveram de se adaptar e se reinventar para o novo método de ensino, o ensino remoto, criado para que os estudantes tenham a possibilidade de dar continuidade ao processo de desenvolvimento cognitivo e retomar a realização de algumas atividades educacionais, mesmo que distantes do convívio escolar (Arruda, 2020; Minas Gerais, 2020a).
Diante desse cenário, a utilização de recursos tecnológicos se apresenta como uma eficiente ferramenta nos processos de ensino-aprendizagem, pois permite a difusão do conhecimento e compartilhamento de informações, promovendo o contato de alunos e professores, de forma que o processo educacional continue (Silva; Neto; Santos, 2020). Mesmo diante das diversas ferramentas tecnológicas disponíveis para o uso educacional, é importante que o professor busque metodologias que favoreçam a aprendizagem dos seus alunos e faça um planejamento adequado. Nessa busca, “os softwares de Matemática dinâmica surgem como uma possibilidade que pode oferecer aos alunos ambientes de aprendizagem mais interessantes, onde eles podem testar e experimentar” (Braz; Souza; Silva, 2019, p. 4).
Dentre os softwares existentes, o GeoGebra Geometria é uma alternativa interessante para os professores de Matemática, em especial para o ensino de Geometria, devido à possibilidade de construções e visualizações em duas ou três dimensões, como apresentado na Figura 1.
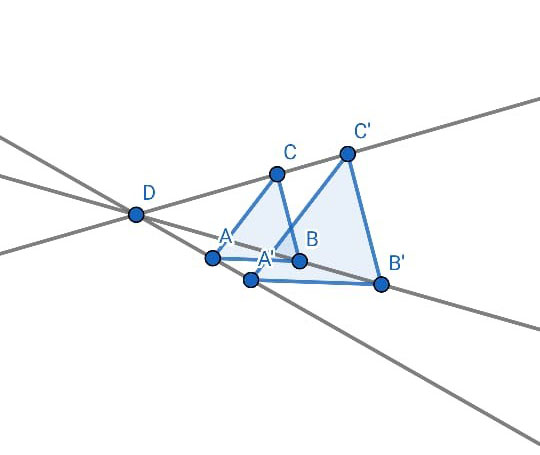
Figura 1: Triângulos semelhantes
Além dessas características, o GeoGebra é um software gratuito que pode ser utilizado de forma online ou offline, podendo ser baixado diretamente em computadores e/ou dispositivos móveis. O uso desse recurso facilita a compreensão pela visualização e permite que os alunos levantem conjecturas, explorem, manipulem as construções, propiciando momentos de argumentação e validação (Oliveira; Guimarães; Andrade, 2012). Nascimento et al. (2017) acrescentam que associar o ensino de Geometria aos softwares educacionais e às atividades de natureza exploratório-investigativa é uma forma mais efetiva de proporcionar a compreensão dos conceitos estudados e despertar o interesse dos alunos pelas aulas, sobretudo pelo conteúdo de semelhança de triângulos, que, segundo Cabral e Almeida (2020), tem sido prejudicado quando abordado por métodos de mecanização e abstração que, ao invés de dar ênfase ao processo de construção do conhecimento do aluno, valorizam apenas o resultado e a memorização de fórmulas.
Dessa forma, o objetivo deste trabalho é apresentar um relato de experiência vivenciado em tempos de pandemia com uma proposta de atividade, envolvendo o conteúdo de semelhança de triângulos e o uso do aplicativo GeoGebra Geometria, possibilitando que os alunos criassem uma conjectura inicial a respeito do tema e fossem sujeitos ativos e autônomos na construção do próprio conhecimento.
Para atingir esse objetivo, a atividade foi desenvolvida com uma turma de 22 estudantes do 9º ano do Ensino Fundamental da Escola Estadual Padre Pedro Lamberti, na cidade de Japaraíba, em Minas Gerais. A escolha da turma ocorreu devido ao fato de uma das autoras ser a professora da turma, facilitando assim o contato com os alunos.
Procedimentos metodológicos e a pesquisa
Para desenvolver o trabalho, foi utilizada a pesquisa qualitativa, pois esta consiste em uma relação dinâmica entre o mundo real e o sujeito, tendendo a analisar os dados indutivamente e preocupando-se mais com o processo e o significado do resultado do que o produto (Prodanov; Freitas, 2013). Assim, o objetivo da pesquisa é analisar as respostas dos alunos frente aos resultados coletados, a fim de compreender a formulação de suas conjecturas iniciais sobre o conceito de semelhança de triângulos.
Além do objetivo inicial relatado, a proposta também teve o intuito de complementar e enriquecer os materiais disponibilizados pela Secretaria de Estado de Educação de Minas Gerais. Após auxiliar os estudantes no download do aplicativo, a construção da atividade de semelhança de triângulos (Figura 2) foi realizada no aplicativo para celular GeoGebraGeometria, pois, de acordo com o Cetic (2020), é o mais utilizado.

Figura 2: Sequência de construção da atividade
Para que os alunos explorassem a construção realizada e criassem suas primeiras conjecturas a respeito do conteúdo de semelhançade triângulos, foi enviado um questionário, via Google Forms (Figura 3) juntamente com o passo a passo da construção.

Figura 3: Questionário da atividade
Para auxiliar os alunos na construção no aplicativo GeoGebra Geometria, com o intuito de obter maior participação, as pesquisadoras criaram seis grupos no WhatsApp, com cerca de quatro alunos em cada, pois, de acordo com Prado e Almeida (2003, p. 72 apud Borba; Malheiros; Amaral, 2007, p. 36), a função principal do educador é “orientar a aprendizagem dos alunos – uma aprendizagem que se desenvolve na interação colaborativa [...], propiciando a criação de uma rede de comunicação e colaboração, na qual todos se inter-relacionam”.
Assim, foi organizado um horário de estudo de aproximadamente duas horas para cada grupo, em que as docentes realizaram a construção junto a eles, intervindo com comentários em momentos pertinentes, com o intuito de “propor questões que conduzam o aluno a produzir significado relacionados ao conteúdo a ser abordado” (Pironel; Vallilo, 2017, p. 294).
Para finalizar a pesquisa, foi enviado um questionário final (Figura 4), via Google Forms, a fim de conhecer a opinião dos alunos acerca da utilização da tecnologia como metodologia para o ensino da Matemática em tempos de pandemia.

Figura 4: Questionário final
O ensino remoto
Devido à pandemia causada pelo novo coronavírus (covid-19), o distanciamento social foi apontado como a principal medida de prevenção ao vírus, fazendo com que os estabelecimentos comerciais seguissem normas específicas de funcionamento e as escolas fossem fechadas (Minas Gerais, 2020b). Essas ações causaram diversas mudanças no dia a dia das pessoas, inclusive na vida dos alunos. Diante dessa nova realidade, os profissionais da Educação tiveram que se reinventar, buscando estratégias para seguir com suas atividades educacionais (Senhoras, 2020).
Nesse momento, a utilização de recursos tecnológicos pode se apresentar como uma ótima ferramenta para o ensino remoto, cuja aplicação deve ser realizada com planejamento e considerando as desigualdades sociais locais, pois muitos alunos não possuem condições favoráveis de estudo, existindo vários fatores externos que podem criar limitações e gerar desmotivação no aprendizado, como os aspectos sociais, econômicos e emocionais (Dias, 2021).
A pesquisa TIC Domicílios de 2019, realizada pelo Comitê Gestor da Internet no Brasil (CGI), por meio do Centro Regional de Estudos para o Desenvolvimento da Sociedade da Informação, aponta que 71% dos domicílios possuem acesso à internet e que o dispositivo mais utilizado para esse fim é o celular, sendo usado por 99% de usuários por rede (Cetic, 2020). Diante disso, os responsáveis pela educação devem refletir sobre a implementação de práticas pedagógicas que atendam a essas necessidades, considerando a melhor forma de adaptar os conteúdos a essa ferramenta.
Apesar das diversas ferramentas disponíveis para o ensino a distância, nem todas são eficazes no processo de ensino-aprendizagem. Portanto, o professor deve analisar qual dos recursos melhor irá se adequar como método de ensino para atender seus alunos, sempre levando em consideração a realidade deles.
A implementação do ensino remoto permitiu aos alunos o acesso à educação por ambientes virtuais em diferentes localidades, porém o professor ainda mantém papel fundamental para o processo de ensino-aprendizagem. Nesse contexto, Silva e Silva (2016) citam que a importância do educador e a sua responsabilidade social seriam potencializadas:
não mais seria passar conteúdos dos quais “só ele possuiria”, mas orientar o processo de construção do conhecimento pelo aluno, apontando-lhe a necessidade de uma atitude crítica e ativa em relação ao mundo de informações a que é submetido diariamente. Caberia ao professor fazer o aluno compreender que, com as informações recebidas, ele pode construir conhecimento e fazer ciência e/ou arte, mostrando-lhe alguns possíveis caminhos para isso, possibilitando a recombinação e ressignificação contínua de saberes, fantasias, desejos e lembranças, numa prática pedagógica que viabilizaria a concretização daquilo que a comunidade necessita e deseja (Silva; Silva, 2016, p. 8).
A cada dia que se passa, os professores são mais desafiados, e esse fato evidencia a importância de que os docentes estejam sempre em busca de metodologias que favoreçam a aprendizagem e se mantenham atualizados e capacitados sobre as novas tendências de ensino, especialmente o uso da tecnologia em sala de aula, uma vez que ela está se tornando indispensável para a vida humana (Borba; Penteado, 2016).
O uso das tecnologias digitais no ensino de Matemática
A tecnologia está cada vez mais presente no meio cultural, modificando o comportamento intelectual e afetivo dos jovens, ocasionando a eles “outras maneiras de compreender, de perceber, de sentir e de aprender” (Babin; Kouloumdjian, 1989 apud Porto, 2006, p. 3).
Na educação, os alunos almejam por aulas mais dinâmicas, divertidas, interativas e voltadas para a realidade deles, e este fato não pode ser ignorado pela instituição de ensino, pois “ela só será capaz de alcançar seus objetivos educacionais, através de uma inserção na realidade dos jovens, realidade essa que está fortemente voltada para a utilização dos meios tecnológicos e virtuais” (Nascimento; Ferreira, 2015, p. 4).
De acordo com Pereira (2016), a utilização da tecnologia na Educação pode tornar a aprendizagem mais interativa, modificando as relações entre professor e aluno, uma vez que constitui no educando uma forma significativa de pensar, desenvolvendo sua autonomia e proporcionando a construção de seu próprio conhecimento. Borba e Penteado (2016) acreditam que a utilização das tecnologias possa ser a grande solução para a falta de interesse e a desmotivação dos alunos.
Nessa perspectiva, Pereira (2016) cita:
O ensino de Matemática por meio de atividades que utilizam as ferramentas tecnológicas e pedagógicas atuais contribui efetivamente para tornar o ambiente de aprendizagem mais agradável, melhorando a capacidade de ler e interpretar itens necessários para a construção do conhecimento matemático do aluno, promovendo a autonomia no processo de ensino-aprendizagem (Pereira, 2016, p. 57).
Além disso, a tecnologia possibilita a construção do conhecimento, tanto pelos alunos como pelos professores, de forma ativa, crítica e criativa, servindo para enriquecer o ambiente educacional (Brasil, 1998). A tecnologia também proporciona situações de aprendizagem com maior qualidade, pois cria “ambientes de aprendizagem em que problematização, atividade reflexiva, atitude crítica, capacidade decisória e autonomia sejam privilegiadas” (Brasil, 1998, p. 140-141).
Existem vários softwares e aplicativos educativos que permitem o desenvolvimento das habilidades mencionadas, além de contribuir para o desenvolvimento da estrutura lógica de pensamento do aluno e influenciar de forma significativa no processo de ensino-aprendizagem, inclusive na área de Matemática, podendo ofertar desafios e experiências enriquecedoras.
Vale destacar que, apesar de o uso de um software trazer grandes benefícios, ele não é a salvação para os problemas educacionais, devendo ser visto apenas como uma ferramenta para facilitar e tornar mais dinâmicos os processos de ensino-aprendizagem (Borba; Penteado, 2016). Assim, é preciso que haja discussão e reflexão entre os responsáveis pelo processo educacional para que esses recursos sejam utilizados de modo consciente, eficaz e crítico (Nascimento, 2007).
Diante disso, o GeoGebra Geometria pode se apresentar como uma ferramenta interessante e reveladora para vencer a apatia e a desmotivação dos estudantes, possibilitando uma representação concreta, em que o aprendiz é capaz de enxergar o objeto, representando-o de forma geométrica e algébrica, além de proporcionar que o estudante pense no que está sendo feito e como está sendo feito (Vaz, 2012). “Esse dinamismo possibilita que o aluno perceba diversas relações entre os objetos matemáticos, faça conjecturas e até mesmo formalize os resultados, de forma visual, no próprio software” (Vaz, 2012, p. 40).
Além disso, o GeoGebra é de domínio público, pode ser utilizado sem estar conectado à internet, depois de instalado no celular ou computador; por possuir interface de fácil manipulação, possibilita que os professores e alunos explorem, conjecturem e investiguem novas estratégias de ensino e aprendizagem.
Dessa forma, a presente proposta optou pela utilização do GeoGebra Geometria como abordagem didática para facilitar o ensino de Geometria, em especial o conteúdo semelhança de triângulos, neste período de isolamento social e atividades educacionais remotas.
O ensino de Geometria no Brasil
Com o surgimento da reforma de ensino da “Matemática Moderna”, na década de 1960, o currículo do ensino da Matemática foi modificado, comprometendo a aprendizagem pelo seu método formalista e o esquecimento da disciplina de Geometria (Sousa, 1999). Essa reforma provocou grandes dificuldades, fazendo com que a maioria dos professores abandonassem o ensino de Geometria e dessem maior importância ao ensino de Aritmética e de Teoria dos Conjuntos, ocasionando assim uma crise que se estende até os dias atuais em relação ao ensino-aprendizagem de Geometria (Pavanello, 1993 apud Nascimento et al., 2017).
Apesar das reformas ocorridas, o ensino de Geometria não foi o mesmo, pois, de acordo com Avila (2010), no cumprimento de todos os conteúdos programáticos de Matemática e pela insegurança dos professores, a Geometria é deixada para o final do ano letivo, fazendo com que ela não seja ensinada devidamente.
Embora haja um grande impasse no ensino de Geometria, ela é fundamental na formação dos alunos, pois “sem conhecer Geometria a leitura interpretativa do mundo torna-se incompleta, a comunicação das ideias fica reduzida e a visão da Matemática torna-se distorcida” (Lorenzato, 1995, p. 5).
Lorenzato (1995) ressalta que a Geometria está em toda parte, que através dela se desenvolve o pensamento geométrico, o raciocínio visual e ela facilita a compreensão e a resolução de inquisições relacionadas a outras áreas do conhecimento. Assim, para que se desenvolvam esses aspectos, é importante que o ensino da Geometria “não se limite apenas à automação, memorização e técnicas operatórias baseadas em processos de abstração”, o que ainda, segundo esse autor, ocorre com o ensino de semelhança de triângulos (Cabral; Almeida, 2020, p. 2).
Em relação ao ensino de semelhança de triângulos, a Base Nacional Comum Curricular relata que, nessa etapa, devem ser abordadas as “tarefas que analisam e produzem transformações e ampliações/reduções de figuras planas, identificando seus elementos variantes e invariantes” (Brasil, 2017, p. 273).
Dessa forma, com o intuito de encorajar o ensino de Geometria e torná-la algo mais fácil e divertido de se aprender, é importante que o professor busque novas metodologias, a fim de despertar o interesse do aluno, possibilitando que ele seja o construtor de seu próprio conhecimento (Lorenzato, 1995).
Análise dos resultados
Os resultados foram obtidos pelas observações realizadas pelas pesquisadoras, pelos registros feitos pelos alunos no questionário que acompanha a construção e pela análise do questionário final de avaliação da atividade.
É importante ressaltar que, como uma das autoras era a professora da turma, ela tinha conhecimento de que os alunos haviam tido aulas com o uso de tecnologias como o software GeoGebraGeometria e que eles perteciam a uma classe social média baixa, em que nem todos tinham acesso aos recursos tecnológicos: quatro alunos trabalhavam para ajudar a família financeiramente e dois moravam na zona rural.
Mesmo com a criação dos grupos no WhatsApp, aproximadamente 45% dos estudantes participaram. Vale destacar que as professoras se colocavam à disposição para esclarecer possíveis dúvidas dos alunos e enviavam mensagens individuais para promover a participação e entender o motivo da ausência deles, ação que vai ao encontro dos pensamentos de Borba, Malheiros e Amaral (2007, p. 44) ao afirmarem que cabe “aos professores responsáveis identificar aqueles que não se manifestam ao longo da discussão e questioná-los”, mas na maioria dessas tentativas, as docentes eram ignoradas.
Compreensão dos alunos acerca do conteúdo de semelhança de triângulos
Durante a construção, os alunos apresentaram dúvidas em relação ao motivo da utilização da homotetia para gerar a ampliação ou redução do triângulo desenhado. As autoras então, corroborando a ideia de Passos (2009) ao anunciar que é importante a adoção de materiais manipuláveis como suporte na aprendizagem, pois proporcionam melhor compreensão e interpretação do que está sendo ensinado, utilizaram o exemplo da lanterna do celular, que, projetando uma figura na frente do aparelho, emitirá uma sombra na parede; assim, o celular funciona como um ponto fixo que amplia ou reduz a figura, mantendo as características principais dela, como a forma e os ângulos. Foi observado o seguinte diálogo no grupo 1:
Professora: Pensem na lanterna do celular de vocês como se fosse o ponto D, coloquem um objeto na frente da lanterna e percebam que a sombra desse objeto será projetada na parede (nesse momento a professora enviou uma foto com o teste que ela tinha feito com um post-it, para que os alunos pudessem visualizar melhor). Percebam que o formato do post-it, que é um quadrado, está ampliado na parede. Essa é a ideia de homotetia, e é o que está acontecendo com o triângulo.
Aluna A: Ah! Estamos construindo a sombra de um triângulo.
Professora: Não seria a sombra do triângulo, mas a ampliação ou redução dele. Apresentei a ideia da sombra para vocês poderem compreender. Esse valor de 1,5 que colocamos na construção significa o fator de ampliação ou redução do triângulo de vocês, ou seja, a quantidade que ele aumentou ou reduziu. Tudo bem até aqui? Podemos continuar?
Grupo: Sim!
Aluno B: Eu fiz o teste com uma caixinha pequena. A sombra ficou maior mas ficou com o mesmo formato.
Como as aulas ministradas eram síncronas, as pesquisadoras aguardavam que os alunos enviassem o print de cada passo das construções para prosseguir à próxima etapa, evitando assim possíveis equívocos na construção. A Figura 5 apresenta o print da construção realizada pela aluna A.
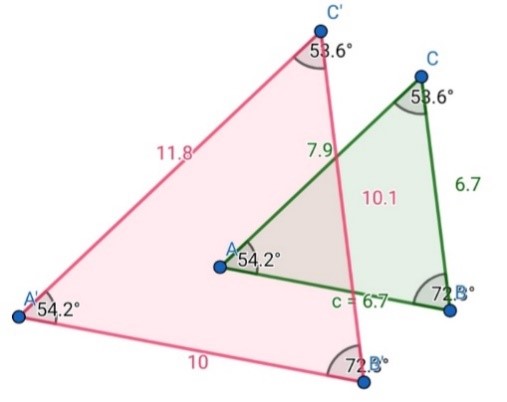
Figura 5: Construção da aluna A
Em relação à análise do questionário da atividade (Figura 3), na segunda pergunta, que indagava sobre o que os alunos podiam observar em relação ao cálculo das razões entre os lados e o que esses resultados significavam, percebe-se que os alunos compreenderam o motivo de as razões serem iguais; apesar de nem todos responderem que os segmentos são proporcionais, eles conseguiram perceber que esse fato ocorre pela realização da homotetia, como mostra a Figura 6. Preocupa o fato de que o motivo de alguns alunos não apresentarem a proporção dos segmentos como justificativa da questão talvez se deva por não lembrarem do conceito de proporcionalidade.

Figura 6: Resposta dada pela Aluna C frente à pergunta 2 do questionário da atividade
Ao serem questionados sobre o que acontece quando os resultados das divisões dos segmentos resultam em 1, os alunos tiveram dificuldade em interpretar o enunciado da questão; as autoras tiveram que voltar ao exemplo da lanterna do celular para que compreendessem melhor, conforme mostra o diálogo a seguir.
Professora: Então vamos voltar ao exemplo da lanterna. Suponha que o fator de aumento utilizado na projeção do post-it fosse de 1,5 vezes maior, ok? Mas e se agora o fator for 1 vez maior ou 1 vez menor, o que aconteceria?
Aluna D: Não faria diferença.
Aluna E: Ele vai continuar do mesmo tamanho, eu acho.
Percebe-se que depois dessa explicação os alunos conseguiram compreender melhor o enunciado da questão, formulando respostas coerentes, como apresenta a Figura 7.

Figura 7: Resposta da Aluna F dada à questão 3 do questionário da atividade
Após solicitar que os alunos movimentassem os vértices dos triângulos e observassem o que aconteceria, todos perceberam que, conforme aumentavam ou diminuíam o tamanho do triângulo, as medidas dos ângulos continuavam as mesmas, mas alguns apresentaram a homotetia como justificativa de esse fato ocorrer, conforme mostra a Figura 8. Apenas um aluno citou que isso decorre devido ao fato de as medidas dos lados serem proporcionais.

Figura 8: Resposta dada pelo Aluno B frente à questão 4 do questionário da atividade
Muitas vezes, os alunos usavam a homotetia como justificativa para as perguntas, não observando o real significado da definição de semelhança de triângulos. Preocupa o fato de eles associarem sempre semelhança de triângulos ao conceito de homotetia, quando um não depende do outro para existir. Mas isso foi esclarecido em uma reunião que as pesquisadoras realizaram via Google Meet, em que elas deixaram claro qual era a diferença entre esses conceitos.
Na questão 5, ao serem questionados sobre as características comuns aos dois triângulos construídos, quase todos os alunos justificaram que as características comuns aos dois triângulos são os ângulos e as formas, não citando que os lados são proporcionais. Talvez esse fato tenha se dado pelo motivo de a questão anterior tratar de ângulos, em que os alunos consideraram apenas os fatos verificados nela, esquecendo as constatações realizadas em momentos anteriores ou, como citado, por não lembrarem o conceito de proporcionalidade.
Ao solicitar que os alunos definissem com suas palavras o que são dois triângulos semelhantes, apenas um aluno conseguiu se aproximar da definição correta do conceito de triângulos semelhantes, como apresenta a Figura 9.

Figura 9: Resposta do Aluno B à questão 6 do questionário da atividade
Muitos alunos confundiram triângulos semelhantes com triângulos iguais (Figura 10); outros apresentaram apenas uma semelhança entre eles, como ângulos iguais ou lados proporcionais.

Figura 10: Resposta da Aluna A frente à questão 6 do questionário da atividade
Percebe-se que a maioria dos alunos tinha uma noção intuitiva do conceito, mas não conseguia expressá-lo de forma precisa. Vale salientar que o objetivo da atividade foi apenas fazer com que os alunos criassem uma concepção inicial que se aproximasse da definição de semelhança de triângulos. Dessa forma, para evitar que os alunos criassem falsas conjecturas a respeito do conteúdo, ao final da atividade foi realizada uma reunião pelo Google Meet a fim de que os estudantes sanassem suas dúvidas e refletissem sobre suas respostas referentes ao questionário da atividade, pois essa fase é fundamental “para que os alunos possam desenvolver a capacidade de comunicar e de refletir sobre o seu trabalho e o seu poder de argumentação” (Ponte; Brocardo; Oliveira, 2016, p. 41). Posteriormente, a professora regente formalizou o conceito de semelhança de triângulos.
Percepção dos discentes em relação à atividade proposta na condição de ensino remoto
Dentre os 22 alunos matriculados e frequentes durantes as aulas presenciais, apenas 10 participaram da atividade, o que corresponde a aproximadamente 45% do total. Pesquisas apontam que essa baixa participação está acontecendo em escolas públicas do país inteiro. Fraga (2020) destaca que “a falta de equipamentos eletrônicos e a falta de acesso à internet são os principais motivos para a ausência de retorno dos alunos sobre as tarefas e incentivo e apoio das famílias ao ensino remoto” (Fraga, 2020, s/p).
Dentre os alunos, 1,8% trabalhava para poder auxiliar financeiramente em casa. O ensino remoto acaba por possibilitar essa geração de renda, fazendo com que o aluno opte pelo mercado de trabalho em um horário em que deveria estar presente nas aulas remotas, o que também pode ser motivo para a baixa participação (Dias, 2021). As pesquisadoras se deparavam, frequentemente, com a demora em obter respostas dos alunos durante a construção, o que se acredita que tenha ocorrido, assim como afirma Sacco (2012), pelas distrações a que o aluno está sujeito no ambiente domiciliar, não podendo ser controlado durante a atividade a distância. Além disso, durante a construção no aplicativo do GeoGebraGeometria, muitos alunos precisaram interromper a execução da atividade por causa de compromissos marcados, como dentista, médico ou por depender do acesso aos aparelhos dos pais, que, como ressalta Fraga (2020), muitas vezes estão fora de casa.
Assim, percebe-se que os fatores associados às condições sociais e habitacionais podem estar agregados ao acesso e participação dos alunos durante o ensino remoto, além de aspectos emocionais; o atual cenário pode afetar na adaptação, motivação e nos engajamentos dos alunos aos estudos (Dias, 2021).
Apesar das dificuldades apresentadas, a análise do questionário de avaliação da atividade realizada pelos alunos evidencia que um dos objetivos do trabalho foi alcançado, pois o uso de recursos tecnológicos como método de ensino permitiu a compreensão do conteúdo de semelhança de triângulos, tornando a aprendizagem mais fácil, conforme cita a aluna F (Figura 11).

Figura 11: Resposta da aluna F frente à questão 2 do questionário de avaliação
Além disso, na fala “É mais fácil entender a matéria na prática”, do Aluno B, percebe-se que o aplicativo GeoGebraGeometria permitir a visualização do objeto em diferentes ângulos possibilita ao aluno “pensar de uma forma matematicamente diferente do que se estivéssemos trabalhando como uma construção estática ou apenas falando dela, sem nenhum recurso visual” (Rodrigues; Santos, 2014).
Percebe-se então que essas respostas expressam as ideias de Borba e Penteado (2016), Pereira (2016) e Porto (2006) mencionadas no referencial teórico do trabalho, ao citarem que o uso da tecnologia no ensino contribui para um ambiente de aprendizagem mais agradável, facilitando a aprendizagem e permitindo ao aluno outras formas de compreender.
Assim, ressalta-se a importância de os professores adotarem estratégias de ensino diferenciadas, pois elas fazem com que os alunos sintam maior gosto por explorar e adquirir conhecimento. As Figuras 12 e 13 abordam claramente esse conceito; ali os alunos expressam que o uso da tecnologia permite um ensino de Matemática que se opõe a exercícios rotineiros de aplicação e memorização.

Figura 12: Resposta do Aluno B à questão 3 do questionário da avaliação

Figura 13: Resposta da Aluna A à questão 3 do questionário da avaliação
Com base nos resultados abordados, conclui-se que o ensino do conteúdo semelhança de triângulos envolvendo o software GeoGebraGeometria permite uma atividade diferenciada da habitual sala de aula e quadro, proporcionando uma aula mais divertida e prazerosa; além de permitir que o aluno crie uma conjectura inicial sobre semelhança de triângulos, ofertou aprendizagem sobre a utilização de noções geométricas importantes para a construção de polígonos como reta, ponto e ângulo.
Conclusão
No que se refere ao objetivo do trabalho – possibilitar que os alunos criassem uma conjectura inicial a respeito do conteúdo de semelhança de triângulos e fossem sujeitos ativos e autônomos na construção do próprio conhecimento –, foi perceptível que os alunos criaram conjecturas pelas discussões levantadas no momento da construção no software GeoGebraGeometria, porém foram apresentadas deficiências quanto à definição das características comuns dos triângulos e ao uso da homotetia.
A análise dos resultados obtidos evidencia que a utilização do software GeoGebra Geometria possibilitou que os alunos explorassem a sua construção, indo ao encontro das concepções dos autores mencionados quando afirmaram que o uso desse recurso facilita a compreensão pela visualização e permite a manipulação das construções, propiciando momentos de argumentação e validação, experiência que não seria possível apenas com a utilização de lápis e papel.
Pode-se constatar que existem diversos aspectos que estão associados à adesão dos alunos durante o ensino remoto, influenciando diretamente o processo de ensino-aprendizagem, como a falta do contato direto entre professor e aluno, a indisponibilidade dos alunos em participar das aulas online, já que muitos trabalham para ajudar financeiramente em casa e nem todos têm acesso a recursos tecnológicos. Outro aspecto se deve ao fato de o ensino remoto exigir que os estudantes sejam sujeitos autônomos na busca pelo conhecimento, pois durante o processo muitos buscam ou necessitam do auxílio dos pais, que muitas vezes não possuem conhecimento adequado, acesso ao material online ou até mesmo tempo disponível para se dedicar aos estudos com os filhos.
Diante do atual cenário, em que fatores sociais, econômicos e emocionais dificultam a eficácia do ensino remoto, julgamos pertinente, assim como afirmam Silva, Neto e Santos (2020), que os professores analisem suas práticas educativas, levando em consideração a desigualdade social e os demais obstáculos enfrentados por pais e alunos durante a realização das atividades escolares.
Como forma de reaplicação da atividade, as autoras sugerem que a ferramenta homotetia não seja utilizada na construção do triângulo, por poder afetar a compreensão dos alunos quanto à formulação do conteúdo ou, caso desejem usá-la, devem deixar explícito o motivo da sua utilização antes de iniciar a construção. Vale destacar também que essa proposta de atividade pode ser reformulada de modo a abranger todo o conteúdo de semelhança de triângulos, podendo ser aplicada até mesmo fora do contexto do ensino remoto, em aulas presenciais.
Referências
ARRUDA, E. P. Educação remota emergencial: elementos para políticas públicas na educação brasileira em tempos de covid-19. Em Rede – Revista de Educação a Distância, v. 7, nº 1, p. 257-275, 2020.
AVILA, G. Reflexões sobre o ensino de Geometria. Revista do Professor de Matemática, 2010. Disponível em: http://www.rpm.org.br/cdrpm/71/1.html. Acesso em: 5 abr. 2021.
BORBA, M. C.; MALHEIROS, A. S.; AMARAL, R. B. Educação a distância online. 3ª ed. Belo Horizonte: Autêntica, 2007.
BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. 5ª ed. Belo Horizonte: Autêntica, 2016.
BRASIL. MEC. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais - terceiro e quarto ciclos: introdução aos Parâmetros Curriculares Nacionais. Brasília: MEC/ SEF, 1998.
______. MEC. Secretaria de Educação Fundamental. Base Nacional Comum Curricular: Matemática. Brasília: MEC/SEF, 2017.
BRAZ, L. H. C.; SOUSA, J. C. S.; SILVA, L. B. GeoGebra 3D: reflexões a partir de uma proposta para o ensino de prismas e pirâmides. ENCONTRO DE ENSINO E PESQUISA EM EDUCAÇÃO MATEMÁTICA DE OURO PRETO, 10. Anais...Ouro Preto, 2019.
CABRAL, C. A. F.; ALMEIDA, T. C. S. Semelhança de triângulo e GeoGebra: uma alternativa de ensino por meio de representações dinâmicas. Revista Sergipana de Matemática e Educação Matemática, v. 5, nº 1, p. 358-375, 2020.
CENTRO REGIONAL DE ESTUDOS PARA O DESENVOLVIMENTO DA SOCIEDADE DA INFORMAÇÃO (CETIC). Três em cada quatro brasileiros já utilizam a Internet, aponta pesquisa TIC Domicílios 2019. 2020. Disponível em: https://cetic.br/pt/noticia/tres-em-cada-quatro-brasileiros-ja-utilizam-a-internet-aponta-pesquisa-tic-domicilios-2019/. Acesso em: 05 abr. 2021.
DIAS, F. F. Uma experiência com o ensino-aprendizagem de Estatística durante a pandemia: percepções e desafios. Dissertação (Mestrado Profissional em Matemática em Rede Nacional), Universidade Federal de Goiás, Catalão, 2021.
FRAGA, L. Ensino remoto emergencial na rede pública traz muitos desafios. Correio Braziliense, 2020. Disponível em: https://www.correiobraziliense.com.br/app/noticia/eu-estudante/ensino_educacaobasica/2020/07/02/interna-educacaobasica-2019,868923/ensino-remoto-emergencial-na-rede-publica-traz-muitos-desafios.shtml. Acesso em: 05 abr. 2021.
LORENZATO, S. Por que não ensinar Geometria? A Educação Matemática em Revista, v. 3, nº 4, p. 3-13, 1995.
MINAS GERAIS. Decreto nº 47.886, de 15 de março de 2020. 2020b. Disponível em: https://www.portaldoservidor.mg.gov.br/images/caderno1_2020-03-15.pdf. Acesso em: 05 abr. 2021.
NASCIMENTO, D. L.; SÁ, D. L.; VIEIRA, T. P.; BRAZ, L. H. C. Minicurso: construções de triângulos através do software GeoGebra. ForScience, v, 5, nº 3, 2017.
NASCIMENTO, J. K. F. Informática aplicada à educação. Brasília: Ed. Universidade de Brasília, 2007.
NASCIMENTO, J. L. G.; FERREIRA, J. C. A utilização da rede social Facebook como auxílio ao docente em sala de aula. CONGRESSO NACIONAL DE EDUCAÇÃO, 2. Anais... Campina Grande, 2015.
OLIVEIRA, I. L. L.; GUIMARÃES, S. U.; ANDRADE, J. A. A. As potencialidades do GeoGebra em processos de investigação matemática: uma análise do desenvolvimento de objetos de aprendizagem da EaD no ensino presencial. Instituto São Paulo GeoGebra, v. 1, nº 1, 2012.
PASSOS, C. L. B. Materiais manipuláveis como recursos didáticos na formação de professores de Matemática. In: LOREZATO, S. (Orgs.). O laboratório de ensino de Matemática na formação de professores. 3ª ed. Campinas: Autores Associados, 2009. p. 77-92.
PIRONEL, M.; VALLILO, S. A. M. O papel da avaliação na metodologia de ensino-aprendizagem – avaliação de Matemática através da resolução de problemas. In: ONUCHIC, L. R.; LEAL JUNIOR, L. C.; PIRONEL, M. (Orgs.). Perspectivas para resolução de problemas. São Paulo: Editora Livraria da Física, 2017.
PEREIRA, M. F. F. Atividades com o GeoGebra: uma proposta para o ensino de semelhança. JORNADA DE ESTUDOS EM MATEMÁTICA, 2. Anais... Marabá, 2016.
PONTE, J. P.; BROCARDO, J.; OLIVEIRA, H. Investigações matemáticas na sala de aula. 3ª ed. Belo Horizonte: Autêntica, 2016.
PORTO, T. M. E. As tecnologias de comunicação e informação na escola; relações possíveis... relações construídas. Revista Brasileira de Educação, v. 11, nº 31, 2006.
PRODANOV, C. C.; FREITAS, E. C. Metodologia do trabalho científico: métodos e técnicas de pesquisa e do trabalho acadêmico. 2ª ed. Novo Hamburgo: Feevale, 2013.
RODRIGUES, G. D.; SANTOS, L. M. A.O uso do software GeoGebra na resolução de problemas no ensino da Matemática. Monografia (Especialização em Mídias na Educação), Universidade Federal de Santa Maria, Santa Maria, 2014.
SACCO, S. G. Um estudo sobre hábitos e estratégias de aprendizagem na realização da lição de casa de alunos do Ensino Fundamental. Dissertação (Mestrado em Educação), Universidade Estadual de Campinas, Campinas, 2012.
SENHORAS, E. M. Coronavírus e educação: análise dos impactos assimétricos. Boletim de Conjuntura (Boca), v. 2, nº 5, 2020.
SILVA, E. H. B.; NETO, J. G.; SANTOS, M. C. Pedagogia da pandemia: reflexões sobre a educação em tempos de isolamento social. Revista Latino-Americana de Estudos Científicos, v. 1, nº 4, p. 29-44, 2020.
SILVA, W. T.; SILVA, E. N. O papel do docente na educação a distância: perspectivas para o novo profissional. E3 - Revista de Economia, Empresas e Empreendedores na CPLP, v. 2, nº 1, p. 62-75, 2016.
SOUSA, M. C. A percepção de professores atuantes no ensino de Matemática nas escolas estaduais da Delegacia de Ensino de Itu, do movimento Matemática Moderna e sua influência no currículo atual. Dissertação (Mestrado em Educação), Universidade Estadual de Campinas, Campinas, 1999.
VAZ, D. A. F. Experimentando, conjecturando, formalizando e generalizando: articulando investigação matemática com o GeoGebra. Revista Educativa, v. 15, nº 1, p. 39-51, 2012.
Publicado em 13 de julho de 2021
Como citar este artigo (ABNT)
MORAIS, Álida Rinara Souza; SILVA, Lorraine Borges; NASCIMENTO, Dandara Lorrayne. Revista Educação Pública, v. 21, nº 26, 13 de julho de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/26/o-ensino-de-matematica-durante-a-pandemia-proposta-de-atividade-sobre-semelhanca-de-triangulos-com-uso-do-isoftwarei-geogebra-geometria
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

