Práticas de ensino na formação do futuro professor de Matemática
Cristiane de Mello
Licenciada em Matemática (UFSM), mestre em Matemática (UFF), doutora em Ciências (UFRJ), professora adjunta do Departamento de Matemática (UNIRIO)
Loisi Carla Monteiro Pereira
Licenciada, bacharel e mestre em Matemática (UFF), doutoranda em Ciência da Computação com Ênfase em Análise Numérica (UFRJ), professora adjunta do Departamento de Matemática (UNIRIO)
Marcelo Leonardo dos Santos Rainha
Bacharel em Matemática (UFF), mestre em Matemática (UFF), doutor em Engenharia Nuclear (UFRJ), professor adjunto do Departamento de Matemática (UNIRIO)
Durante o ano de 2015, o professor Marcelo Rainha, da Universidade Federal do Estado do Rio de Janeiro (UNIRIO), coordenou um projeto de extensão intitulado Olimpíadas de Matemática: uma nova esperança. O objetivo principal era colaborar com a formação continuada de professores, utilizando a metodologia de Resolução de Problemas, que seria aplicada em conjuntos sociais diversos, induzindo o aluno ao conhecimento através da competitividade e da força do exercício intelectual. Desenvolvido na UNIRIO com a colaboração das professoras Cristiane de Mello, Loisi Carla Pereira e Luzia Martarelli, o projeto contou com a participação de alguns estudantes do curso de licenciatura em Matemática da UNIRIO nas modalidades presencial e a distância (Consórcio Cederj), e de professores das redes municipal e estadual de ensino do Estado do Rio de Janeiro. No decorrer das atividades, além das dificuldades apresentadas pelos estudantes, também observamos muitas deficiências na formação dos professores presentes. Uma delas foi o fato de eles não conseguirem fazer a conexão entre o que eles estudaram na graduação e o que ensinam em sala de aula. Partindo dessa constatação, fomos motivados a preparar um minicurso com o intuito de explorar o conhecimento matemático já construído e desafiar o raciocínio por meio da aplicação de jogos e de outras atividades lúdicas.
Essa preocupação com a ruptura entre a formação inicial dos professores e a escola não é recente. Um fato já observado pelo matemático alemão Felix Klein, em sua obra, hoje clássica, Matemática Elementar de um Ponto de Vista Superior (2009, 2010, 2011),é uma dupla descontinuidadena formação inicial do professor de Matemática: poucas conexões são estabelecidas, por um lado, entre a Matemática dos cursos universitários de formação de professores e aquela anteriormente estudada na escola básica; por outro lado, entre a Matemática dos cursos universitários de formação de professores e aquela que será futuramente praticada em sala de aula.
Assim, não é de se espantar que boa parte dos professores da Educação Básica não consiga fazer a conexão entre o que foi estudado na graduação e o conteúdo que é ensinado em sala de aula. Para um aprendizado de qualidade, é importante que o aluno esteja motivado, sinta-se desafiado e tenha admiração pelo seu professor. Contudo, o professor do ensino básico não tem sido visto ultimamente por seus alunos como uma fonte de conhecimentos interessantes e motivadores. Isso se deve em parte pela forma com que o conhecimento é transmitido. Nossa proposta pretende fortalecer a comunicação professor-aluno, motivando os alunos e capacitando os professores para a elaboração de uma aula mais dinâmica e diversificada. Embasando esta argumentação, Lev Vygotsky (2001, p. 73) estabelece que:
As reações emocionais exercem a influência mais substancial sobre todas as formas do nosso comportamento e os momentos do processo educativo. Queremos atingir uma melhor memorização por parte dos alunos ou um trabalho melhor sucedido do pensamento, seja como for devemos nos preocupar com que tanto uma como outra atividade seja estimulada emocionalmente. A experiência e os estudos mostraram que o fato emocionalmente colorido é lembrado com mais intensidade e solidez do que um fato indiferente. Sempre que comunicamos alguma coisa a algum aluno devemos procurar atingir o seu sentimento. Isso se faz necessário não só como meio para melhorar a memorização e apreensão, mas também como objetivo em si.
Em contrapartida, foi promulgado, em junho de 2014, o Plano Nacional de Educação (PNE), com validade de 10 anos, que prevê como uma de suas estratégias atingir suas metas 12 e 15:
12.7) Assegurar, no mínimo, 10% (dez por cento) do total de créditos curriculares exigidos para a graduação em programas e projetos de extensão universitária, orientando sua ação, prioritariamente, para áreas de grande pertinência social;
15.8) Valorizar as práticas de ensino e os estágios nos cursos de formação de nível médio e superior dos profissionais da educação, visando ao trabalho sistemático de articulação entre a formação acadêmica e as demandas da educação básica;
15.3) Ampliar programa permanente de iniciação à docência a estudantes matriculados em cursos de licenciatura, a fim de aprimorar a formação de profissionais para atuar no magistério da educação básica (Brasil, 2014).
As diretrizes evidenciam, portanto, a necessidade da presença da prática como componente curricular na matriz dos cursos de licenciatura desde o seu início, permeando toda a formação do estudante, futuro professor, inclusive no âmbito das disciplinas específicas do curso em questão e não somente nas disciplinas didático-pedagógicas e de estágio curricular, como ocorre em geral. Desse modo, a universidade não deve ser apenas um polo de produção e disseminação do conhecimento, que muitas vezes se restringe à divulgação em periódicos científicos e conferências acadêmicas, não atingindo alunos e professores da Educação Básica.
O minicurso que será relatado neste trabalho segue exatamente neste sentido: foi preparado e proposto para estudantes de cursos de Licenciatura em Matemática. Seu objetivo principal é proporcionar ao estudante, futuro professor, a oportunidade de conhecer e experimentar algumas práticas de ensino de Matemática para que isso o ajude a construir sua identidade profissional docente. Ao final deste trabalho, poderemos verificar que tal objetivo foi alcançado com sucesso.
Metodologia e resultados alcançados
Nosso minicurso contou com um público de 50 estudantes do curso de licenciatura em Matemática na Universidade Federal de Juiz de Fora (UFJF) e com um público de 35 estudantes do curso de licenciatura em Matemática na Universidade Federal Rural do Rio de Janeiro (UFRRJ) – Unidade Nova Iguaçu. Em ambas as universidades, o número de estudantes inscritos no minicurso correspondeu ao número máximo de vagas oferecidas.
Para cada atividade proposta no minicurso, os estudantes receberam um cartão com as respectivas orientações, que também estavam expostas na tela de projeção da sala de aula, e o material concreto para a execução. As ideias para a criação e elaboração dessas atividades, bem como para a confecção do material concreto surgiram por meio da consulta realizada no site Jogos & Matemática e da leitura, análise e reflexão dos textos de Castro Monteiro e Gaspar (2007), Giraldo (2016), Stewart (2009; 2010) e Fomin, Genkin e Itenberg (2010).
No total, foram realizadas onze atividades envolvendo conteúdos matemáticos do Ensino Fundamental e Médio. Devido ao espaço aqui disponível, apresentamos na sequência a descrição, a aplicação e os resultados alcançados de apenas algumas delas, não menosprezando, de modo algum, as restantes. Consideramos todas de igual importância para o ensino-aprendizagem dos conceitos matemáticos envolvidos.
Atividade 1: Jogo dos sinais
Regras (Jogos/Jogos & Matemática):
- Número de jogadores: 2.
- O jogo contempla todos os números naturais de 1 a 20, e cada jogador começa o jogo com 5 sinais de mais (+) e 5 sinais de menos (-).
- Será efetuada uma soma com todos os 20 números do jogo, e cada jogador deve escolher se o resultado dessa soma será um número par ou um número ímpar. A partir daí, cada jogador deve usar sua própria estratégia para que o resultado da soma corresponda ao que ele escolheu (número par ou número ímpar).
- Os dois jogadores se revezam, colocando sinais de mais (+) e de menos (-) aleatoriamente na frente dos números. O sinal e a posição em cada jogada são escolhidos pelo jogador da vez, de acordo com a sua estratégia.
- Depois de colocados todos os sinais, a soma é calculada (isto é, são efetuadas as adições e as subtrações).
- Vence o jogador que escolheu o resultado correto da soma (número par ou número ímpar).

Figura 1: Material para aplicação do jogo dos sinais
Fonte: Jogos/Jogos & Matemática.

Figura 2: Cartão de orientação do jogo dos sinais
O principal objetivo dessa atividade, que foi atingido após algumas jogadas, era instigar o estudante a se questionar por que o jogador que escolheu o resultado final da expressão como sendo um número parsempre vence e, consequentemente, levar o estudante a pensar e a concluir que a paridade do resultado final da expressão não depende das posições dos sinais de mais e de menos, só depende do número de inteiros ímpares no conjunto original de números. O entusiasmo na busca pela resposta foi geral!
Ao final dessa atividade, os estudantes ainda concluíram que tanto a soma de dois números pares como a soma de dois números ímpares é par, ao contrário da soma de um número par com um número ímpar, que é ímpar. Eles ficaram muito satisfeitos com suas próprias conclusões!



Figura 3: Aplicação do jogo dos sinais
Atividade 2: Trilha dos restos
Regras (Jogos/Jogos & Matemática):
- Número de jogadores: 4.
- Na primeira rodada, cada jogador locomove seu peão na trilha, de acordo com o número lançado no dado.
- A partir da segunda rodada, o jogador lança o dado, e o número sorteado será o seu divisor na operação a ser realizada.
- O dividendo dessa operação é o número da casa em que o peão parou.
- O resto dessa operação é o número de casas que o jogador deve andar.
- O jogador que, na sua vez, efetuar um cálculo errado, perde a sua vez de jogar.
- Será vencedor o jogador que sair primeiro da trilha.
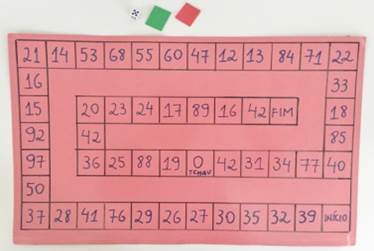
Figura 4: Material para aplicação da trilha dos restos
Fonte: Jogos/Jogos & Matemática.

Figura 5: Cartão de orientação da trilha dos restos
O objetivo dessa atividade, que foi alcançado com sucesso, era fixar, por meio das jogadas, os conceitos de divisor, dividendo e resto, além de relembrar algumas propriedades da divisão, entre elas o fato de que o resto não pode ser maior ou igual ao divisor. Os estudantes ficaram muito ansiosos para a chegada da vitória ao final da trilha!


Figura 6: Aplicação da trilha dos restos
Atividade 3: Jogo dos fatores

Figura 7: Material para aplicação do jogo dos fatores

Figura 8: Cartão de orientação do jogo dos fatores
Regras:
- Número de jogadores: 2.
- O primeiro jogador escolhe e marca um número do tabuleiro, e o segundo jogador marca todos os números do tabuleiro que são divisores desse número, exceto o próprio número já marcado pelo primeiro jogador;
- O segundo jogador agora escolhe e marca um novo número no tabuleiro, diferente dos números já marcados. O primeiro jogador marca então todos os divisores desse novo número, desde que eles já não tenham sido marcados.
- Os jogadores vão alternando assim as jogadas até marcarem todos os números do tabuleiro.
- A pontuação de cada jogador corresponde à quantidade de números que ele marcou no tabuleiro.
- Ganha o jogo quem tiver a maior quantidade de pontos.


Figura 9: Aplicação do jogos dos fatores
Os principais objetivos desse jogo, também alcançados com sucesso, eram relembrar e fixar o conceito de número primo, identificar os divisores e fatores de decomposição de um número e mostrar que os fatores de um número também são seus divisores. O anseio pela vitória estimulou o raciocínio dos estudantes e eles utilizaram as propriedades dos números primos como suas aliadas no tabuleiro.
Atividade 4: Jogo da escova diofantina

Figura 10: Jogo da escova diofantina

Figura 11: Cartão de orientação do jogo da escova diofantina
Regras:
- Número de jogadores: 4.
- Embaralhe as cartas e distribua três para cada jogador.
- Pegue quatro cartas e coloque-as desviradas no centro da mesa. O monte restante deixe de lado.
- O primeiro jogador deve procurar cartas em sua mão que, somadas com as cartas da mesa, totalizem 15, o que é chamado escova diofantina (Atenção: poderão ser utilizados, no máximo, dois números diferentes, o que significa que o jogador pode pegar duas ou três cartas da sua mão, desde que sejam iguais. Por exemplo: duas cartas de número 6 e três cartas de número 1);
- O jogador coloca à sua frente as cartas que pegou da mesa, assim como a carta da sua mão que permita a soma 15 com a face voltada para baixo. Caso ele não consiga pegar nenhuma carta da mesa, deve simplesmente descartar na mesa uma das cartas de sua mão.
- Quando os jogadores tiverem utilizado suas três cartas, uma nova mão de três cartas é distribuída, utilizando o monte que havia sido posto de lado inicialmente. A partida prossegue da mesma maneira até que as cartas terminem.
- Cada escova diofantina vale 1 ponto e vence a partida quem alcançar o maior número de pontos.


Figura 12: Aplicação da escova diofantina
O objetivo dessa atividade, que foi atingido ao término do jogo, era apresentar, de modo dinâmico e divertido, o conceito de equação diofantina linear. Ao final, os estudantes discutiram e concordaram que, abordado dessa maneira, o conceito de equação diofantina linear também pode ser apresentado para alunos do Ensino Médio.
Atividade 5: Jogo dos dominós
Regras:
- Número de jogadores: 2.
- Montar duas pilhas, cada uma delas com sete peças do dominó.
- Em cada jogada, o jogador da vez pode tirar quantas peças quiser, mas só de uma das pilhas.
- Perde o jogador que não conseguir fazer a sua jogada.

Figura 13: Material para aplicação do jogo dos dominós

Figura 14: Cartão de orientação do jogo dos dominós


Figura 15: Aplicação do jogo dos dominós
O objetivo dessa atividade, que foi conquistado após muitas jogadas, era estimular o estudante a criar uma estratégia vencedora utilizando o conceito de simetria. Essa atividade, em particular, causou grande euforia porque não era tão simples criar uma estratégia para alcançar a vitória, e os estudantes ficaram muito instigados. Ao finalizarmos essa atividade, eles observaram que o segundo jogador pode vencer esse jogo retirando exatamente o mesmo número de peças que o primeiro jogador acabou de retirar, mas da outra pilha. Desse modo, o segundo jogador sempre pode fazer a sua jogada, mas o primeiro jogador não. Todos os estudantes ficaram muito contentes com o aprendizado que adquiriram jogando!
Considerações finais
Ao final do minicurso, os estudantes responderam à seguinte avaliação:
- De qual atividade você mais gostou?
- De qual atividade você gostou menos?
- Observações gerais (sugestões, críticas...).

Figura 16: Avaliação do minicurso I

Figura 17: Avaliação do minicurso II
O nosso intuito com essa avaliação era verificar se o minicurso atingira seu objetivo, isto é, verificar se as atividades desenvolvidas contribuíram de algum modo para o aprendizado teórico, para a formação do pensamento crítico e para a futura prática docente dos estudantes. Após a leitura das respostas, constatamos o retorno positivo e ficamos muito satisfeitos com a nossa proposta.

Figura 18: Avaliação do minicurso III
De modo geral, as experiências relatadas através dessa avaliação comprovam como é importante para a construção da identidade profissional docente dos estudantes, futuros professores, articular os conhecimentos básicos, específicos e pedagógicos do currículo de formação deles com as práticas de ensino futuras.
Referências
BRASIL. Ministério da Educação. PNE. Disponível em: http://pne.mec.gov.br/. Acesso em: 11 jan. 2021.
CASTRO MONTEIRO, I. C. de; GASPAR, A. Um estudo sobre as emoções no contexto das interações sociais em sala de aula. Investigações em Ensino de Ciências, v. 12, nº 1, p. 71-84, 2007.
FOMIN, D.; GENKIN, S.; ITENBERG, I. Círculos matemáticos: a experiência russa. Trad. Valéria Magalhães Iório. Rio de Janeiro: Impa, 2010.
GIRALDO, V. et al. Práticas docentes compartilhadas: reconhecendo o espaço da escola na licenciatura em Matemática. SBEM - Educação Matemática em Revista, p. 52-60, 2016.
JOGOS. Jogos & Matemática, Rio de Janeiro. Disponível em: https://jogosmatunirio.wordpress.com/jogos. Acesso em: 12 jun. 2019.
KLEIN, F. Matemática elementar de um ponto de vista superior.v. I, parte I - Aritmética. Lisboa: Sociedade Portuguesa de Matemática, 2009.
______. Matemática elementar de um ponto de vista superior.v. I, parte II - Álgebra.Lisboa: Sociedade Portuguesa de Matemática, 2010.
______. Matemática elementar de um ponto de vista superior. v. I, parte III - Análise. Lisboa: Sociedade Portuguesa de Matemática, 2011.
STEWART, I. Almanaque das curiosidades matemáticas. Rio de Janeiro: Zahar, 2009.
______. Incríveis passatempos matemáticos. Rio de Janeiro: Zahar, 2010.
VYGOTSKY, L. S. Psicologia pedagógica. São Paulo: Martins Fontes, 2001.
Publicado em 26 de janeiro de 2021
Como citar este artigo (ABNT)
MELLO, Cristiane de; PEREIRA, Loisi Carla Monteiro; RAINHA, Marcelo Leonardo dos Santos. Práticas de ensino na formação do futuro professor de Matemática. Revista Educação Pública, v. 21, nº 3, 26 de janeiro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/3/praticas-de-ensino-na-formacao-do-futuro-professor-de-matematica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

