Reta Curiosa – uma abordagem com jogo sobre o aprendizado de reta, semirreta e segmento de reta
Teangela Lustosa Araújo
Pós-Graduanda em Ensino de Ciências e Matemática (IFPB/UAB)
Jefferson Dagmar Pessoa Brandão
Orientador, professor do curso de especialização em Ensino de Ciências e Matemática (IFPB/UAB)
É preocupante perceber o ensino perdendo sua qualidade em todas as suas modalidades. E a Matemática tem-se tornado uma dor de cabeça para os professores da disciplina. Druck (2003), ex-presidente da Sociedade Brasileira de Matemática (SBM) afirma: “a qualidade do ensino da Matemática atingiu, talvez, seu mais baixo nível na história educacional do país”. Pode-se perceber que a educação atual passa por um momento que exige muita reflexão acerca das possibilidades de um ensino mais expressivo, na tentativa de superar velhos processos de ensino que não atendem às expectativas dos professores e dos estudantes no processo ensino-aprendizagem.
De acordo com Groenwald e Timm (2007), para aprender Matemática é necessário o desenvolvimento do raciocínio lógico, e este deve ser estimulado no sentido de aumentar a criatividade do aluno na resolução de problemas matemáticos. Para isso, faz-se necessário que os educadores usem sua criatividade e motivação nos estudos dos conteúdos ministrados em Matemática. Dentro dessa problemática apresentamos os jogos matemáticos como facilitadores da aprendizagem, de desenvolvimento do raciocínio lógico, autoconfiança, organização, concentração – tudo isso utilizando o jogo lúdico.
Os Parâmetros Curriculares Nacionais (Brasil, 1998) consideram que os jogos matemáticos são eficientes na aplicação dos assuntos dados e entram como facilitadores no ensino-aprendizagem. Ainda nessa vertente, apontam que, por meio dos jogos, as crianças não apenas vivenciam situações que se repetem, mas aprendem a lidar com símbolos e a pensar por comparação (jogos simbólicos). O significado das coisas passa pelo imaginário das crianças, que se tornam produtoras de linguagem, criadoras de convenções, capacitando-se para submeter as regras e dar explicações.
No entanto, acreditamos que os livros didáticos deveriam trabalhar de forma mais direta no tocante aos jogos matemáticos, como uma forma de ajudar o professor no preparo de suas aulas, deixando-as mais criativas e atraentes para os estudantes, despertando assim o gosto pela Matemática.
Enquanto essa temática de jogos não se propagar mais, cabe ao professor desenvolver todo esse trabalho. O professor deve usar sua criatividade e buscar meios e materiais para confeccionar jogos para seus alunos. Os jogos lúdicos, como já foi apresentado aqui, ajudam o aluno na compreensão e assimilação dos conteúdos de forma prazerosa.
Diante dessa problemática, a pesquisa objetivou observar o desempenho dos estudantes do 6° ano do Ensino Fundamental na aprendizagem dos assuntos relacionados a reta, semirreta e segmento de reta com a utilização de jogos lúdicos e sem o uso deles como objetos facilitadores da aprendizagem.
Referencial teórico
Grando (1995) aponta que “a palavra jogo, do latim joco, significa, etimologicamente, gracejo e zombaria, sendo empregada no lugar de ludos, que representa brinquedo, jogo, divertimento e passatempo”.
Por meio desse passatempo, verifica-se que é mais acessível lecionar alguns conteúdos com os jogos. De fato, é uma conduta bem eficaz e serena expor uma temática tão mal enxergada pela maioria dos estudantes com leveza e abundante diversão.
Freire (1997, p. 28) afirma que “mulheres e homens, somos os únicos seres que, social e historicamente, nos tornamos capazes de aprender”. Por isso, somos os únicos em que aprender é uma aventura criadora, algo por isso mesmo muito mais rico do que meramente repetir a lição dada. Aprender para nós é construir, reconstruir, constatar para mudar, o que não se faz sem abertura ao risco e à aventura do espírito.
À vista disso, inserir algo de novo na sala de aula convoca copiosamente a concentração do estudante. A rotina não sugere nenhum atrativo; entretanto, distante dela pode-se vivenciar uma expansão infinita de aprendizado.
Do ponto de vista de Kishimoto (2011, p. 22), “ao permitir a manifestação do imaginário da criança, por meio de objetos simbólicos dispostos intencionalmente, a função pedagógica subsidia o desenvolvimento integral da criança”. Nesse sentido, qualquer jogo empregado na escola, desde que respeite a natureza do ato lúdico, apresenta caráter educativo e pode receber também a denominação geral de jogo educativo.
Com segurança, com base no entusiasmo que o mestre dispõe em contato do estudante um jogo que faz com que ele repare de forma confiante um certo tópico, é satisfatório e mais acessível até para o professor aplicar de forma excelente o que ele planeja, concebendo que o jogo, ao ser exposto pelo professor, faça com que fixe mais o conteúdo em sua mente. Quanto mais os estudantes treinarem, maior será a possibilidade de um aprendizado satisfatório.
O grau de obstáculo dos jogos ficará aplicado em combinação com a série dele, pois um jogo para o Ensino Fundamental não deve ter o mesmo nível de profundidade do Ensino Médio. Kishimoto (1994) ainda diz que, “se brinquedos são sempre suportes de brincadeiras, sua utilização deveria criar momentos lúdicos de livre exploração, nos quais prevalece a incerteza do ato e não se buscam resultados”. Porém, se os mesmos objetos servem como auxiliares da ação docente, buscam-se resultados em relação à aprendizagem de conceitos e noções, ou mesmo ao desenvolvimento de algumas habilidades. Nesse caso, o objeto conhecido como brinquedo não realiza sua função lúdica; deixa de ser brinquedo para tornar-se material pedagógico.
Rigorosamente, o material deixa de tornar-se um brinquedo e se transforma em uma grande ferramenta para o docente e, para os estudantes, uma metodologia prazerosa, que irá formar-se com diversão. Prontamente é que ficam vivenciando por meio dele, que eles se achem sendo capazes de uma afável evolução, diante da dificuldade do conteúdo exposto em sala. Dispondo o jogo de uma encantadora expansão do que o professor quer expor, eles alcançarão deter uma visão excelente e fixar com mais precisão. Logo, os estudantes, jogando entre eles, observarão que a sua aprendizagem da temática anda se concluindo de forma covenientemente mais descomplicada.
Na opinião de Piletti (1991), é primordial inserir atividades lúdicas em ambiente escolar, pois
a motivação é fator fundamental na aprendizagem. Sem motivação não há aprendizagem. Pode ocorrer aprendizagem sem professor, sem livro, sem escola e sem uma porção de outros recursos, mas mesmo que existam todos esses recursos favoráveis, se não houver motivação não haverá aprendizagem (Piletti, 1991, p. 63).
Doravante, nos anos iniciais do Ensino Fundamental, caso os professores conquistassem o interesse de seus estudantes a participar de uma interação com eles no decorrer de jogos e brincadeiras, eles lograriam se desenvolver sem temer em tal grau a Matemática. Os cálculos são inescusáveis em universalidade, contudo alguns jamais conseguem perceber isso. Os números acham-se manuseados integralmente em ascensão no nosso cotidiano.
Decroly (1978, p. 23) diz que
os jogos educativos não constituem senão que uma das múltiplas formas que podem tornar o material de jogo, mas têm por meta dominante a de fornecer à criança objetivos susceptíveis de favorecer a iniciação a certos conhecimentos e também permitir repetições frequentes em relação à retenção e às capacidades intelectuais da criança.
A sua constituição é que a criança detém a superior clareza de instruir teor diversificado se seus professores obtivessem constituir com que elas avolumem por meio dos jogos, captariam a complexidade da Matemática desvendada, assim mesmo contribuirá imensamente no transcorrer de seu itinerário. Deslindar esse arcano, que é tão despretensioso para minguados e de uma complexidade imprevisível para outros, é numerosamente respeitável.
Freire (1981, p. 54) sublima que
é fundamental, porém, é que a informação seja sempre precedida e associada à problematização do objeto em torno de cujo conhecimento ele dá esta ou aquela informação. Desta forma, se alcança uma síntese entre o conhecimento e o educador, mais sistematizado, e o conhecimento do educando, menos sistematizada, síntese que se faz através do diálogo.
Desse modo, o jogo não tem singularidade de domínio de transmudar as aulas mais dinâmicas, mas similarmente ser aproveitável para que os professores se façam capazes de identificar os essenciais obstáculos dos estudantes, servindo de diagnóstico de aprendizagem, devido ao fato de os jogos acharem-se apontados de sublime importância na aprendizagem dos estudantes. Apresentando com precisão, aqueles que seguidamente encontram uma dificuldade enorme de assimilar as temáticas desta disciplina, Matemática, essa metodologia diferencia o modo de levar o conteúdo e faz com que sua timidez diminua, visto que diversos estudantes se encontram envergonhados para elaborar perguntas, e suas dúvidas não são esclarecidas.
No jogo, alguns se identificam porque conseguem avistar e tocar ao mesmo tempo, noutro que para eles seria impossível a compreensão. Padecem quase que a asserção que eles mesmos, os estudantes, podem recolher suas próprias hesitações, tornando bem mais simples o trabalho dos professores e a compreensão dos complexos tópicos matemáticos incumbidos por parte dos estudantes.
Para Freire (1997, p. 103), “o professor que não leva a sério sua formação, que não estuda, que não se esforça para estar à altura de sua tarefa não tem força moral para coordenar as atividades de sua classe”.
O perceber do que faz bem, que motiva e faz acolitar e combater pelos objetivos é de suma relevância, se consumar na sua profissão, granjear o que tenciona ao fim de um dia de trabalho é demasiadamente prazeroso. Conceber o que gosta, atingir os seus objetivos com aquilo que tanto almeja é de uma satisfação indescritível.
Metodologia
Baseada em estudos teóricos sobre a temática, decidimos fazer uma coleta de dados nas duas turmas do 6º ano do Ensino Fundamental da Escola Dádiva Divina. Foi utilizado um questionário, que se encontra nos anexos. Na sala do 6º A aconteceu a explicação do conteúdo e na do 6º B foi apresentado um jogo: Reta Curiosa (que também está nos anexos), de acordo com o conteúdo que estava sendo abordado em sala de aula, reta.
O jogo foi criado pela professora das turmas em busca de uma metodologia em que os estudantes compreendessem melhor o conteúdo. O questionário contém cinco questões de múltipla escolha e uma questão discursiva; a pesquisa se tornou qualitativa e quantitativa.
Nas turmas do 6º ano foi apresentado um exercício sobre retas, a primeira forma de avaliar. Em seguida, apresentei o jogo e expliquei as regras. O jogo funciona assim: as fichas são distribuídas aos alunos com os desenhos de retas, segmentos de retas e semirretas. O verso de cada ficha contém a resposta de outra ficha. Depois de distribuídas, começamos perguntando ao aluno escolhido que responda que desenho está representado em sua ficha. Caso o aluno erre a resposta, pergunto aos outros alunos que figura é aquela apresentada pelo colega. Lembrando que atrás de cada ficha encontra-se o resultado das outras fichas. A ficha 1 contém a resposta da ficha 2; atrás da ficha 2 está a resposta da ficha 1 e assim por diante (Figura 1). Dessa forma, ficam facilitadas a resposta do aluno e a fixação do conteúdo.
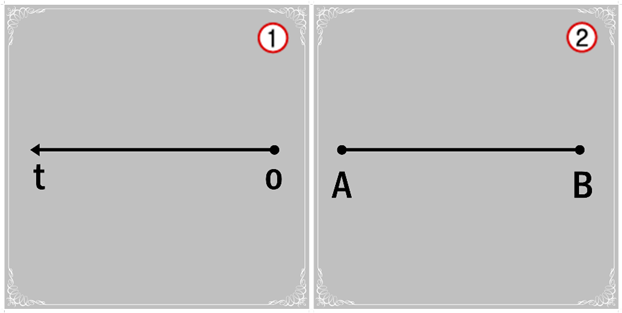
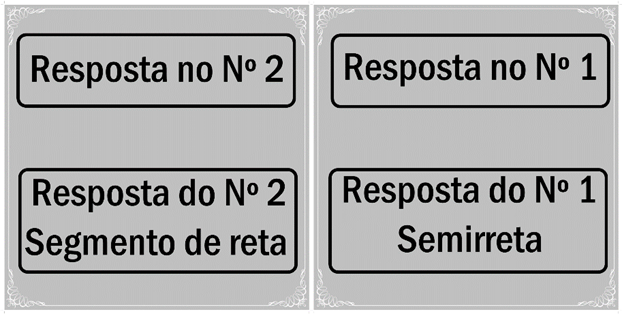
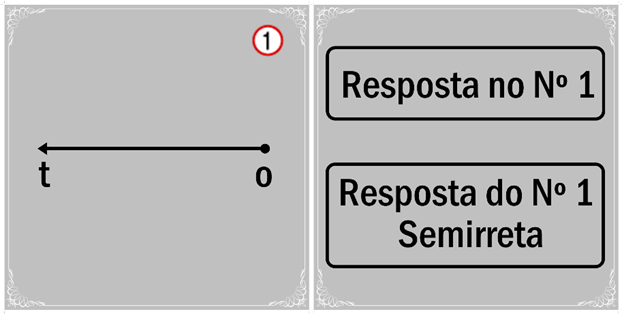
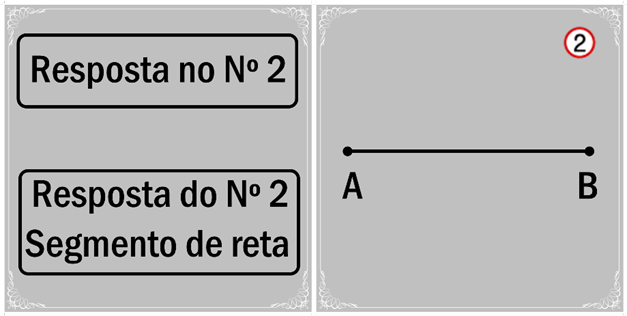
Figura 1: Fichas do jogo Reta Curiosa
Após a realização das duas metodologias, foi aplicado o questionário, em que se observaram as facilidades e dificuldades que cada um teve em compreender e resolver – tanto a primeira forma (explicação), na turma do 6º A, quanto a segunda (o jogo), na turma do 6º B. As atividades foram aplicadas individualmente no mês de maio de 2019; o jogo foi trabalhado, com todos os 40 alunos do 6º ano A e B, constando 20 alunos em cada turma.
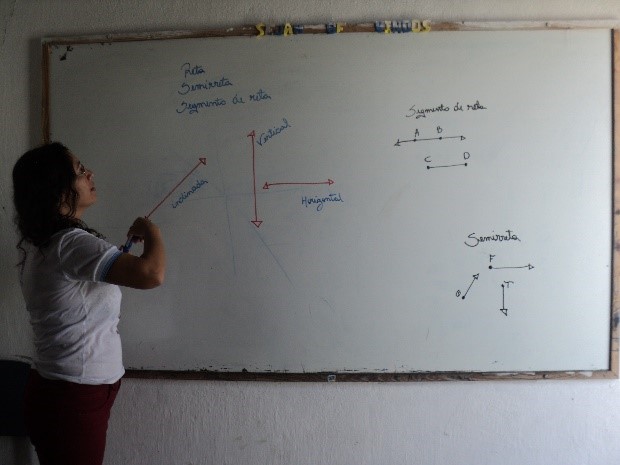
Figura 2: Explicando o conteúdo reta, semirreta e segmento de reta

Figura 3: Alunos participando do jogo da reta, semirreta e segmento de reta
Resultados e discussão
Os resultados a seguir foram construídos com base em informações coletadas no período citado com estudantes do 6º ano A e B da Escola Dádiva Divina, localizada em Santa Terezinha/PE. Segue depois disso uma discussão sobre os resultados, o que poderá contribuir para o aprofundamento da temática; esses dados foram coletados em um questionário aplicado em ambas as turmas. No Gráfico 1 encontra-se o percentual de aproveitamento dos alunos do 6° A o uso do jogo. No Gráfico 2 apresenta-se o resultado do 6° B com o uso do jogo.
No Gráfico 1 vê-se que 40% dos alunos do 6º ano A acharam difícil responder à atividade escrita, e 60% acharam fácil a resolução da atividade. Observa-se que parte do alunado sente dificuldade na resolução de questões matemáticas quando o professor apresenta em forma de exercício digitado. Cabe ao professor de Matemática preparar as novas gerações para o mundo em que terão que viver. Isso quer dizer proporcionar-lhes a aprendizagem para que adquiram as habilidades que serão indispensáveis para o desempenho de acordo com o avanço da tecnologia (Vitti, 1999, p. 103).

Figura 2: Frequência do aproveitamento no uso do jogo com os alunos do 6º A e 6º B (em %)
No Gráfico 2, tem-se que 10% dos alunos acharam difícil compreender o jogo enquanto 90% da turma do 6º B acharam fácil entender o conteúdo pelo jogo. Conforme os Parâmetros Curriculares Nacionais (PCN) (Brasil, 1998), uma vantagem relevante nos jogos é o desafio, o que faz com que os alunos sintam mais interesse e prazer pela disciplina. Portanto, os jogos são peças fundamentais para que a sociedade tenha indivíduos capazes de buscar soluções, enfrentar desafios, ser criadores de estratégias e se tornar pessoas críticas.
Em um estudo semelhante, Grando destaca que
a utilização dos jogos como metodologia para o ensino-aprendizagem na sala de aula vem acontecendo de forma lenta, pois os alunos precisam de tempo para se acostumar às novas metodologias. Torna-se necessário que o professor seja um mediador da construção da aprendizagem quando utilizá-los, pois deve ser criado um ambiente onde os alunos devem experimentar, ousar, desafiar e comprovar (Grando, 2000, p. 28).
Os resultados da questão subjetiva número 6, que foi incluída no questionário e que, em comparação com as respostas dos estudantes que não utilizaram o jogo, teve respostas mais completas e concisas, mostram que o jogo também contribuiu para melhorar a expressividade do estudante na escrita. O comentário dos estudantes sobre a importância de estudar esse conteúdo ficou claro em suas respostas; a maioria percebeu que em seu dia a dia as retas são aplicadas em sua diversidade em muitos locais e objetos do cotidiano de cada um dos alunos.
Considerações finais
Introduzir jogos no ensino e em especial na disciplina de Matemática torna as aulas mais dinâmicas e atraentes para os alunos. Também o professor pode utilizar o jogo como forma de diagnosticar as falhas na aprendizagem dos seus estudantes. A utilização do lúdico em sala de aula só vem somar no ensino-aprendizagem. Os jogos são um atrativo a mais para despertar a vontade de aprender Matemática por parte dos alunos.
Dada a importância do assunto, este trabalho retrata possíveis dificuldades na aprendizagem dos alunos no ensino da Matemática e em particular trabalhando com o conteúdo de retas em turmas de 6º ano do Ensino Fundamental. Os gráficos apresentados com resultados significativos de uso do jogo Reta Curiosa nos incentivam a utilizar a metodologia em outras turmas, diante dos níveis de porcentagem a favor da aprendizagem com o jogo.
Em função de tudo que foi apresentado, trazer o jogo para a sala de aula é algo muito relevante para que os alunos possam aprender cada vez mais; isso poderá desencadear maior envolvimento dos estudantes e, consequentemente, mudança de postura em relação ao ensino da Matemática. Também se configura uma mudança de postura na hora de apresentar a disciplina.
Referências
BORIN, J. Jogos e resolução de problemas: uma estratégia para as aulas de Matemática. 6ª ed. São Paulo: IME/USP, 1996.
BRASIL, Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais - Matemática. Brasília: MEC/SEF, 1998.
DRUCK, S. O drama do ensino da Matemática. Folha de São Paulo, Edição Especial, 2003.
FREIRE, Paulo. Pedagogia da Autonomia: saberes necessários à prática educativa. São Paulo: Paz e Terra, 1997.
______. Ação cultural para a liberdade. Rio de Janeiro: Paz e Terra, 1981.
GRANDO, Regina Célia. O jogo e a Matemática no contexto da sala de aula. São Paulo: Paulus, 2000.
GROENWALD, Claudia Lisete Oliveira; TIMM, Ursula Tatiana. Utilizando curiosidades e jogos matemáticos em sala de aula. Trabalho acadêmico. Porto Alegre, 2007.
KISHIMOTO, T. M. O jogo e a educação infantil. São Paulo: Pioneira, 1994.
PILETTI, Claudino. Didática geral. 14ª ed., São Paulo: Ática, 1991.
VITTI, C. M. Matemática com prazer a partir da História e da Geometria. 2ª ed. Piracicaba: Editora Unimep, 1999.
Questionário sobre reta
Escola: Dádiva Divina
Estado: Pernambuco
Disciplina: Matemática
Orientador: Jefferson Dagmar
Orientanda: Teangela Lustosa Araújo
Especialização em Ciência e Matemática
Questionário aplicado para os alunos do Ensino Fundamental II, para verificação da aprendizagem de reta, semirreta e segmento de reta
1 - O que é uma reta?
A ( ) Uma reta é um conjunto de pontos. Geometricamente, ela é representada como uma linha reta, isto é, que não faz curva alguma.
B ( ) Uma reta é um conjunto de pontos. Geometricamente, ela é representada como duas linhas retas, isto é, que não faz curva alguma.
C ( ) Uma reta é um conjunto de pontos. Geometricamente, ela é representada como uma linha reta, isto é, que faz curva.
D ( ) Uma reta é um conjunto de traços. Geometricamente, ela é representada como uma linha reta, isto é, que não faz curva alguma.
E ( ) N. D. A.
2 - Determinar o conceito de semirreta.
A ( ) As semirretas fazem parte dos estudos de Geometria e são retas que apresentam dois pontos de origem. Esse ponto indica seu início, no entanto elas não apresentam um fim, ou seja, são infinitas. Quando representadas, as semirretas são indicadas por uma seta de um dos lados, que demostra o sentido que não tem fim.
B ( ) As semirretas fazem parte dos estudos de Geometria e são retas que apresentam um ponto de origem. Esse ponto indica seu fim, no entanto elas não apresentam um fim, ou seja, são infinitas. Quando representadas, as semirretas são indicadas por uma seta de um dos lados, que demostra o sentido que não tem fim.
C ( ) As semirretas fazem parte dos estudos de Geometria e são retas que apresentam um ponto de origem. Esse ponto indica seu início, no entanto elas não apresentam um fim, ou seja, são infinitas. Quando representadas, as semirretas são indicadas por uma seta de um dos lados, que demostra o sentido que não tem fim.
D ( ) As semirretas fazem parte dos estudos de Geometria e são retas que apresentam um ponto de origem. Esse ponto indica seu início, no entanto elas não apresentam um fim, ou seja, são infinitas. Quando representadas, as semirretas são indicadas por uma reta de um dos lados, que demostra o sentido que não tem fim.
E ( ) N. D. A.
3 - Usando os conhecimentos prévios de retas, semirretas e segmentos de retas, indique o desenho correto de um segmento de reta.
A ( ) 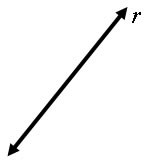
B ( ) 
C ( ) 
D ( ) 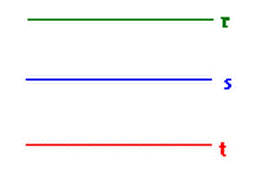
E ( ) N. D. A.
4 - Dentro do conteúdo abordado, marque a alternativa que melhor indica os tipos de retas.
A ( ) reta, semi e segmento
B ( ) paralelas, retas, inclinadas
C ( ) segmentos, paralelas e semi
D ( ) reta, semirreta e segmento de reta
E ( ) N. D. A.
5 - Dadas as alternativas abaixo, indique qual delas coincide com o que é segmento de reta.
A ( ) O segmento de reta é definido como uma da reta, o qual está delimitado por dois pontos.
B ( ) O segmento de reta é definido como uma parte da reta, o qual está delimitado por dois pontos.
C ( ) O segmento de reta é definido como uma parte da reta, o qual está delimitado por um ponto.
D ( ) O segmento de reta é definido como uma parte da reta, o qual está delimitado por dois pontos.
E ( ) N. D. A.
6 - Responda esta questão utilizando suas palavras sobre qual a importância de aprender o conteúdo abordado.
(Respostas individuais)
Publicado em 17 de agosto de 2021
Como citar este artigo (ABNT)
ARAÚJO, Teangela Lustosa; BRANDÃO, Jefferson Dagmar Pessoa. Reta Curiosa – uma abordagem com jogo sobre o aprendizado de reta, semirreta e segmento de reta. Revista Educação Pública, v. 21, nº 31, 17 de agosto de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/31/reta-curiosa-r-uma-abordagem-com-jogo-sobre-o-aprendizado-de-reta-semirreta-e-segmento-de-reta
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

