Aplicando ciência de dados educacionais para avaliar a influência da programação no progresso das notas do Ensino Médio
Ângelo Magno de Jesus
Doutor em Ensino de Ciência e Matemática (Unicsul), professor (IFMG - Câmpus Ouro Branco)
Alexandre Pimenta
Doutor em Engenharia Elétrica (UFMG), professor (IFMG - Câmpus Formiga)
Lilian Amaral de Carvalho
Doutora em Química (UFMG), professora (IFMG - Câmpus Arcos)
Natália Amaral Pereira de Souza
Licenciada em Computação (IFMG - Câmpus Ouro Branco)
É notável que há grande evolução da informática no decorrer dos anos, e a inserção tecnológica já faz parte do cotidiano dos indivíduos, sendo muitas vezes fundamental para necessidades básicas. Dentro do contexto escolar, há difusão do uso da tecnologia, de maneira que é comum o emprego de artefatos tecnológicos no cotidiano dos alunos, como smartphones, tablets e aplicativos, dentre outros. Porém a aplicação da tecnologia deve ir além do simples uso de softwares de instrução e equipamentos eletrônicos.
É preciso pensar na tecnologia de forma mais abrangente, entender como ela funciona e como a desenvolver para aplicá-la nas disciplinas escolares e nos problemas do dia a dia. Papert (1980) critica o modelo de ensino focado somente na instrução mediada por computador e defende que os computadores não devem programar os aprendizes e sim os aprendizes devem programar o computador. Portanto, a instituição de ensino deve fornecer amparo aos alunos para que a tecnologia seja usada a favor da educação, pela disseminação da linguagem de programação entre as disciplinas regulares.
Há necessidade de evolução na metodologia de ensino das escolas para que ela se desprenda das métricas tradicionais que já não se apresentam de forma tão eficiente devido à evolução desencadeada pela evolução tecnológica. A programação passa a exercer, na instituição de ensino, o papel de aparato metodológico e de disciplina de auxílio no desempenho dos alunos, fomentando as habilidades cognitivas dos estudantes e os auxiliando para que consigam compreender melhor as outras disciplinas.
Com o intuito de compreender se a presença da matéria de programação na grade regular afeta o desempenho dos alunos nas demais disciplinas, foi realizada uma análise para verificar como os alunos do 3° ano do Ensino Médio regular que possuem em sua grade disciplinar a programação apresentam desempenho acadêmico superior comparado com os alunos das outras turmas que não apresentam essa disciplina em sua grade. Nesse sentido, uma técnica de Ciência de Dados será aplicada com o objetivo de coletar possíveis evidências da influência da disciplina de programação na evolução das notas dos alunos em disciplinas básicas do Ensino Médio.
Para isso, foi realizado um estudo de caso com caráter quantitativo, em que um modelo matemático foi aplicado para medir a progressão média das notas dos alunos. Após isso, o algoritmo k-means foi processado com o objetivo de obter diferentes grupos de estudantes representando diferentes tipos de desempenho no progresso das notas. A partir desses grupos foi realizada análise para descoberta de padrões nos dados que poderiam indicar se há maior desempenho das turmas que tiveram aulas de programação em suas grades curriculares.
A importância da programação no ensino básico
Atualmente há uma grande dificuldade proeminente nos ambientes escolares, que é se adaptar aos recursos tecnológicos que estão cada vez mais presentes no cotidiano dos alunos. Pereira (2013) defende que as disciplinas que agregam o ensino da tecnologia deveriam vir junto com as disciplinas regulares, como Biologia e História, dentre outras, pois o ensino com apoio tecnológico reduz a evasão dos alunos e auxilia em seus desempenhos cognitivos.
As motivações de ensinar programação no ensino básico vão além de ensino de conceitos de tecnologia para serem usados no mercado de trabalho. Barr e Stephenson (2011) relatam que o Pensamento Computacional, que envolve a programação como componente, pode ser inserido no Ensino Fundamental como uma abordagem de resolução de problemas que pode ser empregada interdisciplinarmente no curso. Portanto, a disciplina de programação poderia ser atrelada ao currículo escolar como disciplina tecnológica que auxilia os alunos por meio de conceitos lógicos e desafios que estimulam o aprendizado. Nesse sentido, essa matéria teria o objetivo de elevar o desempenho estudantil e auxiliar o aluno em seu desenvolvimento durante o seu período de formação.
Garlet, Bigolin e Silveira (2016) salientam que a lógica da programação auxilia na sintaxe da linguagem, o que estimula a criatividade dos alunos e desenvolve diversas habilidades que não eram estimuladas no ensino tradicional. Há necessidade de evolução no ensino, pois o ensino tradicional já não se adapta ao contexto atual, sendo necessário que novas métricas sejam implementadas e novas disciplinas incluídas com o intuito de auxiliar o desenvolvimento dos alunos.
A Base Nacional Comum Curricular brasileira (Brasil, 2019, p. 539), no que diz respeito a competências da Matemática e suas Tecnologias no Ensino Médio, descreve que os alunos dessa modalidade de ensino devem desenvolver a "competência de utilizar conceitos iniciais de uma linguagem de programação na implementação de algoritmos escritos em linguagem corrente e/ou matemática". Além disso, a BNCC inclui o Pensamento Computacional (e, consequentemente, o aprendizado de conceitos de algoritmos e lógica de proclamação) como importante abordagem de resolução de problemas e meio de integração na sociedade digital.
Conforme Vargas (2012), por meio do raciocínio lógico, que pode se originar do aprendizado de programação, as pessoas podem desenvolver suas próprias formas de resolução de problemas e pensamentos originais sem se basear em conceitos predefinidos. Resnick et al. (2009) defendem que estudar programação de computadores pode ser uma maneira de aperfeiçoar habilidades de raciocínio lógico e, consequentemente, entender as ideias relacionadas ao Pensamento Computacional.
Há também a defesa de Alves (2016), que destaca que a programação, quando inserida no ensino regular, auxilia na resolução de problemas de diferentes áreas de conhecimento mesmo que não tenha ligação direta com as disciplinas. A programação também auxilia os alunos a estar mais bem preparados para o Ensino Superior, que muitas vezes solicita conhecimento dessa área para a atuação nas pesquisas acadêmicas.
Como pode ser observado da obra de Papert (1980), a informática, quando utilizada de forma construtivista, pode auxiliar os alunos a adquirir novos conhecimentos e a elevar a sua capacidade de se adaptar a diversas as disciplinas pelo raciocínio empregado para resolução de problemas e pelo constante uso da criatividade; por isso, a sua inserção no Ensino Médio é de extrema importância.
Dificuldades em inserir a disciplina de programação
Um dos grandes problemas destacados por Berssanete (2016) são as turmas extremamente grandes no Ensino Médio, pois para trabalhar a lógica da programação com computadores a instituição de ensino deve ter recursos suficientes para fornecer as ferramentas de ensino a todos os alunos. Essa dificuldade no Brasil é verificada principalmente no ensino público, em que as escolas possuem poucos recursos a serem utilizados e alguns que já estão desatualizados há anos, o que inviabiliza seu uso na disciplina de programação. Há necessidade de maior incentivo a essas aulas, por meio da divisão das turmas, da contratação de novos profissionais ou da aquisição de mais recursos que possibilitem o ensino de programação.
Berssanete (2016) também destaca que a dificuldade em Matemática acaba agindo diretamente sobre os alunos, pois a lógica de programação possui grande influência da lógica matemática, o que ocasiona grande dificuldade dos alunos em conseguir resolver os problemas propostos na disciplina.
Outro ponto relevante diz respeito aos profissionais da área, pois os que têm conhecimento de lógica de programação muitas vezes não estão preparados para lecionar as aulas, e muitos professores de Educação desconhecem o ensino da programação e, portanto, não estão aptos a ensinar a disciplina.
Todas essas dificuldades precisam ser trabalhadas para que as instituições de ensino possam ter boa estrutura para receber a disciplina de programação em sua grade e para que ela exerça a função de melhorar o desempenho dos estudantes, tornando o ensino mais interessante e estimulante para os alunos.
Influência da programação no desempenho escolar
Miranda (2016) destaca que muitos fatores podem influenciar o desempenho escolar, dentre eles a diferenciação da aplicação das disciplinas, ou seja, mudança nos recursos metodológicos de ensino ou a inserção de uma disciplina que está mais presente no cotidiano dos alunos, como é o caso da disciplina de programação.
Essa disciplina pode auxiliar no estímulo à criatividade, o que acaba sendo de grande auxílio nas outras disciplinas e pode levar à melhoria do desempenho escolar geral dos alunos. O raciocínio lógico, que também é desenvolvido na disciplina, traz maior estímulo na rapidez da captação dos dados, o que pode contribuir para melhor desempenho em Matemática.
Souza (2007) defende que há necessidade do apoio estrutural da escola para que a disciplina de programação seja bem desenvolvida com os alunos e consiga agir diretamente sobre o seu desempenho escolar, pois é com o apoio da escola e dos professores que há construção de um saber que se torna plausível e acessível a todos os alunos de forma a melhorar a educação.
Ciência de Dados Educacionais
Conforme Silva et al. (2017), a Ciência de Dados Educacionais pode ser entendida como a exploração de dados para aperfeiçoar a compreensão e a qualidade das experiências de aprendizagem. Isso é feito por meio da combinação de técnicas provindas da Estatística, Ciência da Computação e Educação. Esse campo pode envolver procedimentos de mineração de dados e de learning analytics. Nesse sentido, as instituições educacionais podem se beneficiar de técnicas de learning analytics para apoiar a tomada de decisão, identificar potenciais alunos "em risco", melhorar o sucesso do aluno (ou seja, taxas de retenção e formação), desenvolver políticas de recrutamento de alunos e ajustar o planejamento do curso, entre outras questões (Chatti et al., 2012).
Método de análise de dados empregado
A metodologia envolveu a coleta de dados a respeito das notas de nove turmas do Ensino Médio-Técnico Integrado: Técnico em Informática (3 turmas), Técnico em Administração (3 turmas) e Técnico em Metalurgia (3 turmas). Dessa forma, foram avaliadas as notas dos três anos correspondentes ao Ensino Médio das turmas ingressantes em 2013, 2014 e 2015. É importante observar que em cada ano houve o ingresso de uma turma de cada curso ofertado (Informática, Administração e Metalurgia). As turmas de Informática foram as únicas que envolveram a programação de computadores como componente curricular. Nesse sentido, três disciplinas principais são dedicadas completamente ao tema: Programação I - 1º ano, Programação II - 1º ano e Programação Web - 3º ano. Além disso, as disciplinas Projeto de Software I, Projeto de Software II, Banco de Dados, Robótica e Tópicos e Desenvolvimento de Software abordam o tema de forma indireta.
As notas coletadas passaram por análise de progressão com o objetivo de verificar se os estudantes estavam evoluindo em seu desempenho acadêmico. Dessa forma, considera-se que o aluno tem progresso quando apresenta sequência ascendente de notas. Portanto, analisaremos a progressão das notas aplicando a fórmula do termo médio (T.M.) da progressão aritmética (Equação 1), calculando assim o termo médio entre a primeira e última nota de cada disciplina.
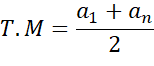
(1)
A fórmula foi ajustada a fim de considerar o aumento das notas, mas também penalizar por sua queda obtendo um resultado mais equilibrado. O cálculo da progressão média (P.M.) é apresentado na Equação 2. Essa equação considera a evolução do aluno em relação à sua primeira nota obtida na matéria. É importante observar que essa relação com a primeira nota foi estabelecida com o objetivo de não penalizar duramente o estudante quando sua pontuação no 3º ano de curso for inferior à nota do segundo, porém ainda superior ao 1º ano. Nesse sentido, ainda assim é possível observar progresso do aluno conforme suas notas.
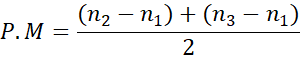
(2)
Por exemplo, os alunos x, y e z obtiveram as seguintes notas finais de Matemática durante os três anos do Ensino Médio:
x: n1 = 90; n2 = 95; n3 = 75.
y: n1 = 60; n2 = 70; n3 = 80.
z: n1 = 90; n2 = 70; n3 = 60.
Aplicando a fórmula da P.M., obtivemos os seguintes resultados:
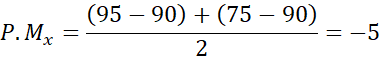
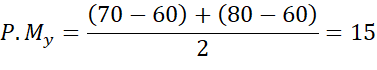
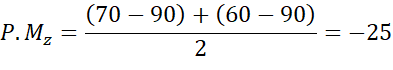
Com os resultados da progressão média dos alunos do exemplo acima, consegue-se visualizar uma regressão do aluno z, o avanço do aluno y e uma pequena queda do aluno x, que seria maior caso não fosse considerado também seu progresso. Dessa forma, a progressão média total foi calculada a partir das notas finais dos três anos de curso.
Após o cálculo dos pontos de progressão, as informações foram processadas pelo algoritmo de agrupamento de dados k-means. Como descrito por Palma (2018), algoritmos de agrupamento têm como objetivo segmentar dados em grupos de acordo com alguma função de dissimilaridade, visando obter ao mesmo tempo características parecidas dentro de seus grupos e características distintas entre eles. O objetivo dessa etapa foi agrupar os estudantes de diferentes cursos para identificar os padrões que cada grupo iria representar.
Conforme Palma (2018), o k-means é um algoritmo de agrupamento (clustering) de dados não hierárquico que utiliza técnica iterativa para particionar o conjunto de dados. O algoritmo busca minimizar a distância dos elementos de um conjunto de dados utilizando k centros de forma iterativa.
Considerando um conjunto de dados X = {p1, p2...pn} e uma distância d nesse conjunto, o k-means inicia-se com a escolha de k centroides (centros) {c1, c2...ck} para o agrupamento e depois associa cada ponto do conjunto X ao seu centro mais próximo segundo a distância d, formando, assim, k grupos Xi. O próximo passo do algoritmo é atualizar os centroides, originalmente calculando o ponto que minimiza a soma do quadrado da distância euclidiana, dE, entre ele mesmo e cada ponto do conjunto:
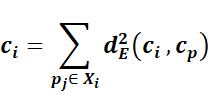
Esse ponto é justamente o centro de massa do grupo Xi e é dado por:
Ci = (pi1 + pi2 ...+ pin) Aqui, |Xi| corresponde à cardinalidade de Xi e pij ∈ Xi com j = 1, ...m com j = 1,... m (Pinele, 2017 apud Palma, 2018). No contexto deste estudo definimos k = 3. Optamos por esse valor pois era esperado que se formassem três grupos, cada um contendo provavelmente características de progressão alta, média ou baixa. O algoritmo foi configurado para escolher os pontos {c1, c2,...ck} para serem os centroides de cada grupo de forma aleatória. As dimensões dos pontos que representavam os alunos foram definidas como um vetor de valores de progressão de cada disciplina. Dessa forma, para cada grupo formado foram aplicados em uma etapa de pós-processamento algoritmos para:(1) cada grupo calcular as maiores médias de progressão por disciplina; e
(2) calcular a proporção de alunos de cada curso em cada grupo.
Resultados
Como informado, os dados foram computados para três turmas de cada curso avaliado. A Figura 1 mostra um gráfico das médias de todas as notas para cada ano das turmas avaliadas. Cabe observar que, para melhor entendimento da análise, quando uma turma é referenciada pelo ano, exemplo Metalurgia 2014, o texto na verdade se refere a turma do curso integrado egressa naquele ano - e não a um ano letivo específico do curso. Assim, MET2013(1) se refere à média das notas do 1º ano da turma do curso técnico em Metalurgia que formou em 2013, enquanto MET2013(2) se refere à média das notas do 2º ano dessa mesma turma. O termo INF se refere às turmas do curso técnico em Informática e ADM se refere às turmas do curso técnico em Administração. A Tabela 1 mostra a variância entre esses valores. Como pode ser observado, o maior valor de variância ocorreu na turma de Administração 2015. Isso pode ter ocorrido devido à média de notas muito alta no 3º ano em relação aos dois anos anteriores. Ocorre algo similar com a turma de Administração 2013, porém em relação à nota do 2º ano. E a terceira maior variância ocorreu para a turma de Informática 2014, justamente porque a nota no 1º ano era mais elevada do que nos anos seguintes. Apesar disso, em geral os valores de variância ficaram próximos de 1, o que indica que não houve grandes discrepâncias nas médias das notas entre os anos.
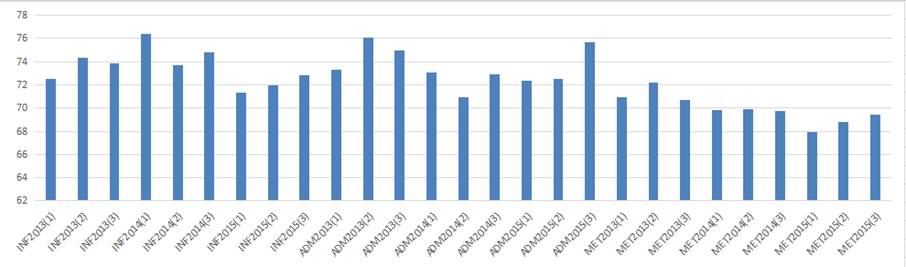
Figura 1: Média das notas por ano para cada turma analisada.
Tabela 1: Variância das médias das notas por ano para cada turma
Turma |
Variância |
Informática 2013 |
0,92 |
Informática 2014 |
1,80 |
Informática 2015 |
0,54 |
Administração 2013 |
1,96 |
Administração 2014 |
1,44 |
Administração 2015 |
3,48 |
Metalurgia 2013 |
0,63 |
Metalurgia 2014 |
0,00 |
Metalurgia 2015 |
0,59 |
A Tabela 2 apresenta a distribuição, por cursos, dos alunos em estudo. Cabe observar que os dados foram filtrados com o objetivo de eliminar estudantes desistentes, repetentes e outros elementos que poderiam prejudicar a consistência da análise.
Tabela 2: Quantidade de alunos analisados por turma
Curso/Turma |
1 |
2 |
3 |
Total |
Informática |
25 |
29 |
21 |
75 |
Administração |
23 |
37 |
28 |
88 |
Metalurgia |
29 |
29 |
27 |
85 |
A Tabela 3 mostra as médias por disciplina computadas para cada grupo obtido na aplicação do k-means. Como pode ser observado, o Grupo 2 obteve as maiores médias em todas as disciplinas. O Grupo 1 obteve a menor pontuação em quase todas as matérias, exceto Física, Geografia e Língua Estrangeira, disciplinas em que o Grupo 3 ficou com a menor pontuação.
Tabela 3: Resultado do k-means: média de pontuação de progressão obtidas para cada agrupamento
Disciplina |
Grupo 1 |
Grupo 2 |
Grupo 3 |
Biologia |
1.86 |
4.47 |
4.01 |
Educação Física |
-5.10 |
7.19 |
-0.43 |
Filosofia |
-7.33 |
0.64 |
0.54 |
Física |
1.49 |
4.09 |
1.05 |
Geografia |
4.73 |
7.37 |
1.39 |
História |
-10.50 |
7.06 |
3.79 |
Língua Estrangeira |
-0.33 |
6.70 |
-1.30 |
Português |
-4.97 |
1.25 |
-3.51 |
Matemática |
-3.14 |
2.58 |
-1.71 |
Química |
0.78 |
3.88 |
1.93 |
Sociologia |
-1.76 |
3.85 |
1.46 |
Os dados da Tabela 4 mostram a proporção de alunos de cada curso em cada grupo obtido pelo k-means. Cabe observar que os Grupos 1, 2 e 3 agruparam ao todo 90, 53 e 105 alunos, respectivamente.
Tabela 4: Resultado do k-means: proporção de alunos dos cursos por grupo (cluster)
Curso |
Grupo 1 |
Grupo 2 |
Grupo 3 |
Informática |
44% |
27% |
29% |
Administração |
28% |
18% |
54% |
Metalurgia |
38% |
20% |
42% |
Discussão
Pode ser observado que o curso de Informática foi o que obteve a maior proporção de alunos (27%) no Grupo 2, mas também obteve maior proporção de alunos no Grupo 1. As turmas dos demais cursos técnicos apresentaram mais alunos no Grupo 3, o que indica menor variação das notas ao longo dos anos.
Os dados obtidos não indicaram evidências de que a presença das disciplinas de programação na grade curricular promova aumento geral no rendimento acadêmico dos alunos. Apesar de a maioria dos alunos do grupo de maior progressão média ser do curso técnico de Informática, que apresenta disciplinas de programação na grade, a maior proporção de alunos do grupo de menores progressões médias também é desse curso. Esse resultado pode indicar uma polarização dos valores de progressão da turma de Informática, com parte significativa dos alunos apresentando progressões relativamente altas e parte ainda maior apresentando redução das notas.
É importante observar que este estudo apresenta limitações que precisam ser levadas em consideração. Nesse sentido, cabe registrar que, por se tratar de um ambiente não controlado, inúmeras variáveis não podem ser levadas em consideração na análise de dados: a motivação intrínseca dos alunos para estudar programação; a base educacional dos alunos antes de entrarem na instituição de ensino, o que é influenciado pelo processo de vestibular, no qual um curso técnico pode ser mais concorrido que os outros; o nível de dificuldade das disciplinas da matriz técnica do curso – as matérias técnicas de um curso X podem exigir mais tempo dos alunos que as de um curso Y, o que pode prejudicar seu desempenho; as metodologias de ensino e o nível de exigência de conteúdo por parte dos professores das disciplinas, pois as disciplinas da matriz propedêutica nem sempre poderiam ser ministradas pelos mesmos professores nas três turmas mencionadas. Além disso, este estudo assume que o progresso do aluno se dá pela evolução de suas notas escolares, o que nem sempre representa a realidade.
Assim, sugere-se, para trabalhos futuros, a investigação dos seguintes componentes do processo de ensino-aprendizagem nas disciplinas de programação da escola pesquisada:
§ Interdisciplinaridade: o ensino da disciplina de programação pode estar acontecendo sem que haja conexão com outras áreas do saber, o que impacta na capacidade do aluno de correlacionar e aplicar o que está sendo ensinado nas outras matérias;
§ Ensino pela resolução de problemas: o foco das aulas pode estar sendo dado no entendimento da tecnologia (ferramentas de programação) e não no raciocínio lógico e nos métodos sistemáticos para resolver problemas. Nesse sentido, os alunos estariam aprendendo mais por decorar conceitos do que por aplicar estratégias de resolução de problemas;
§ Utilização de metodologias de ativas de aprendizagem: como informado, os alunos podem estar aprendendo somente por repetir de forma automática os conceitos de programação. O uso de metodologias ativas de aprendizagem pode tornar os alunos protagonistas de seu próprio aprendizado e mostrar caminhos para aplicar a programação em outras áreas do saber;
§ Motivação dos estudantes: os estudantes podem estar sem interesse na disciplina devido aos motivos já citados ou por estarem sobrecarregados. No último caso, é preciso investigar qual seria a carga horária ideal para inserir a disciplina de programação de computadores na matriz do estudante e o nível de exigência que a disciplina fará dos alunos.
Considerações finais
A pesquisa não encontrou evidências concretas de que a presença de disciplinas de programação na grade dos cursos técnicos pode contribuir para a melhoria do desempenho acadêmico dos alunos. Entretanto, não foram avaliadas as formas como elas foram trabalhadas nem outros fatores que podem influenciar no desempenho acadêmico, como motivação e sobrecarga de professores e alunos; interdisciplinaridade; incentivos à proatividade e ao protagonismo dos alunos; uso de metodologias ativas; conhecimentos prévios; apoio da família; vulnerabilidade social etc. Sugere-se a pesquisa desses e de outros fatores em trabalhos futuros.
É importante observar que este estudo não é (e não pretende ser) conclusivo, não só pelas limitações metodológicas que foram descritas anteriormente como também (e principalmente) pela grande complexidade que envolve temas que incluem influências de aprendizado e do pensamento típico de umas disciplinas sobre as outras. Nesse sentido, este tema exige um número dispendioso de estudos envolvendo Ciências Cognitivas, Ciências Sociais, Neurociência e Educação. No entanto, os resultados deste estudo podem contribuir metodologicamente para a área de pesquisa e incentivar trabalhos futuros.
Referências
ALVES, N. D. C. Ensino de computação de forma interdisciplinar em disciplinas de História no Ensino Fundamental: um estudo de caso. Revista Brasileira de Informática na Educação, v. 24, nº 3, p. 31-46, 2016.
BARR, Valerie; STEPHENSON, Chris. Bringing computational thinking to K-12: what is Involved and what is the role of the computer science education community? Acm Inroads, v. 2, nº 1, p. 48-54, 2011.
BERSSANETTE, João Henrique. Ensino de programação de computadores: uma proposta de abordagem prática baseada em Ausubel. 2016. 145f. Dissertação (Mestrado em Ensino de Ciência e Tecnologia), Universidade Tecnológica Federal do Paraná, Ponta Grossa. 2016.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC/SEB, 2019. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: nov. 2019.
CHATTI, M. A. et al. A reference model for learning analytics. International Journal of Teaching Enhanced Learning, v. 4, nº 5/6, p. 304-317, 2012.
GARLET, D.; BIGOLIN, N. M.; SILVEIRA, S. R. Uma proposta para o ensino de programação de computadores na Educação Básica. Santa Maria: Universidade Federal de Santa Maria, Departamento de Tecnologia da Informação, 2016. Disponível em: https://repositorio.ufsm.br/bitstream/handle/1/12961/TCCG_SIFW_2016_GARLET_DANIELA.pdf?sequence=1&isAllowed=y. Acesso em: set. 2020.
MIRANDA, Pauline Vielmo. A influência do ambiente escolar no processo de aprendizagem de escolas técnicas. In: FÓRUM INTERNACIONAL DE EDUCAÇÃO, 2, 2016. Anais... Santa Cruz do Sul: Universidade Santa Cruz do Sul, 2016.
PALMA, Luann Faria. Agrupamento de dados: k-médias. 2018. 45f. Trabalho de Conclusão de Curso, Universidade Federal do Recôncavo da Bahia, Cruz das Almas, 2018.
PAPERT, S. Mindstorms: children, computers and powerful ideas. New York: Basic Books, 1980.
PEREIRA, L. Escolas defendem ensino de programação a crianças e adolescentes. Olhar Digital, 2013. Disponível em: http://olhardigital.uol.com.br/jovem/digital_news/noticias/escolas-defendem-ensino-de-programacao-a-criancas-e-adolescentes. Acesso em: out. 2020.
RESNICK, M. et al. Scratch: programming for all. Communications of ACM, v. 52, nº 11, p. 60–67, 2009. Disponível em: https://web.media.mit.edu/~mres/papers/Scratch-CACM-final.pdf. Acesso em: out. 2020.
SILVA, L. A. et al. Ciência de dados educacionais: definições e convergências entre as áreas de pesquisa. In: CONGRESSO BRASILEIRO DE INFORMÁTICA NA EDUCAÇÃO - WCBIE 2017, 6, Workshops, 2017. Anais... Recife: SBC, 2017.
SOUZA, S. E. O uso de recursos didáticos no ensino escolar. Arq. Mudi., v. 7, nº 11, p. 110-114, 2007.
VARGAS, M. N. Utilização da robótica educacional como ferramenta lúdica de aprendizagem na Engenharia de Produção: introdução à produção automatizada. In: CONGRESSO BRASILEIRO DE EDUCAÇÃO EM ENGENHARIA, 40, 2012. Anais... Belém: Abenge, 2012.
Publicado em 31 de agosto de 2021
Como citar este artigo (ABNT)
JESUS, Ângelo Magno de; PIMENTA, Alexandre; CARVALHO, Lilian Amaral de; SOUZA, Natália Amaral Pereira de. Aplicando ciência de dados educacionais para avaliar a influência da programação no progresso das notas do Ensino Médio. Revista Educação Pública, v. 21, nº 33, 31 de agosto de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/33/aplicando-ciencia-de-dados-educacionais-para-avaliar-a-influencia-da-programacao-no-progresso-das-notas-do-ensino-medio
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

