Matemática e Música no Ensino Médio: duas linguagens e uma sinfonia
Andréia Miranda dos Santos Vasconcelos
Licencianda em Matemática (IFMG - Câmpus São João Evangelista)
Lucas da Silva Vasconcelos
Licenciando em Matemática (IFMG - Câmpus São João Evangelista)
Sandra Regina do Amaral
Doutora em Educação (UFU), professora (IFMG - Câmpus São João Evangelista)
Tiago de Oliveira Dias
Mestre em Matemática (UFV), professor (IFMG - Câmpus São João Evangelista)
Wálmisson Régis de Almeida
Mestre em Matemática (UFSJ), professor (IFMG - Câmpus São João Evangelista)
Os conhecimentos matemáticos são úteis às mais corriqueiras atividades humanas. Praticamente tudo ao nosso redor envolve números, cálculos, formas geométricas, noções de quantidade e de espaço, seja na medida do pão, na compra no mercado, ao olhar as horas, dividir um lanche, pagar ou receber troco. Relação parecida com a que modela as leis, formas e melodias musicais, que se apresentam ao ouvir-se o rádio do vizinho ligado, o som dos pássaros ou o toque do celular. Revela-se assim um dueto que pode, por um lado, alargar as experiências musicais e, por outro, contribuir para a superação do estigma de que a Matemática é ciência inatingível para boa parcela da população.
Nem todos percebem que há uma sintonia entre essas duas teorias. A Música não traz consigo apenas o potencial de expressão da arte, mas também os saberes da ciência, principalmente envolvendo a Física e a Matemática. Algumas pessoas que demonstram afinidade com a Música e querem aprender a cantar ou tocar só percebem a necessidade dos saberesmatemáticos quando iniciam os estudos em Teoria Musical (TM). Nesse momento, a relação de sinergia entre essas duas áreas pode despertar o prazer pela Matemática, justamente o intuito deste trabalho.
Na escola, Matemática e Música, duas linguagens mundialmente conhecidas, poderiam ser integradas, possibilitando a ampliação do pensamento musical e matemático do aluno, favorecendo assim o aprendizado de alguns alunos que têm chegado ao Ensino Médio com dificuldades em conceitos como multiplicação, divisão, fração e número na forma decimal. Mas elas ainda se mantêm distantes, talvez pela falta de professores que dominam a TM, principalmente os de Matemática, dificultando a integração e para uso como instrumento educacional/pedagógico.
Neste sentido, este estudo se justifica ao propor videoaulas de iniciação musical com elementos matemáticos, possibilitando que o aluno consiga utilizar variados conceitos, de uma forma mais ilustrada, por meio da TM; além disso, existe a possibilidade de se trabalhar a matematização do processo de produção de sons em instrumentos de cordas e de tubos, inserida no contexto do ensino de acústica. Deste modo, a Física, aliada à Matemática e à TM, potencializaria conceitos normalmente trabalhados nos anos finais do Ensino Fundamental e no Ensino Médio.
Tal cenário revela uma conciliação a ser explorada e a seguinte questão norteadora do estudo: seria possível a conciliação “Música e Matemática” no ensino de conceitos matemáticos no Ensino Médio? Acredita-se que experiências de conciliação irão ajudar no ensino da Matemática e na aplicabilidade de seus conceitos de forma mais prazerosa e contextualizada.
Estabeleceu-se então por objetivo geral, analisar a possibilidade de conciliação entre Música e Matemática no processo de ensino. E como objetivos específicos:(1) elaborar videoaulas para ampliação do conhecimento sobre a relação entre Teoria Musical, Matemática e a Física na produção de sons; (2) validar a proposta apresentada nas videoaulas com professores de Matemática e Arte que atuam no Ensino Médio; (3) avaliar, a partir da perspectiva dos professores, os impactos das videoaulas para ampliação do conhecimento nos conteúdos acadêmicos.
Entende-se que cada aluno aprende de uma forma diferente, sendo um dos caminhos o entendimento da TM e suas relações com os conhecimentos matemáticos, dentre as quais estão as fórmulas de compasso, os compassos simples e compostos, as figuras musicais, o solfejo, as divisões e subdivisões, etc., que podem favorecer, por exemplo, o ensino de operações com frações, números decimais, contagem de tempos, agrupamentos de tempo, e também as relações físico-matemáticas e suas equações na produção de sons em instrumentos de corda e sopro, que podem também ser exploradas nesse mesmo interim para aprofundar essas relações.
Fundamentação teórica
As ideias matemáticas estão presentes nas formas do fazer e do saber, “comparecem em toda a evolução da humanidade, definindo estratégias de ação para lidar com o ambiente, criando e desenhando instrumentos para esse fim, e buscando explicações sobre os fatos e fenômenos da natureza e para a própria existência” (D’Ambrosio, 1999, p. 97). Nesse sentido, o conhecimento aprofundado e global do passado nos permite entender o presente, apresentando-se como pressuposto para inovações e ideias criativas, e sobretudo para soluções que ofereçam um futuro melhor ao mundo (D’Ambrosio, 1997, p. 113).
A Educação Matemática “implica olhar a própria Matemática do ponto de vista do seu fazer e do seu pensar, da sua construção histórica e implica, também, olhar o ensinar e o aprender Matemática, buscando compreendê-los” (Medeiros, 1987, p. 24). É importante que o aluno entenda que a Matemática é uma construção cultural, criada nos diferentes tempos e espaços para resolver problemas relevantes da vida em sociedade, pois se o aluno a entende como algo palpável, fica mais cativado com o conteúdo, pois quanto menos abstrato, maior a possibilidade de aprendizagem (D’Ambrosio, 2000).
Flemming, Luz e Mello (2005) explicam que a Educação Matemática busca, a partir de referenciais teóricos consolidados, análises, soluções e alternativas que inovem o ensino da Matemática. Tais mudanças ajudariam a estabelecer uma nova rotina, diferente da estabelecida por uma linha tradicional de educação, possibilitando a percepção de que a Matemática faz parte do cotidiano de todos. Seguindo este mesmo pensar, Pires (2000) afirma que o aluno deve solucionar problemas para obter um conhecimento elevado e compreender as situações, não ficando apenas nos conhecimentos formais como memorização de fórmulas, de definições, ou de caminhos mais fáceis para chegar a resultados de exercícios.
Posicionando-se contra a reprodução mecânica no ensino da Matemática, D’Ambrosio (1997, p. 105) afirma que “a aparente aquisição de uma rotina de execução conduz a falta de criatividade e consequentemente a ineficiência”, recomendando que o professor tome o cuidado de não ensinar algo da mesma forma que ensinou há anos atrás, como se a Matemática fosse sempre a mesma. Vale lembrar ainda “que não é possível ao(à) educador(a) desconhecer, subestimar ou negar os “saberes de experiência feitos” com que os educandos chegam à escola” (Freire, 1997, p. 31), pois a relação do que é ensinado com o dia a dia do aluno é primordial para a construção do conhecimento.
Evidencia-se, assim, que a perspectiva tradicional dos processos de ensinar e aprender se tornou obsoleta e desinteressante aos alunos, fazendo com que o professor passe “a ser continuamente desafiado a atualizar-se e tentar ensinar de um modo diferente daquele vivido em seu processo de escolarização e formação profissional” (Fiorentini, 2008, p. 45). Dentre as sequelas de uma prática educativa arcaica, pode-se destacar o fato de a Matemática ter se tornado a mais temida das matérias escolares, e consequentemente, a maior responsável pela repetência e evasão escolar (Lorenzato, 2010).
Entende-se que não cabe à escola ensinar conteúdos prontos e acabados que podem ser aplicados e reaplicados em atividades simuladas. A escola precisa ser comprometida com a cidadania, com a formação de seres humanos plenos e pensantes, que terão maiores oportunidades de usar seus conhecimentos em situações reais de vida nesses tempos modernos (Freire, 1997). Por meio da música, é possível estabelecer relações cognitivas e afetivas desde o nascimento (Brito, 2003). Nesse sentido, aposta-se na conciliação entre a Matemática e a Música, já que a inteligência congrega em si múltiplas capacidades que se encontram intimamente ligadas à sabedoria popular, favorecendo a construção de significados por meio de canais heterogêneos, que proporcionam maior diversidade de experiências (Gardner, 1995).
Muitos manifestam não gostar da Matemática por considerá-la difícil. Por outro lado, o gosto pela Música seria quase unânime, e, por isto, essa conciliação poderia ampliar o interesse e revelar mais uma aplicação para os conhecimentos matemáticos (Morais, 2008). Existem diversas definições para Música, mas sua relação com a Matemática fez com que alguns autores dessem a ela o status de ciência, sendo então considerada simultaneamente ciência e arte: “as relações entre os elementos musicais são relações matemáticas e físicas” e “a arte manifesta-se pela escolha dos arranjos e combinações” (Penna, 1990, p. 22).
Segundo Abdounur (2006), a origem dessa relação está associada a Pitágoras (séc. VI a.C.), que investigou através de um instrumento musical de apenas uma corda (monocórdio) a relação entre o tom musical e o comprimento da corda vibrante, além de perceber que o som das batidas de martelos numa bigorna variava conforme o peso do martelo e que as batidas em uma urna de água também variavam conforme a quantidade de água, descobertas de grande valia para o entendimento dos intervalos musicais e seu registro, por meio do uso de números decimais. Enfim, a partir das relações matemáticas é possível definir a escala musical, explorar vibrações sonoras e construir combinações harmoniosas (Ratton, 2003).
Tomando por base essa intrincada relação, defende-se então, que a partir dos conhecimentos musicais, é possível ensinar com alegria, aguçar o olhar curioso e estabelecer uma relação mais prazerosa com os saberes matemáticos (Camargos, 2010). Uma reflexão que contribui para a percepção do potencial de levar a Música para o ambiente escolar, principalmente vinculado ao ensino da Matemática, pois os alunos, além de dominar os conteúdos matemáticos, podem ampliar suas habilidades, exercitando a linguagem musical.
O raciocínio matemático se apresenta na Música desde as primeiras aulas teóricas, na qual o aluno tem a noção dos elementos musicais, tais como ritmo, compasso, fórmula de compasso e figuras musicais, para os quais é necessário conhecer os valores fracionários e seu respectivo número na fórmula de compasso, que também deverá ser somado, subtraído, dividido ou multiplicado em frações ou decimais (Bona, 2004).
Reforçando a relevância da temática, tal conciliação encontra-se devidamente registrada na Base Nacional Comum Curricular – BNCC (Brasil, 2018), trazendo à tona que a compreensão das propriedades sonoras é parte do arcabouço de conhecimentos que a escola deve levar à vida do cidadão em formação, ao orientar objetivos de aprendizagem e desenvolvimento nessa área associados tanto à Matemática, quanto às Artes, às Linguagens e às Ciências. O documento descreve habilidades a serem assimiladas pelos discentes nas diferentes etapas da Educação Básica, conforme pode-se ver no Quadro 1.
Quadro 1: Habilidades relacionadas à música na BNCC
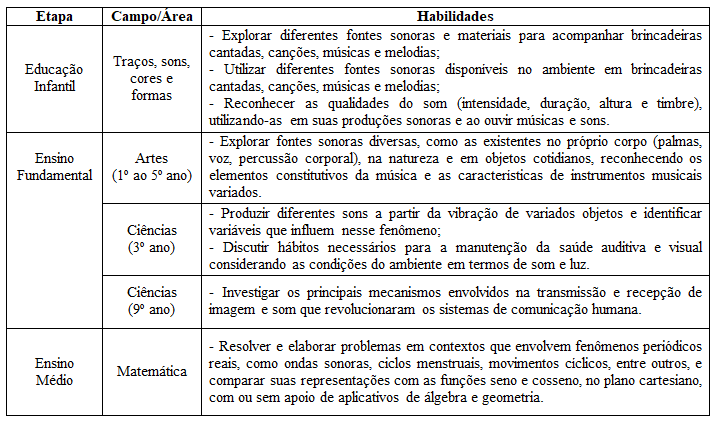
Além das habilidades apresentadas na Figura 1, encontra-se no texto da BNCC (Brasil, 2018) várias outras menções aos termos som e ondas sonoras. De modo genérico, o som pode ser definido como qualquer onda longitudinal, ou seja, ondas nas quais as oscilações acontecem na direção de sua propagação (Halliday, 2016). O som (onda invisível) é a principal matéria da Música: ainda que não seja visto, ele dá corpo e rompe o silêncio, tornando o conhecimento palpável (LINO, 2006), o que reforça a defesa de que cabe, inclusive na Educação Matemática, trabalhar conhecimentos pertinentes à Música.
Entende-se assim que estas duas linguagens podem se interligar, possibilitando uma prática educativa que favoreça a ampliação do pensamento musical, matemático e físico, permitindo que o aluno se aproprie dos conceitos matemáticos de uma forma mais ilustrada.
Metodologia
Adotou-se um estudo de abordagem qualiquantitativa dos dados. Isso tornou possível, por um lado, associar e comparar os dados recolhidos valorizando os aspectos científicos no que diz respeito à análise através de recursos e técnicas estatísticas, mas também apresentar opiniões e informações de modo descritivo, permitindo replicar inclusive, em alguns momentos, a fala do participante na íntegra (GIL, 2002).
Quanto aos objetivos, a pesquisa foi exploratória e descritiva, sendo desenvolvido o levantamento bibliográfico e o aprofundamentodas informações no âmbito da práticapor meio de videoaulas, o que permitiu levantar opiniões de professores de Matemática e Música, que atuam ou atuaram no Ensino Médio, quanto à conciliação dessas duas linguagens. Os participantes foram abordados por intermédio de recursos tecnológicos (via e-mail e WhatsApp), mantendo assim a orientação atual do Ministério da Saúde de isolamento social devido ao momento de pandemia.
Os participantes foram convidados a assistir às videoaulas, analisar uma lista avaliativarelativa ao conteúdo e responder a um questionário enviado via Google Forms. O formulário apresentou em sua parte inicial o Termo de Consentimento Livre e Esclarecido (TCLE) e a indicação de apreciação de 5 videoaulas de conciliação entre Matemática, Física e Música, com duração aproximada de 50 minutos. A sequência abordou os seguintes conceitos:
- Resumo do Trabalho e introdução ao som (ondas sonoras, qualidades do som);
- Teoria musical: figuras musicais, pentagrama, compasso, fórmula de compasso, e exemplos de operações com frações na partitura musical;
- Atividades com partitura musical;
- Introdução à acústica: fontes de sons musicais, produção de sons em cordas e tubos, velocidade do som, e equações;
- Resolução de atividades envolvendo acústica.
Buscou-se utilizar nas videoaulas linguagem adequada ao Ensino Médio, sendo este o público-alvo da proposta. Porém, a metodologia de validação a priori (Giordan; Guimarães, 2013), objeto de análise deste estudo, foi desenvolvida com quatorze professores de Matemática e um de Música, tornando possível analisar a capacidade de conciliação “Música e Matemática” no processo de ensino de Matemática para o Ensino Médio na perspectiva dos docentes. Quanto ao processo de análise, o tratamento de dados se deu por meio de gráficos e tabelas, que permitiram a tabulação e representação que, junto com o texto, apresentaram os resultados obtidos.
Análise e discussão de resultados
Considerando a participação de quinze docentes da área de Matemática e Música, a Figura 1 ilustra a distribuição de frequência desses professores com relação à primeira pergunta do questionário, tocante ao tempo de docência.
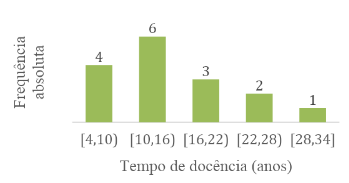
Figura 1: Histograma do tempo de docência
O segundo questionamento foi relativo ao conhecimento prévio sobre a teoria e/ou prática musical do respondente. Da amostra coletada, sete professores relataram já possuir algum conhecimento sobre o assunto, enquanto oito não o tinham, como ilustra a Figura 2. Interessante para a pesquisa o fato de ter-se uma distribuição praticamente equitativa para essa pergunta, pois há representatividade dos dois grupos: aqueles já familiarizados com a teoria e/ou prática da música e os que não o são.
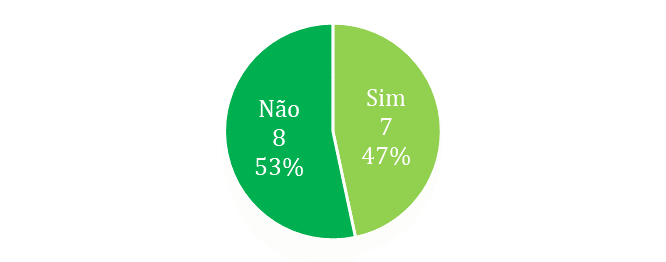
Figura 2: Conhecimento prévio de teoria e/ou prática musical
As demais questões, numeradas de 1 a 7 dizem respeito à apreciação das videoaulas. Em síntese, as perguntas dos itens 1 a 6, que envolvem a escala Likert(de 1 a 5), cujas respostas foram agrupadas na Figura 3, questionam: se a sintonia entre as duas linguagens já era evidente antes das videoaulas; se as videoaulas contribuem para a compreensão dessa conciliação; se as videoaulas contribuem para o entendimento dos conceitos; se a proposta deve compor a prática no Ensino Médio; se a lista avaliativa facilita a percepção da aplicação desses conceitos.
Quadro 2: Respostas dos Itens 1 a 6 para toda a amostra
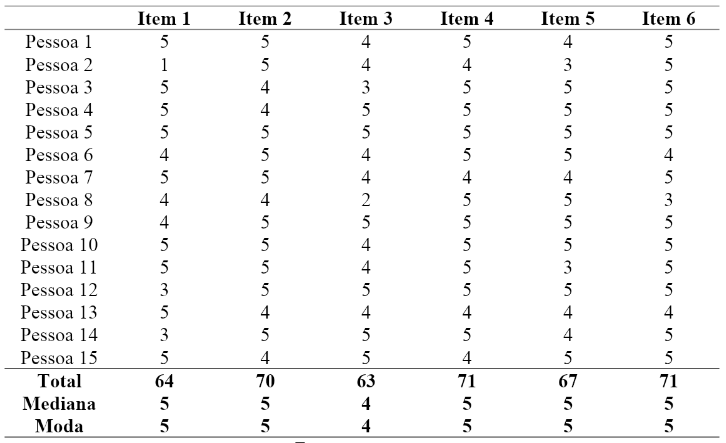
Uma análise foi obtida da comparação das respostas ao Item 1 - A sintonia entre Matemática e Música já era evidente antes de assistir às videoaulas separadas em extratos “sim” e “não” de acordo com a resposta à pergunta sobre conhecimento prévio de teoria e/ou prática. Foi executado o teste de Kruskal-Wallis entre os grupos, sendo obtido um p-valor de 0,24. Ou seja, não há diferença estatística entre o nível de concordância sobre a sintonia entre Matemática e Música para aqueles que já possuíam algum conhecimento musical e os que não possuíam tal conhecimento. Interpreta-se, então, que independente do conhecimento de Música, todos concordam igualmente com a sintonia dela com a Matemática.
Some-se a isso o fato que a Pessoa 2, que se manifestou nesse Item 1 discordando (nota 1) da evidência da relação entre Matemática e Música, e as Pessoas 12 e 14, que se mostraram indiferentes (nota 3), respectivamente, após assistir às videoaulas passaram a concordar totalmente (nota 5) em que essa conciliação contribuiu para a compreensão dessas duas linguagens, conforme resposta ao Item 2.
Ainda pode-se destacar que todas as modas e medianas, exceto do Item 3, foram classificadas como 5, ou seja, “concordo totalmente”, indicando grande aderência dos participantes à proposta de conciliação Matemática e Música. Esses altos valores de moda e mediana estão em acordo com as ideias de Gardner (1995): favorecer a construção de significados por meio do enlace dessas duas áreas, proporcionando maior diversidade de experiências.
O item 3, único com mediana e moda iguais a 4, indica um ponto de possível melhoria e que pode ser analisado juntamente com a resposta da Pessoa 8 ao Item Sugestões/Comentários: “Ensinar Matemática e Física através da Música implicaria partir do contexto concreto para apresentar a teoria. As aulas 2 e 3, por exemplo, trazem muita teoria e confesso que eu me dispersei. Me senti como os alunos numa aula em que eles não estão entendendo a matéria. Senti falta de imagens e sons para ilustrar a teoria”. Ou seja, a proposta poderia tratar conhecimentos musicais mais básicos para aqueles que não possuem familiaridade com essa temática.
Esta última afirmação da resposta da Pessoa 8 está em consonância com a opinião de outros participantes da pesquisa e merece destaque, como afirma, por exemplo, a Pessoa 3: "Essa abordagem excessivamente teórica é vista como antiquada em Educação Musical. Atualmente, valoriza-se mais a experiência como meio de construção do conhecimento musical. Igualmente, recusa-se definições estritas de “sons musicais”, como aparece no início da aula 4”; assim como aponta a Pessoa 4: “Gostei muito do projeto e das videoaulas, mas achei que faltou, principalmente na parte introdutória, sons que deixassem os exemplos mais palpáveis. Fiquei esperando tocar alguma daquelas partituras”.
Na mesma linha, há ainda o relato da Pessoa 10: “Sugeriria apenas que, nas videoaulas da parte relativa às partituras, que fosse mais detalhada e apresentasse sempre a imagem da relação entre as figuras para que, analfabetos musicais como eu possamos visualizar sempre as relações ‘fracionárias’”. De forma complementar, a Pessoa 13 indica uma possibilidade de se trabalhar mais a experimentação musical, conforme salienta: “Poderiam utilizar um marcador de tempo (metrônomo) para facilitar o entendimento das figuras musicais”.
Pitágoras e sua experiência com Música também foram citados pelos participantes. A Pessoa 13 indica: “Poderiam ter feito um vídeo reproduzindo a experiência de Pitágoras com o monocórdio.” A Pessoa 15, também nesse sentido, coloca: “Sugiro explorar melhor a ideia de Pitágoras: o uso de cordas de mesma espessura com comprimentos que são frações do comprimento de uma corda referência para montar uma escala musical”. De fato, esses questionamentos vão ao encontro do que afirmou Abdounur (2006): as descobertas de Pitágoras são um marco na relação entre Música e Matemática e consequentemente deveriam ser exploradas em um projeto que contemple o tema.
No tocante ao item 7, que questionava aos participantes: “No seu ponto de vista, qual(is) a(s) vantagem(ns) da conciliação entre Matemática e Música?”, e que permitia múltiplas marcações, obteve-se a distribuição de frequências apresentada na Figura 3.
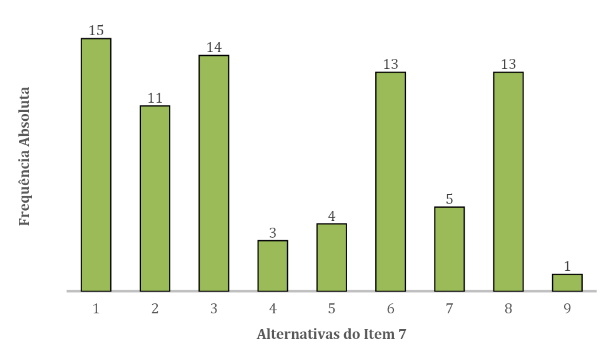
Figura 3: Distribuição de frequências para o Item 7
Merecem destaque positivo as afirmativas 1: “Evidencia que as ideias matemáticas estão presentes em situações reais da vida”, assinalada por 100% da amostra; 3: “Favorece a inovação da prática educativa”, assinalada por 93,3% da amostra; 6: “Torna o ensino da Matemática mais interessante”; e 8: “Revela mais uma aplicação para os conhecimentos matemáticos”, assinalada por 86,7% da amostra e 2: “Apresenta os conceitos matemáticos a partir de um contexto real”, assinalada por 73,3% da amostra. Todos esses itens estão na linha de construir uma matemática mais aplicada ao mundo real e ao conceito de um trabalho pedagógico inovador defendidas por Camargos (2010), ou seja, ensinar com alegria, aguçar o olhar curioso e estabelecer uma relação mais prazerosa com a Matemática, e Morais (2008), que afirma que a conciliação poderia ampliar o interesse e revelar mais uma aplicação para os conhecimentos matemáticos.
Atenção especial deve ser dada aos seguintes itens: 7: “Aproxima os conceitos matemáticos dos conhecimentos prévios do aluno”, assinalado por 33,3% da amostra; 5: “Diminui a abstração, tornando o conteúdo mais palpável”, assinalado por 26,7%; 4: “Ameniza o ‘medo’ da Matemática”, assinalado por 20%; e 9: “Desperta o interesse pela música em sua teoria e história”, assinalado por apenas 6,7% da amostra. Algumas reflexões importantes emergem da baixa adesão a esses itens: em especial o fato de que os conteúdos de teoria musical trabalhados podem não ser tão intuitivos, tampouco de baixa abstração, como acreditava-se antes da aplicação da pesquisa. Desse modo, uma adequação da profundidade dos temas trabalhados ao nível de conhecimento prévio dos discentes deve ser considerada em um projeto para conciliação dessas duas áreas. Essa afirmativa é corroborada pelas respostas de alguns dos participantes, como apresentado anteriormente.
Por fim, um importante questionamento foi realizado no Item Sugestões/Comentários pela Pessoa 7: “Considero importantes essas relações da Matemática com a música, porém, penso nos alunos que não apresentam tanta intimidade ou interesse pela música... O que fazer com estes outros alunos em um tipo de abordagem dessa?”.
Essa asserção nos leva a pensar qual o formato ideal para introduzir um projeto que relacione Música e Matemática na Escola Básica: trabalhar de forma extraclasse (ou em contraturno), pois não está no currículo formal de Matemática, ou discutir os conteúdos no período regular, com todos os alunos, justamente pela possibilidade de despertar naqueles resistentes o gosto pelas duas áreas quando apresentadas de forma conectada. Acredita-se que uma resposta a esse questionamento pode ser obtida aplicando-se efetivamente esse trabalho em sala de aula na Educação Básica e coletando resultados, algo que não foi trabalhado nesta pesquisa justamente por focar na validação entre pares. De certo modo, essa pergunta abre uma possibilidade para sequência desses estudos.
Considerações finais
Ao final da pesquisa, acredita-se que a conciliação entre Música e Matemática pode se apresentar como opção metodológica para aqueles que mostram certo encantamento com a Música, mas têm dificuldade com os conceitos matemáticos. Tanto a Matemática quanto a Música estão intimamente ligadas à vida de todas as pessoas. Porém, cada um, em sua própria história, em sua própria experiência, se relaciona com as duas de forma diferente.
Entende-se que a validação a priori, momento no qual os professores tiveram contato com as videoaulas, contribuiu de algum modo em seu processo formativo, ao propiciar a reflexão sobre as possibilidades dessa conciliação. Neste processo de validação, foi possível perceber que esta conciliação pode contribuir de forma significativa para a aprendizagem da Matemática, ao favorecer a inovação da prática educativa, tornar o ensino da Matemática mais interessante e revelar mais uma aplicação para os conhecimentos matemáticos, evidenciando-se assim que as ideias matemáticas estão presentes em situações reais da vida.
No entanto, devido a alguns fatores, tais como a abordagem conteudista mais teórica do que prática, alguns professores afirmaram talvez não se sentirem confortáveis em utilizar tal abordagem na sala de aula. Tais contribuições forneceram assim dados suficientes para avaliar, com base na perspectiva destes, os impactos das videoaulas para ampliação do conhecimento nos conteúdos acadêmicos.
Conclui-se então que, na perspectiva dos professores participantes, apesar de alguns pontos que merecem revisão, existe a possibilidade de conciliação entre Música e Matemática no processo de ensino de Matemática para o Ensino Médio. Pensando-se numa possível aplicação em sala de aula, seria interessante que as explicações fossem mais ilustrativas, tivessem exemplos de sons tocados ou cantados para prender a atenção do aluno e tornar mais fácil seu entendimento. Abre-se também a hipótese de esta conciliação ser expandida para além do Ensino Médio, ou seja, em cursos de graduação para futuros docentes.
Referências
ABDOUNUR, O. J. Matemática e música: pensamento analógico na construção de significados. São Paulo: Escrituras, 2006.
BONA, P. Método completo de divisão musical. São Paulo: Grafipress, 2004.
BRASIL. Ministério da Educação. Base nacional comum curricular. Brasília: MEC/SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 26 abr. 2020.
BRITO, Teca Alencar de Almeida. Música na Educação Infantil. São Paulo: Peirópolis, 2003.
CAMARGOS. C. B. R. Música e Matemática: a harmonia dos números revelada em uma estratégia de modelagem. Dissertação (Mestrado em Educação Matemática) – Universidade Federal de Ouro Preto, Ouro Preto, 2010. Disponível em: https://www.repositorio.ufop.br/handle/123456789/2497. Acesso em: 16 set. 2017.
D’AMBROSIO, U. A história da Matemática: questões historiográficas e políticas e reflexos na Educação Matemática. In: BICUDO, M. A. V. (Org.). Pesquisa em Educação Matemática: concepções & perspectivas. Rio Claro: Editora da Unesp, 1999.
______. A interface entre História e Matemática: uma visão histórico-pedagógica. In.: FOSSA, J. A. (Org.). Facetas do diamante. Rio Claro: SBHMat, 2000.
______. Educação Matemática: da teoria à prática. 2ª ed. Campinas: Papirus, 1997. Coleção Perspectivas em Educação Matemática.
FIORENTINI, Dario. A pesquisa e as práticas de formação de professores de Matemática em face das políticas públicas no Brasil. Bolema, Rio Claro, ano 21, nº 29, p. 43-70, 2008. Disponível em: https://www.redalyc.org/pdf/2912/291221870004.pdf. Acesso em: 16 abr. 2020.
FLEMMING, Diva Marília; LUZ, Elisa Flemming; MELLO, Ana Cláudia Collaço de. Tendências em Educação Matemática. 2ª ed. Palhoça: Unisul Virtual, 2005. Disponível em: http://paginapessoal.utfpr.edu.br/estephan/didatica-da-matematica/tendencias-em-educacao-matematica/tendencias%20em%20educacao%20apostila%20diva%20fleming.pdf/at_download/file. Acesso em: 07 abr. 2020.
FREIRE, P. Pedagogia da esperança: um encontro com a Pedagogia do Oprimido. Rio de Janeiro: Paz e Terra, 1997.
GARDNER, H. Inteligências múltiplas: a teoria na prática. Porto Alegre: Artes Médicas Sul, 1995.
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. 4ª ed. São Paulo: Atlas, 2002.
GIORDAN, Marcelo; GUIMARÃES, Yara A. F. Elementos para validação de sequências didáticas. Processos e materiais educativos na educação em Ciências. In: IX ENCONTRO NACIONAL DE PESQUISA EM EDUCAÇÃO EM CIÊNCIAS – IX ENPEC. Atas... Águas de Lindoia, 10 a 14 de novembro de 2013. Disponível em: http://www.nutes.ufrj.br/abrapec/ixenpec/atas/resumos/R1076-1.pdf. Acesso em: 16 abr. 2020.
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de Física: Gravitação, Ondas e Termodinâmica. v. 2, 10ª ed. Rio de Janeiro: LTC, 2016.
LINO, Dulcimarta Lemos. Música é... cantar, dançar... e brincar! Ah, tocar também. In: CUNHA, Susana Rangel Vieira da (Org.). Cor, som e movimento: a expressão plástica, musical e dramática no cotidiano da criança. 6ª ed. Porto Alegre: Mediação, 2006.
LORENZATO, S. O laboratório de ensino de Matemática na formação de professores. Campinas: Autores Associados, 2010. Coleção Formação de Professores.
MEDEIROS, C. F.Por uma Educação Matemática como intersubjetividade. In: BICUDO, M. A. V. Educação Matemática. São Paulo: Cortez, 1987.
MORAIS, Marcos Vinícius Gomes. Álgebra dos tons. Docplayer. Brasília: Universidade Católica de Brasília, Departamento de Matemática, 2008. Disponível em: https://docplayer.com.br/24203686-Algebra-dos-tons-marcos-vinicius-gomes-morais-universidade-catolica-de-brasilia-departamento-de-matematica-orientador-prof-sinval-braga-de-freitas.html. Acesso em: 29 mar. 2019.
PENNA, M. Reavaliações e buscas em musicalização. São Paulo: Loyola, 1990.
PIRES, C. M. C. Currículos de Matemática: da organização linear à ideia de rede. São Paulo: FTD, 2000.
RATTON, M. A relação harmoniosa entre sons e números. Programa 5: Música e Matemática. TV E Brasil, 2003. Disponível em: https://web.archive.org/web/20090502215418/http://www.tvebrasil.com.br/salto/cronograma2003/ame/ametxt5.htm. Acesso em: 07 abr. 2020.
Publicado em 28 de setembro de 2021
Como citar este artigo (ABNT)
VASCONCELOS, Andréia Miranda dos Santos; VASCONCELOS, Lucas da Silva; AMARAL, Sandra Regina do; DIAS, Tiago de Oliveira; ALMEIDA, Wálmisson Régis de. Matemática e Música no Ensino Médio: duas linguagens e uma sinfonia. Revista Educação Pública, v. 21, nº 36, 28 de setembro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/36/matematica-e-musica-no-ensino-medio-duas-linguagens-e-uma-sinfonia
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
1 Comentário sobre este artigo
Deixe seu comentário
Bom dia, prezados!
Fiquei muito feliz com este artigo. Gostaria de saber se têm mais material para que eu possa pesquisar.
Atenciosamente,
María Luiza Santos Cosme.
Este artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

