Uso de algeplacas no ensino da Matemática: explorando equações do 1º grau
Robson Silva de Paiva
Pós-graduando em Ensino de Ciências e Matemática (IFPB/UAB)
Roberta de Lourdes Silva dos Santos
Pós-graduanda em Ensino de Ciências e Matemática (IFPB/UAB)
Segundo o MEC (2016), a proposta da Base Nacional Comum Curricular (BNCC) de construção horizontal do conteúdo de Matemática para a Educação Básica contribui para solucionar um problema histórico da área: dando mais sentido ao mundo dos números no dia a dia dos alunos. Com o intuito de conhecer a realidade desses alunos e poder contribuir no seu aprendizado, escolhi para a temática de trabalho de conclusão do Curso de Especilização em Ensino de Ciências e Matemática, uso das algeplacas no ensino da Matemática.
O uso de algeplacas, quando bem elaborado, consegue trazer os alunos para uma realidade onde o ensino tradicional não os leva despertando o interessa pelo assunto. O professor tem o papel fundamental de estimular o aluno de maneira que ele desenvolva o seu próprio conhecimento, como é uma metodologia que vai aprimorar as habilidades, a capacidade de concentração e também vai desmistificar a mentalidade de que é complicado o estudar da Matemática no Ensino Médio.
Rêgo (2009) sugere que o professor: se entusiasme com a Matemática; personalize os problemas sempre que possível (usando nomes de personagens de historias, desenhos animados, ídolos da música ou da TV); reforce a perseverança, mais que a rapidez na resolução; encoraje os alunos a fazer estimativas; aceite e valorize métodos de resolução não usuais; enfatize o uso e seleção de estratégias de resolução e encoraje os estudantes antes na exposição de suas ideias e estratégias desolução.
É de grade importância que o professor seja facilitador do processo de manipulação, escolhendo uma forma adequada para que os alunos sejam descobridores do conhecimento onde o professor esteja presente e lhe auxiliando para que os mesmos sejam capazes de resolver as questões propostas de maneira prática e com seu próprio conhecimento já adquirido, sem se preocupar com o certo ou errado.
O uso das algeplcas para o ensino estimula os alunos a encontrar as estratégias de resoluções de problemas, assim eles estarão construindo seu próprio conhecimento diante do que foi proposto peloprofessor. Para uma melhor compreensão da pesquisa, o trabalho de investigação foi estruturado e subdivido em seis seções, da seguinte maneira: a primeira seção trata da “Introdução”, explanando sobre a justificativa da escolha temática, da problemática, dos objetivos e de uma breve ilustração acerca da estruturação do trabalho.
A segunda parte é constituida do “Referencial Teórico”, visando uma discussão teórica sobre o uso das “Algeplacas” no ensino da Matemática: Explorando Equações do 1ºGrau.
Na terceira seção, apresentamos a “Metodologia” adotada nesta pesquisa, relacionando os objetivos aos procedimentos para construção dos dados, enumerando separadamente a tipologia do estudo, os sujeitos da pesquisa e o universo e por fim, a aquisição e tratamento dos dados coletados e analisados.
Na quarta seção, apresentamos a “Análise dos dados”, a partir dos aspectos gerais do município de João Pessoa, característica da instituição observada, perfil do docente da instituição participante, perfil dos estudantes, situações Matemáticas, período de intervenção em sala de aula e sequência didática realizada na escola.
E ao término estão as “Considerações finais”, além das propostas para estudos futuros. Diante desta temática, convidamos o leitor a desvelar, juntos com os pesquisadores, as reais concepções evidenciadas pelos pesquisadores no ensino da Matemática a partir do uso das algeplacas apreciando a pesquisa atentando para as principais questões e anseios da comunidade educativa nas discussões que seguem.
Em função do exposto a pesquisa que orienta esse trabalho acadêmico visa faciltar a compreensão do ensino da Matemática atraves do uso das algeplacas. A pesquisa foi realizada em uma escola pública do munícipio de João Pessoa.
Elegemos como questão de pesquisa deste estudo o uso de algeplacas no ensino da Matemática: Explorando Equação do 1º Grau.
Desta forma, elencamos como objetivo geral analisar as contribuições metodológicas que o uso desse material concreto possibilita no ensino do conteúdo Equação do 1° Grau. Para respondermos ao objetivo geral deste estudo, elegemos os seguintes objetivos específicos:
- Levantar o perfil dos participantes com relação aos aspectos sociais,econômicos e cognitivos;
- Elaborar uma proposta didática que favoreça a compreensão conceitual de Equações de 1º grau;
- Aplicar proposta didática com o público participante.
Referencial teórico
Para um melhor entendimento da problemática de pesquisa, realizamos um estudo teórico sobre as principais questões que envolvem o uso de Metodologias no Ensino da Matemática na Educação Básica, com o intuito de entender a temática anunciada desenvolvemos um roteiro de estudo que se inicia discutindo e apresentando os dados referentes ao Ensino da Matemática no Ensino Médio. Por fim, apresentamos a sequência didática utilizada na escola observada.
Matemática no Ensino Médio
Conforme a pesquisa realizada pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Brasil, 2017), o Brasil conta com 184,1 mil escolas da Educação Básica, sendo que a maior parte (112,9 mil, o que equivale a dois terços) sendo de responsabilidade municipal. Deste total 21,7% são particulares. O ensino médio é oferecido em 28,5 mil instituições de ensino atendendo 7,9 milhões matriculados, dentre eles 7,9 % em atividades em tempo integral. Houve um aumento de 3,9 % considerando o período de 2013 a 2017.
No Brasil, a rede estadual é responsável pelo maior número de escolas de Ensino Médio. 68,2% delas pertencem a essa rede, seguidas da rede privada com 29,0% das escolas; 89,7% das escolas de Ensino Médio estão na zona urbana e 10,3% na zona rural – menor participação da zona rural em toda Educação Básica.
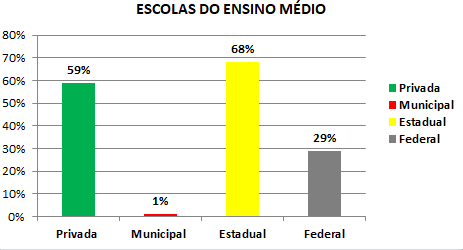
Figura 1: Administração das escolas de Ensino Médio
Fonte: Brasil (2017).
De acordo com as Diretrizes Curriculares para o Ensino Médio, deve-se considerar um amplo espectro de competências e habilidades a serem desenvolvidas no conjunto das disciplinas. O trabalho disciplinar pode e deve contribuir para esse desenvolvimento. Conforme destacam os Parâmetros Curriculares Nacionais para o Ensino Médio - PCNEM (Brasil, 2002) e os PCN+ (Brasil, 2002), indicam que o ensino da Matemática deve contribuir para que os alunos desenvolvam habilidades relacionadas à representação, compreensão, comunicação, investigação e, também, à contextualização sociocultural. A partir das competências e habilidades, o aluno desenvolve o pensamento matemático, não se restringindo apenas às resoluções de problemas, mas capacitando-o na forma de refletir sobre suas possibilidades, de compreensão lógica e de autonomia significativa e adequada.
A Matemática no Ensino Médio é de fundamental importância para estruturação do pensamento e do raciocínio dedutivo, desempenhando também o papel instrumental, considerando a Matemática uma ferramenta da vida cotidiana, contribuindo de maneira significativa para o desenvolvimento de atitudes, cuja utilidade e alcance transcendem o âmbito da própria Matemática.
O professor tem o papel fundamental no ensino e na aprendizagem do aluno, necessitando realizar pesquisas relacionadas à Matemática, bem como adotar metodologias de ensino para transmissão do conteúdo a ser estudado, capacitando o educando a resolver problemas genuínos, gerando hábitos de investigação, proporcionando confiança e desprendimento para analisar e enfrentar situações novas. O ensino da Matemática está baseado não apenas na teoria, livros e avaliações, mas também na prática pedagógica.
No Brasil, o ensino adequado teve aumento, considerando o Ensino Fundamental e o Ensino Médio, porém, existe um gargalo na disciplina de Matemática do terceiro ano do Ensino Médio, onde constatamos que, ao concluírem o Ensino Médio, apenas 7,3% dos estudantes atingem o nível satisfatório de aprendizado, sendo este o menor índice divulgado pelo Movimento Todos pela Educaçãodesde 2013, quando esse percentual era de 9,3%.
Matemática e o uso de metodologias de ensino
O uso de metodologias no ensino da Matemática é de fundamental importância para o aprendizado do aluno, porém, é de suma importância o domínio do conteúdo por parte do professor, uma vez que a escolha estratégica seja a mais adequada para o ensino em sala de aula.
Os Parâmetros Curriculares Nacionais (PCN) (Brasil, 1997; 1998), indicam a resolução de problemas como o fio “condutor” para se fazer Matemática em sala de aula durante toda Educação Básica. É importante destacar que o ensino a partir da resolução de problemas irá desenvolver a capacidade e raciocínio lógico do educando, tendo em vista que a metodologia de resolução de problemas, com uso de estratégias ou instrumentos de ensino ajudará também na aprendizagem de conceitos, procedimentos e atitudes.
Farias, Azeredo e Rêgo (2016) indicam algumas tendências metodológicas que hoje estão presentes em livros de Matemática para Educação Básica que serão tratados a seguir.
Segundo Polya (1995 apud Farias, Azeredo, Rêgo, 2016) a metodologia de resolução de problemas deve ser a principal metodologia de ensino da Matemática escolar. Esta deve seguir uma sequência de passos, denominada heurística, ajudando na compressão e resolução. São eles: (1) compreender; (2) elaborar um plano de ação; (3) executar o plano; (4) fazer uma verificação da pertinência da solução encontrada. O aluno, ao desenvolver a capacidade de resolver situações- problema matemáticas aumenta a sua autoconfiança, aprende a raciocinar passo a passo e efetuar uma análise de situações. Constrói conceitos de maneira significativa, e o que é mais importante, estará mais bem preparado para aplicar o conhecimento matemático em outros contextos.
A resolução de problemas pode ser apresentada em situações abertas que exijam dos alunos atitudes ativas, buscando novos conhecimentos. O ensino a partir de resolução de problemas pressupõe a construção de conhecimentos conceituais, atitudinais e procedimentais, assim como o conhecimento disponível adquirido.
A metodologia de jogos matemáticos, quando bem planejados e com objetivos claros, envolve diversos aspectos positivos, sendo possível identificar as dificuldades, sejam elas conceituais, procedimentais ou atitudinais do educando, a partir de contextos e situações que não são padrões diferentes do habitual.
Quando utilizado com recurso metodológico o jogo pode: motivar o aluno; introduzir conceitos de difícil compreensão; auxiliar do desenvolvimento de estratégias de resolução de problemas; capacitar o aluno a tomar decisões e saber avaliá-las. É importante destacar que o uso de jogo deve ser associado a outras metodologias, em especial a resolução de problemas, evitando assim o uso do jogo pelo jogo.
O ensino-aprendizagem de Matemática por meio da metodologia da resolução de problema e da utilização de jogos possibilita aos estudantes a criação de estratégia para resolução das situações problemas, a apropriação de conceitos matemáticos, “novas compreensões da Matemática embutida na tarefa” (Van do Walle, 2009, p. 58).
A Matemática e a Álgebra
A Álgebra é o ramo de conteúdo que estuda a manipulação de equações, operações Matemáticas, polinômios e estruturas algébricas. A Álgebra e um dos principais ramos da Matemática pura, juntamente com a geometria, tipologia, análise e teoria dosnúmeros.
A partir de uma análise dos PCN, o ensino de Álgebra está no tipo de pensamento e raciocínio, preparando o aluno a pensar matematicamente em todas as áreas da Matemática. O pensamento algébrico ou raciocínio algébrico envolve formar generalizações a partir de experiências com números e operações, formalizar essas ideias com uso de um sistema de símbolos significativo e explorar os conceitos de padrão de função, sendo o pensamento algébrico essencial para a vida cotidiana. O simbolismo, quando envolve equações e variareis, é usado para expressar generalizações aritméticas e estruturas do sistema numérico.
Para Van de Walle (2009, p. 288), a Álgebra envolve “generalizar e expressar essa generalização usando linguagens cada vez mais formais, onde a generalização se inicia na aritmética, em situações de modelagem, em geometria e virtualmente em toda Matemática que pode ou deve aparecer nas séries elementares”.
Algeplacas
O material didático denominado em português algeplacas e em inglês algeblocks tem inúmeras sugestões de atividades disponíveis em sítios de língua inglesa, especialmente. O material foi apresentado pela primeira vez em um encontro de Psicologia de Educação Matemática, em Lisboa, no ano de 1994, e suas peças envolvem o conceito de área de figuras planas simples, como quadrados e retângulos, estudados pelos alunos do Ensino Fundamental ainda nas séries iniciais deste nível de escolaridade. As experiências relatadas por professores que já fizeram uso do material em sala de aula apontam na direção de resultados bastante significativos, compreendidos por uma melhor compreensão das operações algébricas, às quais os alunos passam a atribuir significado, uma vez que as ações realizadas com o material, e a reflexão sobre elas, possibilitam a construção de modelos mentais sobre os quais o aluno poderá realizar generalizações e formalizações.
Quando isso não acontece, o professor se vê obrigado a repetir ou rever constantemente conteúdos já estudados, pois o que prevaleceu à época de seu estudo compreendeu apenas o uso da memorização de regras. Além disso, conteúdos como Fatoração de polinômios ficam mais fáceis de serem posteriormente trabalhados com os alunos.
O que inicialmente parece tomar tempo, uma vez que a execução de atividades com materiais manipulativos requer um ritmo de ação muito mais elaborado por parte do professor e da turma, do que demanda uma aula tradicional - onde o professor cópia informações no quadro, as lê para a turma e explica um conjunto de exercícios do tipo padrão-, mas compreenderá um investimento na qualidade do que se faz em termos de ensino e de aprendizagem em curto, médio e longo prazos.

Figura 2: Apresentação de materiais concretos no ensino da equação do 1ºgrau

Figura 3: Atividade em sala com as algeplacas
Metodologia
Material utilizado: Cartolinas de duas cores. O material é recortado de forma a obter quadrados e retângulos de tamanhos distintos.
Procedimento: Inicia-se solicitando aos alunos que identifiquem a área de cada figura, em função das medidas dos lados dos retângulos, indicados por números ou letras, para que possam realizar os procedimentos de codificação e decodificação algébrica com base nas placas. Se o quadrado tem lados com medidas iguais a x unidades de comprimento, sua área será igual a x2 unidades quadradas; se tem lados iguais a y unidades de comprimento, o quadrado terá y2 unidades de área; se os lados do quadrado são iguais a uma unidade de comprimento, sua área será 1 unidade quadrada; se a figura é um retângulo e seus lados são iguais a x e y unidades de comprimento, sua área será dada por x.y unidades quadradas. É importante lembrar aos alunos que, embora nas expressões sejam indicados apenas elementos como x, x2 ou y, estes indicam os valores de áreas e que na representação tiveram as unidades suprimidas. Uma vez preparado o material (quadrados e retângulos de cartolina), propor situações que visam responder às questões: dado um conjunto qualquer de peças, como representar algebricamente os seus elementos? E dada a representação algébrica de um conjunto de peças, qual o material concreto correspondente, ou seja, quais as peças que serviram de base para a representação algébrica? Inúmeras expressões podem ser apresentadas aos alunos, como: 4x2 + 2y + 1; 2xy + 3y; – x2 + 4; 3y2 + 8x - 6; y2 - xy, entre outras. Após fazer diversas ações de codificação, o professor deverá trabalhar com os casos de cancelamento de áreas, que se dá através da junção de peças iguais em tamanho e forma, porém de cores diferentes. É importante destacar que não se está trabalhando com áreas negativas (o que não existe), mas que se está somando ou subtraindo o valor correspondente às áreas das figuras, dependendo de sua cor.
A metodologia desenvolvida neste estudo foi de abordagem exploratória do tipo pesquisa quanto aos objetivos, do tipo estudo qualitativa na aquisição e análise dedados.
O estudo foi exploratório, definido por Gil como tendo como “principal finalidade esclarecer e modificar conceitos e ideias, tendo em vista a formulação de problemas mais precisos ou hipóteses pesquisáveis para estudos posteriores” (Gil, 2011, p. 27). Estudos dessa natureza podem envolver levantamento bibliográfico e documental, entrevistas não padronizadas e estudo de caso, segundo o autor.
Quanto ao levantamento e análise de dados, esta pesquisa se caracteriza como sendo um estudo qualitativo. Segundo Gil (2011), é um método abrangente que permite chegar a generalizações amplas e que facilitam a compreensão da realidade. A pesquisa se desenvolveu no espaço da sala de aula, em uma turma do 1º ano do Ensino Médio no turno da noite na Escola Cidadã Integral de Ensino Fundamental e Médio Professora Daura Santiago Rangel, localizada no município de João Pessoa/PB, com 32 estudantes participantes, com aplicação de tarefas diversificadas ao longo do mês de maio do corrente ano.
A partir do estudo metodológico, utilizamos de dois instrumentos de pesquisa para obtenção dos dados: questionários Pré-teste e Pós-teste semiestruturados abrangendo o perfil dos estudantes do 1º ano A, no que se refere aos aspectos sociais, econômicos e cognitivos, e perfil do professor, a fim de buscar informação sobre as atividades desenvolvidas e perfil da escolaestudada.
Para atingir os objetivos da pesquisa, optamos por realizar cinco intervenções em sala de aula com 45 minutos cada uma, além de realizar duas observações na escola investigada. A pesquisa iniciou no mês de abril com as observações e se encerrou no mês de maio com as intervenções. O questionário utilizado abordou o perfil socioeconômico e cultural dos estudantes e professor. O questionário aplicado com os estudantes, além de terem questões envolvendo o perfil dos mesmos, constavam quatro questões (pré-teste) envolvendo o conteúdo de equação do 1º grau, a fim de analisar o nível de conhecimento dos estudantes. Sendo assim, este trabalho foi dividido em cinco momentos. Veja no Quadro 2 o que foi desenvolvido na Escola Cidadã Integral de Ensino Fundamental e Médio Professora Daura Santiago Rangel.
Quadro 1: Cronograma de atividades realizadas na escola
Período |
Tarefas desenvolvidas |
Março/2018 |
Visita à escola |
Abril/2018 |
Aplicação de questionários (pré–teste) para avaliar o perfil dos estudos e do professor |
Abril/2018 |
Observação em sala de aula |
Maio/2018 |
Desenvolvimento das atividades abrangendo equação do 1º grau durante as intervenções |
Maio/2018 |
Aplicação do questionário (pós-teste) com os estudantes |
Iniciamos a pesquisa com uma visita à escola, quando entrevistamos a vice-diretora, sempre muito atenciosa e disposta a ajudar com as informações necessárias para atividade a ser desenvolvida. Após entrevista, fomos para a sala de aula, onde fomos bem recebidos pelos alunos e professor responsável, realizamos o pré-teste com objetivo de avaliar e conhecer os estudantes participantes, e então traçarmos as atividades a serem aplicadas. Para auxiliar nas exemplificações dos conceitos trabalhados, utilizamos o material concreto e manipulativo, as algeplcas confeccionadas em EVA.
Participaram da pesquisa todos os estudantes do 1° ano A da escola, localizada na zona urbana do município de João Pessoa/PB. Constatamos que 64% dos estudantes têm a faixa etária entre 15 a 17 anos, 30% entre 17 a 19 anos e 7 % dos estudantes tem a idade maior de 19 anos, estando estes no quadro dos estudantes em situação da distorção idade-ano, proporção de alunos com mais de 2 anos de atraso escolar. A turma do 1° ano A do Ensino Médio da Escola Professora Daura Santiago Rangel é composta por dezenove estudantes do sexo feminino, o que corresponde a 59% dos estudantes, e treze estudantes do sexo masculino, o que corresponde a 41% dos estudantes.
Deles, 70% moram próximo à escola, sendo possível vir a pé; e 30% moram distante, havendo necessidade de um meio de transporte. A maioria respondeu que mora com os pais e uma pequena parte mora na sua própria residência.
Quanto questionados sobre o interesse pela Matemática, identificamos que 46% dos estudantes gostam, porém sentem dificuldades e 54% não gostam, acham complicado e de difícil compressão. A pesquisa foi realizada com os alunos do turno da noite, onde constatamos que 45,83% trabalham e que 54,16% nunca trabalharam. Perguntamos se gostavam de estudar nesse horário 87,5% gostam e 12,5% não gostam, porém, alguns estudantes trabalham durante o dia e outra parte estuda por opção. Referente à ajuda nas tarefas escolares, 41,6% recebe ajuda dos familiares e 58,3% não recebem ajuda; isso nos ajuda a compreender a dificuldade que a maioria tem em sala de aula por falta de incentivo dos seus familiares. Sobre a vida escolar dos pais, pode-se observar que a maioria é de baixa escolaridade. Ficou assim o resultado: Ensino Fundamental, 83,3%; Médio 12,5%; não estudou, 4,1%.
Resultados e discussão
A verificação final dos resultados foi realizada a partir de um questionário composto por quatro questões abertas, envolvendo o conceito de equação e resolução de situações problemas. O intuito foi de verificarmos o nível de assimilação dos alunos com relação à temática investigada. Os resultados foram satisfatórios e estão apresentados de forma sintetizada, na Tabela 1.
Tabela 1: Síntese dos resultados do pós-teste
Questões |
Acertos |
Erros |
Não participante do pós-teste |
Questão 1 |
63% |
12% |
25% |
Questão 2 |
59% |
16% |
25% |
Questão 3 |
51% |
24% |
25% |
Questão 4 |
48% |
27% |
25% |
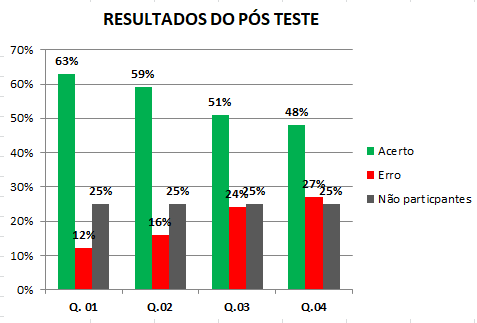
Figura 4: Síntese dos resultados do pós-teste
A Figura 4 representa o gráfico da síntese dos resultados do pós-teste, valores correspondentes ao percentual de acertos e erros por questões, bem como o percentual dos alunos não participantes da atividade.
Apresentamos de forma aleatória os registros das resoluções da Questão 1 desenvolvida pelos estudantes no pós-teste, considerando os acertos e erros comuns praticados.
Durante o período de intervenção realizamos diversas atividades com intuito de o aluno compreender o conteúdo de forma satisfatória a resolver questões relacionadas à equação do 1º grau, seja, a resolução de um cálculo ou situações problemas. Utilizamos como metodologia de ensino o uso de algebrplacas, esses materiais são caracterizados pelo envolvimento físico dos alunos em uma situação de aprendizagem ativa e reflexiva e se diferenciam dos materiais de dados estatísticos que só se prestam a observação.
Verificamos que o resultado final foi satisfatório com relação ao pré-teste, pois percebemos que houve evolução dos estudantes em relação à assimilação do conteúdo. O controle de atenção dos participantes também foi mobilizado com êxito, assim como a compreensão dos problemas propostos. Concluímos que a adoção de uma metodologia não tradicional desenvolvida em sala de aula, contribui significativamente para o entendimento e aprendizado do aluno.
Considerações finais
O presente trabalho de conclusão de curso espera proporcionar ao aluno da disciplina de Matemática uma melhor compreensão do conhecimento matemático e que o professor possa tornar eficaz o processo de ensino-aprendizagem. Para que esse processo aconteça à proposta aqui apresentada é que o professor utilize de metodologias não tradicionais, onde haja a participação do aluno e a reflexão do temaproposto. Para que o aluno não generalize o ensino da Matemática como difícil de aprender, o papel do professor é descobrir essa visão. Ao realizar a atividade em sala de aula, tive a oportunidade de vivenciar as dificuldades encontradas pelo professor, além de ensinar, enfrentar as barreiras do dia a dia, onde alguns alunos não têm o menor interesse em aprender mesmo diante de uma aula bem elaborada e com um didática diferenciada; é imporante e priomordial que o governo invista em incentivos para que os alunos não abandonem os estudos, pois esse comportamento reflete na desigualdade social.
Referências
BRASIL. Lei de Diretrizes e Bases da Educação Nacional, n° 9.394/96. Disponível em: http://portal.mec.gov.br/docman/julho-2013-pdf/13677-diretrizes-educacao-basica-2013-pdf/file. Acesso em:18 maio 2018.
______. Ministério da Educação, Secretaria de Ensino Médio. Parâmetros Curriculares Nacionais. Ensino Médio. Brasília: MEC/SEM, 2000.
______. Base Nacional Comum Curricular. Brasília: MEC/SEB, 2016. Disponível em: http://portal.mec.gov.br/pdf/bncc.pdf. Acesso em:11 abr. 2018.
FARIAS, Severina Andréa Dantas de; AZEREDO, Maria Alves de; RÊGO, Rogéria Gaudêncio do. A Matemática no Ensino Fundamental: considerações teóricas e metodológicas. João Pessoa: Editora Universitária da UFPB, 2016.
GIL, A. C. Métodos e técnicas de pesquisa social. 6ª ed. São Paulo: Atlas, 2011.
PASSOS, C. L. B. Materiais manipuláveis como recursos didáticos na formação de professores de Matemática. In: LORENZATO, S. (Org.). O laboratório de ensino de Matemática na formação de professores. São Paulo: Autores Associados, 2006.
POLYA, G. A arte de resolver problemas. 2ª ed. São Paulo: Hermann, 1995.
RÊGO, R. G. Tópicos Especiais em Matemática III. In: ASSIS, J. G. et al. Licenciatura em Matemática a distância. Vol. 6. João Pessoa: Editora Universitária da UFPB, 2009.
VAN DE WALLE, J. A. Matemática no Ensino Fundamental: formação de professores e aplicação em sala de aula. Trad. Paulo Henrique Colonese. 6ª ed. Porto Alegre: Artmed, 2009.
Apêndice
Questionário aplicado com os estudantes juntamente com o pré-teste
Estamos realizando este questionário com o intuito de identificar algumas características que acompanham os estudantes ao concluírem o Ensino Médio nas escolas do município de João Pessoa/PB.
Gostaríamos de contar com a sua participação voluntária, sabendo-se que a qualquer momento você poderá interromper suas respostas sem que haja qualquer dano a você ou a esta instituição de ensino. Os dados desta pesquisa serão utilizados na elaboração de um trabalho de conclusão de curso e poderão ser publicados em revistas científicas.
Caso haja qualquer dúvida na sua participação ou nas perguntas deste questionário, favor dirigir-se ao pesquisador. Nas questões de múltipla escolha você poderá ter mais de uma alternativa como resposta.
1. Qual a sua idade? a.( ) entre 15 a 17 anos b. ( ) entre 17 a 19 anos c. ( ) maior que 19 anos
2. Qual seu sexo? a.( ) Feminino b.( ) Masculino
3. Você mora perto da escola? a.( ) sim b.( ) não
4. Você mora com seus pais? a.( ) sim b.( ) não
5. Você gosta de Matemática? a.( ) sim b.( ) não Por quê?
6. Você gosta de estudar no horário da noite? a.( ) sim b.( )não
7. Você recebe alguma ajuda para resolver as tarefas escolares de Matemática? a.( ) sim b.( ) não
8. Em que tipo de escola você cursou o ensino fundamental?
9. Com quantos anos você conclui o ensino fundamental?
10. Até que série seu pai estudou? a. ( ) Fundamental b. ( ) Médio c.( ) Superior d.() Não estudou
11.Até que série sua mãe estudou? a. ( ) Fundamental b. ( ) Médio c.( ) Superior d.( ) Não estudou
12. Você trabalha, ou já trabalhou, ganhando algum salário ou rendimento? a.( )sim b.( )não
13. A renda total de sua família fica em torno de:
Situações de Matemática
- Escreva a equação do 1° grau na forma geral: 3x + 8 = x+2
- Resolva a equação do 1º grau: 3x + 4 = 2x +6
- O dobro de um número, diminuído de 4, é igual a esse número aumentado de 1. Qual é esse número?
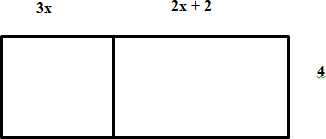
- Calcule a área de um retângulo cujo lado mede 3x e 2x +2 e a altura mede 4.
Publicado em 19 de outubro de 2021
Como citar este artigo (ABNT)
PAIVA, Robson Silva de; SANTOS, Roberta de Lourdes Silva dos. Uso de algeplacas no ensino da Matemática: explorando equações do 1º grau. Revista Educação Pública, v. 21, nº 38, 19 de outubro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/38/uso-de-algeplacas-no-ensino-da-matematica-explorando-equacoes-do-1-grau
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

