A concepção da Matemática através da história
Taciana Rodrigues Pombo
Licenciada em Matemática (UFOP)
Claudiney Nunes de Lima
Orientador do CEAD/UFOP e professor da Universidade Federal de São João del Rei /UFSJ – MG
A história da Matemática aduz os primeiros registros de pensamentos matemáticos que marcaram o desenvolvimento dessa ciência no início da Pré-História. Com o surgimento das primeiras deduções lógicas, decorrentes das necessidades práticas de sobrevivência, como aponta Silva (2014), sobrepostas em teorias, expressões e fórmulas utilizadas no cotidiano, a Matemática e as civilizações evoluíram praticamente na mesma proporção.
Compreendida como ciência do raciocínio lógico e abstrato, a Matemática apresenta várias linhas de estudos e, em suas particularidades, a magnitude existente em cada uma delas. Considerando as diversas tendências educacionais e a busca pela melhoria de ensino e da aprendizagem da Matemática, o presente trabalho busca investigar de que forma a Matemática historicamente contada pode contribuir para o processo de ensino-aprendizagem agregada com outros recursos que possam motivar o interesse dos alunos pela disciplina e amenizar a dificuldade no aprendizado. Nesse sentido, Chaquiam (2017, p. 14) ressalta que, diante de algumas pesquisas, alguns autores acreditam que o uso da História da Matemática contribui para o desenvolvimento cognitivo do aluno, pois
a história da Matemática, combinada com outros recursos didáticos e metodológicos, pode contribuir para a melhoria do ensino e da aprendizagem da Matemática, emerge como uma possibilidade de buscar uma nova forma de ver e entender a Matemática, tornando-a mais contextualizada, mais integrada às outras disciplinas, mais agradável, mais criativa, mais humanizada (Chaquiam, 2017, p. 14).
Entretanto, o papel do educador como agente transmissor de conhecimento reflete sua importância no processo de ensino-aprendizagem no qual a tipologia metodológica utilizada atua como ferramenta principal. Ademais, percebemos que esse processo está além do ensino mecânico, tomado por repetição e memorização, visto que professor e aluno podem caminhar juntos, porque,
se o educador articula o conhecimento matemático como coadjuvante da libertação do aluno como agente social, saberá que este terá de dominar com competência, e não sem esforço, aqueles conteúdos matemáticos que serão úteis para uma melhor atuação na sociedade (Piovesan et al., 2008, p. 3).
Sendo assim, é possível perceber que, para evitar que a aplicação da Matemática se desvie do seu sentido real, é recomendável envolver na metodologia de ensino mecanismos que deem significados ao estudo dessa disciplina, compreendendo que a Matemática não é apenas uma simples ferramenta inventada para compreender o mundo natural, pois ela é de fato verdadeira, real, e está presente em todo lugar.
Aprender Matemática é mais do que manejar fórmulas, saber fazer contas ou marcar x nas respostas: é interpretar, criar significados, construir seus próprios instrumentos para resolver problemas, estar preparado para perceber esses mesmos problemas, desenvolver o raciocínio lógico, a capacidade de conceber, projetar e transcender o imediatamente sensível (Paraná, 1990, p. 66 apudPIOVESAN et al., 2008).
Irene de Albuquerque (s.d), referenciada por Kashiwakura et al. (2013), destaca as frases que revolucionaram o ensino da Matemática, “um bom ensino da Matemática forma melhores hábitos de pensamento e habilita o indivíduo a usar melhor sua inteligência”, enfatizando que a metodologia de ensino faz uma grande diferença.
Todavia, a aprendizagem da Matemática necessita de procedimentos que possibilitem ao aluno a concessão do saber matemático estabelecendo sentido e significado, criar estratégias e construir novos caminhos. Diante disso, o que se procura investigar aqui é: quais são as possíveis causas que levam à dificuldade de aprendizagem e à rejeição da disciplina de Matemática, bem como os métodos que estão sendo utilizados para sanar esse problema?
Em busca de uma possível resposta, foi produzido este trabalho científico de cunho dissertativo, observando argumentações em outros materiais já publicados, como artigos, dissertações e monografias, entre outros, defendendo pontos de vista comuns entre eles correlacionados ao tema aqui presente. Logo, os parâmetros deste trabalho se dão por meio de revisão bibliográfica, cuja metodologia engloba estudo, leitura e pesquisa em outros materiais mencionados anteriormente.
Partindo da introdução, o trabalho é estruturado por capítulos e discussões que definem a importância de utilizar a História da Matemática na metodologia de ensino embasando a origem da Matemática e sua trajetória ao longo dos tempos, enfatizando também as relações dos símbolos, fórmulas e outras linguagens matemáticas presentes no cotidiano. Em sequência, a prática de ensino caracteriza fases de tendências educacionais que julgam as relações entre professor e aluno dentro da sala de aula. Por fim, os resultados e discussões apresentados no trabalho contribuem para o objetivo geral da pesquisa, no qual adotar procedimentos metodológicos criando estratégias que auxiliam na concepção da Matemática possibilita ao aluno a concessão do saber matemático com mais praticidade. Cabe ressaltar que as ideias extraídas de outros trabalhos científicos foram fundamentais para elaborar este estudo e, buscando referenciar esses autores que trabalham à luz do tema, será construído um referencial teórico que trará conceitos e concepções apresentados a seguir.
Um breve histórico do desenvolvimento da Matemática: os primórdios, a escrita e o sistema de numeração
“Os números governam o mundo”
Pitágoras, 585-495 a.C.
Acreditamos que os primeiros vestígios da Matemática iniciaram com os povos primitivos ainda nos tempos da caverna. Rossetto (2013) frisa que ainda no início da Idade da Pedra as principais atividades dos primatas eram a caça e pesca, extraindo da natureza todos os meios para manter a sobrevivência. De acordo com Miyaschita (2002), o processo de contagem surge antes mesmo da escrita, na percepção entre semelhanças e desigualdade, pois
a percepção de quantidade pelo homem primitivo era praticamente intuitiva, como a dos animais. A contagem para o homem era: um, dois e muitos, ou seja, a partir de um grupo de três ou quatro objetos o homem dizia simplesmente que havia muitos objetos nesse grupo (Miyaschita, 2002, p. 5).
Além disso, Miyaschita (2002) afirma que a ideia de diferenciar “muitos ou poucos” acontece ainda na Idade da Pedra, através da caça; mais tarde, os primatas acabam se tornando nômades, por deixarem suas cavernas em busca de outros lugares que lhes proporcionassem mais recursos alimentícios, entendendo ainda que o homem passa a construir sua própria civilização, cultivar seu próprio alimento e se dedicar à criação de animais. Segundo confirmam especialistas, os primeiros indícios do processo de contagem são encontrados em marcações em ossos e bastões de madeiras, além da utilização de partes do corpo como dedo das mãos e pés. Essa síntese pode ser confirmada por Mol (2013), ao dizer que
partes do corpo, como os dedos das mãos ou dos pés, funcionaram como instrumentos de contagem naturais. Pedregulhos, conchas ou grãos, bem como marcas no chão, na areia, em ossos ou madeira, poderiam ser empregados para quantificar o número de pessoas em uma população, de animais em um rebanho ou ainda o número de dias decorridos de determinado evento (MOL, 2013, p. 13).
No entanto, o crescimento das civilizações e a permanência nos locais acarretaram a produção de mais alimentos e, diante da necessidade de controlar os bens comerciais, surgiu a escrita, marcando o fim da Pré-História e o início da História. Posteriormente aos primeiros vestígios de pensamentos matemáticos advindo das culturas primitivas, a Matemática evoluiu no Egito e na Mesopotâmia.
A necessidade de registrar determinados objetos simbolicamente de maneira unificada e organizada em grupos pressupõe, de acordo com algumas descobertas arqueológicas, que o desenvolvimento da escrita aconteceu após o processo de contagem. Desse modo, transformar os resquícios de contagem grafadas em materiais primários e correspondê-los numericamente foi um grande avanço para a humanidade, dando início a um novo sistema de numeração.
O sistema de numeração, como trata Mol (2013), foi desenvolvido na Mesopotâmia, assumindo modelos numéricos por meio de símbolos e se aperfeiçoando em outras regiões. Entretanto, Miyaschita (2002, p. 5) afirma que “os primeiros registros de escrita numérica são os dos egípcios e os dos sumérios, surgidos por volta de 3500 a.C.”. Paralelo ao sistema de numeração, Mol (2013) defende que as necessidades práticas da civilização egípcia serviram de estímulo para o desenvolvimento da Matemática. Silva (2014) assume que os grandes progressos que marcaram o fim da Pré-História se pronunciaram com bastante intensidade e rapidez no Egito, porque os egípcios, além de adotar um modelo de sistema de numeração de base 10 não posicional, em que diferentes símbolos representavam 1, 10, 100 etc. e que cada símbolo poderia repetir por diversas vezes, como trata Mol (2013), registros encontrados em papiros, documento da época, mostram que os egípcios também tinham grande domínio nos cálculos geométricos. Os papiros de Rhind, os mais célebres, contêm 84 problemas de Geometria e Aritmética, seguidos de resoluções. Já o papiro de Moscou era composto por 25 problemas envolvendo cálculos de volume de pirâmides de base quadrada.
Os romanos, segundo Silva (2014), adotaram as letras I, V, X, L, C, D, M (1, 5, 10, 50, 100, 500 e 1000) para especificar os números, em que apenas os algarismos I, X e C podem repetir até três vezes e quando são colocados à esquerda de outro algarismo maior efetuam como subtração. Geralmente os algarismos romanos também são utilizados para indicar séculos, capítulos de livros, horas, nomes etc.
Miyaschita (2002, p. 30) salienta que “os gregos utilizavam um sistema de numeração semelhante ao sistema romano, valendo-se de letras de seu alfabeto para representar os números”, formando números a partir de uma série de símbolos gregos agrupados. Ademais, as letras do alfabeto grego também servem para denotar símbolos matemáticos que utilizamos atualmente.
Por fim, entre diversos modelos numéricos adotados pelos povos antigos, contamos com o mais célebre sistema de numeração, que revolucionou a escrita numérica, o indo-arábico, composto por dez algarismos representando os números 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, podendo a partir deles representar qualquer quantidade numérica; é o mais popular e mundialmente conhecido.
Teoricamente, compreendemos que o sistema de numeração foi a primeira transformação matemática devido às necessidades humanas, partindo do concreto para o abstrato. Com o surgimento dos números, a partir do processo de contagem, foi possível realizar operações elementares entre eles, compreendendo um universo chamado Aritmética. Por um processo abstrato, a Aritmética destacava em um dos quatros campos de estudo da escola pitagórica. Logo, Pitágoras, em sua filosofia, conjura os números como entidade mística e objeto de devoção.
De acordo com Mol (2013), os pitagóricos compreendiam o universo por meio da Aritmética implicando que “todas as coisas são números”. E a partir da introdução dos números foi possível florescer outros campos de estudos relacionados à Matemática. Ademais, não obstante o desenvolvimento da escrita numérica simbólica, acredita-se ainda que as atividades práticas e comerciais foram pioneiras para representar os números em forma de conjuntos. Analogamente a essa ideia, foram desenvolvidos os conjuntos numéricos, especificando a utilidade e a característica de cada um, que serão apresentadas no tópico a seguir.
Agrupamento dos números
A maneira com que o homem passou a enxergar o mundo deu origem a grandes descobertas, principalmente na área da Matemática. Após atribuir valores numéricos aos símbolos para quantificar determinados elementos, surgiu a ideia de agrupá-los em conjuntos, de acordo com sua utilização e suas características. Posteriormente ao processo de contagem e ao sistema indo-arábico, a partir dos dez algarismos (0, 1, 2, 3, 4, 5, 6, 7, 8 e 9), surgiu o conjunto dos números naturais, representado pela letra N, envolvendo um conjunto infinito de números inteiros positivos, utilizados no processo de contagem. Entretanto, o crescimento do comércio levou o homem a realizar cálculos em que os sinais operatórios de soma (+) e subtração (-) indicavam situações de ganho e perda. Com isso, denotamos o conjunto dos números inteiros, representados pela letra Z, abrangendo os números naturais inteiros positivos e negativos. Tendo em vista que as adversidades cotidianas levaram ao desenvolvimento da Matemática, foi a partir do sistema de repartição adotado pelos egípcios que se desenvolveram as frações. Segundo Mol (2013), a sociedade egípcia se desenvolveu próximo ao vale do Rio Nilo. Todavia, em uma das estações do ano um fenômeno natural fazia o Rio Nilo transbordar, o que mais tarde desmarcava as terras que foram distribuídas pelo rei. De acordo com Gayo (2012), como os impostos eram pagos conforme o tamanho da propriedade, era fundamental que os escribas, funcionários do rei, tivessem conhecimento sobre frações. Para Barasuol (2006, p. 3), “a Matemática egípcia é conhecida pelas suas frações unitárias, que eram necessárias quando os salários eram pagos com pão e cerveja”. Essa síntese mostra que os egípcios realizavam cálculos com frações em diversas atividades. Partindo da necessidade de representar divisões não exatas, obtém-se o conjunto números racionais, representados pela letra Q. Esse conjunto, segundo Gayo (2012), assume em sua representatividade os números decimais, os números inteiros e naturais resultantes de divisões exatas ou não.
Ainda partindo da ideia de medir, foi pelo estudo da Geometria desenvolvida pelos pitagóricos que se descobriram os números irracionais. Segundo Gayo (2012, p. 68), “apesar de os egípcios conhecerem a raiz quadrada há muito tempo, eles acreditavam que a raiz quadrada se tratava de um caso especial de fração”. Entretanto, foi com a aplicação do Teorema de Pitágoras ao calcular os catetos de um triângulo retângulo de lados iguais a 1, que os pitagóricos encontraram como √2 o valor da hipotenusa, constatando então que esse valor se tratava de dízimas não periódicas e que ainda não poderiam ser escritas como frações. Analogamente, Mol (2013) descreve que
o número hoje conhecido por √2 pode ter sido obtido de duas formas distintas. De uma maneira geométrica, ao se calcular a diagonal do quadrado de lado 1. Ou ainda, de uma forma puramente aritmética, obtendo-se a média geométrica entre a unidade e duas vezes a unidade, ou seja, 1/x = x/2 (Mol, 2013, p. 34).
Contudo, apuramos que, partindo do estudo das raízes, surgiram os números irracionais, dando existência ao novo conjunto, representado pela letra I, que, por ser incomensurável, abrange soluções não exatas, como dízimas não periódicas e raízes não exatas, não podendo ser representadas por meio de frações. Ademais, partindo da necessidade de organizar os números em um único conjunto, formamos o conjunto dos números reais, representado pela letra R. Entretanto, com todos esses números era impossível solucionar raízes de equações polinomiais simples, como x²+1=0, mas após inúmeras tentativas de solucionar problemas com raízes negativas, também chamado de números fictícios, nasceu a ideia de operar a partir de um número imaginário 𝒊 que se baseia na raiz quadrada de (−1), surgindo então o conjunto dos números complexos, representado pela letra C. Portanto, a representatividade da união desses conjuntos pode ser expressa conforme apresentado na Figura 1.
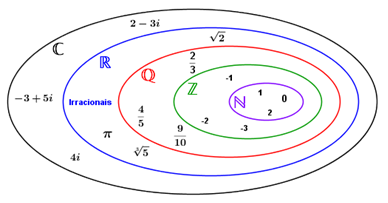
Figura 1: Representação gráfica dos conjuntos numéricos
Fonte: Central exatas.com. Acesso em: 22 abr. 2021.
Existe uma especulação de que os primeiros indícios dos pensamentos matemáticos, assim como sua evolução, provêm das necessidades práticas cotidianas. Com a revisão bibliográfica de alguns trabalhos científicos, apresentamos de maneira resumida a origem da Matemática e de seus conceitos numéricos. Dando continuidade ao trabalho, será mostrado no tópico a seguir o desenvolvimento da Matemática e suas contribuições.
A contribuição da Matemática para o desenvolvimento da humanidade
Resquícios deixados pelas civilizações primárias mostraram, segundo registros históricos, os primeiros indícios da evolução da Matemática a partir de deduções e pensamentos lógicos, nos quais a maneira com que o homem passou a enxergar o mundo deu origem a grandes descobertas. Consideradas por Boyer (2012) como ciência dos números, grandezas e formas, as atividades matemáticas advindas da consciência humana refletem na Aritmética, contagem e modelos geométricos. Ainda na Antiguidade, em virtude de grande parte da Matemática da civilização egípcia basear-se em papiros, as necessidades práticas influenciaram a invenção do calendário, a construção de pirâmides e outros monumentos grandiosos. Essa síntese é ressaltada por Boyer (2003, p. 2 apud Rossetto, 2013, p. 22) ao dizer que
os egípcios foram os primeiros a utilizar um calendário, tomando por referência o sol. Interessados em Astronomia, puderam observar que as enchentes do Nilo eram separadas em 365. Dessa observação surgiu o calendário, que é dividido em 12 meses de 30 dias. Além do calendário, os egípcios construíram as pirâmides de Gizé, monumentos avançados para a época” (Boyer, 2003, p. 2 apudRossetto, 2013, p. 22).
Em face dos conhecimentos matemáticos obtidos pelos egípcios, a Geometria egípcia ocorre a partir das medições, como afirma Ferreira (2016):
a Geometria egípcia teve suas origens na medição de terras. Nas fontes históricas matemáticas da civilização egípcia há problemas relacionados à medição de terras e, a partir de uma necessidade de calcular áreas de terrenos e volumes, havia um sentido prático para tais coisas (Ferreira 2016, p. 16).
Do ponto de vista astronômico, o estudo da Geometria teve sua contribuição para o desenvolvimento da humanidade. Segundo Bandeira (2017, s/p), “a Astronomia se desenvolveu como um ramo da Matemática precisamente com os gregos, mudando então a forma de pensar sobre os astros celestes”. Com os estudos astronômicos a partir dos movimentos celestes, foi possível criar o calendário, dividir o tempo em horas, dias, meses e anos. Esses estudos também contribuíram para a construção de instrumentos náuticos devido à ocorrência da expansão marítima no século XV, como apontam Fernandes et al (2011, p. 63 apud Gonçalves, 2018, p. 20):
em se tratando de contribuição na construção de instrumentos para facilitar os navegadores, a Universidade de Lisboa, a partir do século XIII, destacou-se na construção de três instrumentos náuticos importantíssimos, ajudando de forma considerável os homens ao mar: a balestilha, o quadrante e o astrolábio náutico (Fernandes et al., 2011, p.63 apudGonçalves, 2018, p. 20).
Entretanto, esses instrumentos foram construídos baseados em cálculos relacionados ao estudo da Trigonometria, em determinar medidas de alturas e distâncias, realizado por grandes filósofos matemáticos como Tales de Mileto, Pitágoras, Hiparco, Arquimedes, Ptolomeu e outros. Atualmente, cálculos como esses são utilizados em triângulos retângulos para medir distâncias, comprimentos e profundidades de locais de difícil acesso. Nesse sentido, percebemos que a Matemática foi pioneira para o desenvolvimento da Astronomia segundo o estudo da Geometria e da Trigonometria. Isso significa que, independentemente do ramo que a procede, a Matemática sempre deixa sua contribuição no âmbito social. Além disso, Mol (2013) a considera uma disciplina indispensável para a formação do cidadão, porque no mundo atual, mesmo tendo diversos campos que abrangem a aplicação da Matemática, os modelos matemáticos influenciam não só nas questões sociais e econômicas, mas também as questões científicas, promovendo o avanço tecnológico e conceitual de outras áreas da ciência, como frisa Gayo (2012).
Em todas as partes, a Matemática foi fundamental para a evolução do homem, seja pela busca por soluções de problemas diários ou para desvendar o oculto existente no universo. Todavia, para melhor compreender o significado da Matemática, a metodologia de ensino influencia diretamente o aprendizado, sendo essencial para a construção do conhecimento. Assim sendo, serão apresentadas a seguir a busca e o progresso por uma melhoria da qualidade do ensino da Matemática no seu contexto histórico.
A metodologia de ensino como ferramenta central
“Deixei de gostar de Matemática depois que o x deixou de ser sinal de multiplicação” (William Shakespeare). Essa frase reflete a realidade de muitos quando o assunto é Matemática, principalmente quando as operações são compostas por incógnitas envolvendo uma variedade de técnicas e procedimentos a fim de encontrar o resultado final. Por desempenhar papel construtivo na sociedade, é importante que o aluno enxergue a Matemática como elemento que favorece o desenvolvimento do raciocínio. Entretanto, para que isso ocorra é importante que o educador apresente mecanismos que conectam a Matemática à realidade, para que ela apresente sentido lógico, isto é, o processo de ensino está relacionado a técnicas e materiais adequados utilizados pelo professor de modo que o aluno possa compreender os conceitos expostos e, assim, organizar as ideias enxergando uma solução para aquele problema. Nesse ponto de vista, Moysés (1997, p. 67 apud Thomaz, 2017) conclui:
Se professor e alunos se defrontam com sentenças, regras e símbolos matemáticos sem que nenhum deles consiga dar sentido e significado a tal simbologia, então a escola continua a negar ao aluno (...) uma das formas essenciais de ler, interpretar e explicar o mundo.
A par dessa ideologia, a utilização de recursos pedagógicos e tecnológicos vem sido realizada como complemento metodológico na didática na tentativa de amenizar a dificuldade de aprendizagem e ao mesmo tempo criar condições para que o aluno desenvolva conhecimentos por meio de pensamentos lógicos e dedutivos. Entretanto, tais recursos precisam estar integrados a situações que conduzam ao estudo da análise e reflexão da atividade matemática. Em virtude disso, pressupomos que o aluno, além de desenvolver habilidades para cálculos e resolução de problemas, estará apto para estabelecer relações, analisar, debater ideias e concluí-las a partir de recursos didáticos integrados aos conhecimentos matemáticos. Ainda no que diz respeito ao processo de ensino-aprendizagem, o professor não deve ser apenas agente transmissor de conhecimento para o aluno receptor.
Por muitos anos, o ensino da Matemática seguia um método memorizador de ensino. Com isso, Fuchs et al. (2014) salientam que “o ensino, por sua vez, era livresco e centrado no professor, o qual tinha a função de expor e transmitir os conteúdos prontos e acabados, já descobertos e sistematizados nos livros didáticos” (p. 50). Com o objetivo de melhorar a qualidade de ensino, as tendências pedagógicas ganharam destaque nos meios educacionais por um longo período. O tipo de ensino mencionado anteriormente remete ao modelo de ensino tradicional, caracterizado pela tendência formalista clássica ocorrida na década de 50, sob uma metodologia baseada na memorização, sem se preocupar de fato se o aluno estava aprendendo ou não, cabendo ao aluno não mais que memorizar, repetir e obedecer. Além disso, Brum (2012) destaca que o modelo tradicional de ensino-aprendizagem não apresenta estímulo aos alunos, referindo que:
a Matemática historicamente na forma tradicional de ensino está unida a uma falsa consciência individualista, de dominação e reprodução de desigualdades sociais. Nessa perspectiva, de um lado são muitos os alunos em todos os níveis de ensino que consideram a Matemática inútil e sentem-se incapazes de aprender (Brum, 2012, p. 1).
Em oposição ao modelo de ensino mecanizado, surgem novas tendências mais centralizadas nos alunos. Por exemplo, no ensino da Matemática, as Tendências Histórico-Crítica e Socioetnocultural apresentaram uma visão mais significativa, atribuindo sentido e significado às ideias matemáticas, proporcionando a capacidade de pensar e estabelecer relações a partir de problemas reais, como relatam Piovesan et al (2008):
A tendência histórico-crítica concebe a Matemática como “um saber vivo, dinâmico, construído historicamente para atender às necessidades sociais e teóricas. Nessa tendência, a aprendizagem da Matemática não consiste apenas em desenvolver habilidades, como calcular e resolver problemas ou fixar conceitos pela memorização ou listas de exercícios, mas criar estratégias que possibilitam ao aluno atribuir sentido e construir significado às ideias matemáticas de modo a tornar-se capaz de estabelecer relações, justificar, analisar, discutir e criar” (Piovesan et al., 2008, p. 7).
Nesse sentido, Oliveira (2017) afirma que o professor deve ser visto como agente mediador orientador, que estimule o pensamento lógico-dedutivo do aluno, considerando que no antigo sistema de ensino tradicional o ato educacional era centrado no professor e que a didática consistia em “repetições” e o aluno apenas memorizava aquela informação sem o menor sentido, atitude que desqualifica o papel do educador. Todavia, o objetivo das tendências é destacar os meios educacionais ocorridos ao longo dos anos e, com isso, buscar promover a melhoria da qualidade de ensino. Gayo (2012) enfatiza que a busca pela melhoria de ensino da Matemática envolve um conjunto de ações que englobam questões sociais e políticas. Para ele,
distinguir as características das diferentes tendências exige muito estudo e compreensão das mudanças sociais e políticas, bem como dos diferentes valores e finalidades que são atribuídos ao ensino da Matemática e à relação entre professores e alunos (Gayo, 2012, p. 181).
Gayo (2012) salienta ainda que as diversas tendências que buscavam modernizar o ensino da Matemática deram início ao Movimento da Matemática Moderna, ocorrido em meados dos anos 1960. Segundo ele, esse movimento foi protagonista da unificação de Geometria, Álgebra e Aritmética em um único currículo. Em meio a esse movimento, destacava-se a Tendência Formalista Moderna, caracterizada por um ensino mais severo que valorizava o pensamento lógico-dedutivo. Gayo (2012, p. 182) acrescenta que
essa tendência buscava enfatizar a apreensão das estruturas subjacentes ao conhecimento matemático, pois, dessa forma, o aluno estaria capacitado a aplicar tais conteúdos dentro e fora da Matemática. Ficavam em segundo plano as aplicações e o caráter prático da disciplina (Gayo, 2012, p. 182).
Contudo, ao se referir à Matemática como uma construção humana, a História da Matemática se faz presente em algumas tendências, ao defini-la como ferramenta importante no processo de aprendizagem. Nesse caso, as tendências socioculturalista e histórico-crítica valorizam as questões sociais e culturais, reconhecendo que todo conhecimento faz parte de uma construção histórica.
Sendo assim, ao fazer uma análise dessas tendências, em busca de alternativas para práticas matemáticas em meio a circunstancias culturais, surgiu a Etnomatemática, termo difundido pelo grande matemático brasileiro Ubiratan D’Ambrosio. Ao deferir a Matemática como uma construção humana, D’Ambrosio (1999, p. 97 apud Chaquiam, 2017, p. 16) diz que
as ideias matemáticas comparecem em toda a evolução da humanidade, definindo estratégias de ação para lidar com o ambiente, criando e desenhando instrumentos para esse fim, e buscando explicações sobre os fatos e fenômenos da natureza e para a própria existência. Em todos os momentos da história e em todas as civilizações, as ideias matemáticas estão presentes em todas as formas de fazer e de saber (D’Ambrosio, 1999, p. 97 apudChaquiam, 2017, p. 16).
Quanto aos conteúdos curriculares, de acordo com Gayo (2012, p. 178), D’Ambrosio enfatiza que “o ensino dos conteúdos cobrados nos currículos deve ser associado aos fatores históricos”, referindo que grande parte dos conteúdos permanecem no currículo apenas por tradição. Nessas condições, cabe analisar a variedade de relações desses conteúdos com o estudo da Matemática estabelecido em diferentes contextos, possibilitando a criação de situações problema, enfatizando os pontos mais ou menos relevantes em cada situação. Logo, tal medida servirá de base para observar o nível de compreensão de cada aluno, considerando que cada situação será julgada em diferentes pontos de vista.
Na perspectiva de analisar os métodos de ensino atuais centrados na ação pedagógica, na concepção da Matemática e do conhecimento matemático, infere-se que existem várias formas de ensinar Matemática. E mesmo que existam desafios a serem enfrentados e solucionados, a busca pela melhoria de ensino da Matemática tem sido constante.
Resultados e discussões
A realização deste trabalho submete a investigação de elementos que possam complementar a prática pedagógica do ensino da Matemática ao processo de ensino-aprendizagem. A busca pela melhoria do ensino de Matemática vem sendo questionada ao longo dos anos e tem sido tema de diversos trabalhos científicos. Por essa razão buscamos esclarecer e responder: quais são as possíveis causas que levam à dificuldade de aprendizagem da Matemática, bem como os métodos que estão sendo utilizados para sanar esse problema? Apresentamos questões conceituais mais aprofundadas sob o olhar de outros autores buscando enfatizar os conceitos textuais do desenvolvimento da Matemática desde sua origem até os dias atuais. Com isso, o processo de investigação permitiu conjecturar que, devido à complexidade que o estudo da Matemática carrega, a falta de conexão com num contexto de resolução de problema impede que o aluno desenvolva capacidade de lidar com a atividade matemática, promovendo a dificuldade de aprendizagem. Entretanto, a metodologia de ensino empregada pelo professor também influencia a aprendizagem, visto que procedimentos adotados em diferentes décadas assumiram papel ineficaz para o desenvolvimento intelectual do aluno, destacados nas tendências educacionais. Dessa forma, o acúmulo de informações por um ensino mecanizado resultou em um processo de aprendizagem por repetição, e com isso influenciou a busca pela melhoria de ensino através do Movimento da Matemática Moderna. Esse movimento intensificou o ensino da Matemática, modernizou o currículo escolar e influenciou o uso da História da Matemática no processo de ensino-aprendizagem, objetivando também novas propostas alternativas para ação pedagógica, como a Etnomatemática.
Por essa e outras razões, a utilização da História da Matemática é reconhecida como elemento potencializador no processo de ensino-aprendizagem, pois demonstra como teorias e práticas foram criadas, proporcionando a concepção da Matemática através da história. Os recursos didáticos, ainda que seja uma alternativa agregar recursos pedagógicos e/ou tecnológicos que empregam informação necessária para auxiliar na compreensão da Matemática, podem e devem ser utilizados para facilitar o conteúdo e despertar habilidade, entendimento e criatividade nos alunos.
Outro fator importante nesse processo de ensino-aprendizagem é o papel do professor, pois ele irá exercer as funções metodológicas e epistemológica, ou seja, criar condições para que o aluno aprenda a partir do seu conhecimento científico. Nesse caso, o papel do professor é abrangente, pois durante o processo de ensino-aprendizagem ele precisa ser estimulante, interativo, perceptivo, criativo e procurar conhecer as condições socioculturais do indivíduo. Com isso, esperamos que o resultado desta pesquisa proporcione aos leitores uma visão mais ampla sobre a importância da Matemática em nossas vidas e que os dados aqui apresentados possam contribuir positivamente para o ensino da Matemática, principalmente na didática em sala de aula.
Considerações finais
A luta pela sobrevivência contribuiu significativamente para o desenvolvimento da Matemática no mundo. A partir da História, foi possível compreender que o conhecimento matemático deriva de um longo processo multicultural.
Embora a Matemática possa ser considerada um grande obstáculo por trazer consigo em suas etapas alto rigor de raciocínio e fundamentação teórica, é possível mostrar que introduzir a História da Matemática na didática em sala de aula pode se tornar um grande aliado para o processo de ensino-aprendizagem, enriquecendo a metodologia e concedendo uma visão mais ampla do conceito matemático em relação ao mundo, e, dessa forma, conectar a Matemática com a realidade, mostrando que essa disciplina não foi uma invenção, mas sim uma descoberta presente que se ocultava no universo.
Quanto à metodologia, acreditamos que a verdadeira aprendizagem é aquela introduzida na realidade, buscando conceitos e métodos que elevam o pensamento cognitivo do aluno. Mesmo sabendo que é um grande desafio conectar a Matemática com a realidade, o professor precisa buscar métodos inovadores ao apresentar sua didática. A utilização de recursos didáticos adequados ao conteúdo, além de amenizar a defasagem no processo de ensino, possibilita ao aluno compreensão necessária para abstrair melhor a Matemática em diversos ângulos. Por fim, considerando todos os argumentos aqui apresentados no decorrer da pesquisa, podemos inferir que, embora o ensino de Matemática tenha progredido nos últimos anos, ainda há muito a se fazer. Enquanto isso, é preciso inovar a didática com recursos e estratégias que vão além da sala de aula, mostrando a Matemática em diversos campos da atividade humana.
Referências
BANDEIRA, E.A importância da Matemática para a Astronomia. Astronomia Real, 2017. Disponível em: https://astronomiareal.wordpress.com/ 2017/01/10/ a-importancia-da-matematica-a-astronomia/. Acesso em: 25 out. 2020.
BARASUOL, F. F. A Matemática da Pré-História ao antigo Egito.UNI Revista, São Leopoldo, v. 1, nº 2, 2006.
BOYER, C. B.; MERZBACH, U. C. História da Matemática. São Paulo: Blucher, 2012.
BRUM, M. A. Tendência Pedagógica na Educação Matemática Escolar: segundo estudos de Fiorentini. Escola de Inverno de Educação Matemática: 1º ENCONTRO NACIONAL PIBID – Matemática, 2012.
CHAQUIAM, M.Ensaios Temáticos: História e Matemática em sala de aula. Belém: SBEM, 2017.
FERREIRA, M. L. Uma análise dos métodos empregados pelos egípcios para quadratura do Círculo. João Pessoa: SBEM, 2016.
FUCHS, M. J. et al. A história do ensino da Matemática: Contribuições na formação de futuros professores de Matemática. 93ª ed. Ijuí: Unijuí, 2014.
GAYO, J. Fundamentos e História da Matemática. Indaial: Centro Universitário Leonardo da Vinci – Uniasselvi, 2012.
GONÇALVES, R. M. A Trigonometria e a História da Matemática em sala de aula: uma experiência com a construção de instrumentos de navegação e do relógio de sol.Porto Alegre: Universidade Federal do Rio Grande do Sul, 2018.
KASHIWAKURA, C. T. et al. Frases que revolucionaram o Ensino da Matemática. São Paulo, 2013. Disponível em: https://cleliakashiwakura.wordpress.com/ Acesso em: 20 out. 2020.
MIYASCHITA, W. Y. Sistema de numeração: como funcionam e como são estruturados os números. Bauru, 2002.
MOL, R. S. Introdução à História da Matemática. Belo Horizonte: CAED/UFMG, 2013.
OLIVEIRA, D. A. U. As grandes navegações: aspectos matemáticos de alguns instrumentos náuticos. João Pessoa: Universidade Federal da Paraíba, 2017.
PARANÁ. Secretaria de Estado da Educação. Superintendência da Educação. Departamento de Ensino Fundamental. Orientações Pedagógicas, Matemática: sala de apoio à aprendizagem. Curitiba: SEED-PR, 2005.
PIOVESAN, S. B. et al. O ensino e aprendizagem da Matemática por meio da metodologia de resolução de problemas: algumas considerações. Paraná: PDE, 2008.
ROSSETTO, H. H. P. Um resgate histórico: a importância da História da Matemática. Medianeira: Universidade Tecnológica Federal do Paraná, 2013.
SILVA, K. I. História da Matemática: os primeiros indícios dos números. Campina Grande: Universidade Estadual da Paraíba, 2014.
THOMAZ, P. H. B.; MEGID, M. A. B. A. Recursos didáticos no ensino da Matemática: o jogo como estratégia de ensino e o programa ler e escrever. Currículo sem Fronteiras, 2017. Disponível em: http://www.curriculosemfronteiras.org/vol17iss3articles/thomaz-megid.pdf Acesso em: 24 out. 2020.
Publicado em 26 de outubro de 2021
Como citar este artigo (ABNT)
POMBO, Taciana Rodrigues. A concepção da Matemática através da história. Revista Educação Pública, v. 21, nº 39, 26 de outubro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/39/a-concepcao-da-matematica-atraves-da-historia
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

