A importância da metodologia de Resolução de Problemas nas aulas de Matemática e o que presumem professores da rede municipal de Alhandra/PB sobre o tema
Claudemir Galdino de Barros
Licenciado em Matemática (FFPG), especialista em Metodologia do Ensino de Matemática (Uninter), pós-graduando em Ensino de Ciências e Matemática (IFPB), professor do município de Alhandra/PB e da rede estadual de Pernambuco
Suemilton Nunes Gervázio
Doutor em Educação, professor (IFPB)
Aprendizagem matemática
A aprendizagem da Matemática nas escolas tem sido tem sido um desafio se para os professores ao longo dos tempos. As pesquisas e avaliações mais atuais, como, por exemplo, os resultados do Programa Internacional de Avaliação de Estudantes (PISA) e Sistema de Avaliação da Educação Básica (SAEB) têm mostrado que o aprendizado desse componente curricular tem sido insatisfatório.
Na contramão dessa fragilidade educacional, surgem diversas metodologias de ensino que visam tornar o conhecimento matemático mais democrático e eficiente, ou pelo menos, mais propício a suprir as exigências da sociedade atual. Ao pesquisar e fazer uma revisão bibliográfica, encontra-se uma gama de didáticas, como, por exemplo, a Aprendizagem Baseada em Problemas, a Aprendizagem Baseada em Projetos, a Modelagem Matemática, que prometem tal feito.
Pesquisas apontam que, dentre as várias possibilidades, as metodologias de ensino respaldadas na Aprendizagem Baseada em Problemas (PBL) acredita-se, após muitas pesquisas e leituras sobre as metodologias de ensino que se respaldam na Aprendizagem Baseada em Problemas (PBL), possam dar contribuições para a construção do conhecimento, como abordada por Paulo Freire, patrono da Educação brasileira, em suas obras.
Nesse sentido, no que concerne à instrução matemática, se traz para a discussão e reflexão a metodologia de Resolução de Problemas, abordada por George Polya (1995) em seu livro A arte de resolver problemas, como um processo possibilitador da aprendizagem. É importante destacar que a PBL tem se tornado um tema muito relevante na atualidade, pois ao ser diluído nos processos de ensino e aprendizagem das componentes curriculares, tal método tem produzido resultados satisfatórios, como pode ser observado em Souza e Dourado (2015).
Ainda se enfatiza, em relação à PBL, que a teoria que envolve tal método se aproxima bastante do que Polya (1995) sustenta como processo de ressignificação da aprendizagem matemática. E, nesse contexto, cita-se Redling (2011); esse autor afirma que os problemas matemáticos têm ocupado um lugar central na Matemática desde a Antiguidade. E que, portanto, é crucial retomar esta prática de ensino.
Em contrapartida, Onuchic (1999), citada por Redling (2011), declara que a importância dada à Resolução de Problemas pelos educadores matemáticos se deu somente a partir das décadas de 1980 e 1990, momento na qual se passaram a aceitar a ideia de que o desenvolvimento da capacidade de resolver problemas merecia atenção.
Ainda de acordo com Redling (2011), no final dos anos 1970, a Resolução de Problemas emerge, ganhando espaço no mundo inteiro. Discussões no campo da Educação Matemática, no Brasil e no mundo, evidenciam a necessidade de se adaptar o trabalho escolar às novas tendências que poderiam levar a melhores formas de ensinar e aprender Matemática.
Como já apresentado, a Resolução de Problemas tem-se mostrado uma metodologia muito importante para o processo de ensino e aprendizagem nas diversas áreas do conhecimento. No que tange à Matemática, o professor deve desenvolver diversas estratégias e metodologias para proporcionar a construção do conhecimento em seus alunos. Nesta perspectiva, acredita-se que a Resolução de Problemas contribui para que o aluno desenvolva um pensamento reflexivo e crítico sobre aquilo que está estudando.
Conforme Vianna (2002 apud Redling, 2011), a utilização da Resolução de Problemas em sala de aula ajuda a contribuir para o desenvolvimento da capacidade do aluno para elaborar perguntas e formular conjecturas, ou seja, exige uma participação ativa no que diz respeito à comunicação, expressão e seu modo de pensar, trabalhar em grupo e principalmente possibilitar o desenvolvimento da habilidade de fazer generalizações.
Com isso, essa pesquisa foi desenvolvida partindo dessas ponderações, de inquietações acerca das dificuldades apresentadas pelos alunos na aprendizagem matemática e na aversão de muitos por essa disciplina. A mesma foi aplicada a professores das turmas do Ensino Fundamental, anos finais, das escolas que compõem a rede de Ensino Municipal da cidade de Alhandra/PB.
O trabalho assim originou-se a partir dessas observações. Entre as quais destacamos a desmotivação dos alunos nas aulas de Matemática, a falta de aprendizagem e a necessidade de uma metodologia de ensino mais eficiente.
Deste modo, o ponto central de discussão do trabalho é analisar e discutir as potencialidades da Resolução de Problemas como uma metodologia eficaz, no que tange a construção do conhecimento matemático, sobretudo se o contexto abordado nos problemas estiver relacionado com o cotidiano dos discentes. Além disso, buscou-se também verificar o que acreditam alguns professores de Matemática a respeito desse tema, verificar se estes compreendem de fato os preceitos e definições que embasam tal metodologia e se eles as utilizam em suas práticas docentes.
A metodologia da Resolução de Problemas e sua importância para o ensino e aprendizagem de Matemática
A Resolução de Problemas é um processo desencadeador de conhecimentos difundido há bastante tempo. Ravagnani e Marques (2017, p. 36) acreditam que ela começou a fazer parte da Humanidade muito antes da existência dos números. Para estes autores, “os primeiros homens se depararam com problemas da vida cotidiana e tiveram que desenvolver métodos para resolvê-los. Com isso, criaram maneiras de comparar, quantificar, ordenar e medir, a fim de resolver seus problemas”.
Cabe agora definir o que de fato é um problema, para que assim se consiga apresentar e dissertar sobre a Resolução de Problemas e, em seguida, adotá-la como metodologia de ensino da Matemática. Para tanto, é trazido inicialmente Dante (1991, p. 9 apud Ravagnani; Marques, 2017). Tal autor define problema como qualquer situação que exija o pensar do indivíduo para solucioná-lo.
Para Pereira (1980, p. 28), citado por Ravagnani e Marques (2017), um problema é toda situação na qual o indivíduo necessita obter novas informações e estabelecer relações entre elementos conhecidos e os contidos num objetivo a que se propõe a realizar para atingi-lo. Já para Onuchic (1999), citado por Redling (2011, p. 18), “problema é tudo aquilo que não se sabe fazer, mas que se está interessado em resolver”.
De acordo com Redling (2011, p. 18), “problema é qualquer situação para a qual o aluno não dispõe de um método imediato de Resolução, mas que desperte seu interesse e estimule-o a pensar”. Já Polya (1986) considera que um indivíduo está diante de um problema quando este se depara com uma questão a que não pode dar a resposta, ou quando não sabe resolver usando seus conhecimentos, enquanto Mendonça (1993) trata o problema como uma situação conflitante que não apresenta solução clara e imediata, onde o sujeito deve elaborar as possíveis resoluções de forma original para chegar à solução.
Ainda sobre essa definição, Pozo (1998) indica que um problema difere de um exercício, pelo fato de que para este dispõe-se de procedimentos que levam de maneira imediata à Resolução. Porém, é possível que uma mesma situação seja um problema para uma pessoa e para outra um simples exercício, se esta possuir conhecimentos para resolvê-la. Já Nereide Saviani (2000), citado por Redling (2011, p. 25), relata que um problema não pode ser encarado como algo que é simplesmente desconhecido pelo homem; para essa autora, um problema é definido como “algo que não conhecemos, mas que temos a necessidade intencional de conhecer”.
Com isso, verifica-se que todas essas definições, atribuídas por esses autores, convergem em alguns pontos e divergem em outros. No entanto, todas elas referem-se ao fato de um problema ser uma situação que requer um processo cognitivo inteligível capaz de solucioná-lo ou pelo menos produzir sinapses que conduzam a caminhos para a elucidação. Já as divergências se dariam pelo fato de “alguns autores adotarem como referência a relação do indivíduo com a situação, enquanto outros dedicam a sua atenção para as características da própria tarefa” (Redling, 2011, p. 25).
Com base nessa definição, o diálogo visa agora ao método de Resolução de Problemas. Apesar de sua importância, tal tema só entrou em pauta de discussão mais efetivamente depois de uma recomendação feita em 1980 no documento “Uma agenda para a ação” do NCTM (National of Teachers of Mathematics), que é um conselho nacional dos professores de Matemática dos Estados Unidos. Ravagnani e Marques (2017) apontam que esse documento tratava de uma recomendação aos professores que propiciem em suas aulas situações que possibilitem processos de Resolução de Problemas como situação desencadeadora da construção de conhecimentos. Ou seja, resolver problemas deveria ser o foco do ensino de Matemática nas escolas.
Muito provavelmente, essa recomendação do NCTM teve como uma das fontes inspiradoras as ideias do matemático George Polya (1887-1985), apresentadas em seu livro A arte de resolver problemas, com primeira publicação em 1945 e que foi difundida por toda a comunidade acadêmica, tendo até hoje várias edições.
Essas recomendações influenciaram diretamente o Brasil, pois os Parâmetros Curriculares Nacionais – PCN foram construídos baseados no documento do NCTM. Os PCN, por sua vez, passaram a apostar na capacidade de resolver problemas, explorá-los, generalizá-los e até propor novos problemas a partir deles, como objetivos direcionais do ensino da Matemática. Além de indicar a Resolução de Problemas como ponto de partida das atividades matemáticas e discutir caminhos para se fazer Matemática na sala de aula.
Nesse contexto, é importante ressaltar que a Resolução de Problemas, enquanto técnica, pode ser abordada de três maneiras distintas: ensinar sobre a Resolução de Problemas, ensinar a resolver Problemas e ensinar fazendo uso da Resolução de Problemas. Para o contexto escolar, esta última é a abordagem mais adequada para a construção do conhecimento. Sobre isso, Andrade (1998), citado por Redling (2011, p. 19), afirma que “ao ensinar Matemática através da Resolução de Problemas, esta é concebida como uma metodologia de ensino, onde o problema é visto como um elemento contribuinte do processo de construção do conhecimento”.
Corroborando essa linha de pensamento, defendem Ravagnani e Marques (2017), que
não tratamos a Resolução de Problema como mera aplicação dos conceitos previamente abordados, no qual o aluno lê o enunciado, identifica a questão e aplica uma fórmula, mas, sim, como um veículo para o processo de ensino-aprendizagem de conteúdos matemáticos (Ravagnani; Marques, 2017, p. 50).
Fazendo uma revisão bibliográfica a respeito desse tema, encontram-se muitos autores que defendem a importância da utilização da Resolução de Problemas em sala de aula. Por exemplo, Mandarino (2002), Onuchic (1999) e Carvalho (1994), que acreditam, entre outros fatores, que com a Resolução de Problemas, tem-se a oportunidade de propiciar o diálogo maior entre professor-aluno e aluno-aluno, na busca de soluções para os Problemas, promovendo um ambiente rico para aprender Matemática.
Outro fator importante no uso dessa metodologia é a possibilidade de desenvolver o processo de contextualização, abordando temas do contexto social dos educandos, dando sentido ao ato de ensinar e aprender. Conforme Ravagnani e Marques (2017),
a utilização da Resolução de Problemas é justificada enquanto meio de transformação de conhecimentos matemáticos abstratos em conhecimentos que dialoga com as práticas sociais e que fomenta o desenvolvimento cognitivo do indivíduo (Ravagnani; Marques, 2017, p. 38).
É importante destacar que na década de 1980 muitos materiais e recursos em Resolução de Problemas foram elaborados, contudo, devido às divergências em torno das diferentes concepções sobre o significado do termo “problema” como já discutido anteriormente, esses materiais não foram suficientes para alcançar um bom resultado.
Schroeder e Lester (1989), citados por Redling (2011), afirmam que ensinar através da Resolução de Problemas é a abordagem mais adequada, pois
o ensino de Matemática através da Resolução de Problemas nos oferece uma oportunidade de conhecer e delinear as dificuldades, de avaliar as capacidades e limitações do conhecimento matemático que os alunos possuem. O ensino através da Resolução de Problemas enfatiza os processos de pensamento, nas ações de aprendizagem além de trabalhar os conteúdos matemáticos, cujo valor não deve ser posto de lado. Também existe a possibilidade de o aluno formular Problemas tornando a Matemática um conhecimento mais próximo desse educando (Redling, 2011, p. 32-33).
Confirmando a Resolução de Problemas como uma importante metodologia, Romanatto (2008), citado por Redling (2011, p. 35), acrescenta que a Resolução de Problemas se apresenta como um dos caminhos mais promissores para o “fazer Matemática” dentro da sala de aula. Além disso, ele considera que “a Resolução de Problemas na Matemática deve abranger todos os níveis de ensino da Educação Básica, e os contextos dos problemas devem relacionar-se com situações da vida dos estudantes ou do dia a dia escolar, bem como as ciências do mundo do trabalho”.
Nesse contexto, Prediger, Berwanger e Mors (2009) citado por Gervázio (2019), alertam que um dos Problemas mais sérios no ensino da Matemática é que ela tem sido pensada e tratada por professores distantes da realidade do aluno. Ou seja,
julgamos ser essencial (entre outras atitudes) disponibilizar nas aulas de Matemática metodologias de ensino que instiguem os alunos a procurarem por si só os caminhos que os guiem à absorção dos conhecimentos, aos quais se pretende ensinar. Com esse intuito, acreditamos que as aulas que focam em Problemas do cotidiano, isto é, que tem relações diretas com a realidade, faz mais sentido para os alunos e tornam-se mais atrativas (Gervázio, 2019, p. 80).
Assim, acredita-se que a Resolução de Problemas é uma metodologia muito útil, pelo fato de ter a capacidade de potencializar a aprendizagem e, como apresentado por Rodrigues e Magalhães (2012, p. 1), ela pode mobilizar os saberes matemáticos no direcionamento de encontrar a solução para os problemas e “nessa busca, o aluno aprende a montar estratégias, raciocinar logicamente e verificar se sua estratégia foi válida, o que colabora para um amadurecimento das estruturas cognitivas”.
Portanto, o principal objetivo da metodologia da Resolução de Problemas na Matemática é desenvolver o raciocínio e não apenas chegar à resposta correta. Isso significa que, assim como Redling (2011, p. 33), a Metodologia de Resolução de Problemas também compartilha com as teses que indica que “o objetivo maior ao se trabalhar com a Resolução de Problemas na Matemática é levar o educando a entender a Resolução de Problemas como um processo, onde o principal interesse está no raciocínio desenvolvido e não somente na resposta encontrada”.
O papel do professor no uso da metodologia da Resolução de Problemas
A postura do docente em sala de aula também é pauta nas discussões quando se refere a aprendizagem Matemática. Porém, não só a atitude do professor, outros fatores também têm sido questionados, como, por exemplo, o ambiente da sala de aula, os materiais didáticos e o próprio sistema educacional. Isto é, “ensinar é uma ação complexa que depende em grande parte das personalidades envolvidas e das condições locais” (Polya, 1985, p. 11).
Nessa perspectiva, Gervázio (2019), defende que:
carecemos de um ensino que leve em consideração as várias vertentes que englobam todo o ambiente de aprendizagem escolar (o professor, o aluno, os conteúdos, os insumos disponíveis, entre outras). Caso essas variáveis não sejam consideradas, a probabilidade de falha em tal processo será enorme (Gervázio, 2019, p. 80).
Isso ressalta o quanto os professores têm um papel importante no processo de ensino e aprendizagem. São eles os primeiros a identificarem as dificuldades de cada aluno e assim encaminhar suas aulas na direção de suprir as necessidades encontradas, de forma a estimular os alunos, desenvolver e aprimorar o conhecimento. Isto é, “a atuação dos professores deve caminhar no sentido de proporcionar atividades e situações de aprendizagem que permitam aos alunos o desenvolvimento de conceitos e de processos que estimulem a capacidade de resolver problemas” (Redling, 2011, p. 19). E ainda mais,
cabe ao educador proporcionar um ambiente favorável, no qual o educando sinta-se motivado e estimulado a envolver-se nas situações propostas, de modo que ele o insira num processo criativo e reflexivo, que possibilite a tomada de decisões, o planejamento, a execução e a avaliação, visando à solução do problema (Redling, 2011, p. 33).
Nesse ambiente escolar, o professor deve proporcionar um espaço propício para utilizar a metodologia da Resolução de Problemas, onde seja possível ter um tempo adequado e que não haja competições na hora de resolver os problemas sugeridos. Na verdade, tal ambiente deve ser de cooperação, de procura, de exploração e descoberta (heurística), enfatizando que o mais importante são as estratégias e não o tempo gasto para resolvê-los ou a resposta final.
A aplicação da metodologia da Resolução de Problemas é uma tarefa difícil que exige do professor muita dedicação. De acordo com a concepção de Redling (2011, p. 39), “é de fundamental importância que o professor tenha consciência que um de seus principais deveres, é o de auxiliar seus alunos, o que não é uma tarefa fácil, uma vez que exige tempo, prática, dedicação e princípios firmes”.
Isso significa que, segundo as concepções de Nunes (2004 apud Redling, 2011), ao utilizar a metodologia da Resolução de Problemas, o papel do professor muda de “comunicador de conhecimento” para o de observador, organizador, consultor, mediador, controlador, incentivador da aprendizagem.
Nessa mesma linha de pensamento, Gervázio (2019, p. 79) defende que:
acreditamos que os professores devem assumir uma postura imprescindível, de docentes comprometidos com uma educação de qualidade, no sentido de minimizar as rupturas existentes entre a importância da aprendizagem Matemática e a compreensão dos conteúdos pelos alunos. Assim, implantar metodologias de ensino que evitem decorar fórmulas e promovam estratégias que conduzam a criação de tais fórmulas é uma atitude louvável.
Além disso, o professor deve considerar todas as respostas dadas pelos alunos, inclusive as respostas erradas, pois elas também são frutos de um raciocínio. Compreendendo esse raciocínio, o professor pode ajudar o aluno de uma forma melhor. Para Redling (2011, p. 39), “é necessário o professor reconhecer, aceitar e valorizar as possibilidades de resoluções criadas pelos alunos, para que assim eles se percebam ativos na construção da aprendizagem e desenvolvam a sua criatividade”.
Cabe ao professor ajudar os alunos, contudo de forma moderada, assim como defende Polya (1995), onde, segundo o mesmo,
o estudante deve adquirir tanta experiência pelo trabalho independente quanto lhe for possível. Mas se ele for deixado sozinho, sem ajuda ou com auxílio insuficiente, é possível que não experimente qualquer progresso. Se o professor ajudar demais, nada restará para o aluno fazer. O professor deve auxiliar, nem demais nem de menos, mas de tal modo que ao estudante caiba uma parcela razoável de trabalho (Polya,1995, p. 1).
Na verdade, o docente deve agir com muito discernimento, procurando entender como o aluno resolveria tal problema. Ou seja, “O professor deve colocar-se no lugar do aluno, perceber o ponto de vista deste, procurar compreender o que se passa em sua cabeça e fazer uma pergunta ou indicar um passo que poderia ter ocorrido ao próprio aluno” (Polya, 1995, p. 1).
Isso posto, acrescenta-se que, de fato, em se tratando da Resolução de Problemas enquanto metodologia de ensino e aprendizagem da Matemática, o papel do professor nesse processo é um dos mais importantes (talvez até o mais crucial). Ele é o articulador e mediador entre o conhecimento e o aluno, por isso tal tarefa não é trivial, ele tem o papel meticuloso de orientar os alunos por meio de indagações e direcionamentos, a procurar estratégias, elaborar conjeturas e produzir teses, isto é, instigar o conhecimento matemático.
As diretrizes curriculares nacionais, os PCN e a metodologia da Resolução de Problemas
É bastante recorrente, nos trabalhos e pesquisas que se referem à aprendizagem da Matemática escolar, encontrar muito desinteresse dos alunos por tal componente curricular. Os Parâmetros Curriculares Nacionais (Brasil, 1997), citados por Gervázio (2019), mencionam que a insatisfação revela que há problemas a serem enfrentados, tais como a necessidade de reverter um ensino centrado em procedimentos mecânicos, desprovidos de significados para o aluno.
Nesse mesmo contexto, Ponte (1994 apud Redling, 2011, p. 19) argumenta que
o insucesso relacionado ao processo de ensino-aprendizagem da Matemática para os professores em muito se deve à má preparação dos alunos desde o início da Educação Básica, aos currículos demasiadamente longos e à necessidade do seu cumprimento, obrigando-os a deixarem para trás os alunos mais “lentos”. Para os alunos, a principal razão do insucesso na disciplina resulta da dificuldade de compreensão dos seus conceitos e no fato de os professores não a explicarem muito bem, nem a tornarem interessante.
No entanto, é importante ressaltar que, apesar da importância creditada à metodologia de Resolução de Problemas, os PCN não a consideram como metodologia de ensino. Conforme Redling (2011),
contudo, os PCN não tratam da Resolução de Problemas admitindo os alunos como co-construtores do conhecimento, tendência marcada no período Pós-Polya. Há apenas o apoio para a utilização da Resolução de Problemas durante o processo de ensino-aprendizagem, mas não diretamente como metodologia (Redling, 2011, p. 40).
Apesar disso, a Resolução de Problemas como metodologia de ensino e aprendizagem tem-se mostrado muito promissora, dada a sua abrangência de aplicabilidade e, sobretudo, os frutos colhidos quando realmente aplicada de forma coerente com a realidade. Mas a sua implantação, de fato, ainda encontra desafios a serem superados. Segundo Redling (2011, p. 36), “apesar da ênfase dada à Resolução de Problemas enquanto Metodologia de Ensino-Aprendizagem na década de 1980, e dos avanços e apoio atuais, ainda há muitas barreiras a serem ultrapassadas para que ela seja utilizada no processo educativo”.
O ensino de Matemática no Brasil tem encontrado muitos obstáculos, os quais merecem destaque e devem ser resolvidos, para que se tenha um ensino de qualidade. Conforme os PCN, a formação dos professores e o seu exercício em sala de aula são exemplos desses obstáculos. Para Redling (2011, p. 37), “um problema sério a ser enfrentado para que seja possível uma reforma do ensino como pretendida pelos PCN reside na formação dos professores e em seu trabalho em sala de aula. Freitas (2002), citado por Redling (2011, p. 37), aborda que
nenhuma intervenção no processo de ensino-aprendizagem pode fazer mais diferença do que um professor bem formado, inteligente e hábil. A formação do professor tem um efeito direto na aprendizagem dos alunos, pois ninguém despende tanto tempo ou tem tanta influência sobre os alunos quanto os próprios docentes.
Em suas conjecturas, Redling (2011, p. 41) argumenta que, em se tratando da dificuldade de aplicação da metodologia da Resolução de Problemas “não se resolve sugerindo aos professores instruções mais específicas por meio de manuais ou cursos. É indispensável, portanto, uma profunda mudança na formação tanto inicial como continuada dos professores”.
Assim, acredita-se que o sucesso da aplicabilidade da Resolução de Problemas deve estar estreitamente associado à inserção desse tema nos projetos políticos do curso (PPC), os quais devem levar em consideração o contexto em que a instituição superior de ensino se encontra. Ou seja,
a abordagem de Resolução de Problemas deve ser explicitada nos PPC de cada curso, considerando a realidade social em que a IES (instituição de ensino superior) estiver inserida, mas sempre como ferramenta didática privilegiada; a abordagem de Resolução de Problemas está intimamente ligada aos conceitos que devem ser trabalhados, às habilidades esperadas dos alunos na educação básica e, portanto, á mudança de paradigma na educação Matemática brasileira (Ravagnani; Marques, 2017, p. 49).
Metodologia
Buscando alcançar os objetivos da pesquisa, o referido projeto foi desenvolvido inicialmente fazendo uma revisão bibliográfica para que se fosse compreendida a teoria que envolve a Resolução de Problemas, enquanto metodologia de ensino da Matemática. Posteriormente, apoiando-se nas bibliografias consultadas, recorreu-se à pesquisa de campo, com o intuito de analisar e discutir brevemente o que acreditam alguns professores de Matemática a respeito desse tema, questionar se estes compreendem de fato os preceitos e definições que embasam tal metodologia e se eles as utilizam em suas práticas docentes.
A pesquisa de campo, segunda parte do trabalho, foi realizada a partir de um questionário composto por sete questões e aplicado a quatro professores de Matemática do Ensino Fundamental II da rede municipal de educação da cidade de Alhandra/PB. Nessa etapa, os professores foram indagados acerca da sua formação, atuação profissional, suas práticas pedagógicas e a metodologia da Resolução de Problemas.
O instrumento utilizado para coleta dos dados foi um questionário on-line, por meio do Google Forms. Os professores pesquisados foram contactados de forma indireta, por telefone, e receberam o link para acessar as perguntas através do aplicativo de mensagens WhatsApp. Para a construção e aplicação dessa etapa do trabalho, tornou-se necessário consultar Lakatos (2010), que apresenta questionário como um instrumento de coleta de dados estruturado por uma série de perguntas que deverão ser respondidas por escrito sem a presença do entrevistador.
As perguntas apresentadas foram compostas de questões abertas e de múltipla escolha. Em tal etapa, não foram utilizadas técnicas de tratamentos de dados estatísticos, apenas uma exposição dos resultados com a amostra usada.
Resultados e discussão
A pesquisa foi realizada com quatro professores efetivos da cidade de Alhandra/PB, o que representa 66% do total de professores efetivos desse município que estavam em regência no período da pesquisa.
Inicialmente, a primeira pergunta do questionário indagava os professores sobre a sua área de formação. Aqui o objetivo foi identificar se eles eram formados em sua área de atuação, o que ficou constatado, conforme se observa no gráfico a seguir.
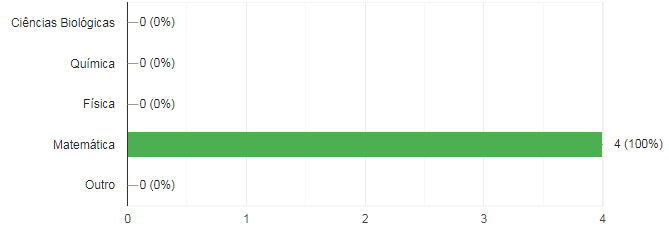
Gráfico 1: Área de formação dos professores
Ainda relacionado à formação, os pesquisados foram questionados na segunda pergunta sobre aperfeiçoamento profissional. Objetivava-se com essa indagação identificar se eles possuíam cursos complementares (pós-graduação), o que poderia indicar, em certa medida, a sua propensão em utilizar metodologias diferenciadas, que inclui a Resolução de Problemas. Como resultados, obteve-se que todos os professores pesquisados possuem ou estão cursando uma pós-graduação, como mostra o gráfico a seguir.
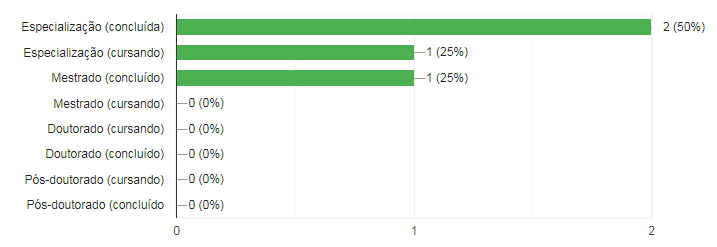
Gráfico 2: Formação complementar (pós-graduação)
Em seguida, na terceira pergunta, foram questionados sobre o tempo de atuação na educação e se trabalhavam apenas em escolas da rede pública ou também em instituições educacionais da rede privada. Os resultados coletados mostraram que todos eles trabalham há mais de 10 anos como docente e que a maioria exerce a sua docência apenas em escolas da rede púbica de ensino.
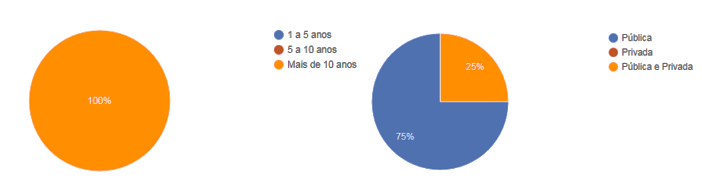
Gráfico 3: Tempo de exercício profissional e tipo de escola onde lecionam.
Os professores também foram questionados, na quarta pergunta, sobre o seu curso de graduação. Aqui se indagava sobre a grade curricular, se ela contemplava a disciplina de Metodologia do Ensino de Matemática ou equivalente e se eles gostaram do desenvolvimento dessa disciplina. Os resultados apresentados na imagem a seguir indicam que todos os entrevistados cursaram licenciatura e que tiveram bom aproveitamento.
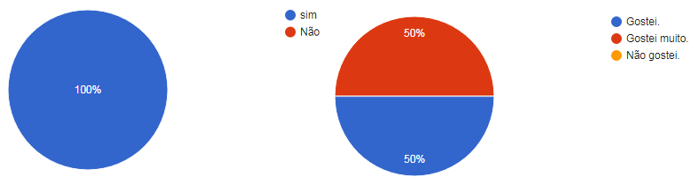
Gráfico 4: Estudou a disciplina de Metodologia do Ensino de Matemática? O que achou da disciplina?
Esses primeiros resultados mostram um cenário favorável ao uso da metodologia da Resolução de Problemas, uma vez que todos são formados na área que atuam, têm cursos complementares (pós-graduação), possuem muitos anos de experiência na docência, cursaram e gostaram da disciplina de Metodologia do Ensino de Matemática.
Em seguida, na quinta pergunta, os entrevistados foram indagados a respeito da sua carga horária semanal. Objetivava-se com isso inferir sobre a disponibilidade de tempo para o planejamento das aulas e, consequentemente, a organização de ações metodológicas mais efetivas. Nesse quesito, metade dos professores respondeu que trabalham até 30 horas/aulas e a outra metade respondeu que trabalha mais de 40 horas/aula por semana.
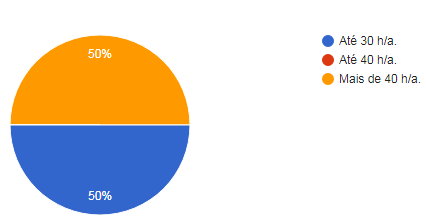
Gráfico 5: Carga horária semanal dos professores
Com esse resultado, conclui-se que esse fator é um ponto crítico, haja vista que a maioria dos professores tem uma carga horária de 30 ou mais de 40 horas/aula semanais, o que reflete diretamente na qualidade e implantação de novas metodologias de ensino e aprendizagem, como a de Resolução de Problemas. Visto que, para tal implantação, necessita-se de tempo para estudo e preparação dos materiais didáticos como a elaboração de problemas significativos.
Na sexta e penúltima pergunta, foi questionado sobre a metodologia de Resolução de Problemas. Sobre o tema, todos os professores afirmaram conhecer tal metodologia e três quartos deles declararam que a aplicam em sala de aula. Esses resultados são exibidos na imagem a seguir.
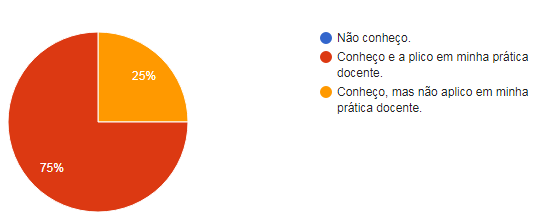
Gráfico 6: Você conhece a metodologia de Resolução de Problemas?
Finalizando, a última pergunta foi uma questão aberta: pediu-se aos professores que aplicam a metodologia da Resolução de Problemas em suas aulas, que apresentassem suas principais dificuldades em tal aplicação. Obtivemos os quatro apontamentos listados a seguir:
- Os alunos não entendem muito bem o português, a ponto de não conseguir interpretar os problemas;
- Os professores perdem muito tempo esperando as respostas;
- Os alunos adotam outras metodologias e acabam demorando para resolver os problemas;
- A resistência dos alunos a esse método de Resolução de Problemas, pois muitos não estão acostumados a trabalhar Matemática dessa forma.
Considerações finais
Neste trabalho, pôde-se observar, na prática docente do grupo pesquisado, que de fato a educação matemática nas escolas públicas municipais da cidade de Alhandra/PB precisa de mudanças, para que se tenha uma educação pública mais condizente com as necessidades dos estudantes. Contudo, essas mudanças não dependem só e exclusivamente dos profissionais que a executam no “chão da escola”, mas sim de todos os que estão inseridos no rol de atores que compõem a Educação.
A partir das análises dessa pesquisa como um todo, chega-se à conclusão de que a Resolução de Problemas aplicada à metodologia de ensino e aprendizagem é uma alternativa educacional que pode trazer bons resultados no que concerne à construção do conhecimento matemático do aluno.
Ao fazer o levantamento bibliográfico, constatou-se que diversos autores divergem quanto à definição do termo “problema”, porém quanto à sua importância para promover um ensino significativo, eles convergem para uma mesma direção.
Constatou-se também que as teorias atuais defendem uma didática docente mais dinâmica e eficaz e, nesse sentido, ensinar Matemática através da Resolução de Problemas indica ser uma aposta viável. Para tanto, a formação inicial e continuada do professor é de fundamental importância, pois possibilita a eles novas alternativas.
Em um dos objetos de estudo, a Resolução de Problemas nas aulas de Matemática na rede municipal da cidade de Alhandra/PB, percebeu-se que os professores possuem uma formação inicial e continuada na área que atuam e que conhecem e acreditam no potencial da Resolução de Problemas como metodologia de ensino. Contudo, nem todos os professores afirmaram que a aplicam em sala de aula, o que não é suficiente, de acordo com a pesquisa, pois não basta conhecer a metodologia, é preciso colocá-la em prática.
Relativamente à última questão do questionário da pesquisa de campo, um ponto destacado pelos professores e que merece ser analisado é a “perda de tempo”, o que por um lado revela uma visão equivocada, diante dos estudos feitos pelos autores consultados neste trabalho, como Redling (2011, p. 39), pois essa metodologia demanda tempo para a sua aplicação; já por outro lado, demonstra uma pressão sobre professores preocupados em ter de cumprir um extenso currículo durante o ano letivo. Assim, observa-se que, de certa forma, eles precisam de uma melhor formação acerca dessa metodologia, bem como de mais oportunidade de aplicá-la de maneira satisfatória no decorrer do ano letivo.
Por fim, outro ponto a ser destacado nas falas dos professores na última questão é “as outras metodologias” usadas pelos alunos na Resolução dos Problemas. No estudo outrora realizado, os teóricos defendem que os professores devem considerar todos os caminhos realizados pelos alunos, até as respostas erradas, como Redling (2011, p. 39). Portanto, esses caminhos diferentes apresentados na Resolução de Problemas não são e não devem ser encarados como um empecilho para a aplicação da metodologia aqui em questão, muito pelo contrário, esses caminhos devem ser usados como propulsores de conhecimento.
Referências
ANDRADE, S. Ensino-Aprendizagem de Matemática via Resolução, exploração, codificação e descodificação de Problemas. Dissertação (Mestrado) – Universidade Estadual Paulista, Rio Claro, 1998.
BRASIL. Ministério da Educação. Relatório técnico do Sistema Nacional de Avaliação da Educação Básica - SAEB, 2018. Brasília: Ministério da Educação/INEP, 2018.
CARVALHO, D. L. Metodologia do ensino da Matemática. São Paulo: Cortez, 1994.
DANTE, L. R. Didática da Resolução de Problemas. 3ª ed. São Paulo: Ática, 1991.
GERVÁZIO, Suemilton Nunes. A Heurística Matemática: uma aliada aos processos de ensino e aprendizagem. Tese (Doutorado em Educação Científica Matemática e Tecnológica) – Faculdade de Educação, Universidade de São Paulo, São Paulo, 2019.
GUÉRIOS, E., MEDEIROS JUNIOR, R. J. Resolução de problema e Matemática no Ensino Fundamental: uma perspectiva didática. In: BRANDT, C. F.; MORETTI, M. T. (Orgs.). Ensinar e aprender Matemática: possibilidades para a prática educativa [online]. Ponta Grossa: Editora UEPG, 2016.
LAKATOS, Eva Maria. Fundamentos de metodologia científica. 7ª ed. São Paulo: Atlas, 2010.
MANDARINO, M. C. F. Os professores e a arte de formular problemas contextualizados. 2002. Disponível em: http://www.bienasbm.ufba.br/OF12.pdf. Acesso em: 11 mar. 2021.
MENDONÇA. M. C. D. Problematização: um caminho a ser percorrido em Educação Matemática. Tese (Doutorado) – Universidade Estadual de Campinas, Campinas, 1993.
ONUCHIC, L. R. Ensino-aprendizagem de Matemática através da Resolução de Problemas. In: BICUDO, M. A. V. (Org.). Pesquisa em Educação Matemática: concepções & perspectivas. São Paulo: Editora Unesp, 1999. p. 199-218.
PEREIRA, W. C. de A. Resolução de Problemas criativos - ativação da capacidade de pensar. Brasília, Embrapa-DID, 1980.
POLYA, G. A arte de resolver problemas: um novo enfoque do método matemático. Trad. Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.
POLYA, G. O ensino por meio de problemas. Revista do Professor de Matemática, nº 7, p. 11-16, 1985.
POZO, J. I. (Org.). A solução de problemas: aprender a resolver, resolver para aprender. Porto Alegre: Artmed, 1998.
PREDIGER, Juliane; BERWANGER, Luana; MORS, Marlete Finke. Relação entre aluno e Matemática: reflexões sobre o desinteresse dos estudantes pela aprendizagem dessa disciplina. Revista Destaques Acadêmicos, ano 1, nº 4, 2009.
RAVAGNANI, J. A. D. C.; MARQUES, Amanda Cristina Teagno Lopes. George Polya e ensino de Matemática por meio da Resolução de Problemas nas Diretrizes Curriculares Nacionais para a formação de professores de Matemática. Posgere, v. 1, p. 30-53, 2017.
REDLING, Julyette Priscila. A metodologia de Resolução de Problemas: concepções e práticas pedagógicas de professores de Matemática do Ensino Fundamental. Dissertação (Mestrado em Educação para a Ciência), Universidade Estadual Paulista, Bauru, 2011.
RODRIGUES, A.; MAGALHÃES S. C. A Resolução de Problemas nas aulas de Matemática: diagnosticando a prática pedagógica. Revista Acadêmica Feol. Refeol., v. 1, nº 1, p. 1-16. 2011.
ROMANATTO, M. C. O livro didático: alcances e limites. 2008. Disponível em: http://www.sbempaulista.org.br/epem/anais/mesas_redondas/mr19Mauro.doc. Acesso em: 12 fev. 2021.
SAVIANI, N. Saber escolar, currículo e didática: problemas da unidade conteúdo/método no processo pedagógico. Campinas: Autores Associados, 2000.
SCHROEDER. T. L.; LESTER Jr., F. K. Developing understanding in Mathematics via Problem Solving. In: TRAFTON, P. R.; SHULTE, A. P. (Eds.). New directions for Elementary School Mathematics. EUA: National Council of Teachers of Mathematics, 1989.
SOUZA, C. S; DOURADO, Luís. Aprendizagem Baseada em Problemas (ABP): um método de aprendizagem inovador para o ensino educativo. Holos, Natal, ano 31, v. 5, 2015.
SOUZA, Joamir Roberto de. Matemática, realidade & tecnologia: 8º ano. São Paulo: FTD, 2018.
VIANNA, C. R. Resolução de Problemas. Temas em Educação, p. 401-410, 2002.
Publicado em 26 de outubro de 2021
Como citar este artigo (ABNT)
BARROS, Claudemir Galdino de; GERVÁZIO, Suemilton Nunes. A importância da metodologia de resolução de problemas nas aulas de Matemática e o que presumem professores da rede municipal de Alhandra/PB sobre o tema. Revista Educação Pública, v. 21, nº 39, 26 de outubro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/39/a-importancia-da-metodologia-de-resolucao-de-problemas-nas-aulas-de-matematica-e-o-que-presumem-professores-da-rede-municipal-de-alhandrapb-sobre-o-tema
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

