Medindo o tamanho da Lua pela observação de um eclipse lunar
Alessandro Martins
Doutor em Física. Professor Associado do curso de Física da Universidade Federal de Jataí (UFJ). Goiás
Phablo de Araujo Sousa
Aluno de Graduação do Curso de Física da Universidade Federal de Jataí (UFJ). Goiás
Medindo o Tamanho da Lua pela Observação de um Eclipse Lunar
O Brasil é um país que apresenta em seu território grandes disparidades socioeconômicas, o que influencia também na qualidade da educação como no caso do estudo das ciências, em especial da Astronomia, muito heterogêneo e que, nas regiões longe dos grandes centros populacionais, é pouco explorada por docentes e estudantes do Ensino Básico. A fim de contribuir para a redução desta deficiência, a astrofotografia tem sido considerada como uma importante ferramenta para auxiliar estudantes na aprendizagem da astronomia e ciências afins (Silva, 2016). Astrofotografia é uma técnica especializada de registro de imagens que consiste na aquisição de fotografias de corpos celestes, como estrelas, planetas, cometas, aglomerados de estrelas e galáxias, ou eventos como eclipses, trânsitos, entre outros. É uma excelente ferramenta para o ensino visual e experimental, cujos métodos ilustrativos ajudam os estudantes a se relacionarem mais facilmente com fenômenos astronômicos. Neste trabalho, apresentamos uma metodologia de determinação do raio da Lua, utilizando-se da análise e manipulação do registro fotográfico de um eclipse lunar total ocorrido em 21 de janeiro de 2019. Este registro foi realizado pelo projeto acadêmico ‘Redescobrindo a Astronomia’, vinculado à Universidade Federal de Jataí (UFJ).
A primeira estimativa dos tamanhos relativos da Terra e da Lua foi realizado por Aristarco de Samos (século III a.C.). Sua metodologia envolvia a observação do tempo de trânsito da Lua através do cone de sombra (umbra) projetado pela Terra durante um eclipse lunar. Comparando o tempo de trânsito com o tempo em que a Lua percorre uma distância igual ao seu próprio diâmetro, Aristarco determinou o tamanho do cone de sombra da Terra em termos do diâmetro lunar (Batten, 1981). A partir de uma única observação de eclipse lunar, Aristarco descobriu que o diâmetro da umbra representava duas vezes o diâmetro lunar. O valor médio atualmente aceito é de aproximadamente 2,65 diâmetros lunares, com registros obtidos para um eclipse lunar total com o caminho de trânsito da Lua atravessando o centro da umbra da Terra (Birriel, 2019).
Eclipses lunares são fenômenos astronômicos que ocorrem quando Sol, a Terra e a Lua se alinham quase que perfeitamente. Apesar do período orbital da Lua em torno da Terra ser de 27,32166 dias (mês sideral ) (Nasa, 2012), apenas três eclipses lunares ocorrem em média a cada ano. Isso se deve ao fato de a Lua possuir uma órbita inclinada em cerca de 5 graus em relação ao plano da órbita da Terra em torno do Sol. Desse modo, a Lua passa a maior parte do tempo acima ou abaixo do plano da órbita da Terra. E o plano da órbita da Terra em torno do Sol é importante porque as sombras da Terra estão exatamente no mesmo plano (Figura 1). Sendo assim, existem apenas dois pontos (nodos) onde os dois corpos celestes poderiam se alinhar ao Sol (as posições onde a Lua atravessa o plano orbital da Terra, conforme demonstrado na Figura 1.c). Um eclipse da Lua (ou eclipse lunar) só pode ocorrer na Lua Cheia e apenas se a Lua transitar por alguma parte da sombra da Terra. Essa sombra é na verdade composta de dois componentes em forma de cone, um aninhado dentro do outro. A sombra externa ou penumbra é uma zona onde a Terra bloqueia parte, mas não todos os raios do Sol de atingir a Lua. Em contraste, a sombra interna ou umbra é uma região onde a Terra bloqueia toda a luz solar direta de alcançar a Lua. Os eclipses lunares são classificados em eclipse lunar penumbral (a Lua transita pela penumbra), eclipse lunar parcial (uma parte da Lua transita a umbra) e eclipse lunar total (a Lua inteiramente transita a umbra). Cerca de 35% de todos os eclipses são do tipo penumbral, muito difíceis de observar, mesmo com o uso de um telescópio. Outros 30% são eclipses parciais, fáceis de visualização a olho nu. Os 35% restantes são eclipses totais, eventos maravilhosos de serem observados (Nasa, 2009). A aparência visual é algo importante que caracteriza um determinado tipo de eclipse. Os eclipses penumbrais são claros e difíceis de observação, a sombra penumbral da Terra forma um cone divergente que se expande no espaço na direção antissolar (Figura 1.a e 1.b). De dentro desta zona, a Terra bloqueia somente parte do disco solar, de modo que uma fração dos raios solares atingirá as superfícies mais eclipsadas da Lua. Eclipses parciais são observáveis a olho nu, pois quando uma parte do disco lunar se posiciona na umbra, surge um efeito de contraste (aparência mais escura), quando comparado com o brilho da porção restante na penumbra (cerca de 500 vezes maior). O tipo de eclipse lunar que provoca a maior atenção de observadores é o caracterizado como total. A aparência visual durante um eclipse lunar total varia ao longo do período de totalidade, devido à geometria do caminho da Lua através da umbra e ao efeito provocado pela atmosfera da Terra (Figura 2). Neste último caso, a atmosfera da Terra filtra, atenua e desvia alguns dos raios do Sol para a sombra. As moléculas na atmosfera terrestre espalham de forma mais intensa a luz de comprimento de onda curto (por exemplo, amarelo, verde, azul) do que a luz de comprimento de onda longo (laranja, vermelho), processo que caracteriza o tom avermelhado do “pôr do sol” (ocaso) e também confere aos eclipses totais a cor laranja avermelhada característica. A atmosfera atua como uma lente em forma de anel que refrata a luz solar de comprimento de onda da região do laranja ao vermelho na sombra umbral da Terra.
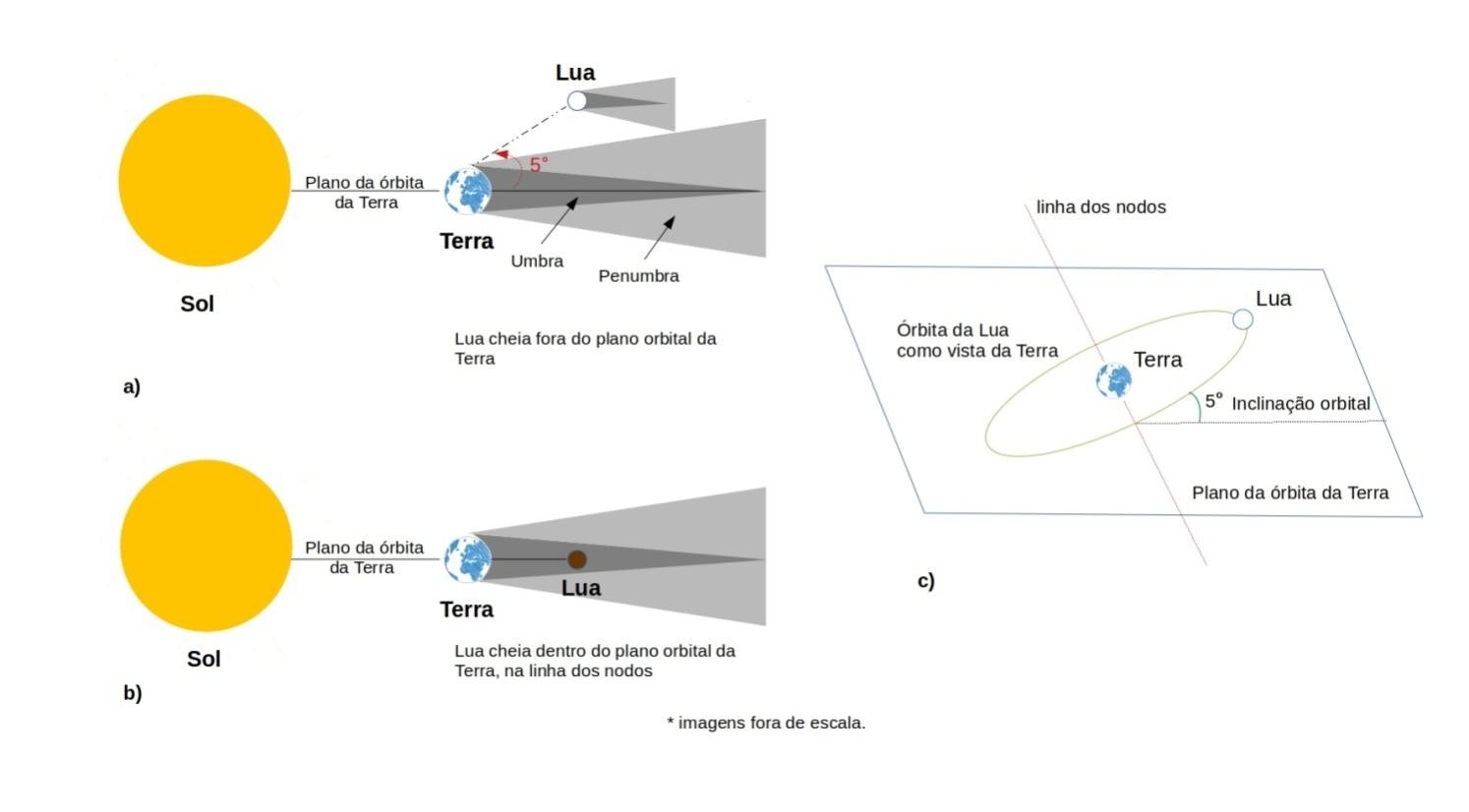
Figura 1: a) Durante a maioria dos meses, a Lua Cheia ocorre quando a Lua está inclinada em relação ao plano orbital da Terra, o que ocasiona a ausência de eclipse Lunar. b) Eclipse lunar total. c) Representação da órbita da Lua em relação ao plano da órbita da Terra

Figura 2: Diferenças na aparência visual da Lua durante o período de totalidade de um eclipse lunar total. Imagens obtidas durante o eclipse lunar total ocorrido em 21 de janeiro de 2019
Além do mês sideral, existem também outros três períodos orbitais conhecidos como mês sinódico, anomalístico e dracônico, cruciais para a compreensão e previsão de eclipses (Chalub, 2009). Esses períodos e os harmônicos entre eles determinam como, onde e quando os eclipses lunares ocorrem. O mês sinódico é quem governa as chamadas fases lunares. A Lua não é uma fonte de luz própria - o seu brilho é devido, principalmente, à reflexão da luz solar incidente sobre a sua superfície. Como consequência, a geometria de sua posição orbital em relação ao Sol e à Terra determina a fase aparente da Lua. O mês sinódico tem período de 29,53059 dias, ou seja, quase 2,21 dias a mais do que o mês sideral. Quando a Lua orbita em torno da Terra, ambos os objetos também progridem em órbita ao redor do Sol. Após completar uma revolução com referência às estrelas fixas, a Lua avançará um pouco mais ao longo de sua órbita para atingir a mesma posição inicial em relação ao Sol e à Terra. Isso explica por que o mês sinódico é mais longo do que o mês sideral. O mês anomalístico corresponde ao período de revolução da Lua em torno de sua órbita elíptica medida de perigeu (ponto da órbita da Lua mais próximo do planeta Terra) a perigeu, cujo valor médio é de 27,55455 dias. O mês dracônico baseia-se na característica de a órbita da Lua possuir um ângulo de inclinação em relação ao plano da órbita da Terra, sendo que a interseção desses planos define dois pontos ou nodos na esfera celeste, conforme já citado (ver Figura 1.c). Desse modo, o mês dracônico corresponde ao período entre dois trânsitos sucessivos da Lua pelo mesmo nodo, cujo período corresponde a 27,212220 dias. Devido ao torque exercido pela força gravitacional do Sol sobre o momento angular do sistema Terra-Lua, a linha dos nodos se processa na direção oposta àquela em que a Lua está orbitando a Terra, com uma rotação a cada 18,6 anos (Chalub, 2009). Como resultado, o tempo que a Lua leva para retornar ao mesmo nodo é menor que um mês sideral.
O intervalo de tempo entre dois eclipses lunares sucessivos pode ser de 1, 5 ou 6 lunações, geralmente são bem diferentes, ou seja, penumbral, parcial ou total. A periodicidade de um determinado eclipse lunar requer a reprodução dos mesmos parâmetros orbitais iniciais - condição satisfeita quando se obtém uma harmonia entre os meses sinódico, anomalístico e dracônico, ou seja, os dois eclipses ocorrem no mesmo nodo com a Lua aproximadamente à mesma distância da Terra e na mesma época do ano para conservação da inclinação axial da Terra, bem como a sua distância ao Sol, fator que determina o diâmetro aparente das sombras umbral e penumbral da Terra. A periodicidade e recorrência dos eclipses lunares, baseados na harmonia entre três períodos orbitais da Lua, são governadas pelo chamado período de Saros. Quaisquer dois eclipses separados por um período de Saros compartilham características semelhantes. Um Saros corresponde a aproximadamente 223 meses sinódicos, ou 239 meses anômalos, ou 242 meses dracônicos, períodos semelhantes, dentro de algumas horas, que correspondem ao valor próximo de 6.585 dias (~18 anos). O fato de o período de Saros não ser igual a um número inteiro de dias, revela que eclipses subsequentes são visíveis de diferentes partes do globo terrestre. Após cada Saros, o eclipse se repete quase nas mesmas condições, porém com, aproximadamente, 8 horas de atraso. São necessários 3 períodos Saros (~54 anos e 34 dias), período denominado de exeligmos, para que os eclipses ocorram praticamente nas mesmas condições (Nasa, 2012).
Matematicamente:
223 meses sinódicos = 6585,3223 dias = 6585d 07h 43m;
239 meses anomalísticos = 6585,5375 dias = 6585d 12h 54m;
242 meses dracônicos = 6585,3575 dias = 6585d 08h 35m
*d = dias, h = horas e m = minutos
Metodologia
Na Figura 3, é apresentada uma representação do alinhamento Sol-Terra-Lua durante um eclipse lunar total, bem como um diagrama correlacionando o raio do Sol (RSol), da Terra (RTerra) e do cone de sombra da umbra (RUmbra), e as distâncias entre o Sol e a Terra (dSol-Terra) e entre a Terra e a Lua (dTerra-Lua). Pela diferença entre os raios do Sol e da Terra (RSol – RTerra), e entre os raios da Terra e da umbra (RTerra – RUmbra), obtemos dois triângulos retângulos congruentes, com lados proporcionais, o que nos permite escrever a seguinte equação:
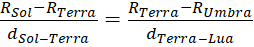 (1),
(1),
que, resolvendo para o raio da umbra,
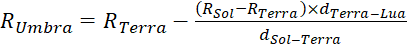 (2).
(2).
Dessa forma, conhecendo os valores dos raios R do Sol e da Terra, bem como as distâncias entre os astros, aplicando os valores na equação (2), podemos determinar o valor aproximado do raio da umbra. O valor do raio do Sol pode ser obtido em um experimento simples com o uso de uma câmara escura de orifício, utilizada para fazer a projeção da imagem do Sol sobre um anteparo e determinar seu diâmetro angular e, por conseguinte, seu diâmetro absoluto (ORTIZ, 2011). A distância média Sol-Terra é comumente obtida pelo registro de fenômenos de trânsito planetário (Vênus e Mercúrio) em frente ao Sol, conforme demonstrado por Martins (2021). Bruning (1991) descreve uma metodologia didática de como determinar a distância Terra-Lua através do registro de um eclipse lunar. Didaticamente, a reprodução do conhecido Experimento de Eratóstenes (Ellinogermaniki, 2021), que consiste em medir o ângulo de incidência dos raios solares em dois pontos separados ao longo do mesmo meridiano, em determinadas épocas do ano e, determinando-se a diferença entre estes ângulos e a distância entre os pontos, permite estimar o valor de RTerra.
Neste trabalho, a fim de obtermos um resultado com melhor precisão, utilizamos valores padrões aplicados na equação (2), na determinação do valor de RUmbra. Os valores de RSol = 6,957 x 108 m e RTerra = 6,378 x 106 m são considerados constantes de conversão nominais conforme definição da União Astronômica Internacional (IAU do inglês: International Astronomical Union) (MAMAJEK, 2015). Para dSol-Terra utilizamos o valor de 1,496 x 1011 ± 3 m (LUZUM, 2011) que se refere à determinação do valor da Unidade Astronômica (UA), uma unidade de comprimento que equivale, aproximadamente, à distância média Sol-Terra. Medidas utilizando técnicas de radar (FISCHER, 1962) permitiram determinar a distância média até a Lua como sendo dTerra-Lua = (384.403 ± 2) x 103 m. Aplicando os valores anteriormente descritos, encontramos o valor aproximado para o raio do cone de sombra da umbra:
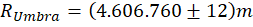
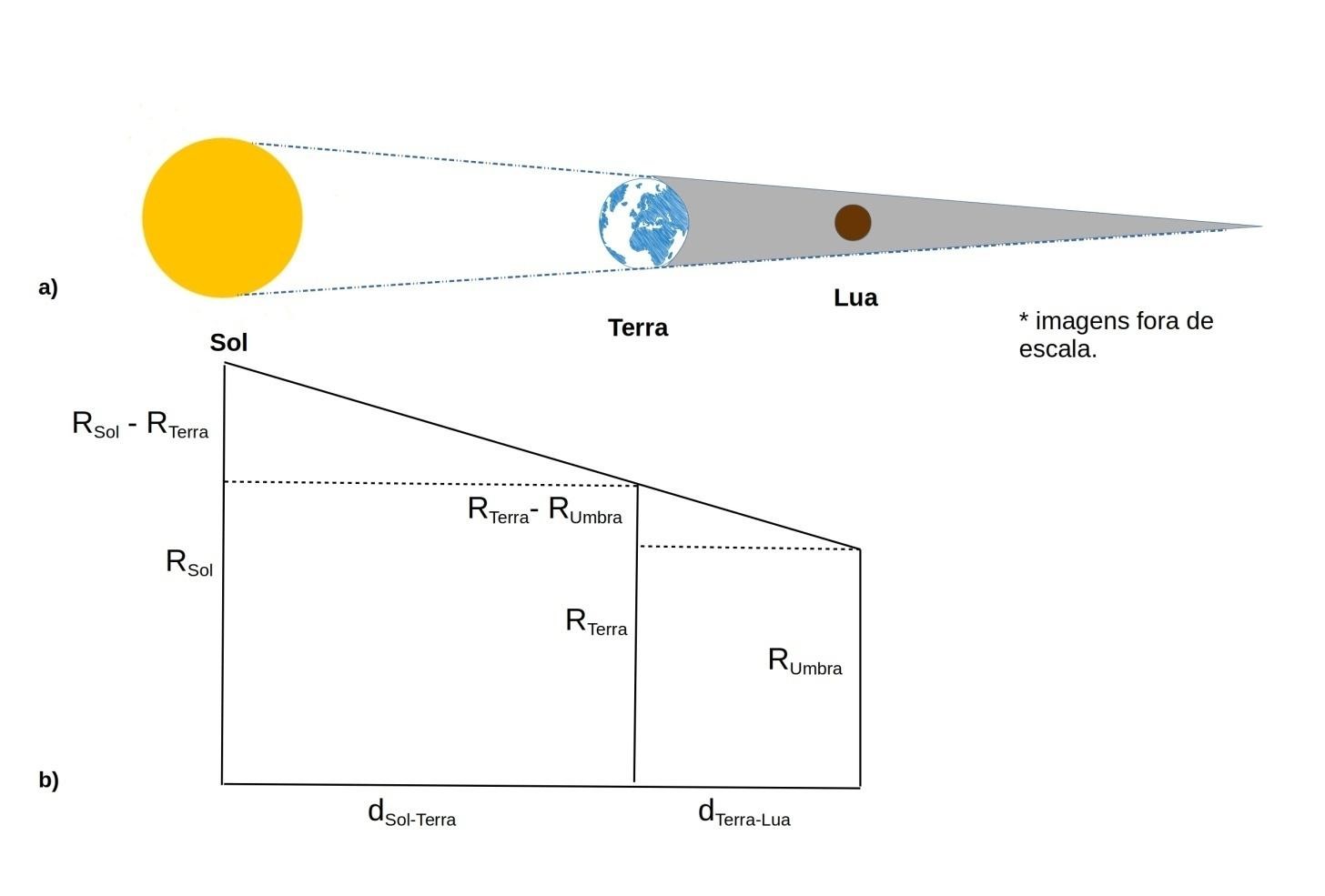
Figura 3: a) Representação de um alinhamento Sol-Terra-Lua durante um eclipse lunar total, com o respectivo cone de sombra da umbra. b) Diagrama esquemático correlacionando os raios R do Sol, da Terra e do cone de sombra da umbra, bem como as distâncias entre os astros
Pela análise da sobreposição de fotografias de um eclipse lunar total, podemos mensurar o valor do raio da Lua por comparação com o valor obtido de RUmbra.
Resultados experimentais
Na Figura 4, é apresentado um mosaico circular de fotografias obtidas durante o eclipse lunar total ocorrido em 21 de janeiro de 2019. Este eclipse foi registrado como um eclipse lunar onde o caminho de trânsito da Lua não atravessou o centro da umbra (ver Figura 5). A imagem é composta por 12 exposições únicas obtidas com o uso de uma câmera modelo Canon EOS 600D, acoplada a um telescópio modelo Meade ETX 90 (distância focal de 1250 mm), com intervalo de exposição de 4 segundos em, aproximadamente, 10 minutos de intervalo. A imagem foi estruturada pelo encaixe da sombra da curvatura da Terra, de cada fotografia, de modo a permitir uma visualização representativa do círculo do cone da umbra. Utilizando-se do software Adobe Photoshop, cada fotografia foi mesclada no modo de mesclagem de uma camada, para criar a visão de transparência com todas as luas.

Figura 4: Mosaico circular de astrofotografias do eclipse lunar total ocorrido em 21 de janeiro de 2019. É possível identificar a representação do círculo do cone de sombra (umbra) projetado pela Terra durante um eclipse lunar
Com o uso de um software de edição e manipulação de imagens (GIMP) medimos, na imagem da Figura 4, o valor dos Raios da Lua (RLua) e da umbra (RUmbra) em pixel várias vezes para a obtenção de um valor médio. Por definição, “pixel” é o menor componente de uma imagem digital. As medidas revelam que o diâmetro da umbra representa, aproximadamente, 2,4 vezes o diâmetro lunar. O valor de RLua, em metros, é obtido usando uma simples "regra de três", conforme a equação (3):
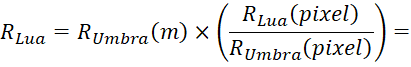
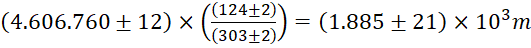 (3)
(3)
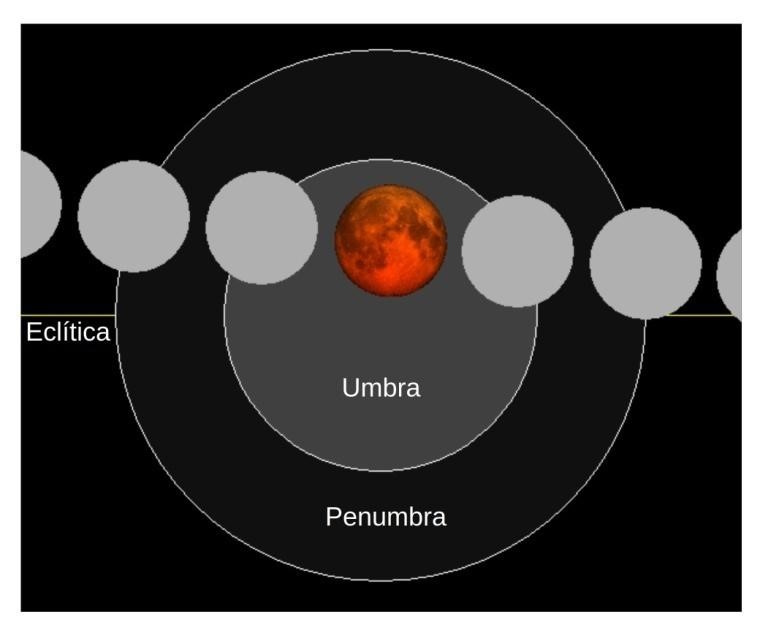
Figura 5: Caminho de trânsito da Lua através da penumbra/umbra da Terra durante o eclipse lunar total ocorrido em 21 de janeiro de 2019
Fonte: https://en.wikipedia.org/wiki/January_2019_lunar_eclipse, acesso em 28 de abril de 2021.
Conclusão
Considerando que a técnica apresentada neste trabalho permitiu determinar o valor do raio da Lua com boa aproximação ao valor padrão atualmente aceito (1.738 x 103 m) (Williams, 2010), concluímos que um valor correspondente, considerando a margem de incerteza do valor calculado neste trabalho, poderá ser reproduzido por educadores junto a estudantes da última fase da Educação Básica.
Referências
BATTEN, A. H. Aristarchus of Samos. Journal of the Royal Astronomical Society of Canada, Toronto, v. 75, nº 1, 1981.
BIRRIEL, J. J.; ADKINS, J. K. Estimating the size of Earth's umbral shadow using sky brightness light curves during a lunar eclipse. American Journal of Physics, College Park, v. 87, nº 12, p. 994-996, set. 2019.
BISHOP, R. L. Observer's handbook 1991. Toronto: The Royal Astronomical Society of Canada, 1991.
BRUNING, D. H. Determining the Earth–Moon distance. American Journal of Physics, College Park, v. 59, nº 9, p. 850, set. 1991.
CHALUB, F. A. C. C. The Saros cycle: obtaining eclipse periodicity from Newton’s laws. Revista Brasileira de Ensino de Física, São Paulo, v. 31, nº 1, p. 1303.1-1303.6, abr. 2009.
ELLINOGERMANIKI AGOGI. The Eratosthenes Experiment. Disponível em: https://eratosthenes.ea.gr. Acesso em: 10 maio 2021.
FISCHER, I. Parallax of the Moon in terms of a world geodetic system. The Astronomical Journal, Bristol, v. 67, nº 6, p. 373-378, ago. 1962.
LUZUM, B. et al. The IAU 2009 system of astronomical constants: the report of the IAU working group on numerical standards for fundamental Astronomy. Celestial Mechanics and Dynamical Astronomy, v. 110, nº 4, p. 293-304, jul. 2011.
MAMAJEK, E. E. et al. IAU 2015 Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties. arXiv e-prints, Nova York, v. 1, out. 2015. Disponível em: https://arxiv.org/abs/1510.07674. Acesso em: 10 maio 2021.
MARTINS, A. et al. Cálculo do valor da unidade astronômica: como o trânsito de Mercúrio nos indica a nossa distância ao Sol. Revista Latino-Americana de Educação em Astronomia, São Carlos, nº 30, p. 51-64, jan. 2021.
NATIONAL AERONAUTICS AND SPACE ADMINISTRATION (NASA). Eclipses and the Moon's Orbit, 2012. Disponível em: https://eclipse.gsfc.nasa.gov/SEhelp/moonorbit.html. Acesso em: 10 maio 2021.
______. Visual appearance of lunar eclipses. 2009. Disponível em: https://eclipse.gsfc.nasa.gov/ LEcat5/appearance.html. Acesso em: 10 maio 2021.
______. Periodicity of Lunar Eclipses. 2012. Disponível em: https://eclipse.gsfc.nasa.gov/ LEsaros/LEperiodicity.html#1. Acesso em: 10 maio 2021.
ORTIZ, R. Experimentos de Astronomia para o Ensino Fundamental e Médio, 2ª ed. 2011. Disponível em: http://each.uspnet.usp.br/ortiz/classes/experimentos_2011.pdf. Acesso em: 10 maio 2021.
SILVA, R. S. The Astrophotography as Aid for Astronomy Education. Research & Reviews: Journal of Educational Studies, Hyderabad, v. 2, nº 2, p. 10-12, abr. 2016.
SILVEIRA, F. L. As variações dos intervalos de tempo entre as fases principais da Lua. Revista Brasileira de Ensino de Física, São Paulo, v. 23, nº 3, p. 300-307, set. 2001.
WILLIAMS, D. R. Moon Fact Sheet. 2010. Disponível em: https://web.archive.org/web/20100323165650/ http://nssdc.gsfc.nasa.gov/ planetary/factsheet/moonfact.html. Acesso em: 10 maio 2021.
Agradecimentos
Os autores deste trabalho agradecem ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) pelo apoio financeiro na compra de equipamentos e bolsas de estudo a estudantes universitários.
Publicado em 26 de outubro de 2021
Como citar este artigo (ABNT)
MARTINS, Alessandro. Medindo o tamanho da Lua pela observação de um eclipse lunar. Revista Educação Pública, v. 21, nº 39, 26 de outubro de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/39/medindo-o-tamanho-da-lua-pela-observacao-de-um-eclipse-lunar
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

