Uma proposta de atividade de resolução de problema para a Educação no Campo
Cintia Aparecida Bodnar
Especialista no Ensino da Matemática (Unespar – câmpus União da Vitória)
Fabiana Vanessa Busck
Especialista no Ensino da Matemática (Unespar – câmpus União da Vitória)
Ilson Roque Giaretta
Especialista no Ensino da Matemática (Unespar – câmpus União da Vitória)
Eliziane Ribeiro
Mestra em Ensino de Ciência e Tecnologia (UTFPR – câmpus Ponta Grossa)
As Diretrizes Curriculares da Educação do Campo pontuam que
a Educação do Campo é uma política pública que nos últimos anos vem se concretizando no estado do Paraná, assim como no Brasil. Uma política pública pensada, mediante a ação conjunta de governo e sociedade civil organizada. Caracterizada como o resgate de uma dívida histórica do Estado aos sujeitos do campo, que tiveram negado o direito a uma Educação de qualidade, uma vez que os modelos pedagógicos ora marginalizavam os sujeitos do campo, ora vinculavam-se ao mundo urbano, ignorando a diversidade sociocultural do povo brasileiro, especialmente aquela expressa na prática social dos diversos sujeitos do campo (Paraná, 2006, p. 9).
Sabe-se também que, atualmente, a função da escola não é somente formar seus alunos, mas também prepará-los para viver em sociedade, permitindo que tornem-se seres críticos e ativos.
D' Ambrosio (1999, p. 99) define a Educação “como o conjunto de estratégias desenvolvidas pela sociedade para (i) possibilitar a cada indivíduo atingir seu potencial criativo; (ii) estimular e facilitar a ação comum, com a finalidade de viver em sociedade e exercer a cidadania”.
Baseando-se nos aspectos delineados, este estudo tem como objetivo apresentar uma proposta de atividade direcionada para Educação do Campo como forma de introduzir o conteúdo função do 1º grau, utilizando a metodologia de resolução de problemas.
Educação do Campo
A Educação do Campo é constituída de uma história de luta pela Educação dentro dos acampamentos e assentamentos em nosso país. De acordo com Caldart (1990, p. 11), “pais, professores e alunos estão construindo nestes locais uma escola “diferente”, uma escola orgânica à sua organização e aos processos de desenvolvimento rural propostos e implementados pela luta”.
Ressalta-se que essa luta é formada por vários brasileiros, como pontua o documento Por uma Educação do Campo: Declaração 2002, onde consta que
no campo existem milhões de brasileiras e brasileiros [...] que vivem e trabalham no campo, como: pequenos agricultores, quilombolas, povos indígenas, pescadores, camponeses, assentados, reassentados, ribeirinhos, povos da floresta, caipiras, lavradores, roceiros, sem-terra, agregados, caboclos, meeiros, boias-frias, entre outros (Kolling; Cerioli; Caldart, 2002, p. 11).
Assim, pontua-se que, desde o início, o movimento da Educação do Campo decidiu
utilizar a expressão campo, e não o mais usual meio rural, como objetivo de incluir [...] uma reflexão sobre o sentido atual do trabalho camponês e das lutas sociais e culturais dos grupos que vivem hoje e tentam garantir a sobrevivência desse trabalho. Mas quando discutimos a Educação do Campo estamos tratando da Educação que se volta ao conjunto dos trabalhadores e das trabalhadoras do campo, sejam os camponeses, incluindo os quilombolas, sejam as nações indígenas, sejam os diversos tipos de assalariados vinculados à vida e ao trabalho no meio rural (Fernandes; Cerioli; Caldart, 1998, p. 9).
A luta por uma Educação de qualidade que respeite a identidade dos habitantes do campo, acima de tudo considerando sua realidade, social, política e sua existência e importância no campo, onde a
diversidade de coletivos humanos apresenta formas específicas de produção de saberes, conhecimentos, ciência, tecnologias, valores, culturas... A Educação desses diferentes grupos tem especificidades que devem ser respeitadas e incorporadas nas políticas públicas e no projeto político pedagógico da Educação do Campo, como por exemplo, a pedagogia da alternância (II Conferência Nacional por uma Educação do Campo, 2004, p. 5-6).
Faz-se necessário citar que, no documento básico do MST – Movimento dos Trabalhadores Rurais Sem Terra – a prática de Educação nas escolas de assentamentos/acampamentos deve seguir os seguintes princípios:
- ter trabalho e organização coletiva como valores fundamentais;
- integrar a escola na organização do assentamento;
- formação integral e sadia personalidade da criança;
- a prática da democracia como parte essencial do processo educativo;
- o professor deve ser sujeito integrado na organização e interesses do assentamento;
- a escola e a Educação devem construir um projeto alternativo de vida social;
- uma metodologia baseada na concepção dialética do conhecimento (Paraná, 2005, p. 29).
Nesse caminhar pelos direitos de Educação nas escolas localizadas na zona rural, várias experiências são utilizadas para construir um novo pensar sobre o que é uma escola do campo, partindo do pressuposto que é
uma escola onde se educa partindo da realidade; uma escola onde o professor e aluno são companheiros e trabalham juntos – aprendendo e ensinando; uma escola que se organiza criando oportunidades para que as crianças se desenvolvam em todos os sentidos; uma escola que incentiva e fortalece os valores do trabalho da solidariedade, do companheirismo, da responsabilidade e do amor à causa do povo. Uma escola que tem como objetivo um novo homem e uma nova mulher, para uma nova sociedade e um novo mundo (Paraná, 2005, p. 31).
O MST aponta como uma escola de assentamento deve ser (Paraná, 2005, p. 39-40):
- deve preparar as crianças para o trabalho no meio rural;
- deve capacitar para a cooperação;
- deve ser coletiva e democrática;
- deve refletir e qualificar as experiências de trabalho produtivo das crianças no assentamento;
- deve ajudar no desenvolvimento cultural dos assentados;
- o ensino deve partir da prática e levar ao conhecimento científico da realidade;
- o coletivo deve se preocupar com o desenvolvimento pessoal de cada aluno;
- o professor tem que ser militante;
- deve ajudar a formar militantes e exercitar a mística da luta popular;
- é lugar de viver e refletir sobre uma nova ética.
A partir disso, o ensino na visão do MST não parte do conteúdo, e sim a partir da prática. Ela deve partir da experiência que o estudante possui, seja está à experiência do trabalho, de organização, do relacionamento com os outros.
Sobre as propostas pedagógicas das Diretrizes Operacionais para a Educação Básica nas Escolas do Campo, registra-se a possibilidade de elaboração de:
propostas pedagógicas que valorizem, na organização do ensino, a diversidade cultural e os processos de interação e transformação do campo, a gestão democrática, o acesso do avanço científico e tecnológico e respectivas contribuições para a melhoria das condições de vida e a fidelidade aos princípios éticos que norteiam a convivência solidária e colaborativa nas sociedades democráticas (Brasil, 2001, p. 25).
As diretrizes para a Educação do Campo se encaminham no sentido de propor o ensino e a aprendizagem por meio de atividades que levam de encontro a situações reais, práticas, onde o conhecimento ensinado possa ser observado e utilizado em atividades presentes no cotidiano dos alunos, assim, transformando o aluno em um cidadão participativo da sociedade em que está inserido.
O ensino da Matemática
Acredita-se que o papel da Educação Matemática seja proporcionar aos alunos um ambiente de aprendizagem interessante e significativo, que os prepare para uma sociedade que exige indivíduos críticos, capazes de argumentar e de tomar decisões em situações diversas encontradas no dia a dia.
Percebe-se que ao se estabelecerem parâmetros para o ensino da Matemática, pretende-se dar ênfase às necessidades do desenvolvimento dos alunos, com diferentes motivações, interesses e capacidades. Tendo em vista a sua inserção em um mundo de constantes mudanças e contribuindo para o desenvolvimento das capacidades que serão deles exigidas em sua vida social e profissional, os Parâmetros Curriculares Nacionais do Ensino Médio: Ciência da Natureza, Matemática e suas tecnologias (PCNEM) sugerem que,
em um mundo onde as necessidades sociais, culturais e profissionais ganham novos contornos, todas as áreas requerem alguma competência em Matemática e a possibilidade de compreender conceitos e procedimentos matemáticos são necessários tanto para tirar conclusões e fazer argumentações, quanto para o cidadão agir como consumidor prudente ou tomar decisões em sua vida pessoal e profissional (PCNEM, 1999, p. 40).
Essas mudanças também se refletem nas salas de aula. Torna-se cada vez mais difícil despertar a atenção dos alunos, os quais vivem numa sociedade amplamente tecnológica e competitiva. É evidente o desinteresse dos alunos nas aulas cuja metodologia se baseia apenas na forma oral e o seu único recurso é o quadro e o giz. Na disciplina de Matemática, é comum encontrar professores que não relacionam o conteúdo com a realidade vivenciada dos alunos, deixando os alunos desinteressados.
De acordo com Siqueira (2007, p. 10),
percebendo a grande importância do professor na sala de aula, educadores e matemáticos deram novos passos para a criação de metodologias de forma a motivar o ensino da Matemática, uma vez que a metodologia tradicional não respondia mais às expectativas dos alunos, de um mundo em mudança, e da forma bancária de ensino. Os meios de comunicação, nos anos de 1980, passaram a exigir mudanças e, com o decorrer dos anos, intensificaram-se cada vez mais, principalmente com o uso da tecnologia.
Nesse sentido, questiona-se que para ser professor de Matemática não basta apenas saber muita Matemática, deve-se ter o conhecimento de como exercer o papel de educador. O professor e o aluno devem trocar experiências e ideias vivenciadas na sociedade, na escola, acerca da Matemática, de seu ensino e aprendizagem.
Tendências da Educação Matemática
A área da Educação tem sido alvo de constantes pesquisas que buscam inovar e ampliar o ensino. Isso faz com que haja o desenvolvimento das práticas pedagógicas de vários professores que procuram amenizar as barreiras da aprendizagem.
As aulas tradicionais consistem em aulas expositivas. O professor parte de uma definição, demonstra a fórmula e, em seguida, são realizados vários exercícios de mecanização. Muitas vezes, a repetição de vários exercícios disfarça a compreensão por parte dos alunos, pois, eles acabam memorizando o passo a passo, sem compreender.
Segundo Micotti (1999), o ensino tradicional acaba acentuando a transmissão do saber já construído pelo professor e a aprendizagem passa a ser vista como uma impressão na mente dos alunos.
Muitos autores do campo da Educação Matemática evidenciam a necessidade de se adequar o trabalho escolar às novas tendências. Tendo em vista que a metodologia tradicional não mais respondia às expectativas dos alunos, mesmo sendo para muitos a forma mais cômoda.
De acordo com Siqueira (2007, p.10):
o ensino da Matemática na forma tradicional passou por modificações na busca do que é o melhor para os alunos e para os profissionais em Educação. De forma que a linha tradicional não se apresenta como a de melhor aceitação pelos alunos da sociedade atual, mesmo sendo a mais cômoda e mais segura para aqueles que assumem o papel de difusor dessa parte do conhecimento.
Existem hoje cinco tendências aceitas para o ensino e aprendizagem em Matemática, que proporcionam aos alunos um ambiente mais ativo e estimulante. Essas tendências são: a Etnomatemática, a História da Matemática, a Matemática Crítica, a Modelagem Matemática e a Resolução de Problemas.
Os conteúdos, portanto, podem transitar por todas as tendências da Educação matemática. A Figura 1 sugere que tais tendências se articulem com enfoques nos conteúdos matemáticos.
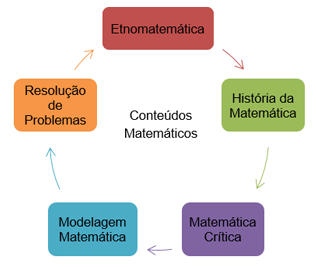
Figura 1: As tendências da Educação Matemática
Desse modo, observam-se a preocupação de vários professores na busca por melhorias para o ensino, que respondam às expectativas da comunidade escolar. Acredita-se que não existe um único caminho de ensinar, mas ao ampliar as possibilidades de escolhas, possibilita-se aos estudantes uma aprendizagem mais significativa.
A metodologia de Resolução de Problemas, geralmente desenvolvida através de situações problemas que visam à construção de um novo conceito, relacionando a Matemática com situações cotidianas, que despertem o interesse dos estudantes, parece ser um bom caminho.
Resolução de problemas na Educação Matemática
A Matemática é uma das ciências mais belas e presentes na vida do ser humano. Atualmente, há uma enorme preocupação em como ensiná-la de forma que o aluno obtenha o melhor aproveitamento.
De acordo com Onuchic (1999), estudos na área da Educação foram realizados com o objetivo de se obter maneiras diversificadas de ensinar. Durante o século XX, a Educação matemática passou por reformas. Estas reformas possibilitaram o surgimento de novas metodologias de ensino, que auxiliam o professor na sua prática pedagógica, oportunizando aos alunos uma aprendizagem mais significativa.
A Matemática tem despertado um papel importante no desenvolvimento da sociedade, onde os Problemas de Matemática têm ocupado um papel central no currículo escolar desde a Antiguidade. Mas, somente na década de 70, tiveram início as investigações sistemáticas sobre a Resolução de Problemas e implicações curriculares.
A importância dada à Resolução de Problemas é, portanto, recente e somente nessa década é que os educadores matemáticos passaram a aceitar a ideia de que o desenvolvimento da capacidade de resolver problemas merecia mais atenção. A caracterização da Educação Matemática, em termos de Resolução de Problemas, reflete uma tendência de reação a caracterização passadas, que configuram com um conhecimento a ser obtido por rotina ou por exercício mental. No fim dos anos 70, a Resolução de Problemas emerge, ganhando espaço no mundo inteiro (Onuchic; Allevato, 2004, p. 215).
Destaca-se que a Resolução de Problemas é uma das grandes tendências da Educação matemática. Mas antes de descrever sobre a Resolução de Problemas, é importante saber identificar um problema.
Medeiros (2007, p. 37) destaca a diferença entre problemas e exercícios:
Problemas não são chamados de problemas se o resolvedor não necessita identificar situações matemáticas, ou seja, se ele pode resolver o problema utilizando um simples modelo de resolução de um problema já resolvido. Tais problemas são meros exercícios, já que podem ser numerosos e envolve um único conteúdo e uma única metodologia.
A Resolução de Problemas é uma importante contribuição para o processo de ensino e aprendizagem, permitindo que o professor possibilite ao aluno a capacidade de desenvolver seu pensamento matemático. Já a aprendizagem através da forma mecânica (repetição) é adquirida uma vez e esquecida rapidamente, se não houver uma revisão. Na aprendizagem por meio da Resolução de Problemas, os conceitos consistem na relação de conhecimentos anteriores, proporcionando a compreensão de maneira gradativa.
Uma pessoa adquire um conceito quando é capaz de dotar de significados um material ou uma informação que lhe é apresentada, ou seja, quando “compreende” esse material, em que compreende seria equivalente, mais ou menos, traduz algo com suas próprias palavras (Pozo, 2000, p. 25).
Por esse motivo, a Resolução de Problemas se identifica como um meio viável do professor utilizar em suas aulas. Os alunos constroem seus conceitos com base nos que já possuem e, gradativamente, o professor pode explorá-los didaticamente, aprimorando-os. Introduzir um novo conteúdo pelo viés da Resolução de Problemas possibilita incentivar o aluno a interagir com os conhecimentos matemáticos, estabelecendo conexões entre o conhecimento prévio e os novos conhecimentos.
Ainda relatando a importância de se trabalhar a Matemática através de situações problemas, vale citar Onuchic (1999, p. 207), que considera de grande importância a Resolução de Problemas, principalmente ao se introduzir um novo tópico dos conteúdos matemáticos em sala de aula:
Podemos começar um tópico matemático com uma situação-problema que expressa aspectos-chave desse tópico são desenvolvidas técnicas matemáticas como respostas razoáveis para problemas. […] O aprendizado, deste modo, pode ser visto como um movimento concreto (um problema do mundo real que serve como exemplos do conceito ou técnicas operatórias) para o abstrato (uma representação simbólica de uma classe de problemas e técnicas para operar com esses símbolos) (Onuchic, 1999, p. 207).
As estratégias que os alunos utilizam para resolver os problemas podem tornar as aulas mais motivadoras e desafiadoras. A Resolução de Problemas promove ao aluno o desenvolvimento do raciocínio e criatividade, sua capacidade crítica e matemática, onde se envolve ativamente no processo de sua aprendizagem, o possibilitando aprender a lidar e a encontrar soluções novas com questões da Matemática e também fora do âmbito escolar.
É possível por meio da resolução de problemas desenvolverem no aluno iniciativa, espírito explorador, criatividade, independência e a habilidade de elaborar um raciocínio lógico e fazer uso da inteligente e eficaz dos recursos disponíveis, para que ele possa propor boas soluções às questões que surgem em seu dia a dia, na escola e fora dela (Dante apud Souza, s/d, p. 3).
De acordo com essa tendência, o mais importante é o prazer que os alunos têm em resolver problemas. Para muitos, o problema com maior grau de dificuldade é aquele que proporciona maior satisfação após ser resolvido.
Butts (1997, p. 54) afirma que “o verdadeiro prazer em estudar Matemática é o sentimento de alegria que vem da resolução de problemas quanto mais difícil o problema, maior a satisfação”.
O ensino através da Resolução de Problemas é visto como uma metodologia adequada, que permite ao aluno exercer o papel central durante as aulas de Matemática, incentivando-o a tomar decisões.
A Resolução de Problemas é peça central para o ensino de Matemática, pois o pensar e o fazer se mobilizam e se desenvolvem quando o individuo está engajado ativamente no enfrentamento de desafios. Esta competência não se desenvolve quando propomos apenas exercícios de aplicação de conceitos técnicas matemáticos, pois, neste caso o que está em ação é a simples transposição analógica: o aluno busca na memória um exercício semelhante e desenvolve passos análogos aos daquela situação, o que não garante que seja capaz de utilizar seus conhecimentos em situações diferentes ou mais complexas (Brasil, 1998, p. 154).
Acredita-se que a Resolução de Problemas consiste em um processo de aprendizagem em que os alunos constroem conceitos, descobrem relações, observam, experimentam, argumentam, conjecturam e avaliam.
A essência da Matemática está em resolver problemas, e aprender a resolvê-los é um dos motivos para ensinar e aprender Matemática. Mas, para isso, os alunos devem ser confrontados com vários tipos de problemas para que se familiarizem com diferentes estratégias de resolução.
Uma sugestão metodológica para o ensino de função do 1º grau
Uma sugestão metodológica para introduzir o estudo do conceito de função do 1º grau se encaminha no sentido de descrever uma atividade de Resolução de Problemas. Por exemplo, levar a calcular a relação de custo-benefício para o agricultor entre comprar um trator novo, um trator usado ou contratar um serviço terceirizado.
A atividade desenvolvida refere-se ao trator, mais especificamente o trator Valtra 785, que antes era conhecido pelo nome de Valmet 785, que é um dos tratores mais utilizados na região de Bituruna pelos pequenos agricultores.
Inicialmente, o trator foi um substituto da força animal; hoje em dia, é projetado para múltiplos usos, entre eles, acionamento de outras máquinas, transporte, irrigação, tração e sistemas remotos de controle hidráulico, entre outros. Dessa forma, com a utilização de tratores nas suas atividades diárias, o agricultor aumenta a sua produtividade e melhora a qualidade das operações agrícolas. A agricultura familiar é considerada uma atividade econômica fundamental para o desenvolvimento socioeconômico sustentável no meio rural.
Alguns agricultores têm dificuldade em escolher a melhor opção quando se trata da utilização de um trator que leva em consideração a relação custo-benefício. Pensando neste problema, o objetivo deste trabalho é encontrar qual a opção que representa o melhor custo-benefício para o agricultor em relação às horas trabalhadas durante o ano em suas atividades agrícolas: um trator novo Valtra 785, um trator usado Valtra 785 ou serviço terceirizado.
Com o programa Mais Alimentos, do Governo Federal, que tem como intuito de equipar e fortalecer a agricultura familiar brasileira e se contrapor à crise alimentar mundial, o pequeno agricultor tem meios para comprar um trator novo. É um plano com o objetivo de incentivo à mecanização massiva, de financiamento de tratores e máquinas para pequenos agricultores, promovendo a geração de renda no campo e o aumento da produção de alimentos para o consumo. Podendo ser financiado até R$ 100 mil por família de agricultores, com juros de 2% ao ano, com dez anos de prazo para pagamento para compra de máquinas e equipamentos. Atende dez culturas agrícolas e outras atividades, como pecuária, avicultura e pesca.
Os tratores usados também são financiados pelo Governo Federal, pelo Programa Nacional de Fortalecimento da Agricultura Familiar – Pronaf Investimento, financiando tratores usados a partir de R$ 30 mil a R$ 50 mil por família de agricultores, com juro de 4% ao ano, tendo em vista oito anos de prazo para pagamento.
Visando determinar um problema que encontre a opção que representa melhor o custo-benefício para o agricultor que utiliza um trator para o exercício de suas atividades agrícolas, utilizaremos os seguintes dados coletados:
- Trator novo Valtra 785, R$ 70.000,00 financiado pelo Mais Alimento.
- Trator usado Valtra 785 revisado, R$ 39.000,00 financiado pelo Pronaf – Investimento.
- Serviço terceirizado por hora, R$ 60,00.
Com as informações obtidas, temos a Tabela 1, que mostra o custo de um trator Valtra 785 por ano, com os valores das parcelas anuais com juro.
Tabela 1: Custo do trator novo
Tempo (anos) |
Trator Valtra 785 novo 70 mil |
Valor da parcela anual fixa |
Juro fixo de 2% ao ano |
Valor da parcela anual + juro |
1 |
70.000,00 |
7.000,00 |
1.400,00 |
8.400,00 |
2 |
63.000,00 |
7.000,00 |
1.260,00 |
8.260,00 |
3 |
56.000,00 |
7.000,00 |
1.120,00 |
8.120,00 |
4 |
49.000,00 |
7.000,00 |
980,00 |
7.980,00 |
5 |
42.000,00 |
7.000,00 |
840,00 |
7.840,00 |
6 |
35.000,00 |
7.000,00 |
700,00 |
7.700,00 |
7 |
28.000,00 |
7.000,00 |
560,00 |
7.560,00 |
8 |
21.000,00 |
7.000,00 |
420,00 |
7.420,00 |
9 |
14.000,00 |
7.000,00 |
280,00 |
7.280,00 |
10 |
7.000,00 |
7.000,00 |
140,00 |
7.140,00 |
Na Tabela 2, apresentamos o custo de um trator usado Valtra 785 por ano, com os valores das parcelas anuais com juro.
Tabela 2: Custo do trator usado com os valores das parcelas
Tempo (anos) |
Trator Valtra 785 usado 39 mil |
Valor da parcela anual fixa |
Juro fixo de 4% ao ano |
Valor da parcela anual + juro |
1 |
39.000,00 |
4.875,00 |
1.560,00 |
6.435,00 |
2 |
34.125,00 |
4.875,00 |
1.365,00 |
6.240,00 |
3 |
29.250,00 |
4.875,00 |
1.170,00 |
6.045,00 |
4 |
24.375,00 |
4.875,00 |
975,00 |
5.850,00 |
5 |
19.500,00 |
4.875,00 |
780,00 |
5.655,00 |
6 |
14.625,00 |
4.875,00 |
585,00 |
5.460,00 |
7 |
9.750,00 |
4.875,00 |
390,00 |
5.265,00 |
8 |
4.875,00 |
4.875,00 |
195,00 |
5.070,00 |
Os tratores possuem alguns gastos para sua utilização. São os seguintes:
Custo por hora trabalhada do trator novo Valtra 785:
- óleo diesel, R$ 10,00;
- óleo lubrificante, hidráulico, graxa, R$ 2,00.
Custo por hora trabalhada do trator usado Valtra 785:
- óleo diesel, R$ 10,00;
- óleo lubrificante, hidráulico, graxa, R$ 2,00;
- manutenção mecânica, R$ 3,00.
Seguindo estas informações, temos que, com a compra do trator novo ou usado teremos uma parcela anual e mais os custos por hora trabalhada e o serviço terceirizado tem um preço fixo por hora. Observamos que o custo depende das horas trabalhadas do trator. A partir desta hipótese, selecionamos as variáveis:
c(h): custo por hora trabalhada do trator
h: hora trabalhada do trator por ano
Após selecionarmos as variáveis, o passo seguinte da atividade de modelagem é a formulação do modelo matemático.
Com os dados da Tabela 1, fazemos uma média aritmética das parcelas anuais do trator novo para saber qual será o valor a ser pago em cada ano pelo trator novo, assim temos:
M = 77.700,00/10= 7.770,00
Com os dados da Tabela 2, realizamos uma média aritmética das parcelas do trator usado; logo:
M = 46.020,00/8 = 5.752,50
Calculando o total do custo por hora trabalhada do trator, temos:
- Trator novo, R$ 12,00;
- Trator usado, R$ 15,00.
Utilizando a hipótese de que o custo depende das horas trabalhadas do trator, temos mais a parcela anual do trator quando se trata da sua compra, desenvolvemos os nossos modelos:
Para o trator novo Valtra 785:
c(h) = 12,00h + 7.770,00
Para o trator usado Valtra 785:
c(h) = 15,00h + 5.752,50
Quando utilizado o serviço terceirizado:
c(h) = 60,00/h
Quando calculamos o valor do trator por horas durante o período de um ano, sua representação gráfica pode ser a seguinte:
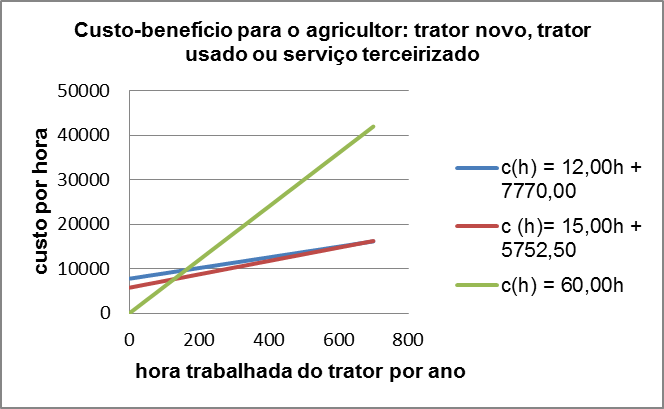
Figura 2: Cálculo do custo-benefício para o agricultor: trator novo, trator usado ou serviço terceirizado
A partir da representação gráfica dos modelos, podemos observar que o agricultor que utiliza aproximadamente mais de 127 horas trabalhadas com o trator do serviço terceirizado fica inviável pelo custo que se torna muito alto. Mas para o agricultor que utiliza mais de 670 horas, a compra de um trator novo se torna viável. Agora, para aquele agricultor que fica entre essa faixa de horas é aconselhado a compra de um trator usado.
Considerações finais
Cada vez mais, a sociedade requer pessoas que sejam capazes de apresentar situações inovadoras para os problemas encontrados nos mais diversos contextos em que estejam inseridos. Para atender essas necessidades sociais, a escola também necessita desenvolver em seus alunos tais capacidades.
Com esse intuito, acredita-se que a Resolução de Problemas, enquanto estratégia de ensino e aprendizagem, possibilita uma articulação entre os conteúdos matemáticos com outras áreas do conhecimento, por meio de situações com referência na realidade.
Um dos conteúdos que pode ser trabalhado através da Resolução de Problemas é a função do 1º grau, que possibilita utilizar dados reais, para introduzir esse conceito. Por meio dessa atividade, o aluno pode interferir em sua realidade, ou seja, podendo ajudar a sua família a economizar quando é necessária a utilização de um trator para realizar as suas atividades agrícolas presentes no seu dia a dia. No entanto, cabe ressaltar que nossa proposta enfatiza o uso da Resolução de Problemas para introduzir o conceito de Função do 1º grau, porém não foi desenvolvida em sala de aula.
Acredita-se que este artigo ofereça contribuições para o ensino da Matemática e possa ser indicado como um dos possíveis caminhos para um trabalho diferenciado nas aulas de Matemática nas escolas do campo.
Referências
BUTTS, T. Formulando Problemas Adequadamente. In: KRULIK, S. e REYS, R. E. A Resolução de Problemas na Matemática escolar. São Paulo: Atual, 1997. p. 33-48.
D' AMBRÓSIO, U. A História da Matemática: questões historiográficas e políticas e reflexos na Educação Matemática. In: BICUDO, M. A. V. (Org.). Pesquisa em Educação Matemática: concepções & perspectivas. São Paulo: Editora Unesc, 1999. p. 97 -115.
BRASIL. Ministério da Educação. Conselho Nacional de Educação. Diretrizes operacionais para a Educação Básica nas Escolas do Campo. Brasília, 2001.
BRASIL. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais: Ensino Médio – PCNEM. Brasília: MEC, 1997.
______. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais Mais Ensino Médio: Orientações Complementares aos Parâmetros Curriculares Nacionais – PCN+. Brasília: MEC, 1998.
CALDART, R. S. Nossa luta é nossa escola: a Educação das crianças nos acampamentos e assentamentos. In: Cartilha Fundep/DER/MST-RS. Porto Alegre: Setor de Educação do MST-RS, 1990.
FERNANDES, B. M.; CERIOLLI, P. R.; CALDART, R. S. (Orgs.). Por uma Educação básica do Campo. Texto-Base da Conferência Nacional. Brasília: UnB, 1998.
II CONFERÊNCIA NACIONAL POR UMA EDUCAÇÃO DO CAMPO. Texto-base. Luziânia, 2004.
KOLLING, E. J.; CERIOLI, P. R.; CALDART, R. S. (Orgs.). Educação do Campo: identidade e políticas públicas. Brasília: Articulação Nacional por uma Educação do Campo, 2002. Coleção por uma Educação do Campo, vol. 4.
MEDEIROS JUNIOR, R. J. Resolução de Problemas e ação didática em Matemática no Ensino Fundamental. Dissertação (Mestrado), Universidade Federal do Paraná, Curitiba, 2007.
MICOTTI, M. O. O ensino e as propostas pedagógicas. In: BICUDO, M. V. (Org.). Pesquisas em Educação Matemática: concepções e perspectivas. São Paulo: Editora Unesp, 1999.
ONUCHIC, L. R. Ensino-aprendizagem de Matemática através da Resolução de Problemas. In: BICUDO, M. A. V. (Org.). Pesquisa em Educação Matemática: concepções & perspectivas. São Paulo: Editora Unesc, 1999. p. 199-218.
______; ALLEVATO, N. S. G. Novas reflexões sobre o ensino-aprendizagem de Matemática através da Resolução de Problemas. In: BICUDO, M. A. V., BORBA, M. C. (Orgs.). Educação Matemática: pesquisa em movimento. São Paulo: Cortez, 2004. p. 213-231.
PARANÁ. Secretaria de Estado da Educação. Dossiê MST Escola: documentos e estudos (1990-2001). Curitiba: SEED-PR, 2005.
______. Diretrizes curriculares de matemática para a Educação Básica: Educação do Campo. Curitiba: SEED-PR, 2006.
POZO, I. J. A aprendizagem e o ensino de fatos e conceitos. In: COLL, César (Org.). Psicologia do Ensino. Porto Alegre: Artes Médicas, 2000.
SIQUEIRA, R. N. Tendências da Educação Matemática na formação de professores. Ponta Grossa: Universidade Tecnológica Federal do Paraná, 2007.
SOUZA, A. B. A resolução de problemas como estratégia didática para o ensino da Matemática. s/d. Disponível em: http://www.matematica.ucb.br/sites/000/68/00000024.pdf. Acesso em: 23 dez. 2020.
Publicado em 09 de março de 2021
Como citar este artigo (ABNT)
BODNAR, Cintia Aparecida; BUSCK, Fabiana Vanessa; GIARETTA, Ilson Roque; RIBEIRO, Eliziane. Uma proposta de atividade de resolução de problema para a Educação no Campo. Revista Educação Pública, v. 21, nº 8, 9 de março de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/8/uma-proposta-de-atividade-de-resolucao-de-problema-para-a-educacao-no-campo
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

