Um relato/estudo sobre o uso de atividades investigativas para o ensino de Estatística na Educação Básica
Geisa Abreu Lira Corrêa dos Santos
Professora do Colégio Pedro II - câmpus Engenho Novo II - Rio de Janeiro
Renato de Carvalho Alves
Professor do Colégio Pedro II - câmpus Engenho Novo II - Rio de Janeiro
O conhecimento estatístico é de suma importância para todos. A todo momento nos deparamos com gráficos, tabelas, pesquisas de opinião e informações, e a falta de conhecimento estatístico prévio nos impede de interpretar corretamente as informações ou mesmo interpretá-las. Recomendações para o ensino de Estatística surgiram já em 1998, nos Parâmetros Curriculares Nacionais (PCN) do Ensino Fundamental:
Com relação à Estatística, a finalidade é fazer com que o aluno venha a construir procedimentos para coletar, organizar, comunicar dados, utilizando tabelas, gráficos e representações que aparecem frequentemente em seu dia a dia. Além disso, calcular algumas medidas estatísticas como média, mediana e moda com o objetivo de fornecer novos elementos para interpretar dados estatísticos (Brasil, 1998, p. 52).
Em 2006, os Parâmetros Curriculares Nacionais do Ensino Médio, especificamente o PCN+, listam os seguintes objetivos de ensino para a Estatística:
- Identificar formas adequadas para descrever e representar dados numéricos e informações de natureza social, econômica, política, científico-tecnológica ou abstrata.
- Ler e interpretar dados e informações de caráter estatístico apresentados em diferentes linguagens e representações, na mídia ou em outros textos e meios de comunicação.
- Obter médias e avaliar desvios de conjuntos de dados ou informações de diferentes naturezas.
- Compreender e emitir juízos sobre informações estatísticas de natureza social, econômica, política ou científica apresentadas em textos, notícias, propagandas, censos, pesquisas e outros meios (Brasil, 2006, p. 124).
Além das recomendações sobre o que ensinar, os PCN trazem também diversas sugestões relativas a como trabalhar os conceitos estatísticos com os alunos. Dentre elas podemos destacar a importância de evitar que os conceitos estatísticos sejam estudados de modo artificial, descontextualizados e centrados apenas no uso de fórmulas e no cálculo de medidas resumo e dispersão. Tais recomendações também estão presentes em trabalhos de diversos pesquisadores. De acordo com Castro e Filho (2015, p. 4), “trabalhar com atividades investigativas favorece o envolvimento e o engajamento dos estudantes”. Para Campos e Coutinho (2019, p. 143),
a Educação Estatística preconiza um olhar voltado especialmente para questões envolvidas no processo de ensino-aprendizagem, valorizando um ambiente no qual se destacam a investigação e a reflexão como elementos primordiais para a construção do conhecimento. Assim, de acordo com os preceitos básicos da Educação Estatística, o trabalho em sala de aula para o ensino-aprendizagem eficiente dessa disciplina deve sempre ser pautado por assuntos relevantes, de interesse dos alunos e que façam parte de sua realidade.
Portanto, não só conhecer a Estatística e seus conceitos, como lidar com eles de forma prática, com base em necessidades oriundas da realidade dos alunos, são fatores que podem contribuir para o maior entendimento desses conceitos.
A motivação para a realização deste trabalho surgiu também dos estudos e reflexões propostos pelos professores da disciplina Estatística e Probabilidade, ministrada no âmbito do curso de doutorado em Ensino de Matemática na UFRJ. Tais estudos, combinados com leituras prévias, despertaram nos autores o interesse em trabalhar a Estatística em suas turmas de Educação Básica a partir dessa perspectiva, além de tentar avaliar os alunos de modo diferente.
O ensino da Estatística
Embora a importância da Estatística seja inegável para a formação de cidadãos conscientes e críticos, sua inserção nos currículos da Escola Básica é de uma época relativamente recente: no Brasil, ocorreu em 1997. Tal fato é relatado por Lopes (2010), que, além de trazer essa informação, já menciona a ênfase equivocada em certos aspectos no ensino da Estatística:
A preocupação em inserir a Estatística nos currículos a partir da Educação Básica é relativamente recente. No currículo americano foi incluído a partir de proposta do National Council of Teachers of Mathematics - NCTM, que indicou a introdução do estudo da Estatística em todos os níveis de escolarização. No Brasil, esse conteúdo passou a fazer parte do ensino da Matemática a partir de 1997, com a publicação dos Parâmetros Curriculares Nacionais - PCN (Brasil, 1997). A interpretação de dados e a leitura de gráficos e tabelas são uma parte da Estatística e fazem parte do bloco de Tratamento da Informação do Ensino Fundamental (1º ao 9º ano) ou do bloco de análise de dados do Ensino Médio (Brasil, 1997; 1998; 1999).
Apesar das recomendações de documentos oficiais para a inclusão da Estatística no currículo, a sua abordagem ainda é principiante e insatisfatória, pois a escola tem o hábito de enfatizar os cálculos, as fórmulas e os procedimentos ao invés de explorar situações a partir de contextos reais (Lopes, 2010).
Os pesquisadores Gal e Garfield (1999) propõem várias metas a serem alcançadas para que o ensino da Estatística se dê de modo efetivo, contribuindo para a formação dos estudantes. Essas metas, com as quais concordam também Campos, Wodewotzki e Jacobini (2011, p. 14), são:
- entender o propósito e a lógica das investigações estatísticas;
- entender o processo de investigação estatística;
- dominar as habilidades usadas nos processos de investigação estatística;
- entender as relações matemáticas presentes nos conceitos estatísticos;
- entender a probabilidade, a chance, a incerteza, os modelos e a simulação;
- desenvolver habilidades interpretativas para argumentar, refletir e criticar;
- desenvolver habilidades para se comunicar estatisticamente, usando corretamente a sua terminologia.
Campos, Wodewotzki e Jacobini (2011, p. 14) ainda acrescentam a essas sete metas as três seguintes:
- desenvolver habilidades colaborativas e cooperativas de trabalho em equipe;
- desenvolver habilidades de transposição de saberes escolares para sua vida cotidiana, como cidadão e profissional;
- desenvolver hábitos de questionamento dos valores, grandezas, dados e informações.
Não foi nosso propósito, em um período do ano bem pontual, e apenas com alunos de uma série específica, propor um trabalho que desse conta dessas dez metas. Mas as levamos em consideração como ponto de partida para a condução das aulas, para o planejamento das atividades e para a avaliação dos estudantes.
De modo geral, inúmeros pesquisadores, como Quendi e Darroz (2018), têm apontado dificuldades para que essas metas sejam atingidas. Algumas dessas dificuldades decorrem tanto da formação estatística insuficiente dos futuros professores de Matemática da escola básica quanto do fato de suas lacunas de formação não serem sanadas pelas disciplinas de Estatística oferecidas nas licenciaturas. Em geral, as disciplinas têm se ocupado mais de técnicas e métodos do que de seus significados, o porquê dos métodos ou que relação guardam com a Estatística a ser ensinada na escola, para além dos cálculos. Não por acaso, tal fato acarreta que professores de Matemática, ao ensinar conceitos estatísticos, acabam por reproduzir tal visão a seus alunos dos Ensinos Fundamental e Médio. Nas palavras de Castro e Filho (2015, p. 3),
a escola precisa desenvolver atividades de busca e organização de dados para incentivar os estudantes a compreender as informações, representando-as na forma de tabelas e gráficos. Para Cazorla e Utsumi (2010, p. 15), “o tratamento de dados não se limita a apresentar somente os conceitos e procedimentos, mas implica discutir como escolher o procedimento mais adequado para analisar cada situação”. Portanto, formular um plano de investigação, concebendo questões e hipóteses; verificar como será a coleta de dados; organizar os dados coletados e representá-los na forma de tabelas e gráficos; e, por fim, interpretá-los, tirando conclusões, fazem parte das habilidades que precisam ser desenvolvidas e que requisitam não só o conhecimento matemático, mas também o raciocínio lógico, a organização, o espírito investigativo e o senso crítico.
Um pouco de Estatística
Nesta seção, iremos descrever de modo resumido os conceitos estatísticos que foram trabalhados com os alunos. Começamos com o entendimento da Estatística como ciência, como
conjunto de ferramentas para obter, resumir e extrair informações relevantes de dados; encontrar e avaliar padrões mostrados pelos mesmos; planejar levantamentos de dados ou delinear experimentos e comunicar resultados de pesquisas quantitativas. Sua importância reside no auxílio ao processo de pesquisa, que permeia todas as áreas do conhecimento que lidam com observações empíricas. Assim, podemos dizer que a Estatística é a ciência do significado e uso dos dados (Cazorla et al, 2017, p. 14).
Toda pesquisa observa um grupo de indivíduos, objetos, animais ou quaisquer elementos que possuam pelo menos uma característica comum. Na estatística, esse grupo é chamado população estatística ou população.
É feito então o estudo (coleta de dados) de certas características dos elementos dessa população; essas características são chamadas de variáveis. As variáveis podem ser: qualitativas: valores não numéricos (esporte, cor etc.) ou quantitativas: valores numéricos. As qualitativas podem ser: nominais (sem ordenação – sexo: feminino e masculino) ou ordinais (com ordenação – grupo etário: bebê, criança, adolescente, adulto e idoso). Já as quantitativas podem ser: discretas (valores inteiros, resultado de uma contagem – número de irmãos) ou contínuas (valores reais, resultado de uma medição – alturas). Precisamos prestar atenção ao fato de que muitas vezes, apesar de a resposta ser numérica, ela pode não ser quantitativa. Por exemplo, a variável idade, quando é medida em anos completos, é quantitativa (contínua); mas, se for analisada a faixa etária (0 a 5 anos, 6 a 10 anos etc.), é qualitativa (ordinal). Outro exemplo: se perguntamos o peso de lutadores de boxe, esta é uma variável quantitativa (contínua), mas se decidimos trabalhar com a categoria a que ele pertence (peso-pena, peso-leve, peso-pesado etc.), a variável será qualitativa (ordinal).
Distribuição de frequência absoluta
Para explicar a distribuição de frequência absoluta (F. A.), vamos utilizar um exemplo já retirado das pesquisas realizadas pelos alunos. Um grupo realizou a seguinte pergunta: “Quanto tempo em média você leva para terminar uma prova?”. As 25 respostas obtidas foram, em minutos: 70, 75, 60, 45, 60, 60, 60, 90, 75, 60, 90, 75, 90, 90, 90, 75, 75, 60, 45, 60, 60, 90, 70, 90, 60. Vamos então construir uma tabela de frequência com os dados coletados:
Tabela 1: Tempo médio para terminar uma prova
Tempo (minutos) |
Frequência (nº de alunos) |
45 |
2 |
60 |
9 |
70 |
2 |
75 |
5 |
90 |
7 |
Total |
25 |
Ou seja, basta listar os resultados numa tabela com duas colunas, em que na primeira dispomos em cada linha as respostas obtidas e ao lado listamos o número de vezes que cada resposta aparece.
Distribuição de frequência relativa
A frequência relativa (F. R.) é apresentada em porcentagem; para obtê-la, basta dividir cada frequência absoluta pelo valor total e escrever o valor encontrado na forma percentual. Utilizando os mesmos dados da tabela anterior, temos:
Tabela 2: Tempo médio para terminar uma prova, em porcentagem
Tempo (em minutos) |
Frequência absoluta (nº de alunos) |
Frequência relativa (em porcentagem) |
45 |
2 |
2/25=0,08 = 8% |
60 |
9 |
9/25=0,36 = 36% |
70 |
2 |
2/25=0,08 = 8% |
75 |
5 |
5/25=0,20 = 20% |
90 |
7 |
7/25=0,28 = 28% |
Total |
25 |
100% |
Distribuição de frequência para dados agrupados
Muitas vezes os dados coletados estão muito dispersos entre si. Nesses casos é aconselhável ou mais interessante fazer uma tabela de frequência para dados agrupados em intervalos (classes), a fim de não dispormos de uma tabela com diversas linhas em que a frequência é sempre igual a 1. Utilizando a notação de intervalo, a fim de um mesmo valor não pertencer a duas linhas usamos de forma convencional intervalos fechados à esquerda e abertos à direita (dependendo da situação, podemos usar a situação contrária – abertos à esquerda e fechados à direita). Sendo assim, se escrevemos [10 , 15[ ou [10 , 15) ou ainda 10 15 queremos dizer que o valor 10 pertence ao intervalo (a classe começa exatamente em 10) e o valor 15 não pertence ao intervalo (o intervalo termina no último número real antes do 15). Novamente, vamos utilizar como exemplo informações obtidas pelos alunos para exemplificar essa situação, porém já organizaremos os dados em uma tabela contendo as frequências absoluta e relativa.
Um grupo perguntou à sua turma de coleta: “Quantas canetas você possui em seu estojo?”. As 22 respostas obtidas foram: 9, 21, 20, 22, 25, 3, 6, 15, 29, 33, 10, 19, 2, 16, 14, 3, 20, 2, 4, 10, 14, 15. Agrupando as respostas em intervalos de amplitude 5 temos:
Tabela 3: Número de canetas no estojo - frequências absoluta e relativa
Número de canetas |
Frequência absoluta (nº de alunos) |
Frequência relativa (em porcentagem) |
0 5 |
5 |
5/22=0,2273 = 22,73% |
5 10 |
2 |
2/22=0,0909 = 9,09% |
10 15 |
4 |
4/22=0,1818 = 18,18% |
15 20 |
4 |
4/22=0,1818 = 18,18% |
20 25 |
4 |
4/22=0,1818 = 18,18% |
25 30 |
2 |
2/22=0,0909 = 9,09% |
30 35 |
1 |
1/22=0,0455 = 4,55% |
Total |
22 |
100% |
Metodologia
Os autores deste artigo trabalham de forma compartilhada a disciplina de Matemática para duas turmas de 3ª série do Ensino Médio. O trabalho realizado dividiu as duas turmas em grupos de três ou quatro alunos. Para cada grupo, foi selecionada uma turma do mesmo turno em que estudam na escola, de modo que todas as turmas desse turno fossem utilizadas apenas uma vez, desde o 6º ano do Ensino Fundamental até a 3ª série do Ensino Médio. A proposta era que cada grupo confeccionasse um questionário com quatro perguntas e aplicasse na turma previamente escolhida para eles. As perguntas teriam que admitir respostas curtas; duas perguntas deveriam admitir respostas (variáveis) qualitativas e as outras duas respostas, quantitativas. Além disso, as duas respostas quantitativas precisavam ser uma discreta e uma contínua.
Após a aplicação do questionário, os grupos foram instruídos a organizar as informações construindo tabelas de frequência absoluta e relativa das informações coletadas, bem como um gráfico para cada tipo de variável (um gráfico de uma das variáveis quantitativas e um gráfico de uma das variáveis qualitativas). Foi solicitado que os grupos conversassem previamente entre si para que diversificassem as perguntas, porém obtivemos muitas perguntas similares ou mesmo iguais em grupos distintos.
Após as construções dos gráficos e tabelas, os alunos deveriam ainda escrever alguma conclusão ou informação relevante que pudesse ser observada nos gráficos ou tabelas.
Dificuldades encontradas para a execução do trabalho
As principais dificuldades encontradas pelos alunos serão relatadas a seguir. Dentre elas, podemos citar a escolha das variáveis dentro das regras estabelecidas. Já prevendo essas e outras dificuldades, as instruções do trabalho indicavam a necessidade de mostrar as perguntas previamente escolhidas para os professores antes da aplicação efetiva do questionário.
Por exemplo, um aluno de um grupo escolheu fazer a seguinte pergunta: “Quanto você calça?”, classificando-a como variável quantitativa contínua, alegando que o tamanho do pé é um valor contínuo. Então conversamos que, apesar de o tamanho do pé ser de fato contínuo, o número dos sapatos é fornecido em valores discretos (35, 40, 43...).
Outra dificuldade encontrada foi a necessidade que os alunos tinham em resumir previamente as respostas coletadas. Um grupo resolveu perguntar: “Quantos livros em média você lê por ano?”, classificando-a como variável quantitativa discreta. Porém elaborou o questionário fornecendo faixas de resposta para marcação:
( ) 0 – 5 ( ) 5 – 10 ( ) 10 – 15 ( ) 15 – 20 ( ) mais de 20
Foi explicado então que, quando apresentamos faixas de resposta para uma variável quantitativa, muitas vezes estamos analisando na verdade um aspecto qualitativo. Nesse caso poderíamos reescrever a pergunta como: “Como você classifica sua frequência de leitura por ano?”, fornecendo como opção de resposta estas alternativas:
( ) baixa ( ) média ( ) alta ( ) elevada ( ) muito elevada
Como vários grupos apresentaram dúvidas similares a essa, todos os grupos foram então orientados a colher as respostas quantitativas sempre de forma aberta, ou seja, não colocar opções para as respostas quantitativas. Então, com os questionários respondidos em mãos, foram analisar e avaliar a necessidade ou não de agrupar os dados, para construir a tabela de frequência solicitada em valores absolutos ou em dados agrupados.
Outro relato apresentado pelos alunos foi a dificuldade que as pessoas têm de responder um questionário simples. Um grupo apresentou a pergunta a seguir, exatamente assim:
“Qual seu gênero musical favorito? (escolha apenas um)”
( ) MPB ( ) Rock ( ) Pop ( ) Hip Hop ( ) Funk ( ) Outro: ______
Dentre os 27 alunos que responderam, vários marcaram duas opções, mesmo o questionário pedindo apenas um gênero, ou então marcaram uma das opções oferecidas, porém também responderam outro gênero no campo “outro”. E aí conversamos com os alunos sobre o quanto as pesquisas podem ser “manipuladas” pelo seu autor; uma vez que a resposta não foi feita dentro do padrão solicitado, não sabemos como o autor gerenciou esse tipo de resposta: se descartou toda a resposta ou escolheu apenas uma das opções fornecidas.
Perguntas elaboradas pelos alunos
Abaixo vamos discriminar algumas das principais perguntas realizadas, separadas pelas quatro classificações das variáveis. Apesar de o trabalho em si não exigir a necessidade de que as variáveis qualitativas fossem uma ordinal e uma nominal, alguns grupos assim o fizeram. As perguntas estão transcritas exatamente como os alunos as elaboraram.
- Perguntas cujas respostas são variáveis qualitativas ordinais:
“Como você qualifica o transporte púbico?”; “Em que mês você nasceu?”.
- Perguntas cujas respostas são variáveis qualitativas nominais:
“Qual esporte costuma praticar?”; “Qual matéria escolar vocês acham mais difícil?”; “Qual país você tem vontade de conhecer?”; “Você é de humanas, exatas ou biológicas?”; “Qual a cor do seu cabelo?”, “Qual graduação você deseja cursar? (caso esteja em dúvida, escreva em dúvida. Caso não pretenda cursar nenhuma, escreva nenhuma)”; “Qual o seu gênero musical favorito? (escolha apenas um)”.
- Perguntas cujas respostas são variáveis quantitativas discretas:
“Quantas refeições você faz por dia?”; “De quantos grupos do WhatsApp você participa?”; “Quantos livros você leu este ano? (Caso não tenha lido nenhum, escreva 0)”.
- Perguntas cujas respostas são variáveis quantitativas contínuas:
“Saindo às 12h da escola, a que horas você chega em casa?”; “Quantas horas de sono você aproximadamente tem por dia?”; “Qual a sua altura?”; “Quanto tempo você costuma demorar para fazer a prova de Geografia da escola? (Considere o total como 1h30)”.
Principais erros encontrados e considerações feitas
Agora vamos citar alguns dos erros e principais problemas encontrados.
Na pergunta “Quantas refeições você faz por dia?”, as respostas obtidas foram: 6, 4, 2, 5, 5, 3, 5, 5, 4, 5, 5, 5, 4, 4, 3. E a tabela apresentada pelo grupo foi:
Tabela 4: Quantidade de refeições diárias (construção errada)
Pessoas |
F. A. |
F. R. |
1 |
1 |
5,26% |
1 |
6 |
31,58% |
2 |
3 |
15,79% |
4 |
4 |
21,05% |
7 |
5 |
26,31% |
Total |
19 |
100% |
Notamos que os alunos do grupo não entenderam perfeitamente o conceito de variável e como construir uma tabela de frequência. Como a pergunta era sobre o número de refeições, na primeira coluna onde estavam os dados/informações coletadas é que deveriam aparecer os números de refeições realizadas (2, 3, 4, 5, 6), enquanto o número de pessoas que respondeu cada valor correspondente à frequência daquela quantidade de refeições deveria estar na segunda coluna. Um ponto de destaque da tabela é o fato de uma pessoa ter respondido que faz apenas uma refeição por dia. Isso traz o questionamento se, quando fazemos uma pesquisa, aquela resposta destoante representa alguém que não entendeu a pergunta; alguém que aplicou uma definição diferente para refeição, pois a noite só faz lanches; alguém que realmente só faz uma refeição por dia por sua situação financeira ou alguma dieta pessoal. Quando solicitamos que os alunos fizessem comentários sobre as tabelas, era para que atentassem a fatos como esse, para os quais, quando temos os questionários respondidos em mãos, não prestamos atenção, mas com a tabela pronta percebemos esses tipos de respostas. Nesse caso, foi apenas um erro de transcrição, como pode ser visto nas respostas listadas acima: na verdade, um aluno afirmou que fazia duas refeições por dia, e não uma refeição.
Outro grupo apresentou uma tabela relativa à quantidade de aparelhos de telefonia fixa ou de celular em sua residência.
Tabela 5: Número de telefones fixos ou celulares por residência
Números de celulares ou telefones fixos |
F. A. |
F. R. |
1 |
1 |
3,33% |
2 |
3 |
10% |
3 |
4 |
13,33% |
4 |
12 |
40% |
5 |
2 |
6,67% |
6 |
5 |
16,66% |
7 |
2 |
6,67% |
8 |
1 |
3,33% |
Total |
30 |
100% |
Sobre a tabela construída, os alunos escreveram a seguinte análise: “podemos perceber que pouco menos da metade da turma possui 12 aparelhos fixos ou celulares em suas residências”. Como esse grupo não entregou os questionários respondidos, não foi possível listar as respostas obtidas. Partindo unicamente da tabela construída, consideramos que esse comentário demonstra que os alunos não apreenderam o conceito de frequência absoluta, já que a informação “12” se refere a uma quantidade de pessoas – e não de aparelhos de telefonia.
Outro exemplo: na pergunta “De quantos grupos de WhatsApp você participa?”, as respostas coletadas foram: 11, 8, 20, 32, não sei, 2, 25, 10, 62, 4, 38, 60, 3, 51, 40, 6, 10, 20, 10, 0, 7, 25, 10, 9, 10. E os alunos apresentaram a tabela a seguir:
Tabela 6: Número de grupos de WhatsApp por pessoa - Dados isolados
Grupos do WhatsApp |
F. A. |
F. R. |
0 |
1 |
4% |
2 |
1 |
4% |
3 |
1 |
4% |
4 |
1 |
4% |
6 |
1 |
4% |
7 |
1 |
4% |
8 |
1 |
4% |
9 |
1 |
4% |
10 |
5 |
20% |
11 |
1 |
4% |
20 |
2 |
8% |
25 |
2 |
8% |
32 |
1 |
4% |
38 |
1 |
4% |
40 |
1 |
4% |
51 |
1 |
4% |
60 |
1 |
4% |
62 |
1 |
4% |
Não sabe |
1 |
4% |
Total |
25 |
100% |
Como essa pergunta estava dentro da exigência de que uma das perguntas admitisse resposta quantitativa, não caberia a resposta “não sei”. Os alunos precisavam ter colocado: “caso não saiba, responda zero”, ou “caso não saiba, estime um valor”. Recaímos no problema do cuidado na confecção do instrumento de coleta para não obter respostas fora do padrão necessário. No caso de um trabalho mais técnico, é possível usar questionários online que limitam ou restringem respostas nominais em campos que precisam ser numéricos ou vice-versa. Outro problema apresentado foi o fato de não ter usado uma tabela para dados agrupados. Como praticamente todas as respostas tiveram frequência igual a 1, se tivessem usado classes de frequência os resultados ficariam menos dispersos. Descartando a pessoa que respondeu “não sei”, teríamos:
Tabela 7: Número de grupos de WhatsApp por pessoa - Dados agrupados
Grupos do WhatsApp |
F. A. |
F. R. |
0 10 |
8 |
33,33% |
10 20 |
6 |
25% |
20 30 |
4 |
16,67% |
30 40 |
2 |
8,33% |
40 50 |
1 |
4,17% |
50 60 |
1 |
4,17% |
60 70 |
2 |
8,33% |
Total |
24 |
100% |
Ressaltamos que a tabela apresentada pelos alunos não está errada, mas muitas vezes uma tabela ou um gráfico com quantidade elevada de informações atrapalha ou mesmo dificulta a apreensão clara e rápida das informações por parte do leitor.
Outro grupo fez a seguinte pergunta: “Quantos primos de 1º grau você possui?”. As respostas coletadas foram 16, 8, 7, 1, 15, 10, 16, 2, 8, 9, 4, 14, 10, 12, não sei, 15, não sei, 12, 15, 5, 5, 6, 10, 1, 3 e 5. Os alunos desse grupo apresentaram sua tabela.
Tabela 8: Número de primos de 1º grau
Primos de primeiro grau |
F. A. |
F. R. |
0 à 5 |
7 |
28% |
5 à 10 |
8 |
32% |
10 à 16 |
8 |
32% |
Não sabem |
2 |
8% |
Total |
25 |
100% |
Vários erros foram encontrados nesta tabela. Assim como foi citado no exemplo anterior, eles deveriam ter descartado as respostas “não sei”, por se tratar de uma pergunta cuja resposta deveria ser quantitativa e ter usado somente 24 informações. Outro ponto de destaque é que na verdade foram coletadas 26 respostas e eles usaram apenas 25, provavelmente para facilitar o cálculo da frequência relativa. Por fim, as classes utilizadas estão erradas, já que as classes têm que ter o mesmo tamanho. Então, como não há resposta 0, as classes poderiam ser [1, 7[, [7, 13[ e [13, 19[ ou então ]0, 6], ]6, 12] e ]12, 18], ou ainda ter colocado quatro classes: ]0, 4], ]4, 8], ]8, 12] e ]12, 16], que contemplam as quantidades de 1 a 16, que foram as respostas encontradas.
Além dos erros e problemas encontrados na construção das tabelas, o uso dos gráficos apropriados foi também um ponto de muitos erros cometidos. A maioria usou sem critério gráficos de pizza, simplesmente clicando na opção “fazer gráfico de pizza” com o programa que estavam utilizando.
O gráfico de pizza não é usado para variáveis quantitativas, assim como para classes de dados. Tal situação possibilitou ressaltar com os alunos um dos papéis da tecnologia: o software utilizado fará aquilo que lhe for pedido, mesmo nos casos em que a ação solicitada não faça nenhum sentido. Cabe ao usuário do programa ter o discernimento sobre fazer ou não sentido aquilo que se está pedindo que o programa faça.
Apresentamos a seguir algumas imagens, digitalizadas dos próprios trabalhos dos alunos, para exemplificar o uso incorreto do gráfico de pizza.
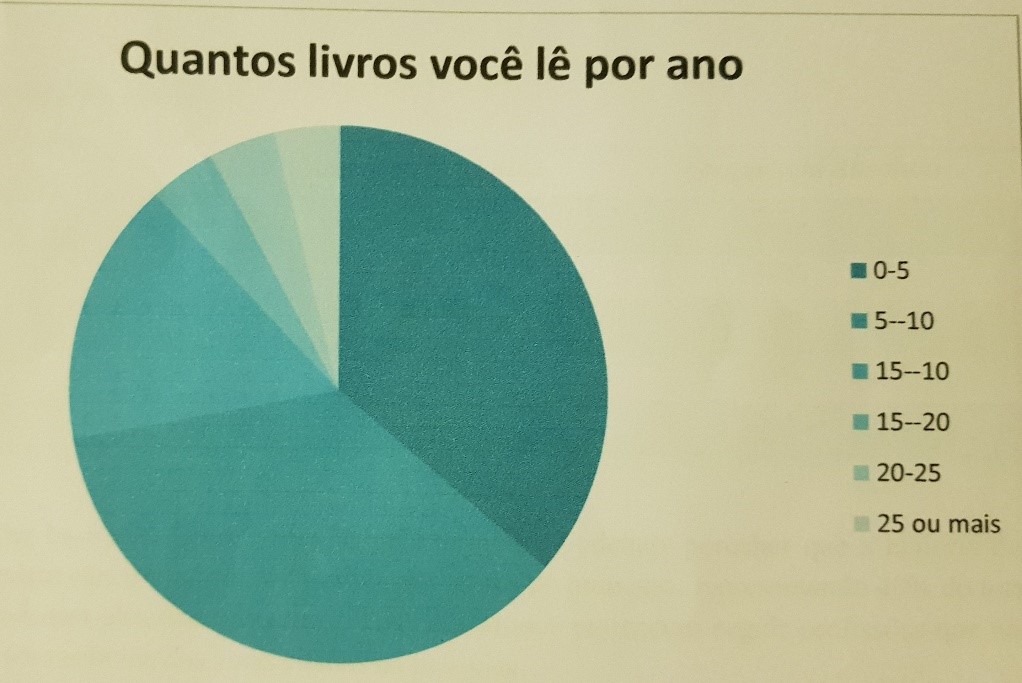
Figura 1: Gráfico "Número de livros lidos por ano" – Construção errada
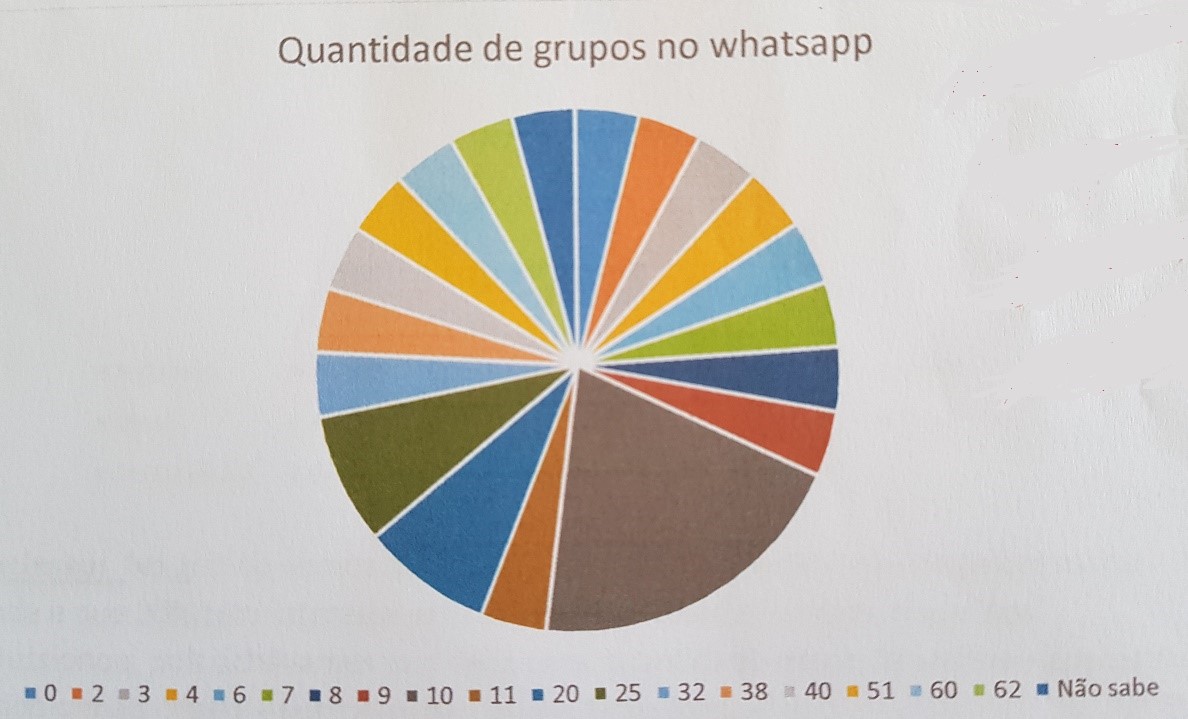
Figura 2: Gráfico "Número de grupos de WhatsApp por pessoa" – Construção errada
Aqui vemos o uso de um gráfico não apropriado para a variável em questão, que é quantitativa. Segundo Serrano, Silva e Velasque (2010, p. 7),
Na hora de escolher um gráfico é fundamental saber se é apropriado para o tipo de variável. Um gráfico de pizza só é apropriado para representar variáveis qualitativas nominais (com poucos atributos), mas o gráfico de barras pode representar bem tanto as variáveis qualitativas nominais quanto as ordinais. Na representação de uma variável quantitativa contínua, o histograma ou boxplot são os mais apropriados.
Esse gráfico ainda sofre de um excesso de “fatias”, o que o faz perder uma das coisas que um gráfico possui de importante: apresentar as informações de modo rápido. De acordo com Campos e Coutinho (2019, p. 13), “uma das finalidades da representação gráfica é proporcionar uma interpretação ágil e fácil do comportamento global da variável”; os dois gráficos anteriores não apresentam aspecto visual agradável ou de interpretação rápida. Na Figura 1, por exemplo, a escala de cores utilizada não foi feliz; na Figura 2, o excesso de classes torna o gráfico de visualização confusa e desagradável.
Outro ponto de destaque é o fato de também não usarmos gráfico de pizza para variáveis qualitativas ordinais, pois, como o próprio nome diz, a variável necessita uma ordenação que o gráfico de pizza não permite; o gráfico da Figura 4 ressalta essa informação; o gráfico de pizza não apresenta ordenação: todas as faixas estão dispostas de forma semelhante, o que varia é o tamanho da região, de acordo com a porcentagem (ou frequência) que aquela resposta representa do total.
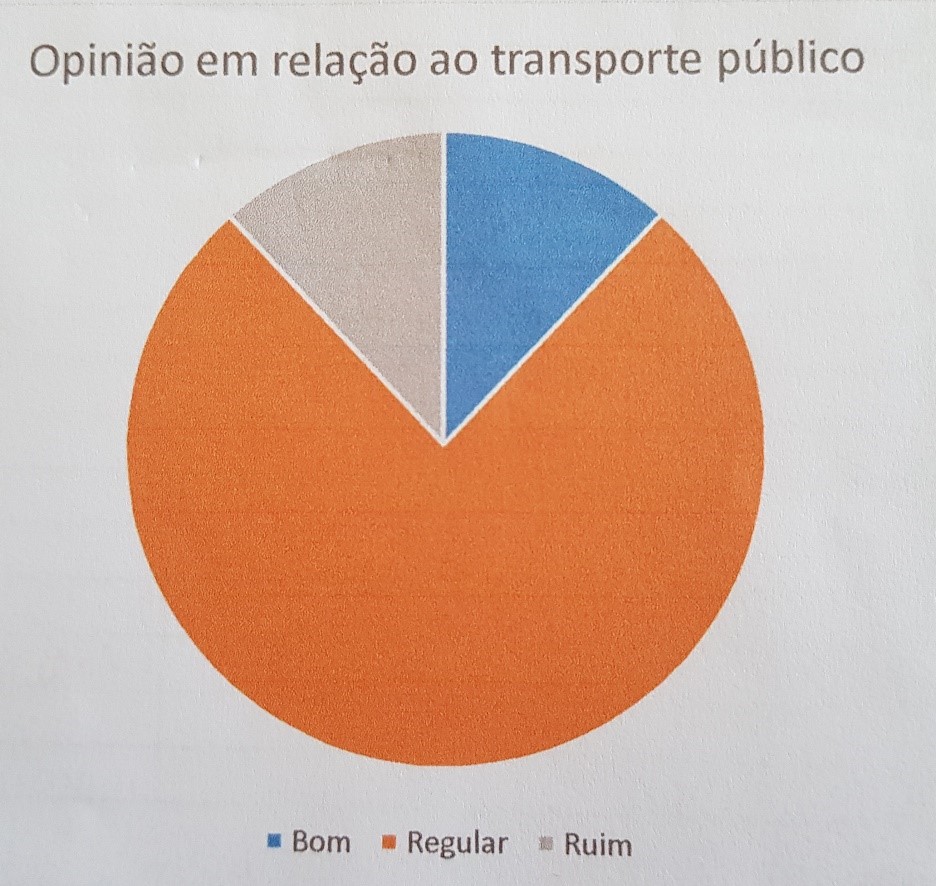
Figura 3: Gráfico "Opinião pessoal sobre o transporte público”
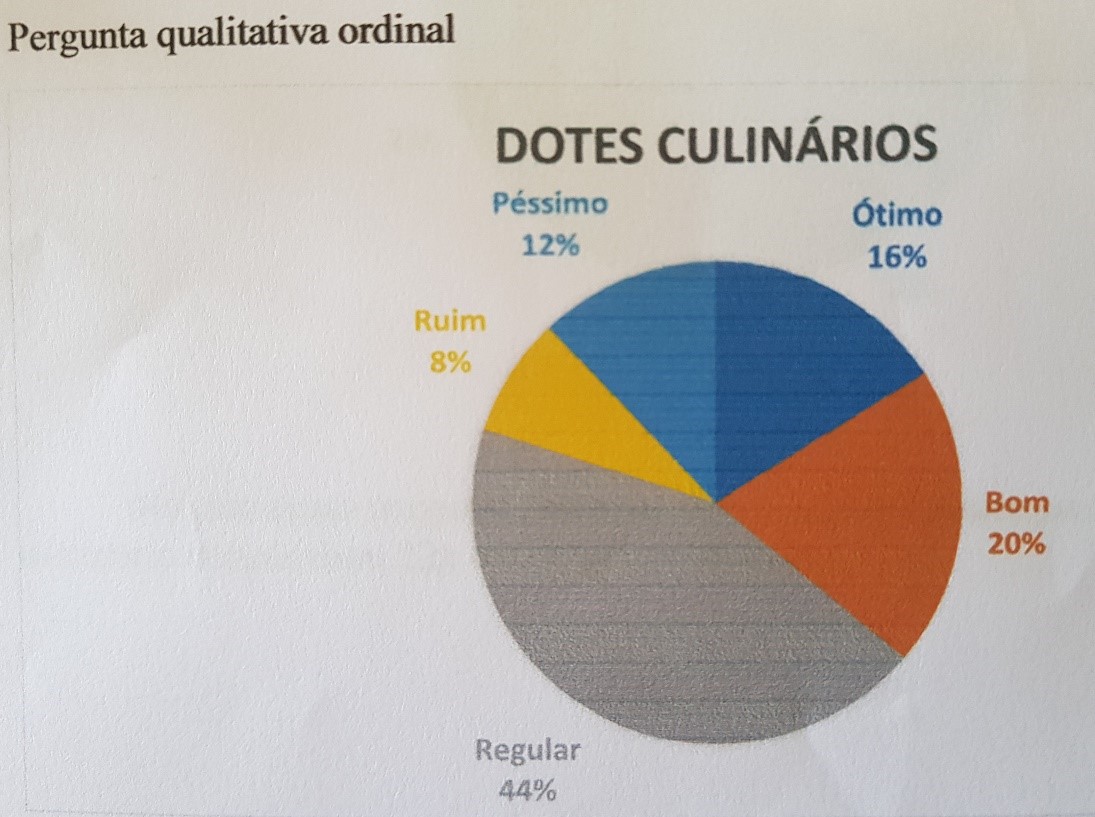
Figura 4: Gráfico "Qualificação pessoal sobre seus dotes culinários"
Os gráficos de barras também apresentaram problemas. O gráfico da Figura 5 não está errado, porém o programa utilizado acrescenta uma barra total, que, segundo os alunos, não é possível remover. Porém o leitor pouco atento ou pouco orientado estatisticamente pode acreditar que existe uma classe que apresentou aquela resposta, ou seja, que aquela barra representa um grupo – e não que representa o total. Com isso, destacamos as pesquisas das mídias em que sempre os gráficos e tabelas aparecem de forma muito rápida e superficial, não permitindo que nos atentemos a esses detalhes. Uma conclusão similar foi destacada por Castro e Filho, que fizeram um trabalho estatístico com o uso de suporte computacional e afirmam que
a pesquisa de Mendonça e Lopes (2011) prevê a utilização da tecnologia por meio do software Excel, entretanto, ela foi usada apenas para a construção de tabelas e gráficos, após a coleta de dados. Castro (2012) explica que esse tipo de programa não permite a reflexão sobre a construção, pois gera os gráficos automaticamente (2015, p. 7).
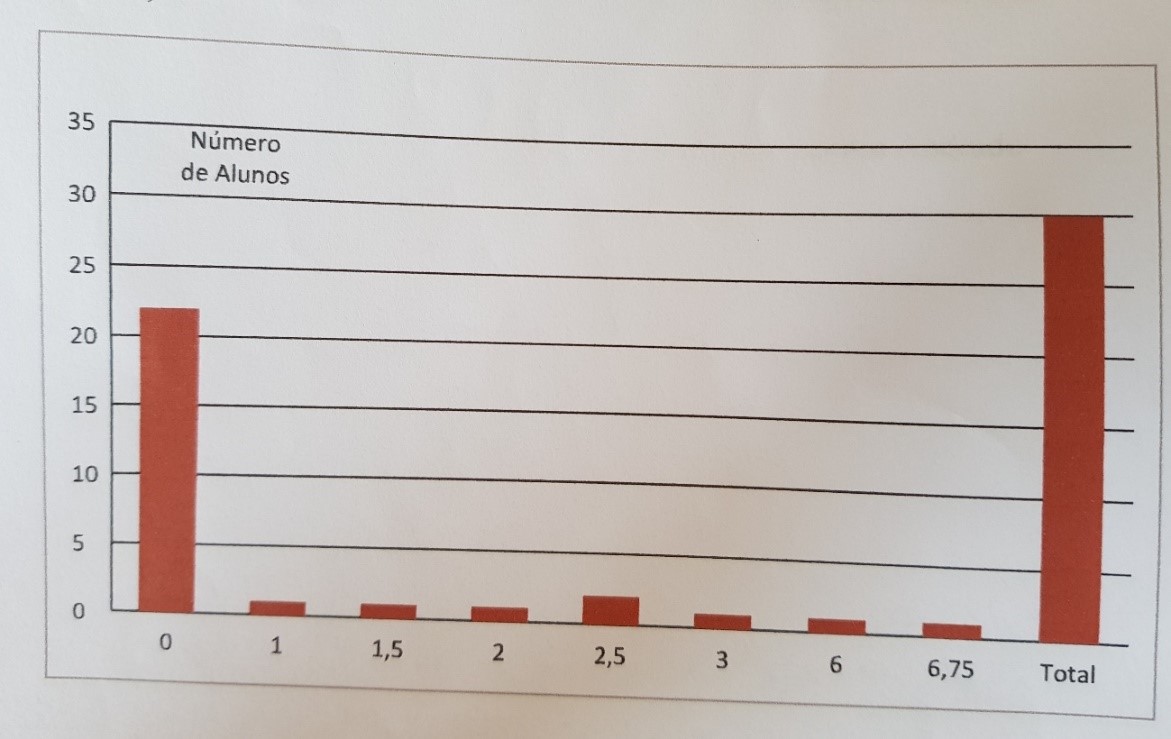
Figura 5: Gráfico "Maior grau de miopia por pessoa"
Por fim vemos um grupo de alunos que fez uma representação gráfica de intervalos com barras isoladas e fez questão de escrever os intervalos, em que a primeira barra azul se encerra em 3h59min e a barra seguinte começa em 4h, porém com um “buraco” entre as barras, mostrando completo desconhecimento da definição de reta numérica e intervalos reais, conteúdo aprendido na 1ª série do Ensino Médio.
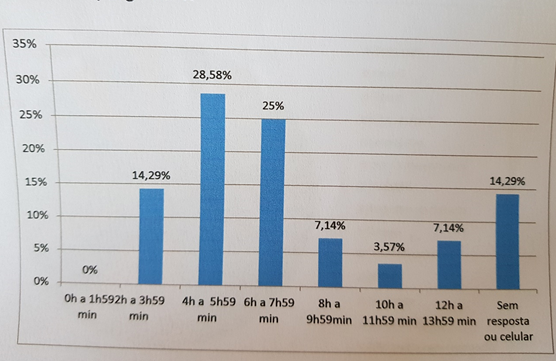
Figura 6: Gráfico de tempo médio que fica no celular por dia
Outro erro que se mostrou presente nos gráficos de barra de um grupo que os fez à mão livre remete a lacunas de conceitos matemáticos: escala. O grupo fez a pergunta “Qual a cor dos seus olhos?”, com as opções de resposta azul, castanho claro, castanho escuro, preto e verde. As respostas obtidas foram: castanho claro, castanho escuro, castanho escuro, castanho claro, castanho escuro, verde, castanho claro, castanho escuro, castanho escuro, castanho claro, castanho escuro, castanho escuro, castanho escuro, preto, castanho escuro, castanho escuro, castanho escuro, preto, castanho escuro, castanho claro, castanho escuro, preto, castanho claro, preto, castanho claro e castanho escuro. O gráfico apresentado pelo grupo foi o seguinte:
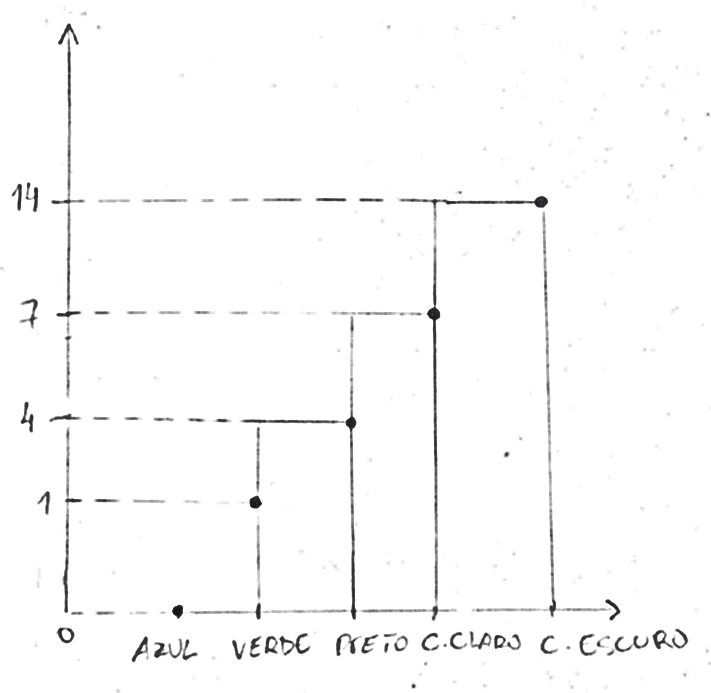
Figura 7: Gráfico "Qual é a cor dos seus olhos?"
Podemos perceber no gráfico que os alunos incluíram a resposta azul apenas pelo fato de ela ser uma das opções de resposta no questionário, mesmo que tal resposta não tendo sido mencionada por qualquer um dos entrevistados. Além disso, os números aparecem no eixo vertical de modo desproporcional aos seus valores. Esse erro foi encontrado nos demais gráficos de barra desse grupo e em vários grupos que construíram os gráficos de barra à mão livre. Tal fato levanta o questionamento se os grupos que construíram os gráficos de barra diretamente em aplicativos ou softwares não teriam também errado caso os tivessem feito à mão livre.
Destaques interessantes
Para a pergunta “Quanto tempo você costuma demorar para fazer a prova de Geografia da escola? (Considere o total como 1h30min)”, as respostas foram (já convertidas para minutos): 90, 90, 60, 60, 60, 45, 75, 68, 50, 80, 40, 80, 40, 60, 40, 90, 70, 70, 60, 70, 50, 60, 90, 60, 45, 80, 45. Alguns problemas encontrados foram: houve alunos que escreveram como resposta, por exemplo, “entre 1h e 1h30min”, sem especificar o tempo. O grupo então considerou a resposta como 75 minutos. A aluna do grupo que estava encarregada dessa distribuição sentiu dificuldade em compor as classes. Especificamente em colocar os intervalos em apenas três classes [30 , 60), [60 , 90) e [90 , 120) ela não viu coerência, já que o valor máximo era 90 e a última classe abrangia somente o número 90 como possível. Além disso, ela achou que três classes era pouco e então, após conversarmos, chegamos juntos às classes apresentadas na próxima tabela. Foi bem interessante a aluna perguntar se a classe podia ser disposta num intervalo aberto à direita e fechado à esquerda. Reforçamos que a convenção faz o contrário, mas que nesse caso, como ninguém respondeu 30 minutos e como 90 foi uma resposta muito usada, a tabela na configuração abaixo se torna muito mais interessante.
Tabela 9: Tempo médio para realizar a prova de Geografia
Tempo (em min) |
F |
Fr |
] 30 45 ] |
6 |
22,22% |
] 45 60 ] |
9 |
33,33% |
] 60 75 ] |
5 |
18,52% |
] 75 90 ] |
7 |
25,93% |
Total |
27 |
100% |
Outro destaque foi o comentário dos alunos sobre acharem muito mais interessante ter feito os gráficos e tabelas a partir de dados coletados por eles do que fazer análises de informações sem sentido, inventadas e dispostas em tabelas prontas ou no livro. Consideramos esse um retorno muito positivo do trabalho e que reforçou as conclusões de diversos pesquisadores já mencionados neste artigo. Além disso, como os alunos tinham a liberdade de escolher as perguntas que seriam utilizadas, encontramos algumas bastante interessantes e curiosas, que dificilmente encontraríamos em qualquer material de estatística para ilustrar gráficos e distribuição de frequência.
Considerações finais
Com este trabalho verificamos que os alunos chegam à 3ª série do Ensino Médio, ou seja, ao final da Educação Básica, com uma defasagem muito grande de conceitos estatísticos prévios, dificuldade na leitura e interpretação dos dados. Muitos deles chegam à última série da Educação Básica sem sequer ter estudado qualquer conceito simples de estatística, daí as falhas citadas no decorrer deste trabalho. Também observamos a falta de conhecimento prévio do uso apropriado de cada tipo de gráfico que conhecem. A maioria apenas selecionou os dados e clicou na ferramenta do programa utilizado, Excel ou similares, e escolheu a opção “Fazer gráfico de pizza” ou “Fazer gráfico de barras” sem sequer avaliar se aquele modelo cabia para aquela situação. Como a mídia apresenta sistematicamente gráficos de barras e pizzas e esses modelos estão tão facilmente oferecidos nos programas básicos, eles aplicaram o recurso de forma espontânea.
Outra etapa em que os alunos também apresentaram muitas dificuldades foi na construção das tabelas, da organização efetiva dos dados: tendo as respostas do questionário em mãos, como fazer a mudança de registro dos dados em papel para a construção do “banco de dados” e então para as tabelas de frequência e os gráficos.
Por outro lado, os alunos se mostraram bastante interessados e empolgados na execução do trabalho; a maioria se mostrou empenhada no cumprimento das tarefas solicitadas e preocupada na elaboração das perguntas e na aplicação do questionário. Era necessário entregar todos os questionários aplicados, e dos 19 grupos apenas um não cumpriu essa etapa do trabalho. Após essa atividade, pudemos observar que os alunos apresentaram mais facilidade na construção de tabelas de frequência absoluta ou relativa para dados agrupados ou isolados. Esse fato esteve relacionado principalmente ao fato de eles terem praticado e executado manualmente todo o processo de coleta, organização e tabulação dos dados.
Outro ponto positivo foi ver a criatividade na elaboração das perguntas: como citamos, o estudo de gráficos e tabelas foi feito com base em perguntas não usuais, mas completamente dentro do cotidiano dos alunos. Estamos acostumados com as listas de dados padrão – peso, altura, cor dos olhos e notas – e neste trabalho os alunos puderam tabular o “Vingador preferido”, número de grupos de WhatsApp, horas de sono, cor de cabelo...
Mais um retorno positivo foi que a questão de prova que abordava a construção de uma tabela de frequências absolutas e relativas dada uma lista prévia de dados foi bem aproveitada pela grande maioria dos alunos.
Por fim, pudemos perceber que o aprendizado dos conceitos estatísticos foi mais produtivo com a pesquisa concreta e a execução prática por parte dos alunos, e que esse modelo de trabalho, ensino e avaliação poderia ser estendido para os demais conceitos estatísticos, como trabalhar com as medidas estatísticas de resumo e variabilidade, além de maior aprofundamento nos modelos de gráficos.
Referências
BRASIL. MEC. SECRETARIA DE EDUCAÇÃO BÁSICA. Parâmetros Curriculares Nacionais do Ensino Médio. Brasília: MEC/SEB, 2006.
______. PCN + Ensino Médio: Orientações educacionais complementares aos Parâmetros Curriculares Nacionais. Brasília: MEC/SEB, 2006.
______. MEC. SECRETARIA DE EDUCAÇÃO FUNDAMENTAL. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1998.
CAMPOS, C.; COUTINHO, C. O letramento estatístico e a modelagem matemática no ensino de gráficos. Caminhos da Educação Matemática em Revista [Online], v. 9, nº 2, 2019.
______; WODEWOTZKI, M. L.; JACOBINI, O. Educação Estatística: teoria e prática em ambientes de modelagem matemática. Belo Horizonte: Autêntica, 2011. (Coleção Tendências em Educação Matemática).
CASTRO, J.; FILHO, J. Desenvolvimento do pensamento estatístico com suporte computacional. Educ. Matem. Pesq., São Paulo, v. 17, nº 5, p. 870-896, 2015.
CAZORLA, I.; MAGINA, S.; GITIRANA, V.; GUIMARÃES, G. Estatística para os anos iniciais do Ensino Fundamental. São Paulo: SBEM, 2017.
GAL, I.; GARFIELD, J. Teaching and assessing statistical reasoning. In: DEVELOPING MATHEMATICAL REASONING IN GRADES K-12. National Council of Teachers of Mathematics. Reston: Ed. L. Staff, 1999. p. 207-219.
LOPES, C. E. Os desafios para a Educação Estatística no currículo de Matemática. In: LOPES, C. E.; COUTINHO, C. de Q. e S.; ALMOULOUD, S. A. (Orgs.). Estudos e reflexões em Educação Estatística. Campinas: Mercado de Letras, 2010.
QUENDI, R. P.; DARROZ, L. M. Conceitos básicos de Estatística: as lacunas conceituais de acadêmicos ingressantes no curso superior. Thema, v. 15, nº 4, 2018.
SERRANO, T.; SILVA, A.; VELASQUE, L. Ensino de Estatística para os anos iniciais e finais da educação básica utilizando metodologia ativa e o programa computacional R. GAE: Grupo de Apoio Estatístico - UNIRIO. X ENEM, 2010. Anais...
Publicado em 16 de março de 2021
Como citar este artigo (ABNT)
SANTOS, Geisa Abreu Lira Corrêa dos; ALVES, Renato de Carvalho. Um relato/estudo sobre o uso de atividades investigativas para o ensino de estatística na educação básica. Revista Educação Pública, v. 21, nº 9, 16 de março de 2021. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/21/9/um-relatoestudo-sobre-o-uso-de-atividades-investigativas-para-o-ensino-de-estatistica-na-educacao-basica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

