O uso de metodologias ativas no ensino das funções trigonométricas: uma adequação para o novo Ensino Médio
Juliana Abrantes Tavares
Licenciada em Matemática, mestranda do Profmat/UnB
Leonardo Henrique Santos Simões
Licenciado em Matemática, mestrando do Profmat/UnB
Wescley Well Vicente Bezerra
Doutor em Educação, professor da UnB e do Profmat/UnB
Tatiane da Silva Evangelista
Doutora em Matemática, professora da UnB e do Profmat/UnB
A Trigonometria é uma vertente da Matemática que surgiu da necessidade de se calcular grandes distâncias, inviáveis de serem medidas fisicamente. A palavra trigonometria, do grego trigonon (triângulo) e metron (medida) remete ao estudo dos ângulos e lados dos triângulos, figuras básicas em qualquer estudo de Geometria (Iezzi et al., 2016, p. 214). A partir das proporções formadas com os lados dos triângulos foi possível determinar as grandes distâncias e solucionar diversos problemas posteriores. Os estudos dessas relações entre os lados e ângulos do triângulo desenvolveram-se ao longo do tempo, resultando em uma generalização que hoje conhecemos como círculo trigonométrico. Este, por sua vez, deu origem às funções trigonométricas ou periódicas, funções presentes em vários campos da Ciência, inclusive na Física aplicada nos movimentos ondulatórios.
Na Educação, a Trigonometria compõe o currículo escolar em âmbito nacional, iniciando-se no 9º ano do Ensino Fundamental, com as razões trigonométricas do triângulo retângulo (Distrito Federal, 2018, p. 97), estendendo-se ao Ensino Médio, etapa na qual são inseridos o estudo do círculo trigonométrico, identidades trigonométricas e as funções periódicas (Distrito Federal, 2018, p. 46). Nesse momento, começam a surgir obstáculos na aprendizagem do referido conteúdo, seja pela dificuldade de abstração, de visualização ou de conexão entre a Álgebra e a Geometria. Em parte, o fato se dá pela falta de uma metodologia adequada de ensino por parte dos docentes ou, ainda, por uma junção do fator anterior somado às dificuldades já existentes no aprendizado da Matemática.
Tratando-se da Matemática como um todo, a necessidade de revisar as práticas pedagógicas é uma necessidade constante diante dos cenários desafiadores vivenciados em sala de aula. É preciso buscar novas metodologias para a mediação dos conteúdos, assim como formas de instigar o interesse e a participação efetiva dos estudantes envolvidos no processo. Sopelsa, Gazzóla e Detoni (2014, p. 6) destacam a importância em rever a articulação entre a teoria e a prática no ensino da Matemática, bem como de reconhecer as demandas do Ensino Básico para construir cenários pedagógicos favoráveis ao aprendizado do referido componente curricular.
A discussão sobre a revisão das práticas pedagógicas acaba ampliando-se aos demais componentes curriculares da Educação Básica, uma vez que o Ensino Médio passará por alterações em sua estrutura com a chegada do Novo Ensino Médio (NEM). Por meio da Lei nº 13.415/17, o NEM será implementado gradativamente a partir de 2022 e suas principais mudanças se relacionam ao formato de mediação do conhecimento, deixando de ser meramente conteudista para ser um conhecimento aplicado à realidade dos alunos, voltado às relações cotidianas.
Diante do exposto, visando sanar as dificuldades já existentes no ensino da Matemática e associando esse aprendizado à necessidade de adequar as práticas pedagógicas para o NEM, convém implementar metodologias ativas de ensino, que consistem em deslocar a perspectiva do docente para o estudante (Baldez et al., 2017, p. 270). As metodologias ativas viabilizam a autonomia e o protagonismo dos estudantes, estimulando a autoaprendizagem e a curiosidade do estudante à pesquisa, à reflexão e à análise de possíveis situações para tomadas de decisão, sendo o professor apenas um facilitador desse processo (Berbel, 2011, p. 29).
Nesse sentido, o presente estudo teve como objetivo investigar e aplicar tais metodologias a um caso, em específico, de ensino das funções trigonométricas.
A Base Nacional Comum Curricular
A Lei de Diretrizes e Bases da Educação Brasileira (LDB, nº 9.394/96) prevê, em seu Art. 26, a criação de uma base nacional comum para os currículos do Ensino Básico. Esses currículos sofreram modificações ao longo do tempo e a mais recente foi instituída pela Lei nº 13.415/17, cujo produto é a Base Nacional Comum Curricular (BNCC). A BNCC é um documento que normatiza as referências curriculares, as propostas pedagógicas e as aprendizagens essenciais para a Educação Básica, em âmbito nacional, estabelecendo competências gerais e específicas, assim como os objetivos de aprendizagem e as habilidades mínimas a serem desenvolvidas e asseguradas aos estudantes.
Para a etapa do Ensino Médio, o referido documento determina que deve ser garantido aos estudantes o protagonismo em seus próprios processos de escolarização, formando sujeitos críticos, criativos, autônomos e responsáveis. Para cumprir essa determinação, o currículo do Ensino Médio passa a ser organizado em duas vertentes: a formação geral básica e os itinerários formativos. A formação geral básica é a parte responsável pelo detalhamento referente às aprendizagens essenciais e obrigatórias do currículo, divididas em quatro áreas: Linguagens e suas Tecnologias, Matemática e suas Tecnologias, Ciências da Natureza e suas Tecnologias e Ciências Humanas e Sociais Aplicadas. Já os itinerários formativos compõem a parte flexível do currículo e são norteados por quatro eixos estruturantes, a saber, a investigação científica, os processos criativos, a mediação e a intervenção sociocultural e o empreendedorismo. A princípio, as diretrizes contidas na BNCC passam a valer para o Ensino Médio a partir de 2022, obrigatoriamente, em todas as escolas do país.
No que se refere à área da Matemática e suas Tecnologias, são cinco as competências específicas, sendo a terceira delas a competência descrita a seguir:
Utilizar estratégias, conceitos, definições e procedimentos matemáticos para interpretar, construir modelos e resolver problemas em diversos contextos, analisando a plausibilidade dos resultados e a adequação das soluções propostas, de modo a construir argumentação consistente (Brasil, 2018, p. 531).
Tal competência é subdividida em dezesseis habilidades específicas, dentre as quais uma delas diz respeito ao ensino das funções trigonométricas:
(EM13MAT306) Resolver e elaborar problemas em contextos que envolvem fenômenos periódicos reais (ondas sonoras, fases da lua, movimentos cíclicos, entre outros) e comparar suas representações com as funções seno e cosseno, no plano cartesiano, com ou sem apoio de aplicativos de álgebra e geometria (Brasil, 2018, p. 536).
É necessário, portanto, reavaliar as estratégias de ensino para que as competências e as habilidades estabelecidas pela BNCC sejam garantidas aos estudantes na forma como o documento as propõe, voltadas para a construção do senso crítico deles, especialmente no que se refere ao ensino das funções trigonométricas, avaliando as metodologias adequadas que viabilizem o desenvolvimento da habilidade citada para resolução de problemas que envolvam fenômenos periódicos.
Metodologias ativas
Ao longo da BNCC, termos como “resolução de problemas” e “relacionar a teoria com a prática” aparecem como direcionamentos para as aulas de Matemática do Novo Ensino Médio. Existem algumas indicações de como os professores devem planejar e organizar suas aulas de acordo com o novo cenário da Educação. No atual cenário mundial, reconhecer-se em seu contexto histórico e cultural, comunicar-se, ser criativo, analítico-crítico, participativo, aberto ao novo, colaborativo, resiliente, produtivo e responsável requer muito mais do que o acúmulo de informações (Brasil, 2018, p. 14).
A busca pela promoção do estudante como protagonista do seu processo de ensino-aprendizagem, desafia os professores na convergência das metodologias a serem empregadas e no plano de aula. Para tornar o caminho possível em sala de aula, as metodologias ativas aparecem com uma alternativa de abordagem que valoriza a autonomia do estudante.
Para Viegas (2019, p. 1), as metodologias ativas consistem na mudança do paradigma do aprendizado e da relação entre o aluno e o professor. O aluno passa a ser o protagonista e o agente transformador do processo de ensino, enquanto o educador assume o papel de orientador, abrindo espaço para a interação e a participação dos estudantes na construção do conhecimento.
Dentre as metodologias ativas conhecidas, existe a Problem Based Learning (PBL) ou a Aprendizagem Baseada em Problemas, metodologia baseada na aprendizagem decorrente de problemas para iniciar, enfocar e motivar à aprendizagem de um conteúdo a ser trabalhado, contemplado no plano de aula, podendo ser desenvolvido de forma individual ou em pares.
A PBL surgiu na década de 1960, na Universidade McMaster, no Canadá. A iniciativa de uma mudança curricular partiu da constatação de que os egressos de Medicina deixavam o curso com baixa capacidade para aplicar os conteúdos conceituais na realização de diagnósticos e com poucas habilidades e atitudes profissionais desejáveis à prática médica (Ribeiro, 2008, p. 32). A literatura destaca algumas vantagens dos métodos que pressupõem que a aprendizagem é aprimorada pela interação social e facilitada quando os estudantes são expostos a situações da vida real (Ribeiro, 2008, p. 34).
O método consiste em apresentar aos alunos situações motivadoras e problemas da vida real que devem ser resolvidos com autonomia, engajamento e senso crítico. O objetivo está em alcançar a percepção e a correlação entre as teorias existentes a fim de solucionar os problemas. O método, portanto, vai ao encontro do que a BNCC propõe para o Novo Ensino Médio.
Metodologia
Esta investigação foi realizada com 90 alunos matriculados no terceiro trimestre da 2ª série do Ensino Médio de uma escola particular do Distrito Federal, no período de 20 de setembro a 20 de outubro de 2021. Divididos em duas turmas, A e B (sendo a turma A presencial e a turma B online), oito encontros foram realizados em horários semanais, totalizando uma carga horária de 8h40min. Os próprios autores deste artigo foram os investigadores e desenvolvedores das oficinas. Essa investigação seguiu uma abordagem qualitativa, buscando trazer as falas e as percepções dos estudantes, assim como os registros das imagens das atividades desenvolvidas.
Com a finalidade de avaliar na prática as experiências proporcionadas pelas metodologias ativas de ensino, a pesquisa consistiu em iniciar o estudo das funções trigonométricas, adotando a abordagem proposta pela metodologia PBL. O intuito era instigar os alunos à reflexão a partir de um problema inicial envolvendo o fenômeno periódico da altura de uma maré em determinado tempo. Uma vez exposto o problema, os alunos foram convidados a pensar a respeito e a apresentar possíveis soluções, de modo que, nesse processo, as ideias convergem para o conceito de função trigonométrica por meio da construção de um gráfico dos pontos encontrados pelos estudantes.
Foi apresentada a função 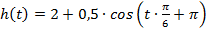 , em que h representa a altura da maré, em metros, e t o tempo, em horas. Os alunos precisavam calcular a altura da maré em determinados horários para, então, observarem as repetições que caracterizam as funções trigonométricas, tentando justificar o fenômeno da repetição.
, em que h representa a altura da maré, em metros, e t o tempo, em horas. Os alunos precisavam calcular a altura da maré em determinados horários para, então, observarem as repetições que caracterizam as funções trigonométricas, tentando justificar o fenômeno da repetição.
A pesquisa consistiu, portanto, nas seguintes etapas: 1) apresentação do problema; 2) espaço para reflexões e discussões; 3) formalização do conceito de função trigonométrica e seus parâmetros; 4) observação do comportamento gráfico utilizando o software Geogebra em iPads fornecidos pela instituição para cada estudante; 5) resolução de exercícios do livro didático adotado pela escola.
Resultados
No primeiro encontro, foi proposto o problema às turmas para que os estudantes pudessem construir o conceito inicial das funções trigonométricas. Na turma A (presencial), o trabalho foi desenvolvido de forma individual, devido ao protocolo de distanciamento da instituição. Na turma B, o desenvolvimento deu-se com a formação de duplas, utilizando a plataforma Microsoft Teams.
O objetivo do primeiro encontro era estabelecer o protagonismo do estudante, sem a intervenção do professor para que pudessem responder ao problema inicial e constituir as principais características das funções trigonométricas. A figura 1 apresenta as respostas de um estudante da turma B, enviada pelo chat do Teams. A figura 2 mostra uma estudante da turma A realizando as atividades:
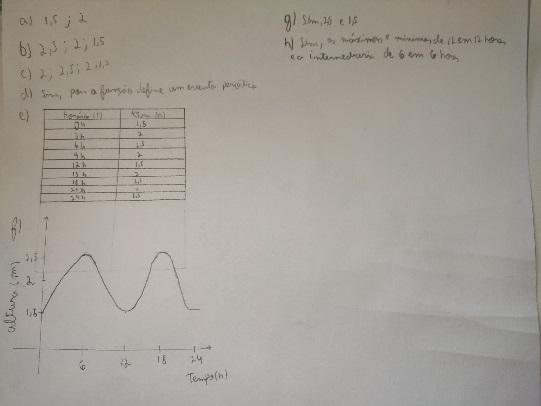
Figura 1: Respostas de um estudante da turma B

Figura 2: Estudante da turma A realizando a atividade
O segundo encontro foi voltado à escuta e ao registro dos resultados encontrados pelos estudantes, por meio de uma mediação necessária. Neste momento, algumas falas dos estudantes chamaram a atenção, pois uma estudante pensou na seguinte hipótese:
Professor, calculei h (0) e encontrei 1,5m, h (3) e encontrei 2m, h (6) e encontrei 2,5m, então h (9) vai ser 3m e vai aumentando de 0,5m (Estudante 1).
Em seguida, um estudante rebateu a afirmação anterior:
Resolvi h (9) e encontrei 2m e os valores não vão aumentando de 0,5 em 0,5 (Estudante 2).
Enquanto outra estudante acrescentou:
Professor percebi que os valores aumentam, diminuem e se repetem (Estudante 3).
No terceiro encontro, foi realizada uma formalização da função seno e função cosseno, mostrando a definição, os elementos, os parâmetros, as características e os meios para encontrar os valores máximos e os valores mínimos das funções e dos seus períodos.
No quarto encontro, foi trabalhada a construção gráfica. Neste momento, foram distribuídos iPads para os estudantes (Figura 3), com o objetivo de que, por meio da utilização do software Geogebra, percebessem as transformações sofridas pelos gráficos em decorrência da variação de seus parâmetros.

Figura 3: Estudante utilizando o Geogebra no iPad
Nos demais encontros foi feita a resolução e a correção de atividades do livro didático adotado pela instituição de ensino.
Conclusão
Desde o primeiro encontro, ficou evidente um melhor desempenho da turma B, na qual a atividade foi realizada em dupla. Na turma A, alguns estudantes não conseguiram desenvolver o raciocínio para a resolução do problema. Aparentemente, sentiam-se inseguros para a realização individual da tarefa. Apesar de o desenvolvimento ter ocorrido de forma distinta para as duas turmas, a metodologia ativa funcionou bem para ambas. Importante destacar que os resultados apresentados pelos alunos tiveram maior êxito quando a atividade foi realizada em dupla.
Conforme as experiências dos autores deste artigo, nos últimos cinco anos foi possível observar que a percepção dos estudantes sobre as discussões mediadas deu resultados positivos, tendo em vista a sua compreensão empírica sobre o comportamento das funções trigonométricas, especialmente em relação à repetição periódica. Quando comparada à forma tradicional de ensino - na qual a função é apresentada antes das aplicações - a metodologia ativa torna-se mais adequada, pois a resiliência envolvida, no processo de o estudante ser o protagonista, atenua a dificuldade dos alunos com as abstrações matemáticas.
Vale destacar que o apoio tecnológico foi muito importante para que os estudantes percebessem a construção gráfica e as mudanças no gráfico a partir da alteração de cada parâmetro.
A análise dos resultados nos permitiu concluir que a utilização da metodologia ativa adotada pode refletir uma melhoria no entendimento inicial do conteúdo e no desenvolvimento das atividades. Os estudantes mostraram-se mais motivados em assumir um protagonismo nas suas próprias trilhas de aprendizagem e perceberam que podem aprender a aprender, especialmente de forma conjunta, obtendo êxito no desenvolvimento da habilidade EM13MAT306, da BNCC, relacionada ao ensino das funções trigonométricas (Brasil, 2018, p. 536).
Referências
BALDEZ, Alda; DIESEL, Aline; MARTINS, Silvana. Os princípios das metodologias ativas de ensino: uma abordagem teórica. Revista Thema, Lajeado, v. 14, nº 1, p. 268-288, 2017.
BERBEL, Neusi. As metodologias ativas e a promoção da autonomia dos estudantes. Seminário: Ciências Sociais e Humanas, Londrina, v. 32, nº 1, p. 25-40, 2011.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC, 2018.
DISTRITO FEDERAL. Secretaria de Estado de Educação. Currículo em Movimento do Distrito Federal – Ensino Fundamental: anos iniciais. Brasília: SEE, 2018.
______. Currículo em Movimento do Distrito Federal – Ensino Médio. Brasília: SEE, 2018.
IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David; PÉRIGO, Roberto; ALMEIDA, Nilze. Matemática – ciência e aplicações. 9ª ed. São Paulo: Saraiva, 2016.
RIBEIRO, L. R. C. Aprendizagem Baseada em Problemas: uma experiência no Ensino Superior. São Carlos: Edufscar, 2008.
SOPELSA, Oliveira; GAZZÓLA, Lucivani; DETONI, Marilena Zanoello. Os desafios do ensino e da aprendizagem na Matemática no contexto histórico-cultural e a constituição dos saberes docentes. X ANPED SUL, Florianópolis, outubro de 2014.
VIEGAS, Amanda. Metodologias ativas: como essa tendência pode beneficiar as práticas pedagógicas? Plataforma Educacional, 2019. Disponível em: https://www.somospar.com.br/metodologias-ativas-como-essa-tendencia-pode-beneficiar-as-praticas-pedagogicas. Acesso em: 27 ago. 2021.
Publicado em 26 de abril de 2022
Como citar este artigo (ABNT)
TAVARES, Juliana Abrantes; SIMÕES, Leonardo Henrique Santos; BEZERRA, Wescley Well Vicente; EVANGELISTA, Tatiane da Silva. O uso de metodologias ativas no ensino das funções trigonométricas: uma adequação para o novo Ensino Médio. Revista Educação Pública, Rio de Janeiro, v. 22, nº 15, 26 de abril de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/15/o-uso-de-metodologias-ativas-no-ensino-das-funcoes-trigonometricas-uma-adequacao-para-o-novo-ensino-medio
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

