Aplicação do método de indução matemática no Ensino Médio com o estudo das sequências de números poligonais
Janiely Lima da Silva
Aluna do Ensino Médio no IFRN - Câmpus São Paulo do Potengi
Luzia Clênia Campos da Costa
Aluna do Ensino Médio no IFRN - Câmpus São Paulo do Potengi
Maria Luana Domingos de Oliveira
Aluna do Ensino Médio no IFRN - Câmpus São Paulo do Potengi
Oscar Bezerra Dantas
Aluno do Ensino Médio no IFRN - Câmpus São Paulo do Potengi
Josimar José dos Santos
Docente no IFRN - Câmpus Natal – Zona Norte
Indução, segundo o Dicionário Aurélio, é a ação de induzir, de ser a razão de algo ou de ter a capacidade de provocar algo. É o ato de fazer com que alguém acredite ou passe a acreditar em alguma coisa. Mas, dependendo da área de conhecimento em que a palavra é empregada, as intenções e interpretações podem e vão ser diferentes, por ser observada de pontos de vista distintos e com diversas finalidades. A origem etimológica da palavra indução, segundo o site Significados, é no latim inductio, que, ao ser traduzido, significa “ação de levar e trazer” ou “ação de introduzir”. Também é mencionado no site que Francis Bacon (1551-1627), responsável pelo método experimental, proporcionou a partir do método indutivo que o homem despertasse em si o desejo pela experiência e pelo que é concreto, fazendo com que houvesse maior necessidade de comprovar determinados fenômenos.
Na Matemática não é possível afirmar que determinadas fórmulas são verdadeiras até que sejam provadas a partir de um artifício de comprovação. A indução matemática, assunto que será tratado no presente trabalho, é um método utilizado para demonstrar a veracidade de um dado número que tem propriedade e que seu sucessor também a possui, e assim sucessivamente. Existe uma analogia entre o princípio de indução matemática a uma fileira infinita de dominós no qual se leva em consideração dois questionamentos:
i) O que ocorre se derrubarmos o 1° dominó? ii) E se o 7° for derrubado? Esperamos no item (i) que os alunos aceitem com razoável facilidade que todos os dominós realmente irão cair. Já no item (ii), espera-se que os alunos considerem que todos os dominós depois do sétimo (e o sétimo inclusive) sejam derrubados (Nóbrega, 2013, p. 6).
Para um entendimento mais claro, passamos a descrever o princípio de indução matemática. Seja P(n) uma asserção sobre os números naturais; verifica-se que: i) P(1) é verdadeira; ii) Sempre que P(n) for verdadeira, para algum n pertencente aos naturais, implica que
P(n + 1) também é verdadeira, então conclui-se que P(n) é verdadeira para todo n natural.
Para a produção do presente trabalho, consultamos as dissertações de mestrado de Santos (2013) e Nóbrega (2013), cujo objetivo principal é apresentar o princípio de indução matemática para estudantes do Ensino Médio a partir de atividades que focam em demonstrações. Esses autores enfatizam a importância de trabalhar o método de indução matemática no ambiente escolar como meio de despertar a curiosidade e o interesse pela Matemática.
Este trabalho aborda como introduzir o método de indução matemática no Ensino Médio. Para isso, utilizamos as sequências de números poligonais, que é um conjunto de pontos organizados de modo a formar polígonos regulares. As sequências são classificadas de acordo com a quantidade de lados do polígono. Por exemplo: se o polígono possui três lados, temos a sequência dos números poligonais triangulares; se o polígono possuir quatro lados, temos a sequência dos números poligonais quadrangulares, e assim sucessivamente. Para melhor compreensão, trazemos a Figura 1.
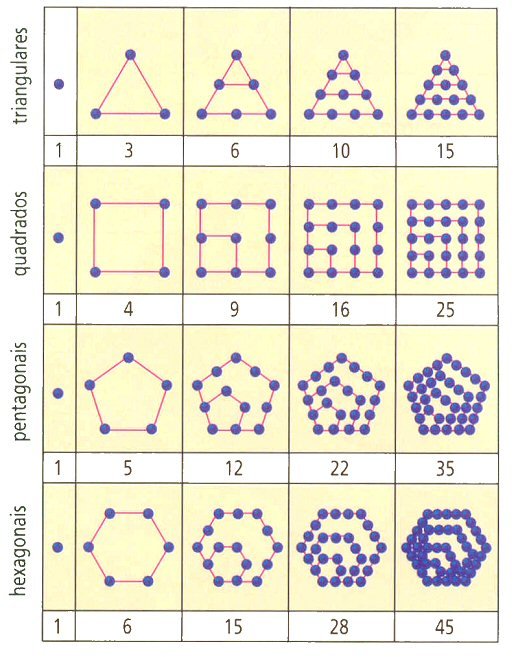
Figura 1: Números poligonais
Fonte: http://obviousmag.org/archives/uploads/2006/060825_series.jpg
O trabalho foi realizado em duas etapas: a primeira consistiu em conjecturar fórmulas a partir de observações dessas sequências. Na segunda etapa foi apresentado o método de indução matemática e, com base nele, foram provadas as conjecturas obtidas na etapa anterior.
Acreditamos que este trabalho também pode auxiliar professores da área a buscar uma forma de ministrar esse conteúdo de maneira simples e prática.
Fundamentação teórica
A indução matemática é uma das técnicas de demonstração mais importantes para verificação de conjecturas de propriedades referentes aos números naturais. Esse método de indução se distingue dos princípios indutivos usados em outras ciências, como por exemplo, nas Ciências Biológicas, que usam um tipo de método de indução para deduzir as variáveis envolvidas em um determinado fenômeno. O método da indução nas Ciências Biológicas é desenvolvido a partir da observação de casos particulares e tem como finalidade obter uma generalização (lei geral ou universal), diferentemente do que ocorre na indução matemática, em que não é possível fazer generalizações com base em observações de casos particulares.
O método foi criado por contribuições de diversos matemáticos, mas, segundo Morgado (1990, apudSantos, 2011), o termo “indução matemática” é considerado mais recente e atribuído a Augustus Morgan em 1838, além de ter sido citado por outros matemáticos renomados. Santos (2011) destaca ainda que, ao longo dos anos, a ideia de indução foi tema de debate e oposição aos sofistas. A partir desses acontecimentos surgiu o conceito de indução, criado por Aristóteles (384-322 a.C.), na Grécia. Porém, o conceito apresentado pelo filósofo não se disseminou na cultura grega.
De acordo com Santos (2011), após isso surgiram outros conceitos para esse método demonstrativo, com a contribuição de autores como: Francis Bacon (1561-1627), David Hume (1711-1756) e Stuart Mill (1806-1873).
A concepção do conceito do método indutivo, tomou como base os axiomas de Peano (Santos, 2011), propostos em 1899, considerando os parâmetros aritméticos, os quais formalizavam a noção de que todos os números naturais podem ser obtidos a partir do número 1 pela soma sucessiva da unidade.
A indução matemática é uma importante ferramenta e possui papel fundamental no desenvolvimento, através da prática, das capacidades analíticas do estudante. É um método de demonstração utilizado para provar que certas propriedades são verdadeiras para todos os números naturais. Essa ideia é corroborada por Lima (1998 apud Santos, 2013, p. 18) quando destaca que
o princípio da indução matemática é um eficiente instrumento para a demonstração de fatos referentes aos números naturais. Por isso deve-se adquirir prática em sua utilização. Por outro lado, é importante também conhecer seu significado e sua posição dentro do arcabouço da Matemática. Entender o princípio da indução é praticamente o mesmo que entender os números naturais.
Entretanto, segundo Santos (2013), em virtude da forma como a Matemática é vista atualmente nas escolas, ou seja, voltada apenas para fórmulas prontas e métodos de resolução de problemas, a introdução desse método de demonstração não é feita na grade curricular dos estudantes do Ensino Médio. Nóbrega (2013) ratifica a ideia de Santos (2013) quando traz em seu trabalho um meio para lecionar o método de indução matemática para estudantes do 1º ano do Ensino Médio, destacando sua importância e viabilidade para que haja estimulação e formulação de conjecturas e a ratificação por meio da indução matemática.
No entanto, com base no ensino atual, é notória a necessidade de um ensino menos preocupado com resultados já prontos e mais voltado para o desenvolvimento de um pensamento crítico, no qual o estudante se torna capaz de desenvolver argumentos que validam seu pensamento analítico. Nesse sentido, percebe-se que o desenvolvimento do pensamento crítico se apresenta de modo muito relevante, para os alunos, no processo de ensino-aprendizagem, pois, além de contribuir para a formação acadêmica dos discentes, segundo Marani et al. (2019), auxilia na formação do cidadão e de sua atuação ativa na sociedade. Essa ideia é ratificada por Santos (2013, p. 12) quando enfatiza que é necessário enxergar
a necessidade de um ensino menos preocupado com resultados e mais voltado para o processo onde se trabalha tanto a capacidade de abstração do aluno quanto o pensamento analítico. Ao trabalhar o processo, o aluno desenvolve a capacidade de criar sequências lógicas e assim analisar situações e tirar conclusões, podendo essas situações ser matemáticas ou não (Santos, 2013, p. 12).
Diante dos fatos elencados, compreende-se a importância de trabalhar métodos de demonstração no ensino básico, pois proporciona ao discente uma visão mais lógica perante resultados encontrados, incentivando-o a compreender o raciocínio utilizado para resolver problemas, possibilitando, assim, uma maior segurança na obtenção e consolidação do conhecimento matemático. No entanto, para isso ocorrer é necessário que a maneira como as demonstrações são apresentadas aos futuros professores em sua formação acadêmica seja revista, a fim de que obtenha segurança no uso das técnicas de demonstrações. Essa ideia é destacada por Santos (2013, p. 13) quando afirma que
o futuro professor é apresentado de uma forma equivocada ao mundo das provas e demonstrações, o que causa uma impressão de que demonstração é algo complicado, e se é complicado para o professor, é complicado para o aluno, o que leva os professores a terem receios de levar demonstrações aos alunos.
Acreditamos que é necessária a mudança da postura do professor perante as demonstrações, para que sejam trabalhadas essas técnicas com os discentes de forma mais simples e segura.
Metodologia
Este trabalho é uma aplicação de pesquisa bibliográfica, que, segundo Gil (2002, p.44), “é desenvolvida com base em material já elaborado, constituído principalmente de livros e artigos científicos”. Nesse sentido, buscamos em artigos científicos e dissertações de mestrado argumentos para fundamentar a aplicação do método de indução matemática em turmas do Ensino Médio.
Com o propósito de atender aos objetivos propostos pelo professor, o ano letivo de 2019 foi iniciado com o assunto de sequências numéricas: sequência aritmética e sequência geométrica. Em decorrência disso, foi proposto pelo docente um desafio sobre os números poligonais para que a turma determinasse a quantidade de pontos na 20ª figura de cada sequência. Para isso, foi necessário desenvolver uma fórmula recursiva, uma fórmula iterada e uma fórmula fechada a partir dos dados fornecidos. Após a resolução do problema por quatros discentes, o professor fez o convite aos demais para estudar o método de indução matemática. Em seguida, ocorreram encontros para debater o método e aplicá-lo como forma de comprovar a veracidade das fórmulas encontradas.
Destaca-se aqui que a atividade foi desenvolvida em sala de aula pelo docente para as sequências de números poligonais triangulares e quadrangulares.
Desafios com os números poligonais pentagonais, hexagonais e heptagonais
Para a realização do desafio com os números poligonais (pentagonais, hexagonais e heptagonais), adotaram-se as etapas relacionadas a seguir com a finalidade de obter o resultado que foi proposto.
Observou-se que os números de elementos (pontos) de cada figura formam uma sequência; a partir disso, pôde-se desenvolver a primeira etapa, que se refere aos números poligonais pentagonais.
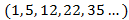
Analisando cada figura, a quantidade de elementos e sua posição, temos que:
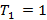
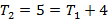
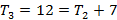
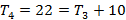
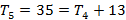
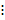
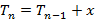
Analisando essa sequência, percebe-se que cada termo a partir do segundo é a soma do termo anterior com o acréscimo de determinado número. Observou-se também que o termo 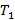 , junto com os números que foram acrescentados, forma uma progressão aritmética (PA):
, junto com os números que foram acrescentados, forma uma progressão aritmética (PA):
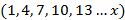
Para obter a fórmula recursiva, precisamos determinar o valor de x. Segue dessa PA que:
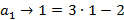
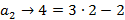
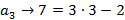
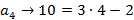
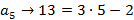
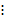
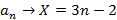
Portanto, 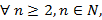 a fórmula recursiva para os números pentagonais, é:
a fórmula recursiva para os números pentagonais, é:
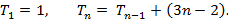
Em seguida, determinamos a fórmula iterada a partir da fórmula recursiva. Para isso, a partir do segundo termo substituímos o termo anterior ao termo seguinte sem realizar a soma. Veja o exemplo abaixo:
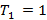
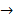
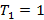
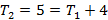
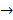
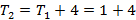
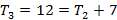
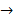
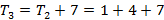
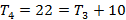
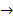
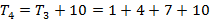
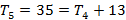
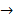
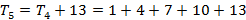
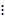
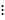
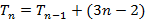
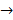
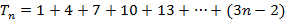
Portanto, 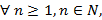 a fórmula iterada para os números pentagonais é:
a fórmula iterada para os números pentagonais é:
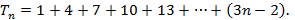
Por último, obtemos a fórmula fechada. Observou-se que o termo 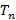 da forma iterada forma os termos da PA:
da forma iterada forma os termos da PA:
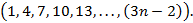
A partir dessa PA é possível descobrir a fórmula fechada da sequência dos números poligonais pentagonais, o qual nos permite obter o número de pontos de uma figura em uma posição qualquer. Com o propósito de obter a fórmula fechada, usamos a fórmula da soma dos 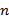 primeiros termos de uma PA. Assim, encontraremos:
primeiros termos de uma PA. Assim, encontraremos:
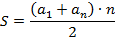
Temos que 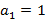 e o
e o 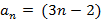 , e substituindo obtém-se:
, e substituindo obtém-se:
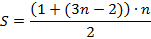
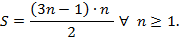
A partir dessa fórmula (fechada), é possível descobrir a quantidade de pontos em qualquer termo da sequência dos números poligonais pentagonais.
Resolvendo o desafio para os números poligonais pentagonais, encontraremos a quantidade de pontos para a vigésima figura. Fazendo 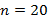 e substituindo na fórmula acima, temos:
e substituindo na fórmula acima, temos:
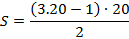
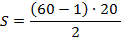
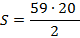
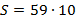
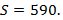
Logo, a vigésima figura será constituída por 590 pontos.
Seguindo o mesmo raciocínio com as etapas já apresentadas, tem-se a possibilidade de obter as fórmulas recursiva, iterada e fechada para as demais sequências de números poligonais (hexagonais e heptagonais). A partir desses resultados, podemos encontrar a quantidade de pontos da 20ª figura das respectivas sequências.
Para a sequência dos números poligonais hexagonais temos:
Fórmula recursiva: 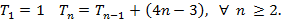
Fórmula iterada: 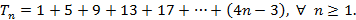
Fórmula fechada: 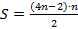 ,
, 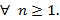
Fazendo 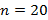 e substituindo na fórmula fechada, temos:
e substituindo na fórmula fechada, temos:
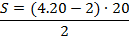
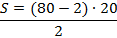
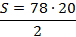
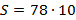
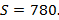
Logo, a vigésima figura da sequência dos números poligonais hexagonais será constituída por 780 pontos.
Para a sequência dos números poligonais heptagonais temos:
Fórmula recursiva: 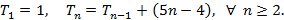
Fórmula iterada: 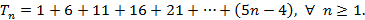
Fórmula fechada: 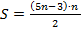 ,
, 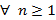 .
.
Fazendo 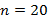 e substituindo na fórmula fechada, temos:
e substituindo na fórmula fechada, temos:
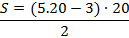
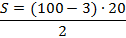
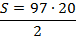
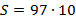
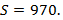
Logo, a vigésima figura da sequência dos números poligonais heptagonais será constituída por 970 pontos.
Prova por indução da sequência dos números poligonais pentagonais, hexagonais e heptagonais
Neste momento descrevemos a verificação da validade das fórmulas obtidas anteriormente usando o método de indução matemática. Para isso, vamos fazer a demonstração da validade da fórmula fechada para a sequência de números poligonais pentagonais. Seja 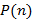 a seguinte proposição:
a seguinte proposição:
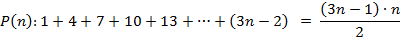
A primeira etapa consiste na comprovação de que 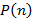 é verdadeira para
é verdadeira para 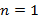 , isto é, vamos verificar que
, isto é, vamos verificar que 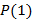 é verdadeira. Assim,
é verdadeira. Assim,
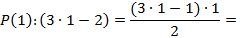
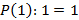
Como a primeira figura da sequência dos números poligonais pentagonais tem um ponto, então está provado que 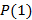 é verdadeira. Supondo agora que
é verdadeira. Supondo agora que 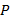 é verdadeiro para algum número natural
é verdadeiro para algum número natural 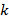 , temos assim nossa hipótese de indução:
, temos assim nossa hipótese de indução:
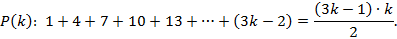
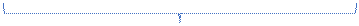
Hipotese de indução
Vamos verificar que 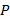 também é verdade para
também é verdade para 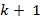 . Assim:
. Assim:
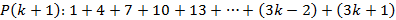
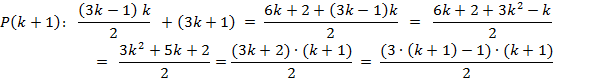
Observe que 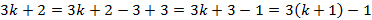 . Como verificamos que a propriedade é verdadeira para
. Como verificamos que a propriedade é verdadeira para 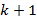 , então conclui-se, pelo método de indução, que a propriedade é verdadeira para todos os números naturais.
, então conclui-se, pelo método de indução, que a propriedade é verdadeira para todos os números naturais.
Seguindo o mesmo raciocínio, verifica-se por indução que as fórmulas obtidas para outras sequências também são verdadeiras.
Considerações finais
A partir do desenvolvimento deste trabalho, verificou-se a importância da aplicação do método indutivo na aprendizagem da Matemática no Ensino Médio, pois com esse método é possível construir uma linha de raciocínio perante os problemas matemáticos sem dar enfoque aos resultados prontos, mas sim às possibilidades para encontrá-los.
Sabe-se que esse conteúdo é abordado nos cursos de graduação em Matemática como uma técnica de demonstração de propriedades referentes aos números naturais. Acreditamos que a prática e o estudo desse método possibilitam e estimulam o domínio do conteúdo, podendo ser aplicados de acordo com as séries do Ensino Fundamental e Médio, ampliando habilidades por meio das observações e formulação de conjecturas.
O trabalho realizado foi de grande satisfação para os envolvidos, pois a partir dele despertou-se o interesse na compreensão do universo da Matemática. Por outro lado, percebeu-se que uma parcela muito pequena dos integrantes da turma concluiu a fase inicial proposta. Tal situação pode ser justificada pelo fato de a Matemática ser considerada uma matéria difícil e, além disso, não ser prioridade para os alunos que possuem dificuldades. Entretanto, a indução contribuiu bastante para a aprendizagem dos discentes que se dispuseram a participar.
Para finalizar, enfatizamos que com planejamento é possível trabalhar esse e até outros conteúdos no Ensino Médio; para isso ocorrer, é necessário o uso de estratégias para a realização da turma como um todo.
Referências
GIL, Antônio Carlos. Como classificar as pesquisas? O que é pesquisa bibliográfica? In: ______. Como elaborar projetos de pesquisa. 4ª ed. São Paulo: Atlas, 2002. p. 1-176. Disponível em: http://www.uece.br/nucleodelinguasitaperi/dmdocuments/gil_como_elaborar_projeto_de_pesquisa.pdf. Acesso em: 12 ago. 2020.
INDUÇÃO (verbete). DICIO, Dicionário Online de Português. Porto: 7Graus, 2020. Disponível em: https://www.dicio.com.br/inducao/#:~:text=Significado%20de%20Indu%C3%A7%C3%A3o,de%20provocar%20alguma%20coisa%3B%20instiga%C3%A7%C3%A3o. Acesso em: 16 maio 2020.
INDUÇÃO. Significados. Porto: 7Graus, 2020. Disponível em: https://www.significados.com.br/inducao/#:~:text=Mas%2C%20a%20palavra%20indu%C3%A7%C3%A3o%20pode,ou%20%E2%80%9Ca%C3%A7%C3%A3o%20de%20introduzir%E2%80%9D. Acesso em: 30 maio 2021.
MARANI, Pamela Franco et al. Desenvolvimento do pensamento crítico no ensino de Ciências: publicações em eventos nacionais. Scientia Naturalis, Rio Branco, v. 1, nº 2, p. 69-82, 2019. Disponível em: https://periodicos.ufac.br/index.php/SciNat/article/view/2494 . Acesso em: 10 jul. 2020.
MATEMÁTICA DISCRETA. Indução matemática. Disponível em: https://pt.m.wikiversity.org/wiki/Matem%C3%A1tica_Discreta/Indu%C3%A7%C3%A3o_matem%C3%A1tica . Acesso em: 16 maio 2020.
MÉTODO INDUTIVO. Significados. Porto: 7Graus, 2020. Disponível em: https://www.significados.com.br/metodo-indutivo/ . Acesso em: 16 maio 2020.
NÓBREGA, Luciano Xavier Gomes da. Princípio da indução matemática no Ensino Médio. 2013. 61f. Dissertação (Mestrado em Matemática) – Universidade Federal do Rio Grande do Norte, Natal, 2013. Disponível em: https://repositorio.ufrn.br/handle/123456789/17018 . Acesso em: 12 maio 2020.
SANTOS, Anderson Carvalho dos. O uso de demonstrações no ambiente escolar a partir do princípio de indução finita. 2013. 52f. Dissertação (Mestrado) - Instituto Nacional de Matemática Pura e Aplicada, Rio de Janeiro, 2013. Disponível em: https://impa.br/wp-content/uploads/2016/12/anderson_carvalho.pdf . Acesso em: 12 maio 2020.
SANTOS, Graça Luiza Dominguez. Aspectos da Indução, nas Ciências e na Matemática. s/d. Disponível em: https://www.academia.edu/3557691/Aspectos_da_Indu%C3%A7%C3%A3o_nas_Ci%C3%AAncias_e_na_Matem%C3%A1tica. Acesso em: 25 out. 2019.
Publicado em 07 de junho de 2022
Como citar este artigo (ABNT)
SILVA, Janiely Lima da; COSTA, Luzia Clênia Campos da; OLIVEIRA, Maria Luana Domingos de; DANTAS, Oscar Bezerra; SANTOS, Josimar José dos. Aplicação do método de indução matemática no Ensino Médio com o estudo das sequências de números poligonais. Revista Educação Pública, Rio de Janeiro, v. 22, nº 21, 7 de junho de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/21/aplicacao-do-metodo-de-inducao-matematica-no-ensino-medio-com-o-estudo-das-sequencias-de-numeros-poligonais
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

