O uso do Winplot como software educativo no ensino da função quadrática
Janailson Silva Marinho
Professor de Matemática na rede pública da Paraíba, graduado em Matemática (UEPB - Câmpus Campina Grande), pós-graduando em Ensino de Ciências e Matemática (UAB/IFPB)
Quando pensamos no ensino da Matemática, o que vem em mente são os desafios e as possibilidades que, possivelmente, surgirão durante o processo de ensino. Para a grande maioria das pessoas, estudar Matemática torna-se uma tarefa desafiadora, não só para quem irá ser o ouvinte, mas também para aqueles que a lecionam.
Sabemos que a utilização do material tecnológico, em sala de aula, influencia na aprendizagem dos alunos, favorecendo o desenvolvimento do raciocínio lógico, a rapidez no pensamento dedutivo, a socialização, a organização do pensamento e a concentração. O material é necessário tanto para a compreensão, como para a resolução de problemas matemáticos. Modrow e Silva (2013, p. 10), escrevendo sobre os desafios a serem superados, destacam:
A presença das TIC nas escolas proporciona aos professores novas formas de ensinar, de modo a oportunizar uma aprendizagem mais significativa aos alunos, visto que estes vivem num ambiente informatizado, fator que pode influenciar no seu pensamento e na sua imaginação.
É nesse sentido que buscamos apresentar o software Winplot como recurso didático no ensino da função quadrática. Ele oferece subsídios para uma melhor aprendizagem, pois, por meio de imagens, desenvolve a percepção e a clareza do raciocínio, além de possibilitar maior participação dos alunos.
Nessa perspectiva, surge a seguinte questão problema: quais as principais contribuições e os desafios do software Winplot no ensino da função quadrática?
Trata-se, portanto, de uma pesquisa bibliográfica com abordagem qualitativa com o objetivo principal de apresentar as principais contribuições e desafios do software Winplot no ensino da função quadrática.
Os argumentos para responder à questão problema foram produzidos a partir das contribuições dos estudos de autores como Sousa, Lins e Abreu (2016), Valentim (2014), Oliveira e Pereira (2013), entre outros.
O Winplot, por se tratar de um programa leve e de fácil acesso, torna-se uma ferramenta altamente viável para o ensino da Matemática, favorecendo um bom desempenho no ensino-aprendizagem. Parte dessa pesquisa buscou explorar alguns recursos básicos oferecidos no software, no qual foi possível perceber a variação dos coeficientes de uma mesma função pré-definida, analisando as relações entre seus gráficos e coeficientes.
Portanto, esse trabalho organiza-se numa sequência lógica. Além da presente introdução, há uma seção teórica, sobre a qual se realizou um breve levantamento histórico das funções, apresentando algumas importantes contribuições do Winplot. Além disso, discutimos sobre a utilização do referido software no ensino da função quadrática e construímos uma seção metodológica onde é descrito o tipo da pesquisa, como também o passo a passo de como foi desenvolvido este trabalho.
O software Winplot
Desenvolvido em 1985 por Richard Parris, da Philips Exeter Academy, é um software gráfico de usos múltiplos. Na época, ele era executado no DOS (sistema operacional em disco) e se chamava Plot. Com o surgimento do ambiente operacional Windows, o programa passou a ser chamado de Winplot. Foi traduzido para o português por Adelmo Ribeiro de Jesus. Agora, o software encontra-se disponível em mais de dez idiomas. Sua principal função é desenhar gráficos de funções de uma ou duas variáveis, porém executa ainda vários outros comandos.
Breve histórico do conceito de função e as contribuições do Winplot
O conceito de função foi muito discutido e avaliado pelos estudiosos ao longo da história. Iezzi et al. (2004) afirmam que o conceito de função não foi formulado de modo satisfatório antes do século XIX, mas aparece de forma implícita em várias situações na Matemática da Antiguidade. O matemático alemão G.W Leibniz (1646-1716), na metade do século XVII, usou a palavra “função” pela primeira vez para indicar uma quantidade geométrica variável de um ponto a outro de uma curva (Iezzi et al., 2004).
Palavras como variável, constante e parâmetros devem-se também a Leibniz. Já a notação 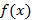 , que indica uma função, só foi introduzida em 1734 pelo ilustre matemático suíço, Leonhard Euler (Iezzi et al., 2004). Euler enfatizou, como conceito de função, que toda variável depende de outra. Seus estudos foram essenciais para o desenvolvimento do conceito de funções, trazendo grandes contribuições para as notações e a linguagem simbólica que utilizamos hoje.
, que indica uma função, só foi introduzida em 1734 pelo ilustre matemático suíço, Leonhard Euler (Iezzi et al., 2004). Euler enfatizou, como conceito de função, que toda variável depende de outra. Seus estudos foram essenciais para o desenvolvimento do conceito de funções, trazendo grandes contribuições para as notações e a linguagem simbólica que utilizamos hoje.
Nicole Oresme (1325-1282) expôs seu método para representar geometricamente fenômenos de uma variável numa obra publicada, em 1350, e foi a partir daí que surgiram os primeiros gráficos. As coordenadas (eixos do plano cartesiano) que entendemos hoje como abscissas e ordenadas, antes eram conhecidas como as latitudes e longitudes de Oresme (Iezzi et al., 2004).
Percebe-se, pois, que não foi fácil a construção do conceito de função e que há certa complexidade no entendimento de tal conceito. Logo é necessário aprimorarmos nossas práticas de ensino para que o estudo de função possa ser simplificado, contribuindo para uma melhor compreensão e, consequentemente, obtermos uma aprendizagem significativa. No tocante aos gráficos das funções, é preciso explanar a respeito, de forma clara e objetiva, para que haja de fato um entendimento de cada elemento nele contido. A dificuldade para uma boa explanação torna-se evidente em uma aula tradicional, pois dificilmente a construção de um gráfico de uma função quadrática, utilizando apenas lápis, régua e o quadro branco, resultará em um gráfico perfeito. Entretanto, a tecnologia surge de forma positiva, proporcionando novos métodos de ensino com o intuito de facilitar a aprendizagem. De acordo com Sousa, Lins e Abreu (2016),
o Winplot é uma ferramenta que mostra o gráfico das funções, isto é, apresenta graficamente o comportamento de uma função. É uma ferramenta de grande utilidade que o professor de Matemática pode fazer uso desde o ensino fundamental até o ensino de nível superior. A sua simplicidade e facilidade de utilização, e sua objetividade pode contribuir na aprendizagem do aluno, fazendo com que este visualize melhor o comportamento do gráfico de uma função (Sousa; Lins; Abreu, 2016, p. 6).
Além disso, o software possui animações que possibilitam um melhor entendimento nas variações dos gráficos das funções. Com as animações, o professor poderá explorar outras formas, mais claras e objetivas, de aprendizado. A simplicidade de utilização do software é um ponto positivo que deve ser levado em consideração, visto que o objetivo de uma metodologia é simplificar a compreensão daquilo que está sendo trabalhado. Assim, Sousa, Lins e Abreu (2016, p. 6), escrevendo sobre o manuseio do software relataram:
Diante dessa facilidade de manuseio fica fácil para o professor explicar mais detalhadamente os gráficos gerados pelos diversos tipos de funções. Exige-se, com isso, a utilização de problemas abertos, que estimulem a curiosidade e a busca do resultado pelo aluno, onde ele será capaz de elaborar possíveis soluções para a questão apresentada, e não apenas buscar um resultado.
De fato, ao aplicar o software Winplot para o ensino de funções, observa-se uma aprendizagem mais significativa. Suas contribuições são positivas, tanto para a elaboração e a execução de uma aula, mediada pelo professor, quanto para o interesse e para a aprendizagem dos alunos. Segundo Sousa, Lins e Abreu (2016, p. 2),
o ensino de Matemática por meio das novas tecnologias pode ajudar os docentes a trabalharem suas aulas de forma mais dinâmica e aos discentes pode favorecer uma construção melhor dos conceitos matemáticos, possibilitando uma maneira interativa de ensinar/aprender essa disciplina no contexto escolar.
Verifica-se que o Winplot é um software que possui possibilidades de ensino bem mais atrativas e eficientes. Entretanto, essas possibilidades de ensino acarretam também desafios. Muitos professores, por vários motivos, têm dificuldade de trabalhar com a tecnologia, alguns por falta de recursos e outros por não saberem manusear as ferramentas. Além disso, mesmo aqueles que têm conhecimento do uso das tecnologias, precisam saber como usá-las adequadamente. Logo, é preciso um bom planejamento ou, até mesmo, um bom treinamento para os profissionais da educação, especialmente àqueles que manifestam o interesse de adquirir o preparo para uma boa aula. “Um dos fatores primordiais para a obtenção do sucesso na utilização da informática na educação é a capacitação do professor” (Tajra, 2008, p. 105). Para mais, Jesus e Silva (2015, p. 75) destacam que
o papel do professor é relevante, ele não pode mais permanecer como mero retransmissor de conhecimento. Espera-se dele, nesse novo cenário, capacidade para inovar e estabelecer uma nova relação com os alunos, uma vez que os alunos fazem parte de uma geração mais afeita às tecnologias e mostram-se mais abertos e envolvidos com o seu uso.
Diante disso, entendemos que a tecnologia, por si só, não surte efeito. É preciso haver um empenho sistematizado. Analisando o trabalho desenvolvido por Valentim (2014) é possível perceber que alguns dos professores submetidos à pesquisa, possuíam pouco conhecimento sobre algum software. Cerca de 40% dos professores não tinham conhecimento de nenhum aplicativo e os demais citaram o software GeoGebra. Porém, não houve o registro de professores que utilizavam algum software. Ao serem questionados sobre o que achavam dos softwares, sua utilidade ou não, alguns responderam:
– O momento, o hoje, exige do professor o conhecimento e a habilidade com as novas tecnologias. Podemos dizer que é uma necessidade, porém sua aplicação só dará certo com o domínio do professor sobre o software (P1).
– São recursos valiosos que podemos usar para tornar a aula mais interessante, além de servir como apoio para nós e para o alunado (P2).
– Os softwares matemáticos podem ser úteis no processo ensino-aprendizagem. Porém ainda enfrentamos dificuldades para utilizá-los em sala de aula, já que se faz necessário certo preparo e “familiarização” com cada software (P3) (Valentim, 2014, p. 30).
É compreensível que o ensino de função não seja simples de ser abordado para que os discentes entendam eficazmente. Existem muitos conflitos, tanto no momento do planejamento do professor como no momento da aprendizagem dos alunos. A forma como esse conteúdo é abordado faz toda a diferença para a sua compreensão. Oliveira e Pereira (2013, p. 2), tratando do ensino-aprendizagem dos componentes curriculares da Matemática e da Física no que se refere aos gráficos, relatam:
Uma proposta para minimizar esses conflitos no Ensino-aprendizagem dessas disciplinas, que tem como foco esses conteúdos, é a utilização de softwares que possam facilitar a produção das aulas, criando momentos dinâmicos e diferenciados para o bom entendimento do alunado.
Mesmo reconhecendo a presença da tecnologia, em nosso meio, ainda existe certo receio no meio educacional por parte de alguns docentes para o uso desses recursos. Os professores, que muitas vezes ganham o título daqueles que estão se renovando em busca do conhecimento para simplificar a compreensão dos seus alunos, precisam estar abertos para a descoberta de novos métodos de ensino. E o software Winplot é uma ferramenta que possibilita essa inovação, trazendo contribuições para o ensino, em especial, de função - interpretação gráfica. De acordo com Valentim (2014, p. 42),
através dos estudos realizados e dos dados obtidos na pesquisa, foi possível constatar que o software matemático Winplot é uma ferramenta importante na aprendizagem dos alunos e professores. O uso do software matemático Winplot através da oficina ofertada agregou conhecimentos aos docentes, fazendo-os refletir sobre sua prática e segundo os próprios docentes o estudo e aplicação do software será de grande ajuda para a aprendizagem dos alunos no tocante ao desenvolvimento de atividades de funções em suas aulas.
Ademais, Oliveira e Pereira (2013) enfatizam que “o software Winplot, por ser um programa que gera simulações e animações, pode contribuir para que os conceitos matemáticos sejam desenvolvidos nos alunos de forma instigante e significativa” (Oliveira; Pereira, 2013, p. 6). Diante do exposto, torna-se evidente a importância da utilização do Winplot como software educativo no ensino de funções.
O software possibilitou um novo olhar para o ensino de função, principalmente sobre o estudo dos gráficos. Assim, vamos agora entender melhor como funciona esse software e como podemos usá-lo em uma aula de Matemática, enfatizando o estudo dos gráficos das funções quadráticas.
O software Winplot no ensino da função quadrática
Primeiramente, iremos compreender o conceito de função quadrática e seu gráfico. Posteriormente, utilizaremos o programa Winplot para analisar o comportamento do gráfico, a partir das variações de cada coeficiente.
Função quadrática
Segundo Dante (2010) chama-se função quadrática toda função cuja lei de formação pode ser indicada por 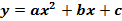 , com
, com 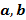 e
e 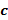 reais e
reais e 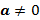
(Obs.: 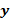 poderá ser escrito por
poderá ser escrito por 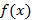 ).
).
Exemplo: 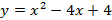 ou
ou 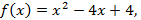 onde
onde 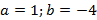 e
e 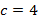
Gráfico da função quadrática
O gráfico de uma função quadrática é sempre uma curva chamada parábola (Dante, 2010).
Veja dois exemplos de gráficos de funções quadráticas. O primeiro com 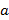 maior que zero
maior que zero 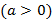 e o segundo com
e o segundo com 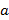 menor que zero
menor que zero 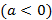 .
.
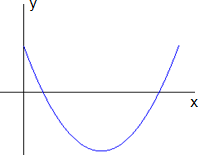
Figura 1: Gráfico da função com 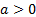
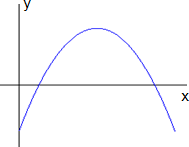
Figura 2: Gráfico da função com 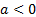
Percebe-se que com 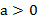 a concavidade do gráfico é voltada para cima e com
a concavidade do gráfico é voltada para cima e com 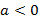 a concavidade é voltada para baixo.
a concavidade é voltada para baixo.
Usando o Winplot na construção de um gráfico
Partindo do pressuposto que o conceito de função já foi abordado, vamos utilizar o software Winplot para construir o gráfico da função 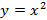
Inicialmente, deve-se abrir o programa clicando duas vezes em sua imagem sobre a qual está representada a Figura 3.

Figura 3: Winplot
Ao abrir o programa, terá esta página inicial:
Figura 4: Janela inicial do programa
Conforme a Figura 4, temos duas opções de abas: Janela e Ajuda. Quando clicamos na aba Janela, podemos encontrar as seguintes opções:
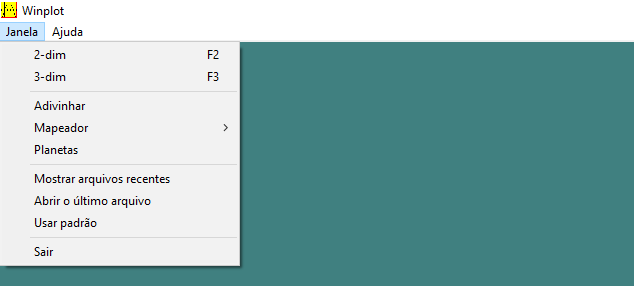
Figura 5: Opções da aba Janela
Ao clicar na opção de gráficos em duas dimensões (2-dim) ou pressionar a tecla F2 do teclado, abrirá:
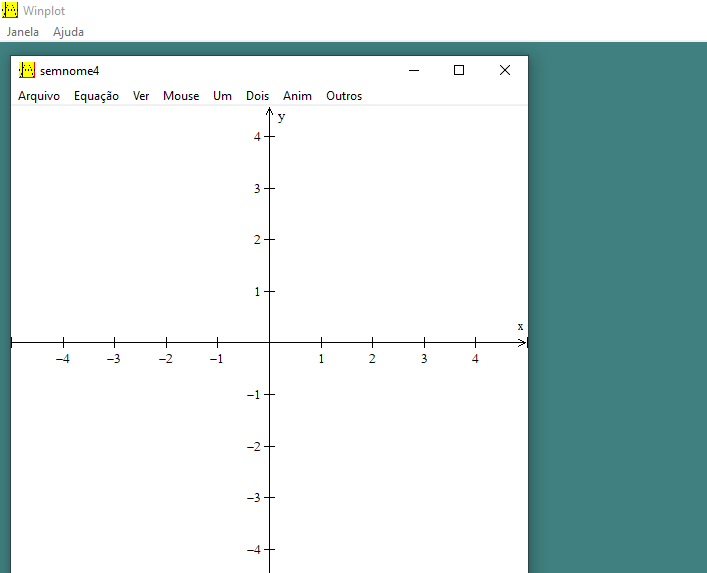
Figura 6: Plano cartesiano em duas dimensões
Clicando em Equação e, em seguida, na opção Explícita, será mostrada a janela onde será inserida a fórmula da função desejada. Veja a seguir.
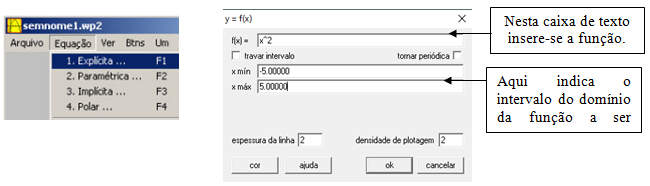
Figura 7: Equação explícita
Após isso, é só pressionar o botão Ok, que o programa desenha o gráfico solicitado:
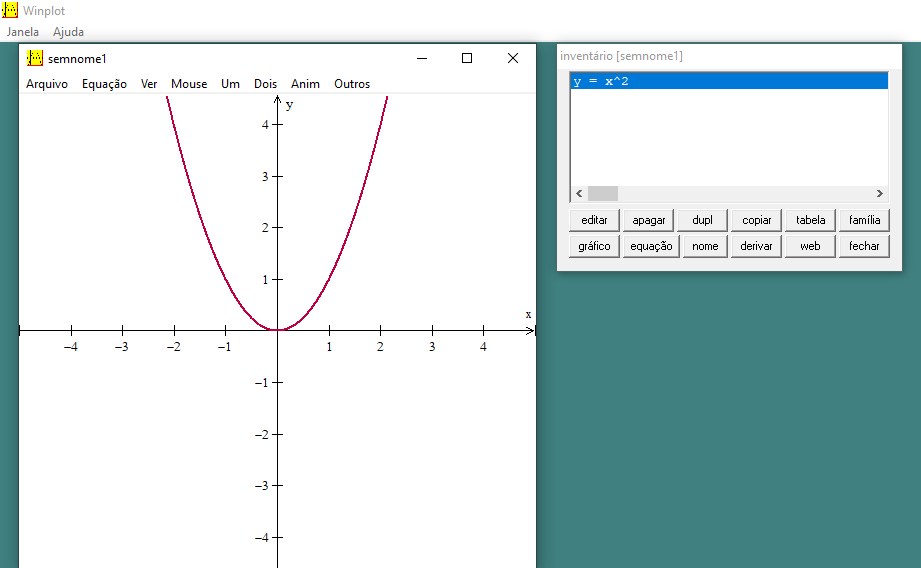
Figura 8: Gráfico gerado pelo Winplot
Como podemos ver, o gráfico é exibido de forma bem simplificada. Alguns detalhes podem ser adicionados ao editá-lo e ao modificar algumas opções de visualização do gráfico. Existem várias opções, porém, no presente trabalho, não será possível detalhar tudo.
Agora que sabemos as etapas que devem ser seguidas para gerar um gráfico, podemos, portanto, fazer os estudos dos coeficientes (analisar as variações de cada um deles) da função quadrática 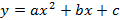 , utilizando o Winplot.
, utilizando o Winplot.
Análise da variação do coeficiente “a”
Dada a função quadrática 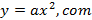
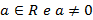 .
.
Procedimentos
· Abrir o programa, e seguir esta sequência: Janela  2dim
2dim  equação
equação 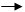 explicita.
explicita.
· Inserir, na caixa de diálogo, a função 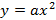 , considerando primeiro
, considerando primeiro 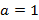 ; posteriormente, clicar em dupl no inventário para plotar outros gráficos, variando o coeficiente
; posteriormente, clicar em dupl no inventário para plotar outros gráficos, variando o coeficiente 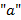 . Cada gráfico é construído em cor diferente dos demais para melhor visualização.
. Cada gráfico é construído em cor diferente dos demais para melhor visualização.
Vamos plotar os gráficos das funções quadráticas, a seguir, em um mesmo plano cartesiano.
» Funções quadráticas com 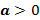
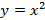 ;
; 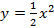 ;
; 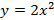 ;
; 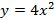
» Funções quadráticas com 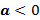
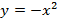 ;
; 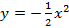 ;
; 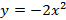 ;
; 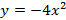
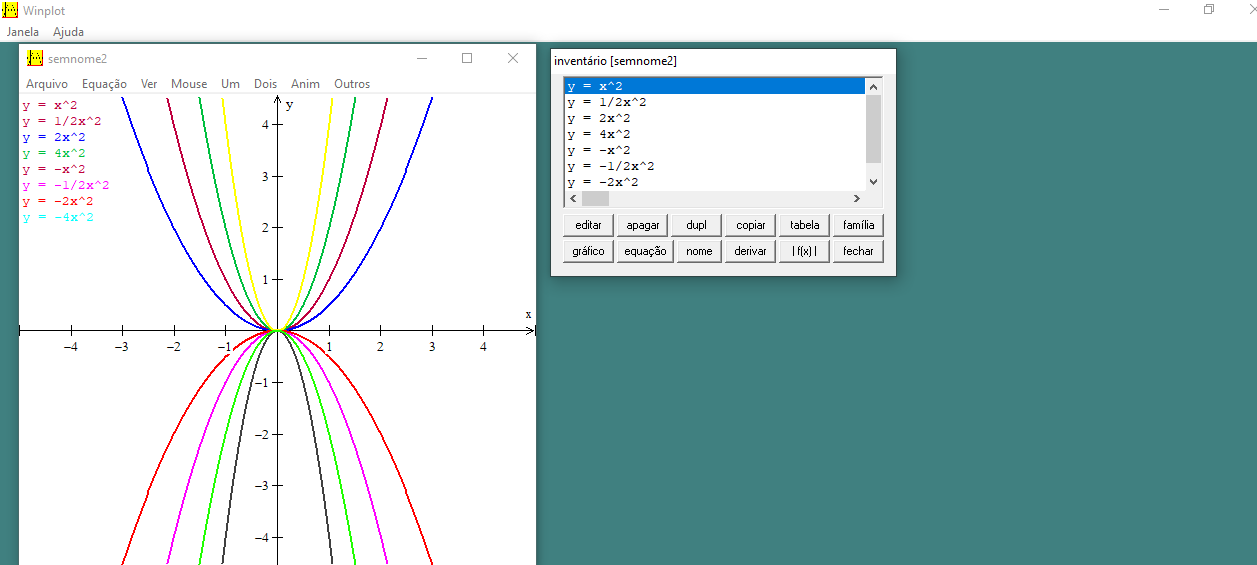
Figura 9: Gráficos da função 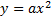
De acordo com a Figura 9, podemos observar os seguintes pontos:
I. Todos possuem um único ponto em comum, a origem do plano;
II. Quando o valor do coeficiente 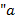 ” aumenta, o gráfico se aproxima mais do eixo das ordenadas (eixo
” aumenta, o gráfico se aproxima mais do eixo das ordenadas (eixo 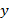 ). Em outras palavras, vai se fechando; quanto menor, mais aberta será a concavidade e mais distante do eixo
). Em outras palavras, vai se fechando; quanto menor, mais aberta será a concavidade e mais distante do eixo 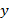 ;
;
III. As funções que possuem o coeficiente 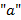 maior que zero (
maior que zero (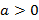 ) têm gráficos (parábolas) com concavidade voltada para cima e que sempre estará acima do eixo das abscissas (eixo
) têm gráficos (parábolas) com concavidade voltada para cima e que sempre estará acima do eixo das abscissas (eixo 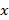 ) para todos os valores não nulos de
) para todos os valores não nulos de 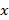 ;
;
IV. As funções que possuem o coeficiente 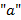 menor que zero (
menor que zero ( 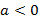 ) têm gráficos (parábolas) com concavidade voltada para baixo e que sempre estará abaixo do eixo das abscissas (eixo
) têm gráficos (parábolas) com concavidade voltada para baixo e que sempre estará abaixo do eixo das abscissas (eixo 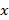 ) para todos os valores não nulos de
) para todos os valores não nulos de 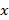 .
.
V. De modo geral, o coeficiente 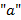 do gráfico da função quadrática é responsável tanto pela abertura quanto pela concavidade da parábola. Além disso, o gráfico da função
do gráfico da função quadrática é responsável tanto pela abertura quanto pela concavidade da parábola. Além disso, o gráfico da função 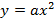 é uma parábola cujo vértice se encontra sempre na origem do plano cartesiano, independentemente do valor do seu coeficiente angular.
é uma parábola cujo vértice se encontra sempre na origem do plano cartesiano, independentemente do valor do seu coeficiente angular.
Análise da variação do coeficiente “b”
Dada a função quadrática 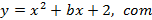
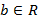 .
.
Procedimentos
· Abrir o programa e seguir essa sequência: Janela  2dim
2dim  equação
equação  explicita.
explicita.
· Inserir na caixa de diálogo a função 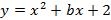 , considerando primeiro
, considerando primeiro 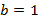 ; posteriormente, clicar em dupl no inventário para plotar outros gráficos, variando o coeficiente
; posteriormente, clicar em dupl no inventário para plotar outros gráficos, variando o coeficiente 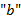 . Cada gráfico construído em cor diferente dos demais, para melhor visualização.
. Cada gráfico construído em cor diferente dos demais, para melhor visualização.
Vamos plotar os gráficos das funções quadráticas, a seguir, em um mesmo plano cartesiano.
» Funções quadráticas com 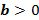 .
.
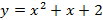 ;
; 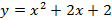 ;
; 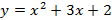
» Funções quadráticas com 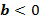 .
.
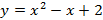 ;
; 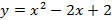 ;
; 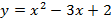
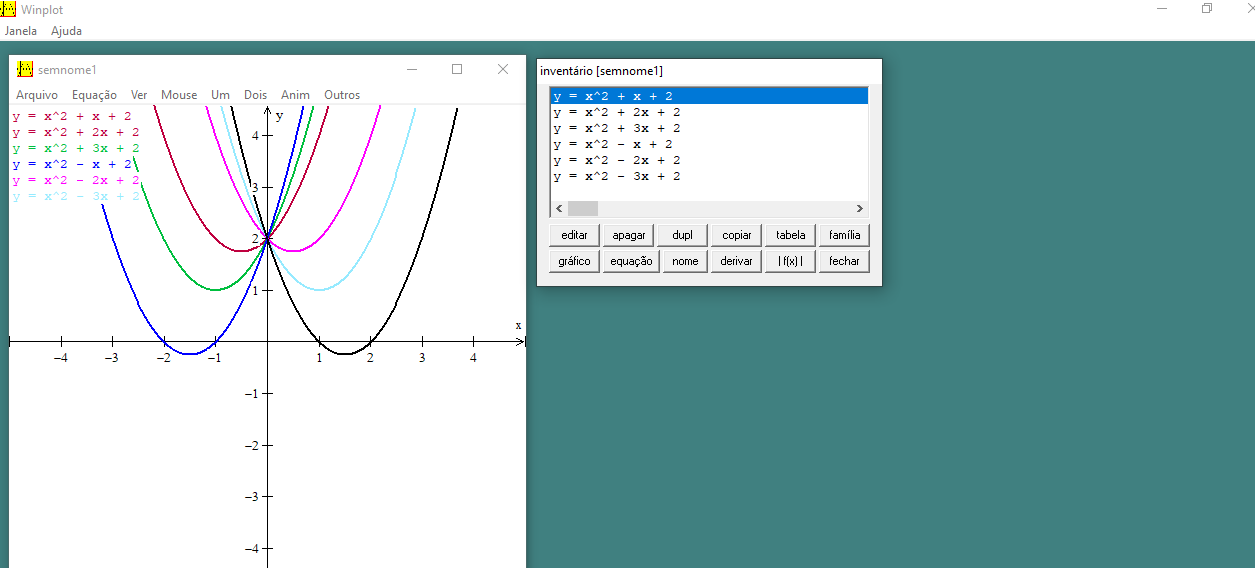
Figura 10: Gráficos da função 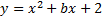
Na figura 10, observamos o comportamento do gráfico em relação ao eixo 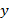 . Podemos perceber que quando o coeficiente
. Podemos perceber que quando o coeficiente 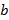 é maior que zero (
é maior que zero ( 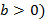 , o gráfico intercepta o eixo
, o gráfico intercepta o eixo 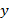 no sentido crescente e quando
no sentido crescente e quando 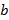 é menor que zero (
é menor que zero ( 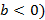 , intercepta no sentido decrescente. Exatamente o que Dante (2010), quando trata dos estudos dos gráficos das funções quadráticas, afirmou sobre o parâmetro
, intercepta no sentido decrescente. Exatamente o que Dante (2010), quando trata dos estudos dos gráficos das funções quadráticas, afirmou sobre o parâmetro 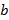 que indica se a parábola intersecta o eixo
que indica se a parábola intersecta o eixo 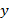 no ramo crescente ou decrescente da parábola, conforme
no ramo crescente ou decrescente da parábola, conforme 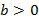 ou
ou 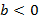 (Dante, 2010).
(Dante, 2010).
Análise da variação do coeficiente “c”
Dada a função quadrática 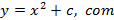
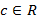 .
.
Procedimentos
· Abrir o programa e seguir essa sequência: Janela 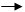 2dim
2dim  equação
equação 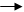 explicita.
explicita.
· Inserir na caixa de diálogo a função 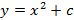 , considerando primeiro
, considerando primeiro 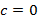 ; posteriormente, clicar em dupl no inventário para plotar outros gráficos, variando o coeficiente
; posteriormente, clicar em dupl no inventário para plotar outros gráficos, variando o coeficiente 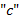 . Cada gráfico construído em cor diferente dos demais, para melhor visualização.
. Cada gráfico construído em cor diferente dos demais, para melhor visualização.
Vamos plotar os gráficos das funções quadráticas a seguir em um mesmo plano cartesiano.
» Funções quadráticas com 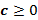 .
.
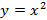 ;
; 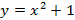 ;
; 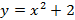
» Funções quadráticas com 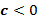 .
.
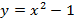 ;
; 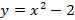 ;
; 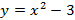
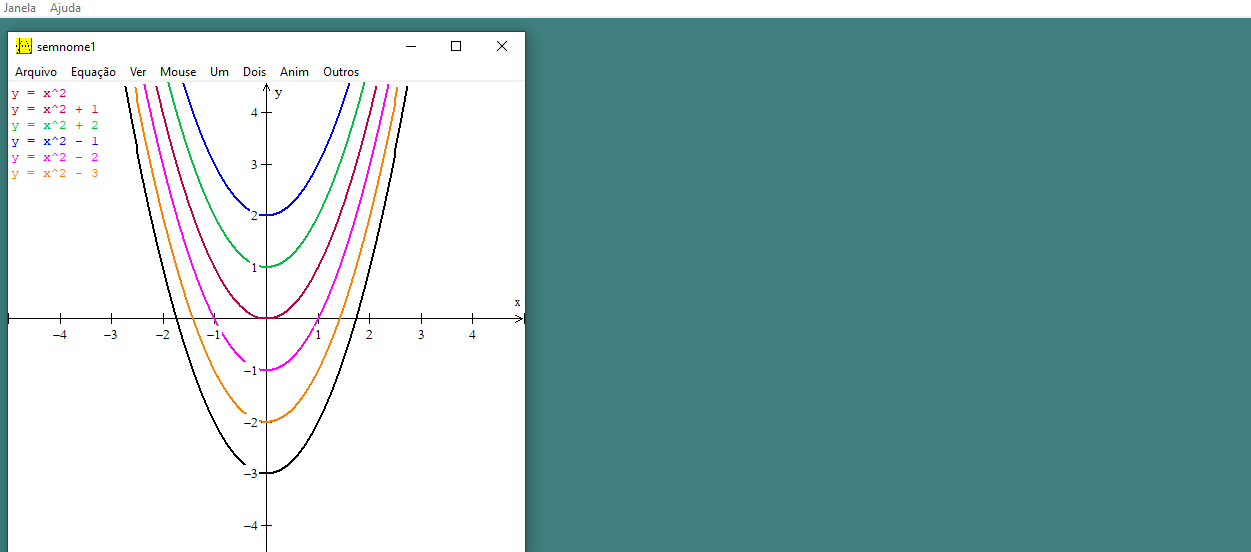
Figura 11: Gráficos da função 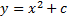
É notório o comportamento do gráfico na Figura 11 quando variamos o coeficiente “ 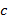 ”. A variação de “
”. A variação de “ 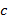 ” é responsável pelo deslocamento vertical da parábola. Quando
” é responsável pelo deslocamento vertical da parábola. Quando 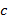 é maior que zero
é maior que zero 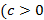 ), o deslocamento do gráfico se faz para cima do eixo
), o deslocamento do gráfico se faz para cima do eixo 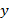 e quando
e quando 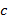 é menor que zero
é menor que zero 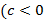 ), o deslocamento se faz para baixo. Podemos também destacar que
), o deslocamento se faz para baixo. Podemos também destacar que 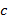 indica o ponto (0,
indica o ponto (0, 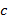 ) onde a parábola intersecta o eixo
) onde a parábola intersecta o eixo 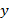 (Dante, 2010).
(Dante, 2010).
Podemos perceber, por esses exemplos, que é possível aprofundar o estudo das funções quadráticas utilizando esse software educativo, pois possui muitas funcionalidades que poderão atrair o interesse dos alunos. As funcionalidades apresentadas são apenas alguns exemplos do que poderá ser abordado em uma aula de Matemática. Logo, com essa proposta, é possível desmistificar a complexidade do estudo de função, por meio da utilização desse programa, proporcionando melhor entendimento e, consequentemente, melhores resultados das aprendizagens dos alunos.
Metodologia
Este trabalho foi desenvolvido por meio de uma pesquisa bibliográfica, de abordagem qualitativa, com artigos científicos e monografias publicadas entre 2010 a 2018, na base do Google Acadêmico e no Portal de Periódicos da Capes. Pizzani et al. (2010) definem a pesquisa bibliográfica como uma pesquisa realizada em livros, periódicos, artigos de jornais, entre outros materiais, cujo objetivo é revisar as principais teorias que norteiam o trabalho científico (Pizzani et al., 2010, p. 2).
Creswell (2010, p. 43) define a abordagem proposta como “um meio para explorar e para entender o significado que os indivíduos ou os grupos atribuem a um problema social ou humano”. A partir da leitura analítica dos textos selecionados, ordenamos e sistematizamos as informações contidas nas fontes de forma a obtermos respostas ao problema da pesquisa.
Foram utilizados como critérios de inclusão artigos que abordassem o tema, pesquisas sobre o uso do Winplot (como software educacional para o ensino da função quadrática e como critério de exclusão) e trabalhos que não tivessem relação direta com a temática estudada.
Considerações finais
A proposta deste trabalho concentrou-se em apresentar as principais contribuições e desafios do software Winplot no ensino da função quadrática, mostrando que a sua utilização acarreta uma aprendizagem significativa, minimizando as grandes dificuldades encontradas no ensino de função.
Os resultados apontam que os desafios mais recorrentes foram, a saber, a falta de conhecimento do software, principalmente por parte dos docentes, as dificuldades no seu manuseio (habilidades) e a desmotivação para a sua utilização, já que a aula tradicional oferece “menos trabalho” para ser elaborada. Sobre as possibilidades, podemos citar os novos conhecimentos adquiridos tanto por parte dos discentes quanto dos docentes, ocasionando uma aprendizagem mútua.
Pelas pesquisas podemos inferir que o software Winplot é uma ferramenta muito relevante para a aprendizagem dos discentes, pois proporciona momentos dinâmicos e diferenciados, que garantem o bom desempenho dos alunos na construção dos conceitos matemáticos, estimulando a curiosidade, ocasionando o interesse pela aprendizagem e desenvolvendo o raciocínio dedutivo.
Conforme exposto, percebe-se que o programa contribui, de forma positiva, como um recurso didático de ensino-aprendizagem. Portanto, torna-se necessário seu uso no ensino da Matemática, sobretudo no ensino de funções quadráticas, oferecendo mais uma ferramenta ao professor para dinamizar suas aulas e oferecendo ao educando uma visão mais simples de compreender os conceitos matemáticos. Além disso, a pesquisa resultou na certeza de que as Tecnologias de Informação e Comunicação (no caso o software Winplot) revelou-se como uma opção para a inserção no planejamento do professor, pois melhora o modelo tradicional de ministração de aula, tornando-a mais dinâmica e auxiliando na construção do conhecimento do aluno.
Acreditamos que esta temática mereça novos olhares, bem como novas pesquisas. Desse modo, as discussões contribuirão para o debate sobre a temática do uso do Winplot como software educativo.
Entendemos que esse trabalho já contribui com outros pesquisadores incentivando ao aprofundamento da discussão em busca de outros aspectos que venham ampliar ainda mais os conhecimentos sobre o uso dos recursos tecnológicos como instrumentos pedagógicos.
Referências
CRESWELL, J. W. W. Projeto de pesquisa: métodos qualitativo, quantitativo e misto. 2ª ed. Porto Alegre: Bookman, 2010.
DANTE, L. R. Matemática: contexto e aplicações. São Paulo: Ática, 2010.
IEZZI, G. et al. Matemática: ciência e aplicações. 2ª ed. São Paulo: Atual, 2004.
JESUS, S. M. C.; SILVA, M. D. F. Estudo das funções afins, quadráticas e equações polinomiais com o auxílio do software Winplot no Ensino Médio. Revista Brasileira de Ensino de Ciência e Tecnologia, Salvador, 2015. Disponível em: https://doi.org/10.3895/rbect.v8n1.1765. Acesso em: 7 dez. 2020.
MODROW, E. S.; SILVA, M. B. A escola e o uso das TIC: limites e possibilidades. Cadernos PDE [on-line]. Curitiba, 2013. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2013/2013_uepg_ped_artigo_elizabeth_santanna_modrow.pdf. Acesso em: 16 dez. 2020.
OLIVEIRA, I. P. S.; PEREIRA, L. C. Uso do software Winplot: uma proposta de ensino-aprendizagem significativa no programa Emitec. Salvador, 2013. Disponível em: http://www.abed.org.br/congresso2013/cd/201.pdf. Acesso em: 28 nov. 2020.
PEREIRA, B. T. O uso das tecnologias da informação e comunicação na prática pedagógica da escola. Curitiba, 2009. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/1381-8.pdf. Acesso em: 18 dez. 2020.
PIZZANI, L. et al. A arte da pesquisa bibliográfica na busca do conhecimento. Rev. Dig. Bibl. Ci. Inf., Campinas, 2010.
SOUSA, I. B.; LINS, I. M.; ABREU, J. D.A utilização dos softwares Winplot e GeoGebra na construção de gráficos de funções no ensino da Matemática. IX EPBBEM – ENCONTRO PARAIBANO DE EDUCAÇÃO MATEMÁTICA. 2016. Disponível em: http://www.editorarealize.com.br/editora/anais/epbem/2016/TRABALHO_EV065_MD1_SA7_ID335_13102016203020.pdf. Acesso em: 04 dez. 2020.
SOUZA, S. E. O uso de recursos didáticos no ensino escolar. I ENCONTRO DE PESQUISA EM EDUCAÇÃO, IV JORNADA DE PRÁTICA DE ENSINO, XIII SEMANA DE PEDAGOGIA DA UEM: “Infância e Práticas Educativas”. Arq. Mudi., 2007. Disponível em: http://www.dma.ufv.br/downloads/MAT%20103/2015-II/slides/Rec%20Didaticos%20-%20MAT%20103%20-%202015-II.pdf. Acesso em: 05 jan. 2021.
TAJRA, S. F. Informática na educação: novas ferramentas pedagógicas para o professor na atualidade. São Paulo: Érica, 2008.
VALENTIM, E. S. O software Winplot e a prática pedagógica do professor de Matemática. Trabalho de conclusão de curso, Universidade Estadual da Paraíba, Campina Grande, 2014. Disponível em: http://dspace.bc.uepb.edu.br/jspui/bitstream/123456789/4460/1/PDF%20-%20%20Erivan%20Sousa%20valentim.pdf. Acesso em: 08 dez. 2020.
Publicado em 14 de junho de 2022
Como citar este artigo (ABNT)
MARINHO, Janailson Silva. O uso do Winplot como software educativo no ensino da função quadrática. Revista Educação Pública, Rio de Janeiro, v. 22, nº 22, 14 de junho de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/22/o-uso-do-winplot-como-software-educativo-no-ensino-da-funcao-quadratica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

