O uso do GeoGebra e de ferramentas digitais na aprendizagem de Geometria Plana e resolução de problemas: uma experiência de sala de aula
Dâmaris Souza Araújo
Aluna do Curso Técnico em Química, Instituto Federal de Educação, Ciência e Tecnologia do Amapá
Kamilly Victoria da Silva
Aluna do Curso Técnico em Química, Instituto Federal de Educação, Ciência e Tecnologia do Amapá
Lays Vitoria de Sousa Miranda
Aluna do Curso Técnico em Química, Instituto Federal de Educação, Ciência e Tecnologia do Amapá
Yara Almeida da Silva Ferreira
Aluna do Curso Técnico em Química, Instituto Federal de Educação, Ciência e Tecnologia do Amapá
Hutson Roger Silva
Licenciado em Matemática (UFU)
“A Matemática é vista atualmente como uma disciplina que traz grandes dificuldades no processo ensino-aprendizagem, tanto para os alunos como aos professores envolvidos no mesmo” (Piovesan; Zanardini, 2008, p. 2). Isso acontece porque muitas vezes os alunos não são motivados e não conseguem assimilar os assuntos abordados pelo professor.
A finalidade da Educação Matemática é fazer o estudante compreender e se apropriar da própria Matemática, “concebida como um conjunto de resultados, métodos, procedimentos, algoritmos etc.” (Miguel; Miorim, 2004, p. 70 apud Piovesan; Zanardini, 2008, p. 3). Mas sabe-se que muitos estudantes têm dificuldades no processo de aprendizagem da Matemática e não conseguem ter suas dúvidas sanadas ou não têm interesse algum, tornando necessário então o professor tentar se apropriar de diferentes metodologias ou até mesmo ferramentas para levar à sala de aula para deixar sua aula melhor e mais dinâmica e fazer com que os alunos se interessem pela busca de conhecimento, pois só assim serão capazes de desenvolver habilidades matemáticas em diferentes níveis e, consequentemente, criar, resolver, ler e interpretar problemas. Uma alternativa que pode auxiliar e ser importante nesse processo é o uso de plataformas que contenham e disponibilizem recursos que ajudem os alunos na resolução de exercícios ou de problemas. Um grande aliado nisso pode ser o GeoGebra, que, além de poder ser usado tanto pelos professores quanto pelos alunos, dispõe dos mais diversos assuntos de Matemática, como: Trigonometria, cálculos algébricos, Estatística e Geometria Plana.
Tendo isso em vista, pensou-se no desenvolvimento deste projeto como forma de avaliar e instigar os alunos a resolver questões presentes no próprio cotidiano atreladas à aprendizagem do conteúdo da sala de aula usando o GeoGebra, consoante a resolução de problemas, “que consiste na contextualização de situações aplicáveis no cotidiano que exigem uma solução que requer estratégia para ser enfrentada” (Rodrigues; Magalhães, 2012, p. 2). Portanto, este trabalho mostra como o GeoGebra e outras ferramentas foram aplicadas no ensino de Geometria Plana.
O presente trabalho consistiu em calcular a área e o perímetro de municípios do Estado do Amapá, tendo como participantes alunas da turma do 2º ano do Curso Técnico em Química (em 2021) do Instituto Federal do Amapá (IFAP); a turma foi dividida em grupos contendo quatro integrantes e cada um foi responsável por dois municípios. Este trabalho foi desenvolvido em torno dos municípios de Laranjal do Jari e de Vitória do Jari. Além disso, teve como objetivo proporcionar uma experiência diferente aos alunos, que tiveram total autonomia sobre as ferramentas virtuais a usar para a sua realização, além dos conceitos de Geometria Plana para planificar, calcular a área e perímetro dos municípios, comparar os valores obtidos com os valores reais e, por fim, consumar como foi a experiência e o que ela acrescentou na aprendizagem dos discentes. Os resultados estão dispostos em tabelas, amparados por discussões acerca deles.
Amapá
Segundo dados do IBGE (2020), o Estado do Amapá possui área de 142.470,762km², com população estimada em 861.773 pessoas, distribuídas em seus dezesseis municípios. De acordo com Guitarrara (2009), o estado faz fronteira com o Pará, a oeste e sul e Guiana Francesa e Suriname a noroeste. O Amapá é um estado da Região Norte do Brasil. O atual estado fazia parte do Pará; quando desmembrado, em 1943, tornou-se o Território Federal do Amapá, só passando a ser declarado estado no ano de 1988. Grande parte de seu território é composto por florestas e possui muitos rios, que fazem parte da bacia amazônica; a maioria deságua no Rio Amazonas.
Laranjal do Jari
Segundo dados do Governo do Estado do Amapá (20--), o município de Laranjal do Jari está localizado na região sul do estado; com área de 31.170,3km², o município faz fronteira com municípios como Oiapoque, Pedra Branca do Amapari, Mazagão e a Guiana Francesa; possui população estimada em 45.712 habitantes. Seu perímetro aproximado é de 1.287,28km e a escala de seu mapa a ser utilizado no presente trabalho é 1:25. O município de Laranjal do Jari foi criado em 6 de dezembro de 1987.
De acordo com o Instituto de Pesquisas Científicas e Tecnológicas do Estado do Amapá – IEPA (2004), o município possui histórico de extrativismo, já tendo episódios com a exploração das drogas do sertão, borracha e castanha do Brasil; ficou conhecido pela fábrica de celulose que no passado era a base econômica da região e existe até hoje, porém está cada vez mais fraca e contando com cada vez menos trabalhadores. Grande parte da extensão de seu território se deve ao Parque Nacional das Montanhas Tumucumaque, que abriga diversas comunidades indígenas; é o maior parque nacional do Brasil e o maior em florestas tropicais do mundo.
Vitória do Jari
Segundo dados do Portal do Governo do Amapá (20--), o município de Vitória do Jari está localizado na parte sul do Amapá e possui área equivalente a 2.428,0km², com população estimada em 14.364 habitantes. O município faz limite com os municípios de Mazagão, ao norte, Laranjal do Jari, a noroeste, e Gurupá/PA ao sul. O seu perímetro aproximado é de 305,41km e a escala do mapa a ser utilizada neste trabalho é de 1:6,25. O município de Vitória do Jari, localizado na parte sul do Amapá, foi criado pela Lei nº 171, de 08 de setembro de 1994.
De acordo com a Prefeitura Municipal de Vitória do Jari (20--), suas origens estão diretamente ligadas à história de desenvolvimento de Laranjal do Jari, sobretudo aos acontecimentos referentes à instalação e funcionamento do Projeto Jari Florestal. As principais atividades produtivas são cooperativas voltadas ao extrativismo; o trabalho da população local movimenta a pequena economia do município pela agricultura, com escoamento de produção, além do comércio e serviços locais. Ainda de acordo com o Portal do Governo do Amapá (20--), a economia do município também gira em torno da fábrica de celulose de uma empresa sediada no Pará que mantém em seu quadro centenas de empregados de Vitória do Jari.
Material e metodologia
Por possuir caráter formativo, o modelo de pesquisa realizado foi de origem qualitativa, devido ao fato de terem sido utilizados métodos de estudo das relações sociais, pois se trata de uma análise qualitativa, quando entram em jogo anotações para descrever e compreender uma situação, mais do que números para enumerar as frequências de comportamentos.
Desse modo, este tipo de pesquisa é feito para melhor compreender os fenômenos que ocorrem, possibilitando também uma reflexão social que pode vir a ser aplicada, neste caso, no âmbito acadêmico, porque os métodos qualitativos têm papel importante no campo dos estudos organizacionais.
Conforme o Instituto GeoGebra São Paulo (20--), o GeoGebra é um software de Matemática dinâmica gratuito e multiplataforma para todos os níveis de ensino; ele combina Geometria, Álgebra, tabelas, gráficos, Estatística e Cálculo numa única aplicação. Assim, utilizou-se o aplicativo e realizou-se um esboço do mapa real dos municípios de Laranjal do Jari e Vitória do Jari, seguindo sua escala real e tamanho, visto que não utilizamos todos os instrumentos e recursos disponíveis no software, embora ele seja bastante interessante. Pode-se observar o esboço, respectivamente, nas Figuras 1 e 2.
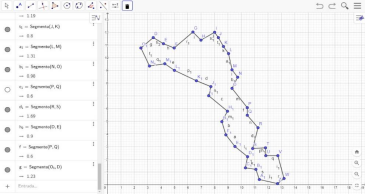
Figura 1: Mapa esboçado no GeoGebra – Laranjal do Jari
Fonte: Baseado no GeoGebra (2021).
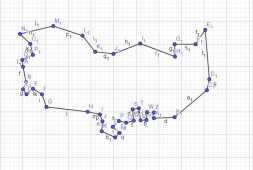
Figura 2: Mapa esboçado no GeoGebra – Vitória do Jari
Fonte: Baseado no GeoGebra (2021).
Apesar de a tentativa de realizar o objetivo a partir do software não ter sido bem-sucedida, utilizou-se o programa Google Earth para encontrar o perímetro de Laranjal do Jari e Vitória do Jari e então foram realizados os cálculos necessários. Os mapas obtidos no Google Earth podem ser observados, respectivamente, nas Figuras 3 e 4.
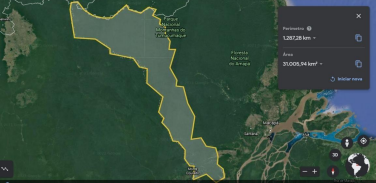
Figura 3: Mapa obtido por meio do Google Earth – Laranjal do Jari
Fonte: Baseado no Google Earth (2021).
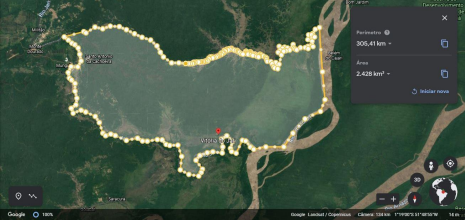
Figura 4: Mapa obtido por meio do Google Earth – Vitória do Jari
Fonte: Baseado no Google Earth (2021).
Desse modo, no papel A4 desenhou-se um mapa seguindo o formato do plano cartesiano do GeoGebra, mas utilizando retas ao invés da planificação real do mapa, tentando deixá-lo o mais semelhante possível, em termos de tamanho, a fim de obter um resultado muito parecido para a execução dos cálculos (de área e perímetro) com o valor real. O mapa de Laranjal do Jari e Vitória do Jari feito à mão pode ser observado, respectivamente, nas Figuras 5 e 6.
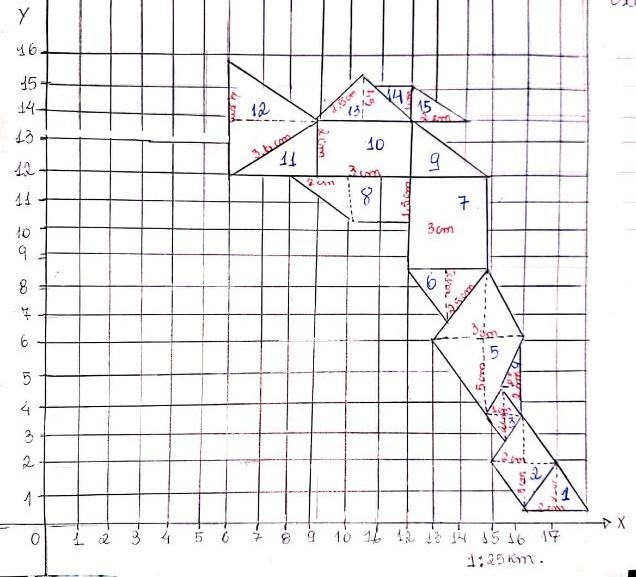
Figura 5: Mapa feito à mão e com escala criada pelo autor – Laranjal do Jari
Legenda do mapa:
Números com cor azul servem para localizar a determinada figura geométrica;
Números em vermelho indicam as medidas dos lados das figuras.
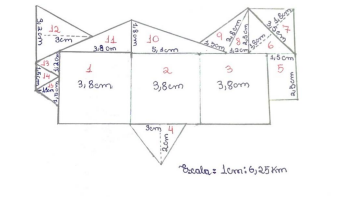
Figura 6: Mapa feito à mão e com escala criada pelo autor – Vitória do Jari
Legenda do mapa:
Números em vermelho servem para localizar determinada figura geométrica;
Números com cor preta indicam as medidas dos lados das figuras.
Percebe-se então que o mapa foi dividido em figuras geométricas ou planas que estão com suas respectivas medidas com a escala especificada. Logo, isso implicou a deformação e a divergência dos valores obtidos após a comparação.
Resultados e discussões
A fim de realizar os cálculos necessários, usaram-se os valores do mapa geométrico feito de acordo com o valor da escala criada: Laranjal do Jari: 1cm no mapa representa 25km; Vitória do Jari: 1cm no mapa representa 6,25km. Então, para calcular a área de determinada figura, dependendo de qual seja ela, utilizou-se a fórmula matemática de cálculo de área. Por exemplo: para calcular a área de um triângulo que possui base (b) x e altura (h) y, basta multiplicar os valores (de x e de y) por 25 ou 6,25, que é o valor equivalente a 1cm (usado para representar o tamanho do mapa). Exemplo: utilizando a escala de Laranjal do Jari, um triângulo do mapa possui base = 1 e altura= 1; logo, o valor utilizado para calcular sua área seria: 1x25km = 25km (valor da base) e 1x25km = 25km (valor da altura). Portanto, a área desse triângulo seria obtida da seguinte maneira: A = b x h/2; então A = 25x25/2 = 625/2 = 312,5 km2.
Tabela 1: Cálculos da área de figura – Laranjal do Jari
Figura específica e figura geométrica |
Área calculada |
Figura 1 – Triângulo |
A = b.h/2 = 50.50/2 = 1.250km2 |
Figura 2 – Losango |
A = d.D/2 = 75.50/2 = 1.875km2 |
Figura 3 – Losango |
A = d.D/2 = 50.25/2 = 525km2 |
Figura 4 – Triângulo |
A = b.h/2 = 50.12,5/2 = 312,5km2 |
Figura 5 – Losango |
A = d.D/2 = 125.74/2 = 4.687,5km2 |
Figura 6 – Triângulo |
A = b.h/2 = 75.50/2 = 1.875km2 |
Figura 7 – Quadrado |
A = L2=75.75=5.625km2 |
Figura 8 – Triângulo + retângulo |
Triângulo: A = b.h/2 = 50.37,5/2= Retângulo: A = b.h = 50.37,5 = 937,5 + 1.875 = 2.812,5 km2 é a área da figura 8 |
Figura 9 – Triângulo |
A = b.h/2 =75.50/2 = 1.875km2 |
Figura 10 – Retângulo |
A = b.h = 75.50 = 3.750km2 |
Figura 11 – Triângulo |
A = b.h/2 = 75.50/2 = 1.875km2 |
Figura 12 – Triângulo |
A = b.h/2 = 100.75/2 = 3.750km2 |
Figura 13 – Triângulo |
A = b.h/2 = 75.37,5/2 = 1.406,25km2 |
Figura 14 – Triângulo |
A = b.h/2 = 25.25/2 = 312,5km2 |
Figura 15 – Triângulo |
A = b.h/2 = 50.25/2 = 625km2 |
Tendo em vista que a área total do mapa é a soma das áreas de todas as figuras, temos: 1.250km2+ 1.875km2+525km2+312,5km2+4.687,5km2+ 1.875km2+5.625km2+2.812,5km2+1.875km2+ 3.750km2+1.874km2+3.750km2+1.406,25km2+312,5km2+625km2= 32.656,25km2
Tabela 2: Figura e seu respectivo perímetro – Laranjal do Jari

Perímetro aproximado encontrado utilizando a plataforma Google Earth = 1.287,28km; perímetro total aproximado encontrado a partir do mapa geométrico = 1.165km.
Tabela 3: Cálculos da área de figura – Vitória do Jari
Figura específica e figura geométrica |
Área calculada |
Figura 1 – Quadrado |
A = L2 = 23,752 = 564,06km² |
Figura 2 – Quadrado |
A = L2 = 23,752 = 564,06km² |
Figura 3 – Quadrado |
A = L2 = 23,752 = 564,06km² |
Figura 4 – Triângulo |
A = b.h/2 = 12,5.18,75/2 =117,18km² |
Figura 5 – Retângulo |
A = b.h = 15,62.9,37= 146,35km² |
Figura 6 – Triângulo |
A = b.h/2 = 21,87.11,25/2 = 123,01km² |
Figura 7 – Triângulo |
A = b.h/2 = 21,87.11,25 / 2 = 123,01km² |
Figura 8 – Triângulo retângulo |
A = b.h/2 =15,62.7,5/2 = 58,57km² |
Figura 9 – Triângulo retângulo |
A = b.h/2 =17,5. 9,37/2 = 81,98km² |
Figura 10 – Triângulo retângulo |
A = b.h/2 = 31,87.11,25/2 = 179,26km² |
Figura 11 – Triângulo retângulo |
A = b.h/2 = 23,75.11,25/2 = 133,59km² |
Figura 12 – Triângulo |
A = b.h/2 = 20.18,75/2 = 187,5km² |
Figura 13 – Triângulo |
A = b.h/2 = 6,87.7,5/2 = 25,76km² |
Figura 14 – Triângulo |
A = b.h/2 = 6,87.9,37/2 = 32,18km² |
Figura 15 – Triângulo |
A = b.h/2 = 6,87.9,37/2 = 32,18km² |
Tendo em vista que a área total do mapa é a soma das áreas de todas as figuras, temos: A (total) = 564,06km² + 564,06km² + 564,06km² + 117,18km² + 146,35km²+ 123,01km² + 123,01km² + 58,57km² + 81,98km² + 179,26km² + 133,59km² + 187,5km² + 25,76km² + 32,18km² + 32,18km² = 2.932,75km².
Para calcular o perímetro, foi necessário medir a lateral de todo o mapa feito a lápis e obteve-se como resultado 44,2cm. Numa regra de três simples, temos que: 1,6cm equivalem a 10km (escala utilizada durante o processo). Logo, achou-se quanto equivalem 44,2cm em km.

Figura 7: Regra de três simples para calcular o perímetro – Vitória do Jari
O perímetro aproximado encontrado utilizando a plataforma Google Earth = 305,41km; o perímetro total aproximado encontrado a partir do mapa geométrico = 276,25km.
Tabela 4: Comparação e margem de erro do perímetro – Laranjal do Jari
Perímetro (km) |
Perímetro no mapa manual |
Margem de erro (subtração) |
1.287.38km |
1.165km |
1.287,28 – 1.165 = 122,28km |
Tabela 5: Comparação e margem de erro da área – Laranjal do Jari
Área (km²) |
Área no mapa manual |
Margem de erro (subtração) |
31.170,3km² |
32.656,25km² |
32.656,25 – 31.170,3 = 1.485,95km² |
Tabela 6: Comparação e margem de erro do perímetro – Vitória do Jari
Perímetro (km) |
Perímetro do mapa manual |
Margem de erro (subtração) |
305,41km |
276,25km |
305,41km – 276,25km = 29,16km |
Tabela 7: Comparação e margem de erro da área – Vitória do Jari
Área (km²) |
Área no mapa manual |
Margem de erro (subtração) |
2.428km² |
2.932,75km² |
2.932,75km² – 2.428km² = 504,75km² |
De acordo com os resultados obtidos, pôde-se observar que a margem de erro de Laranjal do Jari, nas Tabelas 4 e 5, pode ser considerada pequena, com valor para a área igual a 1.485,95km² e para o perímetro igual a 122,28km. Nas Tabelas 6 e 7, temos a comparação do perímetro e área de Vitória do Jari obtidos a partir de cálculos utilizando o mapa geométrico com o perímetro e área reais fornecidos pela plataforma digital Google Earth, com margem de erro para a área igual a 504,74km² e para o perímetro igual a 29,16km. Pode-se notar que o desvio obtido foi pequeno.
Considerações finais
Levando em consideração os fatos analisados, concluiu-se que os objetivos iniciais foram alcançados com êxito, apesar das dificuldades encontradas ao tentar usar a plataforma virtual GeoGebra. Foi possível obter um resultado extremamente próximo dos reais, principalmente comparando os perímetros, que apresentaram parâmetros muito semelhantes aos encontrados inicialmente. As margens de erro foram baixíssimas tendo em vista a grande extensão territorial dos municípios.
A pesquisa consumada acarretou diversos benefícios e trouxe novos aprendizados úteis considerando o contexto em que se vive. Foram aplicados conceitos geométricos no cotidiano, buscaram-se dados (como área e perímetro) em ferramentas online, haja vista que foi difícil encontrar tais informações em sites ou revistas. Além disso, de alguma forma “comprovaram-se" os dados que estão disponíveis na internet ou ao menos se chegou a um resultado aproximado, além de que foi possível observar que não é algo distante de nós. A pesquisa possibilitou a procura e o melhor conhecimento sobre os municípios do Estado do Amapá.
Diante da experiência pela qual passamos, de resolver problemas, após responder um questionário contendo cinco perguntas aplicado pelo orientador a fim de coletar dados, foi possível concluir que o GeoGebra não havia sido utilizado por nenhuma das alunas que realizaram este trabalho, o que não impediu que fosse realizado; fazer a pesquisa e usar os programas para a sua realização foi uma experiência boa; apenas duas alunas já tinham trabalhado com Matemática aplicada ao cotidiano e o grupo acredita que foi possível aplicar com êxito os conceitos de Geometria estudados em sala de aula voltados para o cotidiano.
Referências
AMAPÁ. Laranjal do Jari. Portal Governo do Amapá, 20--. Disponível em: https://www.portal.ap.gov.br/conheca/laranjal-do-jari. Acesso em: 23 abr. 2021.
AMAPÁ. Vitória do Jari. Portal Governo do Amapá, 20--. Disponível em: https://www.portal.ap.gov.br/conheca/vitoria-do-jari. Acesso em: 27 abr. 2021.
GUITARRARA, Paloma. Amapá. Mundo Educação. 2009. Disponível em: https://mundoeducacao.uol.com.br/geografia/amapa.htm. Acesso em: 29 abr. 2021.
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA (IBGE). Amapá, cidades e estados. Rio de Janeiro: IBGE, 2020. Disponível em: https://www.ibge.gov.br/cidades-e-estados/ap.html. Acesso em: 29 abr. 2021.
INSTITUTO DE PESQUISAS CIENTÍFICAS E TECNOLÓGICAS DO ESTADO DO AMAPÁ (IEPA). Laranjal do Jari: realidades que devem ser conhecidas. Coord. Benedito Vitor Rabelo et al. Macapá: IEPA, 2004.
INTERNATIONAL GEOGEBRA INSTITUTE (IGI). Sobre o GeoGebra. Instituto Geogebra de São Paulo, 20--. Disponível em: https://www.pucsp.br/geogebrasp/geogebra.html. Acesso em: 29 abr. 2021.
PREFEITURA MUNICIPAL DE VITÓRIA DO JARI. História. 20--. Disponível em: https://www.vitoriadojari.ap.gov.br/pagina/historia. Acesso em: 27 abr. 2021.
PIOVESAN, Sucileiva; B. ZANARDINI, João. O ensino e aprendizagem da Matemática por meio da metodologia de resolução de problemas: algumas considerações. Cascavel: Universidade Estadual do Oeste do Paraná. Programa de Desenvolvimento Educacional – PDE, 2008, Disponível em: http://www.gestaoescolar.diaadia.pr.gov.br/arquivos/File/producoes_pde/artigo_sucileiva_baldissera_piovesan.pdf. Acesso em: 05 out. 2021.
RODRIGUES, Adriano; MAGALHÃES, Shirlei. A resolução de problemas nas aulas de Matemática: diagnosticando a prática pedagógica. Varginha: Centro Universitário do Sul de Minas, 2012. Disponível em: http://www.educadores.diaadia.pr.gov.br/arquivos/File/setembro2012/matematica_artigos/artigo_rodrigues_magalhaes.pdf. Acesso em: 05 out. 2021.
Anexo
Perguntas em grupo
1. Alguém do grupo já trabalhou com o GeoGebra antes?
2. Como o grupo avalia a atividade (boa, ruim, ótima)?
3. Já trabalharam Matemática aplicada no cotidiano alguma vez?
4. Quais foram as dificuldades do grupo?
5. O que o grupo acredita que pode aprender com esse trabalho?
Publicado em 09 de agosto de 2022
Como citar este artigo (ABNT)
ARAÚJO, Dâmaris Souza; SILVA, Kamilly Victoria da; MIRANDA, Lays Vitoria de Sousa; FERREIRA, Yara Almeida da Silva; SILVA, Hutson Roger. O uso do GeoGebra e de ferramentas digitais na aprendizagem de Geometria Plana e resolução de problemas: uma experiência de sala de aula. Revista Educação Pública, Rio de Janeiro, v. 22, nº 29, 9 de agosto de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/29/o-uso-do-geogebra-e-de-ferramentas-digitais-na-aprendizagem-de-geometria-plana-e-resolucao-de-problemas-uma-experiencia-de-sala-de-aula
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

