Utilizando jogos para ensinar Matemática
Flávia Lima Ciríaco
Doutora em Ciência da Educação
O ensino da Matemática é bastante complexo, já que sua aprendizagem depende de uma grande variedade de fatores. Segundo Groenwald e Timm (2007), para aprender matemática é preciso que se desenvolva o raciocínio lógico e sejam estimulados o pensamento independente, a criatividade e a capacidade de resolver problemas. Dessa maneira, os educadores matemáticos devem concentrar-se em aumentar a motivação para a aprendizagem, desenvolver a autoconfiança, organização, concentração, atenção, raciocínio lógico-dedutivo e senso cooperativo, aumentando a socialização e as interações interpessoais.
Considerando tais aspectos e percebendo que a maioria dos alunos não apresenta grande interesse em Matemática, achando sempre tudo complicado e difícil, e que, por outro lado, eles rapidamente entendem as regras e participam com entusiasmo de atividades lúdicas, torna-se clara a valia da utilização de jogos para complementar o estudo dessa disciplina, já que o jogo estimula e socializa, é fonte de diversão e aprendizado e ajuda a desenvolver nos alunos capacidades, conhecimentos, atitudes, habilidades cognitivas e sociais.
Nesse sentido, Groenwald e Timm (2007) estimulam o uso de jogos e curiosidades no ensino da Matemática, com o objetivo de mudar a rotina da classe, despertar o interesse do aluno e fazê-lo gostar de aprender essa disciplina, devido a seu caráter lúdico, desenvolvedor de técnicas intelectuais e formador de relações sociais.
Além disso, Batllori (2006) cita que, através dos jogos, é possível proporcionar experiências, estimular a aceitação de normas e hierarquias, o trabalho em equipe e o respeito pelos outros, já que, quando o estudante joga na escola e brinca com outros de idade aproximada a sua, frequentemente de várias procedências e culturas, adquire importantes meios para sua socialização.
Sendo assim, entende-se que o entusiasmo demonstrado pelos alunos, durante os jogos, deve ser aproveitado para a aquisição de novos conhecimentos matemáticos, para consolidação dos que já possuem tal conhecimentos e para auxiliar o desenvolvimento completo do estudante.
Fundamentação teórica
É longa a discussão sobre os problemas encontrados em sala de aula a respeito de por que o aluno deixa a escola sem saber e sem entender parte da Matemática.
Com o intuito de minimizar esse problema, pensou-se na utilização de jogos, envolvendo conteúdos matemáticos, a serem utilizados em sala de aula.
A história mostra que tal prática não é novidade, de acordo com Kishimoto (apud Ferrarezi, 2005), Platão se utilizou de jogos objetivando apresentar a Matemática de forma concreta, para depois em um segundo nível usar abstrações. Também era uma prática romana se utilizar de jogos a fim de transmitir valores e costumes. Têm-se relatos de que os jesuítas, em suas aulas, praticavam jogos de emulação (rivalidade, competição) visando o aperfeiçoamento da capacidade oratória dos alunos.
Portanto, não é novidade a utilização de jogos para facilitar a aprendizagem, independente da disciplina a ser estudada.
Borin (1996) apresenta como justificativa à introdução de jogos nas aulas de Matemática a possibilidade de diminuir bloqueios apresentados por muitos alunos que temem a Matemática e sentem-se incapacitados para aprendê-la. A situação de jogo leva o aluno a uma grande motivação, se envolvendo nas atividades, ao mesmo tempo em que esses trabalham com Matemática, sem constrangimentos, apresentando melhor desempenho e atitudes positivas frente a seus processos de aprendizagem.
Batllori (2006) discorre sobre algumas capacidades que podem ser desenvolvidas com o jogo, tais como astúcia, talento, confiança, comunicação, imaginação, aquisição de novos conhecimentos e experiências e observação de novos procedimentos. Também cita os jogos como fator importante na busca de alternativas para a resolução de problemas ou dificuldades e no estímulo à aceitação de normas, hierarquias e trabalho em equipe, considerando também que podem ajudar o desenvolvimento físico e mental, pois ampliam as habilidades manuais e mobilidade, além da lógica e do senso comum.
Diversos autores, como Borin e Batllori, fazem referência a uma mudança em todo o desenvolvimento das aulas quando da utilização de jogos. Borin (1996) enfatiza que, nesse processo, o aluno passa a ser um elemento ativo na aprendizagem, vivenciando a construção do seu saber e deixando de ser um ouvinte passivo. Batllori (2006) destaca que essa manifestação espontânea da criança, sem censura e convenções, de forma séria e interessada, mostra como ela realmente é, sendo uma forma insuperável de aprendizagem para os educadores, ajudando também na elaboração de novas estratégias.
Outro importante aspecto destacado por Batllori (2006) é a vertente socializante dos jogos, pois com eles as crianças aprendem a conviver e respeitar outras pessoas e culturas, em especial quando jogam juntas para alcançar um objetivo comum, trabalhando em equipe e distribuindo tarefas. A relevância desse aspecto é citada no Currículo Básico para a Escola Pública do Estado do Paraná:
Sendo uma espécie social o ser humano se caracteriza pela construção de sua individualidade através da relação com o outro. O sujeito se constitui, assim, em virtude de processos múltiplos de interação com o meio sociocultural, pela presença de outros indivíduos e/ou objetivo culturalmente inseridos e definidos (Lima, 2003, p. 18).
Por fim, encontramos destacado nos Parâmetros Curriculares Nacionais (Brasil, 1998) que um aspecto relevante nos jogos é o desafio que eles provocam nos alunos, gerando interesse e prazer; dando ênfase à importância de que os jogos façam parte da cultura escolar, cabendo ao professor analisar e avaliar a potencialidade educativa dos diferentes jogos e o aspecto curricular que deseja desenvolver.
A aula de Matemática e o jogo
A utilização de jogos nas aulas de matemática é uma maneira descontraída de apresentação do conteúdo, abrindo uma nova perspectiva para que o aluno aprenda e instituindo um vínculo mais forte na relação professor/aluno, dando margem ao professor na descoberta das dúvidas com relação aos conteúdos que representam alguma dificuldade do aluno.
Existe uma variedade de jogos matemáticos: os já comprados prontos, os que necessitam ser confeccionados e os virtuais. Todos esses podem ser utilizados pelo professor e seus alunos, modificando o cotidiano das aulas de matemática, atraindo o aluno pela apresentação dinâmica e diferenciada. Dessa maneira, cabe ao professor investigar e analisar quais os jogos que melhor se adaptam aos conteúdos pretendidos.
Surge assim, a constatação da necessidade de um estudo aprofundado acerca da forma mais adequada para a apresentação e desenvolvimento desses recursos dentro da disciplina e a melhor maneira para atingir os objetivos desejados.
Não basta conhecer os jogos e saber jogar. É necessário que o professor consiga aliar de forma interativa e dinâmica esse recurso, para não persistir na rotina, tão conhecida, da sala de aula.
Uma das vantagens ao se trabalhar com jogos é a facilidade de interação com as outras disciplinas da série trabalhada.
Os jogos despertam a atenção de praticamente todos os alunos. Ao que parece, quando estão jogando, se divertem sem o compromisso de aprender algo imposto pelos conteúdos apresentados comumente pelos professores.
Essa despreocupação e o interesse dos alunos podem ser amplamente aproveitados em favor do professor, trabalhando assim, os conteúdos necessários, de maneira mais agradável e de forma que o aluno se aproprie deles sem perceber e sem se martirizar porque não entende Matemática.
Esse pensamento é partilhado por diversos autores, como Borin (1996) e Malba Tahan (1965).
Perspectiva interdisciplinar do uso de jogos em Matemática
Uma das vantagens ao se trabalhar com jogos é a facilidade de interação com as outras disciplinas da série trabalhada.
Podemos trabalhar os jogos de Matemática com a participação de outras disciplinas como:
- Artes – confecção dos jogos: utilização de diferentes técnicas e materiais.
- Ciências – uso de material reciclado para a confecção dos jogos, oportunizando o estudo a respeito da reciclagem.
- Educação Física – formação de grupos, convivência, aceitação e cumprimento de regras.
- Geografia – complementação do estudo realizado em História, trabalhando a localização dos países onde os jogos surgiram, os hábitos desses povos na época da criação dos jogos e atualmente.
- História – onde e como surgiram alguns jogos.
- Língua Estrangeira – expressões e nomes usados em alguns jogos que não são palavras da língua portuguesa.
- Português – A importância da leitura e interpretação das regras dos jogos.
Objetivos
O objetivo do trabalho é repensar a possibilidade em aliar o uso dos jogos ao cotidiano do professor, auxiliando a aprendizagem da matemática ao propiciar um cenário onde novas situações são apresentadas. Introduzindo, também, uma forma de os professores descobrirem, sem constrangimento para os jovens, quais as dificuldades ou os pontos não tão esclarecidos dos conteúdos estudados. Além disso, estimular o uso do raciocínio lógico, já que, após a fase de aprendizagem, os alunos começam a tecer estratégias e elaborar jogadas para vencer o adversário. Além disso, podem ser considerados objetivos:
- Apresentar sugestões de jogos de fácil confecção, agradáveis aos alunos e que possam ser trabalhados em sala de aula, despertando o interesse dos estudantes e auxiliando a aprendizagem da Matemática.
- Aplicar, em turmas de 5ª a 8ª séries, os jogos sugeridos e avaliar de forma subjetiva o envolvimento dos alunos com o jogo, sua aplicabilidade e as capacidades desenvolvidas.
Jogos apresentados:
- Matix;
- Quebra-cabeça: as oito peças travessas;
- Bingo de Operações;
- Jogo dos Trezentos e Dez;
- Jogo das Frações: complete o inteiro;
- Sudoku.
Matix - o jogo dos números inteiros
Conteúdo
- Adição e subtração de números inteiros (Recomendado para turmas de 6ª série)
Objetivos
- Cálculo mental de adição e subtração com os números inteiros.
- Desenvolvimento de estratégias de raciocínio para resolver problemas.
- Fixação de somas algébricas realizando-as com prontidão e entendimento.
Material necessário
- Tabuleiro com 36 quadrados
- 35 peças com números inteiros positivos e negativos e um curinga.
As peças deverão ser identificadas da seguinte maneira:
Uma peça contendo: |
Duas peças contendo: |
+ 6 |
– 10 |
+15 |
– 5 |
a palavra Curinga |
– 4 |
– 3 |
|
– 2 |
|
– 1 |
|
Três peças contendo: |
+ 1 |
Zero |
+ 2 |
+ 3 |
|
+ 4 |
|
+ 7 |
|
Quatro peças contendo: |
+ 8 |
+ 5 |
+10 |
Desenvolvimento
- Número de jogadores: 2
- As peças devem ser posicionadas aleatoriamente no tabuleiro com os números virados para cima.
- No par ou ímpar define-se quem começa a partida.
- O primeiro jogador escolhe se vai jogar na horizontal ou na vertical. A escolha é mantida até o final da partida.
- O primeiro jogador retira o curinga do tabuleiro e, em seguida, um número da mesma linha (se escolheu jogar na horizontal) ou coluna (se preferiu a vertical).
- O segundo só pode retirar sua peça da linha ou da coluna da qual foi tirada a última peça.
- A partida segue assim e termina quando não restarem peças na coluna ou linha da jogada.
- Para determinar o ganhador, soma-se o total de pontos retirados por jogador.
- Vence quem tiver mais pontos.
- Como a meta do jogador é conseguir o maior número de pontos, para tanto, ele deve pensar nas melhores opções de movimento, antevendo os movimentos do adversário, com o objetivo de forçá-lo a ficar com as peças de valor mais baixo, principalmente as negativas.
Jogo extraído da Revista Nova Escola, edição de novembro de 2004, citado por Marangon.
Aplicação
Confeccionamos alguns tabuleiros e peças junto com a professora de Artes.
Para a aplicação desse jogo tivemos que dividir algumas turmas em duas (com auxilio da professora de Ciências), pois o número muito grande de alunos dificulta o trabalho.
O jogo requer bastante atenção, mas se um aluno calcula errado e é prejudicado na jogada, logo percebe e procura melhorar seus cálculos.
Avaliação
Os alunos demonstram muito prazer em participar desse jogo, o que torna mais agradáveis os cálculos com números inteiros, que é tão complicado para a maioria dos alunos de 6ª série.
Quebra-cabeça - As oito peças travessas
Objetivos
- Ajudar a deduzir estratégias - Autoavaliação
Material necessário
- 8 peças, conforme modelo abaixo.
- As peças poderão ser reproduzidas em cartolina, papelão ou madeira.
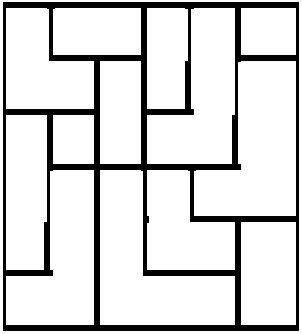
Desenvolvimento
- As oito peças são entregues ao jogador para que ele construa um quadrado perfeito, sem sobrar qualquer peça ou ficar espaço em branco.
- O jogador não deve ver o desenho com o quadrado inicial.
Jogo extraído do livro Jogos para treinar o cérebro (Batllori, 2006).
Aplicação
Primeiramente foi apresentado aos alunos o quebra-cabeça pronto para que tentassem montar. Após várias tentativas foram entendendo e então cada aluno confeccionou seu próprio quebra-cabeça, para desafiar outros colegas.
Avaliação
A maioria dos alunos demonstrou interesse, mas alguns acharam muito complicado e não se empenharam na montagem, querendo logo desistir, dizendo ser impossível.
Bingo de operações
Objetivos
- Dominar completamente as operações com números naturais.
- Treinar e agilizar o cálculo mental.
- Uso correto da régua e medidas.
- Ordem crescente e decrescente dos algarismos.
Material necessário
- Cartela para marcar as operações “cantadas”. Deverá ser feita, individualmente, pelos alunos. Cada qual escolherá 24 números entre 1 e 75.
- O professor deve preparar operações (de acordo com o nível da turma) que tenham resultados de 1 a 75.
Desenvolvimento
- Os números da cartela deverão ser feitos com caneta e não conter rasuras.
- A marcação dos alunos na cartela não poderá esconder os números por eles escolhidos.
- Cada aluno deverá estar de posse da sua cartela e papel para rascunhar as operações, quando necessário.
- O professor sorteará uma operação de cada vez e o aluno que tiver o resultado em sua cartela, deverá marcá-lo.
- Antes do início do jogo deverão ser estabelecidas algumas regras, por exemplo:
- Vence quem fizer uma quina horizontal;
- Vence quem fizer uma quina vertical;
- Vence quem fizer uma quina diagonal;
- Vence quem preencher toda a cartela.
Sugestões de operações
- Várias operações em um só jogo:
1 x 1 = 1 |
2 x 1 = 2 |
3 x 1 = 3 |
2 x 2 = 4 |
1 x 5 = 5 |
2 x 3 = 6 |
7 x 1 = 7 |
2 x 4 = 8 |
3 x 3 = 9 |
2 x 5 = 10 |
11 x 1 = 11 |
3 x 4 = 12 |
96 - 83 = 13 |
2 x 7 = 14 |
3 x 5 = 15 |
8 x 2 = 16 |
17 x 1 = 17 |
3 x 6 = 18 |
65 - 46 = 19 |
4 x 5= 20 |
3 x 7 = 21 |
11 x 2 = 22 |
62 - 39 = 23 |
3 x 8 = 24 |
5 x 5 = 25 |
2 x 13 = 26 |
3 x 9 = 27 |
4 x 7 = 28 |
14 + 15 = 29 |
6 x 5 = 30 |
97 - 66 = 31 |
4 x 8 = 32 |
11 x 3 = 33 |
17 x 2 = 34 |
7 x 5 = 35 |
6 x 6=36 |
99 - 62 = 37 |
19 x 2 = 38 |
63 - 24 = 39 |
8 x 5 = 40 |
86 - 45 = 41 |
7 x 6 = 42 |
19 + 24 = 43 |
11 x 4 = 44 |
9 x 5 = 45 |
23 x 2 = 46 |
98 - 51 = 47 |
6 x 8 = 48 |
7 x 7 = 49 |
5 x 10 = 50 |
24 + 27 = 51 |
47 + 5 = 52 |
17 + 36 = 53 |
9 x 6 = 54 |
11 x 5 = 55 |
8 x 7 = 56 |
43 + 14 = 57 |
33 + 25 = 58 |
36 + 23 = 59 |
6 x 10 = 60 |
40 + 21 = 61 |
59 + 3 = 62 |
9 x 7 = 63 |
8 x 8 = 64 |
13 x 5 = 65 |
48 + 18 = 66 |
84 - 17 = 67 |
95 - 27 = 68 |
83 - 14 = 69 |
7 x 10 = 70 |
96 - 25 = 71 |
8 x 9 = 72 |
95 - 22 = 73 |
81 - 7 = 74 |
25 x 3 = 75 |
- Única operação por jogo:
10 – 9 = 1 |
15 – 13 = 2 |
25 – 22 = 3 |
30 – 26 = 4 |
45 - 40 = 5 |
12 – 6 = 6 |
14 – 7 = 7 |
16 – 8 = 8 |
16 – 7 = 9 |
100 - 90 = 10 |
21 – 10 = 11 |
24 – 12 = 12 |
33 – 20 = 13 |
44 – 30 = 14 |
95 – 80 = 15 |
20 – 4 = 16 |
18 – 1 = 17 |
20 – 2 = 18 |
29 – 10 = 19 |
100 - 80 = 20 |
41 - 20 = 21 |
33 – 11 = 22 |
34 – 11 = 23 |
54 – 30 = 24 |
85 – 60 = 25 |
30 – 4 = 26 |
28 – 1 = 27 |
58 – 20 = 28 |
39 – 10 = 29 |
100 - 70 = 30 |
101 - 70 = 31 |
34 – 2 = 32 |
66 – 33 = 33 |
38 – 4 = 34 |
65 – 30 = 35 |
48 - 12 = 36 |
87 – 50 = 37 |
39 – 1 = 38 |
39 – 0 = 39 |
100 - 60 = 40 |
91 - 50 = 41 |
46 – 4 = 42 |
50 – 7 = 43 |
50 – 6 = 44 |
55 – 10 = 45 |
49 – 3 = 46 |
57 – 10 = 47 |
88 – 40 = 48 |
59 – 10 = 49 |
100 - 50 = 50 |
62 - 11 = 51 |
60 – 8 = 52 |
60 – 7 = 53 |
64 – 10 = 54 |
58 – 3 = 55 |
58 – 2 = 56 |
60 – 3 = 57 |
60 – 2 = 58 |
60 – 1 = 59 |
100 - 40 = 60 |
82 - 21 = 61 |
65 – 3 = 62 |
83 – 20 = 63 |
69 – 5 = 64 |
97 – 32 = 65 |
166 - 100 = 66 |
77 – 10 = 67 |
79 – 11 = 68 |
71 – 2 = 69 |
100 - 30 = 70 |
72 – 1 = 71 |
80 – 8 = 72 |
80 – 7 = 73 |
99 – 25 = 74 |
97 – 22 = 75 |
1 + 0 = 1 |
1 + 1 = 2 |
1 + 2 = 3 |
1 + 2 +1 = 4 |
2 + 3 = 5 |
4 + 2 = 6 |
1 + 6 = 7 |
6 + 2 = 8 |
9 + 0 = 9 |
3 + 7 = 10 |
6 + 5 = 11 |
2 + 10 = 12 |
3 + 7 + 3 = 13 |
7 + 7 = 14 |
6 + 9 = 15 |
12 + 4 = 16 |
8 + 9 = 17 |
6 + 12 = 18 |
11 + 8 = 19 |
8 + 12 = 20 |
1 + 20 = 21 |
10 + 12 = 22 |
11 + 12 = 23 |
19 + 5 = 24 |
10 + 10 + 5 = 25 |
13 + 13 = 26 |
13 + 14 = 27 |
15 + 13 = 28 |
12 + 17 = 29 |
15+ 15 = 30 |
21 + 10 = 31 |
2 + 20 + 10 = 32 |
3 + 11 + 20 = 33 |
12 + 12 + 10 = 34 |
1 + 4 + 30 = 35 |
12 + 12 + 12 = 36 |
20 + 10 + 7 = 37 |
20 + 18 = 38 |
13 + 13 + 13 = 39 |
20 + 10 + 10 = 40 |
11 + 30 = 41 |
12 + 30 = 42 |
12 + 21 = 43 |
12 + 32 = 44 |
10 + 15 + 20 = 45 |
13 + 33 = 46 |
38 + 9 = 47 |
24 + 24 = 48 |
25 + 24 = 49 |
30 + 20 = 50 |
20 + 20 + 10 + 1 = 51 |
40 + 10 + 2 = 52 |
2 + 1 + 50 = 53 |
48 + 6 = 54 |
5 + 50 = 55 |
16 + 40 = 56 |
49 + 8 = 57 |
51 + 7 = 58 |
33 + 26 = 59 |
20 + 20 + 20 = 60 |
59 + 2 = 61 |
12 + 30 + 30 = 62 |
43 + 20 = 63 |
22 + 42 = 64 |
15 + 50 = 65 |
33 + 33 = 66 |
27 + 40 = 67 |
30 + 38 = 68 |
23 + 23 + 23 = 69 |
35 + 35 = 70 |
31 + 40 = 71 |
70 + 2 = 72 |
50 + 23 = 73 |
65 + 9 = 74 |
69 + 6 = 75 |
Aplicação
Na primeira aplicação do jogo as cartelas já vieram prontas, para o melhor entendimento. Realizamos o jogo e os alunos que iam completando linha horizontal, vertical ou diagonal e depois cartela cheia, iam sendo premiados (prêmios simbólicos, como lápis, borracha, caneta etc.).
A partir da segunda aplicação os alunos construíram suas próprias cartelas.
Avaliação
Esse jogo gera um grande entusiasmo, os alunos procuram cada vez resolver com mais rapidez e precisão as operações.
O Jogo dos Trezentos e Dez
Objetivo
- Treinar e agilizar o cálculo mental.
Material necessário
10 |
10 |
10 |
10 |
20 |
20 |
20 |
20 |
30 |
30 |
30 |
30 |
40 |
40 |
40 |
40 |
50 |
50 |
50 |
50 |
60 |
60 |
60 |
60 |
- Dois lápis ou caneta,
- Um diagrama como este:
Desenvolvimento
- Número de jogadores: 2
- Cada jogador escolhe um símbolo para assinalar.
- Cada um dos jogadores escolhe um número do diagrama e o assinala usando seu símbolo.
- Os jogadores se alternam e a cada jogada somam os números assinalados com seu símbolo.
- Cada quadrícula só poderá ser assinalada uma vez.
- Aquele que atingir exatamente 310 pontos será o vencedor.
Observação: O diagrama e o valor total podem variar de acordo com a turma ou o conteúdo a ser trabalhado (por exemplo: decimais, negativos).
Aplicação
Confeccionamos os diagramas com números inteiros positivos e fizemos algumas jogadas. Em seguida construímos os diagramas com números inteiros positivos e negativos para melhor fixação desse conteúdo. A cada jogada alterando as duplas para maior entrosamento.
Avaliação
Esse jogo estimula o cálculo mental, pois os alunos querem jogar rapidamente e ganhar.
Jogo das Frações – Complete o inteiro
Objetivo
- Construção do conceito de frações e operações com frações.
Material necessário
- Confeccionar cartelas com os alunos, em cartolina, papel cartão ou papelão, formado pelo inteiro e por diversas possibilidades de divisões em partes iguais.
Sugestão de tamanho: 18cm X 6cm
1 |
1/2 |
1/2 |
1/3 |
1/3 |
1/3 |
1/4 |
1/4 |
1/4 |
1/4 |
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
Cada cartela deve ser pintada com uma cor diferente das demais e depois recortada nas marcações.
- Confeccionar um dado com as faces fracionárias, iguais às divisões escolhidas.
Desenvolvimento
- Número de jogadores: 2
- Cada jogador deverá ter o seu jogo de cartelas.
- O tabuleiro inicial deve ser o inteiro.
- Um aluno, de cada vez, sorteia o dado e coloca sobre o inteiro a parte sorteada.
- Ganha o jogo o aluno que primeiro completar o inteiro.
- Se a parte sorteada for maior que a que falta para ser completada, o jogador passa a vez, sem colocar nenhuma peça.
Sugestão: Pedir que cada aluno anote em seu caderno as peças conforme for colocando sobre o seu inteiro e ao final efetue a soma.
Aplicação
O jogo foi aplicado em turmas de 6ª série. O material foi confeccionado pelos alunos. Esclarecimento das regras do jogo. Realização do Jogo das Frações, em dupla.
Avaliação
Os alunos puderam colocar oralmente o que aprenderam com o jogo e as dúvidas que surgiram.
Sudoku
Objetivos
- Desenvolver o pensamento crítico e analítico.
- Aprimorar o raciocínio.
Desenvolvimento
- Preencher os espaços em branco com os algarismos de 1 a 9, de modo que cada número apareça apenas uma vez na linha A.
- O mesmo deve acontecer em cada coluna. Nenhum número pode ser repetido e todos os números de 1 a 9 se encontram presentes B.
- Nos quadrados menores (3 x 3), a regra é a mesma: aparecem os números de 1 a 9, mas nenhum se repete (C).
Exemplo:
|
|
(1) (2) (3)
3 |
5 |
4 |
2 |
8 |
7 |
5 |
4 |
8 |
9 |
7 |
3 |
4 |
1 |
7 |
9 |
5 |
2 |
|||||||||||
1 |
7 |
6 |
5 |
4 |
2 |
3 |
8 |
6 |
7 |
2 |
4 |
6 |
9 |
5 |
2 |
8 |
4 |
|||||||||||
4 |
8 |
3 |
7 |
9 |
6 |
7 |
1 |
3 |
4 |
9 |
6 |
7 |
5 |
8 |
4 |
1 |
3 |
|||||||||||
5 |
4 |
2 |
6 |
7 |
3 |
8 |
4 |
9 |
1 |
6 |
2 |
1 |
4 |
9 |
8 |
7 |
3 |
|||||||||||
6 |
1 |
5 |
3 |
2 |
9 |
2 |
6 |
4 |
3 |
1 |
5 |
2 |
8 |
5 |
4 |
1 |
6 |
|||||||||||
8 |
3 |
7 |
9 |
6 |
5 |
7 |
3 |
2 |
5 |
4 |
9 |
5 |
9 |
3 |
1 |
8 |
4 |
|||||||||||
2 |
5 |
7 |
6 |
4 |
3 |
9 |
7 |
5 |
3 |
8 |
4 |
8 |
7 |
1 |
6 |
4 |
9 |
|||||||||||
7 |
3 |
4 |
2 |
5 |
6 |
3 |
2 |
7 |
1 |
5 |
6 |
2 |
6 |
4 |
8 |
3 |
7 |
|||||||||||
4 |
6 |
5 |
3 |
2 |
1 |
4 |
1 |
8 |
2 |
6 |
9 |
1 |
5 |
3 |
9 |
2 |
8 |
(4) (5) (6)
4 |
6 |
9 |
3 |
1 |
2 |
2 |
7 |
5 |
4 |
6 |
8 |
1 |
5 |
7 |
3 |
6 |
2 |
8 |
||||||||||
5 |
9 |
1 |
4 |
8 |
7 |
8 |
5 |
1 |
6 |
9 |
8 |
3 |
4 |
2 |
5 |
7 |
||||||||||||
3 |
1 |
2 |
5 |
9 |
6 |
6 |
4 |
9 |
2 |
3 |
5 |
6 |
2 |
5 |
8 |
3 |
9 |
|||||||||||
8 |
4 |
3 |
2 |
7 |
5 |
5 |
4 |
1 |
8 |
2 |
7 |
6 |
5 |
2 |
8 |
7 |
9 |
|||||||||||
1 |
7 |
5 |
9 |
6 |
8 |
8 |
9 |
4 |
2 |
5 |
1 |
8 |
1 |
7 |
9 |
5 |
2 |
|||||||||||
6 |
5 |
7 |
8 |
9 |
3 |
7 |
2 |
9 |
5 |
8 |
4 |
7 |
2 |
4 |
5 |
8 |
3 |
|||||||||||
5 |
4 |
1 |
7 |
2 |
9 |
2 |
3 |
6 |
8 |
1 |
5 |
9 |
6 |
3 |
7 |
1 |
8 |
|||||||||||
8 |
9 |
1 |
5 |
4 |
3 |
7 |
9 |
6 |
2 |
1 |
7 |
3 |
3 |
7 |
8 |
5 |
9 |
6 |
||||||||||
2 |
9 |
3 |
1 |
5 |
4 |
5 |
7 |
9 |
6 |
8 |
2 |
5 |
6 |
9 |
4 |
3 |
(7) (8) (9)
9 |
7 |
2 |
6 |
4 |
3 |
6 |
3 |
7 |
4 |
9 |
1 |
5 |
7 |
4 |
1 |
9 |
||||||||||||
2 |
3 |
7 |
4 |
5 |
6 |
9 |
4 |
1 |
8 |
5 |
3 |
8 |
2 |
1 |
9 |
3 |
||||||||||||
4 |
1 |
5 |
9 |
7 |
2 |
1 |
8 |
6 |
3 |
4 |
2 |
9 |
7 |
3 |
5 |
6 |
||||||||||||
9 |
5 |
4 |
7 |
8 |
6 |
5 |
8 |
4 |
6 |
3 |
4 |
6 |
1 |
8 |
5 |
|||||||||||||
7 |
6 |
8 |
1 |
9 |
4 |
2 |
4 |
1 |
9 |
6 |
5 |
1 |
6 |
7 |
4 |
3 |
||||||||||||
1 |
4 |
9 |
5 |
2 |
3 |
8 |
6 |
9 |
5 |
1 |
7 |
4 |
7 |
8 |
5 |
4 |
1 |
|||||||||||
7 |
8 |
4 |
9 |
1 |
5 |
1 |
8 |
6 |
3 |
4 |
7 |
8 |
9 |
6 |
3 |
2 |
||||||||||||
6 |
4 |
2 |
5 |
7 |
9 |
7 |
6 |
5 |
2 |
9 |
1 |
6 |
7 |
5 |
9 |
8 |
||||||||||||
5 |
9 |
1 |
7 |
6 |
4 |
3 |
2 |
4 |
7 |
8 |
5 |
9 |
3 |
4 |
1 |
6 |
(10) (11) (12)
5 |
1 |
9 |
3 |
4 |
9 |
7 |
8 |
5 |
5 |
4 |
9 |
8 |
1 |
|||||||||||||||
9 |
1 |
7 |
8 |
2 |
5 |
7 |
1 |
6 |
1 |
2 |
3 |
|||||||||||||||||
7 |
3 |
2 |
6 |
9 |
4 |
6 |
5 |
8 |
6 |
9 |
3 |
5 |
||||||||||||||||
8 |
5 |
4 |
3 |
6 |
9 |
4 |
8 |
5 |
6 |
3 |
9 |
8 |
||||||||||||||||
7 |
6 |
8 |
1 |
4 |
1 |
7 |
4 |
2 |
8 |
1 |
9 |
6 |
||||||||||||||||
4 |
2 |
1 |
5 |
8 |
8 |
5 |
4 |
3 |
9 |
3 |
6 |
2 |
||||||||||||||||
2 |
1 |
9 |
3 |
7 |
3 |
4 |
6 |
5 |
3 |
9 |
2 |
6 |
||||||||||||||||
1 |
7 |
5 |
6 |
4 |
1 |
2 |
8 |
7 |
7 |
4 |
8 |
5 |
1 |
|||||||||||||||
3 |
9 |
7 |
8 |
6 |
6 |
9 |
5 |
4 |
9 |
5 |
3 |
(13) (14) (15)
6 |
7 |
8 |
1 |
5 |
1 |
9 |
3 |
8 |
2 |
9 |
5 |
1 |
2 |
|||||||||||||||
8 |
2 |
1 |
6 |
3 |
6 |
8 |
1 |
4 |
4 |
7 |
5 |
1 |
||||||||||||||||
1 |
3 |
2 |
6 |
8 |
2 |
7 |
4 |
8 |
1 |
5 |
1 |
6 |
5 |
3 |
||||||||||||||
4 |
6 |
9 |
1 |
3 |
1 |
4 |
2 |
3 |
8 |
7 |
5 |
2 |
4 |
|||||||||||||||
5 |
6 |
8 |
7 |
2 |
8 |
1 |
3 |
9 |
4 |
2 |
8 |
1 |
3 |
|||||||||||||||
3 |
8 |
1 |
7 |
4 |
7 |
9 |
5 |
4 |
2 |
4 |
3 |
7 |
6 |
|||||||||||||||
1 |
7 |
9 |
2 |
8 |
6 |
8 |
5 |
4 |
1 |
3 |
6 |
7 |
9 |
|||||||||||||||
8 |
2 |
4 |
3 |
5 |
3 |
4 |
9 |
7 |
6 |
7 |
8 |
9 |
1 |
|||||||||||||||
5 |
8 |
1 |
2 |
9 |
8 |
7 |
3 |
6 |
5 |
9 |
1 |
7 |
8 |
(16) (17) (18)
1 |
5 |
6 |
3 |
4 |
5 |
9 |
8 |
1 |
4 |
5 |
3 |
2 |
6 |
|||||||||||||||
3 |
9 |
4 |
8 |
3 |
9 |
4 |
8 |
5 |
2 |
8 |
6 |
9 |
3 |
|||||||||||||||
2 |
3 |
1 |
6 |
6 |
1 |
2 |
4 |
3 |
6 |
8 |
4 |
5 |
2 |
|||||||||||||||
2 |
4 |
6 |
1 |
1 |
5 |
3 |
4 |
6 |
8 |
4 |
1 |
5 |
6 |
|||||||||||||||
5 |
2 |
9 |
3 |
4 |
8 |
1 |
5 |
7 |
3 |
1 |
2 |
4 |
7 |
|||||||||||||||
4 |
1 |
7 |
9 |
9 |
8 |
6 |
3 |
1 |
6 |
4 |
9 |
1 |
8 |
|||||||||||||||
2 |
4 |
8 |
1 |
4 |
2 |
6 |
8 |
5 |
8 |
3 |
7 |
1 |
4 |
|||||||||||||||
9 |
4 |
7 |
8 |
8 |
6 |
3 |
1 |
2 |
7 |
6 |
2 |
1 |
8 |
|||||||||||||||
7 |
9 |
1 |
3 |
5 |
2 |
4 |
1 |
7 |
1 |
4 |
8 |
7 |
2 |
Aplicação
Cada aluno recebeu uma cartela de Sudoku com o mesmo nível de dificuldade, mas com numerais diferentes para que não copiassem.
Avaliação
O jogo foi explicado e alguns alunos acharam muito difícil. Com o desenvolvimento do jogo, e após alguns dicas dos colegas tornou-se possível a participação de todos.
Considerações finais
Foi possível observar que o trabalho com jogos, nas aulas de Matemática, aumentou a motivação fazendo com que muitos alunos passassem a ver as aulas de Matemática como uma aula prazerosa, sem se focar nas dificuldades, desenvolvendo, assim, naturalmente, o raciocínio lógico.
Dessa maneira, entende-se que o trabalho tem boa aplicabilidade e pode ser utilizado como parâmetro inicial para a utilização de jogos nas aulas. Entretanto, a atuação do professor não deve limitar-se aos jogos sugeridos, mas devem ser buscados novos jogos que se adéquem ao perfil dos alunos e ao conteúdo estudado.
Referências
BATLLORI, Jorge. Jogos para treinar o cérebro. Trad. Fina Iñiguez. São Paulo: Madras, 2006.
BORIN, Júlia. Jogos e resolução de problemas: uma estratégia para as aulas de Matemática. São Paulo: IME/USP, 1996.
BRASIL. MEC. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1998.
FERRAREZI, Luciana Aparecida. Criando novos tabuleiros para o jogo Tri-Hex e sua validação didático-pedagógica na formação continuada de professores de Matemática: uma contribuição para a Geometria das séries finais do Ensino Fundamental. Dissertação: (Mestrado), Instituto de Geociências e Ciências Exatas, Universidade Estadual Paulista, 2005.
GROENWALD, Claudia Lisete Oliveira; TIMM, Ursula Tatiana. Utilizando curiosidades e jogos matemáticos em sala de aula. Terra Educação. Disponível em: http://paginas.terra.com.br/educacao/calculu/artigos/professores/utilizando jogos.htm. Acesso em: 15 jun. 2007.
LIMA, Elvira Cristina de Souza. Algumas questões sobre o desenvolvimento do ser humano e a aquisição de conhecimentos na escola. In: PARANÁ. Currículo Básico para a Escola Pública do Estado do Paraná. 3ª ed. Curitiba: SEED, 2003. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/portal/institucional/def/pdf/curriculo_basico_escola_pub_pr.pdf. Acesso em: 13 jul. 2007.
MARANGON, Cristiane. Um jogo para treinar o cálculo mental. Revista Nova Escola, São Paulo, nº 177, p. 58-59, nov. 2004.
TAHAN, Malba. Didática da Matemática. São Paulo: Saraiva, 1965.
Publicado em 13 de setembro de 2022
Como citar este artigo (ABNT)
CIRÍACO, Flávia Lima. Utilizando jogos para ensinar Matemática. Revista Educação Pública, Rio de Janeiro, v. 22, nº 34, 13 de setembro de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/34/utilizando-jogos-para-ensinar-matematica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

