O ensino de congruência na Educação Básica
Keidna Cristiane Oliveira Souza
Graduada em Matemática (UFT), mestra e doutora em Matemática (UnB), professora da UFT - câmpus Arraias/TO
Jucélia Ferreira de Sousa
Graduada em Matemática (UFT), mestra em Matemática (Profmat/UFT), doutoranda em Matemática (UnB), professora da rede municipal de Educação de Campos Belos/GO
Eudes Antonio Costa
Graduado em Matemática (UFG), mestre em Matemática (UFG), doutor em Matemática (UnB), professor da UFT - câmpus Arraias/TO
Trazemos, neste trabalho, o relato do desenvolvimento deste projeto de intervenção pedagógica que buscou amenizar as dificuldades apresentadas pelos estudantes do 8º ano, em Matemática, em particular, na divisão euclidiana. Dessa forma, realizou-se uma atividade de revisão diferenciada que fez parte do nosso trabalho de pesquisa na elaboração da dissertação de Mestrado (Sousa, 2019), cujo objetivo era aplicar a aritmética dos restos ou, simplesmente, a congruência, como ferramenta metodológica para o desenvolvimento do raciocínio lógico e do letramento matemático, habilidades apontadas pela Base Nacional Comum Curricular (BNCC) como uma competência específica da Matemática para o Ensino Fundamental, a saber, “desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo” (Brasil, 2017, p. 267).
Antes de pormenorizar a prática pedagógica realizada no projeto de intervenção é necessário que se trate da base teórica orientadora dessa prática como vetor para a reflexão construída. Na segunda seção, apresentamos um mapeamento da literatura, situando o momento educacional brasileiro e a nossa experiência em sala de aula, com as referências e os fundamentos da pesquisa. Na terceira seção, comentamos os fundamentos teóricos e conceituais que sustentam a proposta, como solicita a BNCC. Nas seções seguintes, apresentamos e detalhamos o projeto, discutindo as intervenções realizadas dentro do ambiente escolar. Na sexta seção, alguns resultados dessas intervenções são apresentados.
Revisão de literatura
O alicerce da Aritmética dos Restos (congruência módulo m) é a divisão euclidiana que consta na matriz curricular do Ensino Fundamental, mais especificamente do 6º ano. Assim, abordar a aritmética dos restos não exigirá uma Matemática além da prevista nesta etapa de ensino. Todavia, há uma discrepância acerca das habilidades esperadas, de acordo com o relatório do Sistema de Avaliação da Educação Básica (SAEB) de 2017.
No 5º ano [...], o nível de aprendizagem médio do país ainda se situa no limite inferior do nível básico, conforme interpretação do MEC (nível 4 de 10). [...] 9° ano cerca de 70% dos estudantes que participaram do SAEB 2017 apresentaram aprendizagem insuficiente em Matemática. [...] 3ª série [...] apenas cerca de 4,5% dos estudantes do país que participaram do SAEB apresentaram aprendizagem adequada (níveis 7 a 10) (Brasil, 2018, p. 26-58).
Esse resultado retrata o que vivenciamos em sala de aula, pois percebemos claramente as dificuldades de alguns discentes, mesmo com o domínio das operações elementares em Matemática (adição e multiplicação com números inteiros). Muitos estudantes só conseguem resolver operações com o auxílio da calculadora e sua utilização que, como ferramenta didática, não é aconselhável. Registramos ainda a aplicação de uma atividade diagnóstica, em turmas do 6º ao 8º anos, no início do ano letivo de 2019, envolvendo apenas operações elementares. Constatamos que quase 50% deles não conseguiam resolver situações-problemas ou questões de manipulação (Roque, 2015, p. 48).
No início de 2019, fizemos um mapeamento rápido da literatura no Brasil acerca do tema, realizado no motor de busca Google Scholarcom os termos “Aritmética dos Restos” e “Ensino”, excluindo os termos “Geometria” e “congruência de triângulos". Verificamos uma vasta literatura voltada ao tema, pois esta solicitação devolveu mais de 5.000 trabalhos de pesquisa (artigos em periódicos, artigos em conferências, dissertações e teses, dentre outros). Isso mostrou que o assunto está bastante aquecido. Após leitura crítica dos resultados e aplicação de critérios de exclusão (duplicações, não adequação ao tema), algumas pesquisas de pós-graduação e artigos foram selecionadas como representativas desse corpo de produção científica. Todas tratam da aplicação da aritmética dos restos no Ensino Fundamental, por meio de “truques” e/ou a preparação para as olimpíadas de Matemática (Obmep, 2021). Recentemente (a partir de 2017) diversas dissertações de mestrado, produzidas no Brasil, notadamente no programa Profmat, exploram a Aritmética dos Restos como instrumento de mediação pedagógica para a apresentação ou a fixação de conceitos relacionados à divisibilidade ou aos processos cíclicos, introduzindo formalmente a definição de congruência entre dois números inteiros.
Materiais e métodos
Em vista às dificuldades apresentadas pelos estudantes em relação à Matemática, em particular à divisão euclidiana entre números inteiros, por meio de uma atividade diagnóstica e dos relatórios SAEB (Brasil, 2018) ou do Programa Internacional de Avaliação de Estudantes (PISA) (Brasil, 2012), constatamos a importância desse conteúdo no progresso acadêmico do educando, buscando estabelecer um elo entre o cotidiano e a Matemática escolar. A abordagem facilitou o entendimento e, consequentemente, o interesse dos estudantes pela Matemática, desenvolvendo, dessa forma, o “letramento matemático” necessário para atuar em sociedade, como determina a BNCC (Brasil, 2017).
Coube ao "príncipe dos matemáticos”, Carl Friedrich Gauss (1777-1855), o marco inicial da teoria dos números atual, em particular, na notação e em alguns resultados da aritmética dos restos. Dentre as várias obras publicadas por Gauss, destacamos a Disquisitiones Arithmeticae (Investigações Aritméticas), escrita em 1798 (e publicada em 1801), que se tornou um clássico da literatura matemática (Boyer, 1996).
Essa obra célebre é a principal responsável pelo desenvolvimento da linguagem e notação do ramo da teoria dos números conhecido como álgebra das congruências que fornece um exemplo de classes de equivalência. A exposição começa com a definição: se um número a divide a diferença entre dois números b e c, então b e c dizem-se congruentes, de outra forma incongruentes; e a chama-se o módulo. [...] A notação que Gauss adotou foi a que se usa hoje (Boyer, 1996, p. 371).
Entendemos que a História da Matemática pode fundamentar a construção do conhecimento matemático, bem como as estratégias desenvolvidas para este ensino.
O modo de escrever o encadeamento das definições, dos teoremas e das demonstrações é, desde muitos séculos, uma preocupação fundamental da matemática. No entanto, não podemos deixar de perceber uma diferença crucial entre a ordem lógica da exposição, o modo como um texto matemático é organizado para ser apresentado, e a ordem da invenção, que diz respeito ao modo como os resultados matemáticos se desenvolveram (Roque, 2015, p. 12).
Para motivar o estudo de congruência e despertar o interesse dos estudantes, apresentamos “mágicas” ou “truques”, com o objetivo de incentivar a assimilação do conteúdo pelos discentes. Conceitualmente, buscamos nortear os discentes na elaboração, na construção e na obtenção de um conhecimento ativo. Assim, o professor “daria oportunidade aos alunos de descobrirem por si mesmos as coisas a serem aprendidas” (Polya, 1987). Vale ressaltar o quanto o projeto foi orientado e motivado por Polya:
Dê aos seus alunos não apenas informações, mas know-how, atitudes mentais, o hábito de trabalho metódico. Já que know-how é mais importante em Matemática do que informação, a maneira como você ensina pode ser mais importante nas aulas de matemática do que aquilo que você ensina (Polya, 1987).
Contextualização: Matemática e o projeto de intervenção
Aqui, consideramos o conjunto dos números inteiros designado por:
Z = {..., - (n + 1), - n, ..., - 3, - 2, - 1, 0, 1, 2, 3, ..., n, n + 1, ...}
provido das operações de adição e multiplicação a relação “menor que” e satisfazendo algumas propriedades (leis básicas da aritmética).
Observemos que 2022 = 1 x 1798 + 224. Dados dois inteiros a e b, em geral é possível encontrar os inteiros q e r tal que a = q x b + r. Esse resultado é devido a “Euclides”, conhecido como algoritmo da divisão de Euclides. Formalmente temos:
Teorema 1. Para quaisquer a e b dois números inteiros com b  0. Existem dois únicos números inteiros q e r tais que
0. Existem dois únicos números inteiros q e r tais que
a = b x q + r; com 0
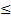 r
r
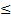 | b |.
| b |.
Salientamos que os elementos a; b; q e r são chamados de divisor, dividendo, quociente e resto, respectivamente.
A Aritmética dos Restos (ou problemas-situações), com situação cíclica, é pouco explorada no Ensino Fundamental e no Ensino Médio. Em alguns casos, se reduz a problemas com horas ou dias da semana. Mesmo assim, não aborda (conceitualmente) a definição e a propriedade de congruência. Para nossa surpresa, no Exame Nacional do Ensino Médio (Enem), 2019, apareceu a seguinte questão:
Problema 2. (INEP, 2019) Após o Fórum Nacional Contra a Pirataria (FNCP) incluir a linha de autopeças em campanha veiculada contra a falsificação, as agências fiscalizadoras divulgaram que os cinco principais produtos de autopeças falsificados são: rolamento, pastilha de freio, caixa de direção, catalisador e amortecedor (Disponível em: www.oficinabrasil.com.br. Acesso em: 25 ago. 2014 - adaptado).
Após uma grande apreensão, as peças falsas foram cadastradas utilizando-se a codificação: 1: rolamento, 2: pastilha de freio, 3: caixa de direção, 4: catalisador e 5: amortecedor.
Ao final obteve-se a sequência:
5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, ...
que apresenta um padrão de formação que consiste na repetição de um bloco de números. Essa sequência descreve a ordem em que os produtos apreendidos foram cadastrados. O 2.015º item cadastrado foi:
A rolamento.
B catalisador.
C amortecedor.
D pastilha de freio.
E caixa de direção.
Para apresentar a Aritmética dos Restos aos estudantes e explorar algumas propriedades, também utilizamos problemas da Olimpíadas Brasileira de Matemática das Escolas Públicas (Obmep) como motivador ou problema-disparador. Iniciamos com:
Problema 3. (Prova da Obmep, 2012) Um quadrado de lado com 1cm roda em torno de um quadrado de lado com 2cm, como na figura, partindo da posição inicial e completando um giro cada vez que um de seus lados fica apoiado em um lado do quadrado maior. Qual das figuras a seguir representa a posição dos dois quadrados após os 2.012 giros?
Resolução. Em sala de aula utilizamos de dois quadrados: um maior (preto) e outro menor (amarelo); fizemos o movimento descrito pela figura. Analisando coletivamente o movimento (giro) do quadrado menor em torno do maior, verificamos que, após oito giros sucessivos, o quadrado menor retorna à sua posição inicial
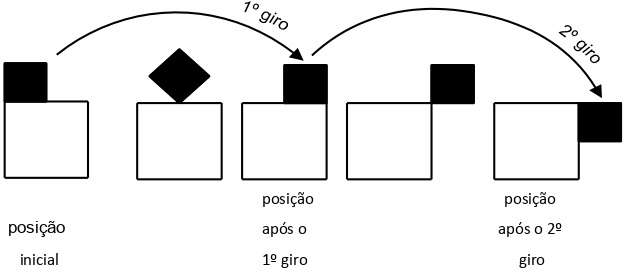
Figura 1: Giros do quadrado menor
Fonte: Obmep, 2012, p. 2.
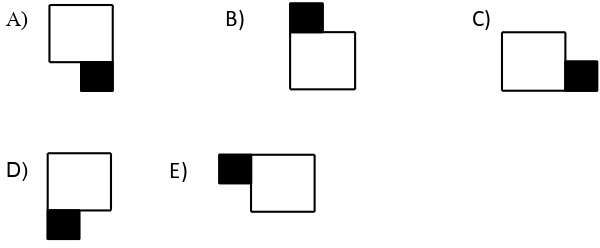
Figura 2: Resultado depois de 2.012 giros
Fonte: Obmep, 2012, p. 2.
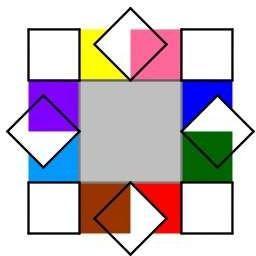
Figura 3: Busca pela resolução
Fonte: Roque, 2015, p. 38.
Como 2012 = 8 x 251 + 4, após os 2012 giros, o quadrado menor terá dado 251 voltas completas no quadrado maior e mais quatro giros, parando na posição da alternativa A. Notamos que não houve a necessidade de rodar o quadrado menor 2012 vezes. Necessitamos, portanto, apenas do resto da divisão de 2012 por 8.
Apresentamos aos estudantes outros problemas.
Problema 5. (Banco de questões Obmep, 2006, p. 56) Considere A, B, C, D, E, F, G e H fios de apoio que uma aranha usa para construir sua teia, conforme mostra a figura. A aranha continua seu trabalho. Sobre qual fio de apoio estará o número 118?
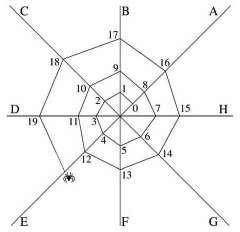
Figura 4: Posição da aranha
Fonte: Obmep, 2006, p. 56.
-
A) B B) D C) E D) G E) H
Após explorarmos (socialização e discussão sobre) as resoluções dos problemas apresentamos:
Definição. Seja m > 1 um número natural. Diremos que dois números inteiros a e b são congruentes módulo m se os restos de sua divisão euclidiana por m são iguais. Quando os inteiros a e b são congruentes módulo m, escreve-se a b mod. m. Quando a e b não são congruentes módulo m, podemos dizer também incongruentes, escreve-se a 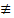 b mod. m.
b mod. m.
Como exemplo podemos verificar se 15 é ou não côngruo a 8 (módulo 7), para tal fazemos a divisão euclidiana de 15 e de 8 por 7, temos que 15 dividido por 7 tem quociente 2, com resto 1, isto é 15 = 2 x 7 + 1, enquanto 8 dividido por 7 tem quociente 1 e resto 1, ou seja, 8 = 1 x 7 + 1. Comparando os dois restos, percebemos que ambos são iguais a 1. Com isso dizemos que 15 é congruente a 8.
Retomando a resolução do problema 3: como 2008 = 8 x 251 + 0, segue que 2008
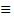 0 (mod. 8) e assim 2012
0 (mod. 8) e assim 2012
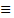 4 (mod. 8). De modo similar, no problema 5, na resolução os estudantes constataram que 112 = 14 x 8 + 0, ou seja, 112
4 (mod. 8). De modo similar, no problema 5, na resolução os estudantes constataram que 112 = 14 x 8 + 0, ou seja, 112
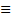 0 (mod. 8) e assim 118
0 (mod. 8) e assim 118
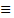 6 (mod. 8), momento em que apontam corretamente o fio em que a aranha estará.
6 (mod. 8), momento em que apontam corretamente o fio em que a aranha estará.
Em sala, apresentamos (definimos) as operações de adição e multiplicação na aritmética dos restos.
Desenvolvimento e descrição das atividades
O projeto de intervenção pedagógica Congruência no Ensino Fundamental foi aplicado no 8º ano do Ensino Fundamental de uma escola da rede municipal da Cidade de Campos Belos/GO. Os estudantes apresentavam dificuldades em conteúdos básicos de Matemática. Esse resultado foi constatado por meio de uma atividade diagnóstica (Roque, 2015, p. 47) composta por dez questões, envolvendo operações elementares e aplicadas em turmas do 6º, 7º e 8º anos, conforme mostra a Tabela 1.
Tabela 1: Resultado da atividade diagnóstica
Número de acertos |
Quantidade de alunos |
Percentual (%) |
0 |
16 |
37, 2 |
1 |
4 |
9, 3 |
2 |
6 |
13, 9 |
3 |
3 |
6, 9 |
4 |
3 |
6, 9 |
5 |
2 |
4, 6 |
6 |
3 |
6, 9 |
7 |
3 |
6, 9 |
8 |
2 |
4, 6 |
9 |
0 |
0, 0 |
10 |
1 |
2,3 |
Fonte: Roque, 2015, p. 47.
Esses dados nos remetem a uma situação desconfortável. Constatamos que é inferior a 50% a quantidade de estudantes que conseguiram resolver “operações básicas” de Matemática, envolvendo apenas números inteiros. Considerando um aproveitamento igual ou superior a 50% das questões, temos um total de apenas 11 estudantes. Esse fato está em desacordo com as habilidades propostas e esperadas para esse nível de escolaridade, segundo a BNCC. Diante da situação, fizemos uma introdução conceitual e histórica sobre a aritmética dos restos. Ressaltamos que em nossa prática pedagógica é importante que os estudantes busquem, tentem e procurem pela resolução dos problemas propostos em sala de aula de forma empírica. Algumas vezes, por tentativa e erro, é necessário que se incentive a fazer consultas para além do livro didático. Assim, a metodologia utilizada na pesquisa-ação foi qualitativa (ambiente escolar), pois os estudantes estavam envolvidos na exploração da estratégia para a solução dos problemas propostos.
Os encontros, durante o desenvolvimento do projeto, ocorreram concomitantemente ao horário regular escolar, nas atividades da disciplina de Matemática. No primeiro encontro, utilizamos duas aulas de 48 minutos cada. No segundo e no terceiro encontros foram três aulas cada. No quarto, quinto e sexto encontros, duas aulas cada. Finalizamos com o sétimo encontro com três aulas. Faremos a seguir uma descrição sucinta de cada encontro.
1º Encontro
Realizamos atividades abordando os conceitos de múltiplos e divisores de um número inteiro positivo, primos menores que 20 e decomposição de alguns números em fatores primos, seguidas da oficina de resolução de exercícios.
2º Encontro
Exibimos um cartaz com números entre 1 e 2019 e pedimos aos alunos que listassem os números divisíveis pelos primos menores que 20. Assim, provocamos os alunos a apontarem algumas regras de divisibilidade, fazendo suas anotações para consulta da veracidade.
3º Encontro
Exploramos a divisão euclidiana motivada por situações problemas, a saber, como dividir três queijos entre duas crianças ou como dividir vinte e sete livros entre quatro pessoas. Finalizamos o encontro com a oficina de resolução de problemas.
4º Encontro
Realizamos atividades que envolvem o maior divisor comum (m.d.c.), usando o algoritmo de Euclides, eficiente para números grandes (Jurkiewicz, 2019).
5º Encontro
Apresentamos situações problemas que envolvem o m.d.c. entre dois números inteiros. Como aplicação, resolvemos algumas equações diofantinas.
6º Encontro
Realizamos atividades exploratórias com equações diofantinas, modeladas no cotidiano dos estudantes, instigando a resolução (heurística) das equações. Destacamos que a resolução foi socializada no quadro branco. Apresentamos também o padrão que existe nas soluções, isto é, quando uma variável aumenta, a outra diminui. Ainda neste encontro, propusemos que os discentes, em grupo, criassem situações problema que foram resolvidas e socializadas no quadro por eles (Cadar; Dutenhefner, 2021).
7º Encontro
A introdução à Aritmética dos Restos apresentou, já no 2° encontro, o desafio do Problema 3, quando tomamos e apresentamos alguns conceitos de congruência. Em seguida, exploramos algumas situações problema, bem como salientamos algumas aplicações (com justificativa) que se encontram em nosso cotidiano, tais como CPF, código de barras e código internacional de livros (Rodrigues, 2018).
Em cada encontro, deixávamos algum desafio, exibindo algum truque. Por exemplo:
Problema 7: O nove misterioso (Hefez, 2016, p. 64).
Peça para alguém escolher, em segredo, um número natural com, pelo menos, três algarismos distintos. Peça ainda para que efetue uma permutação qualquer dos seus algarismos, obtendo um novo número e subtraia o menor do maior dos dois números. Finalmente, peça ao seu parceiro de jogo para reter um dos algarismos diferentes de zero desse novo número para divulgar os restantes. É possível adivinhar o algarismo retido!
Problema 8: A peça do dominó (Bastos, 2005, p. 26).
Apresentamos todas as peças do jogo de dominó e, de costas, solicitamos a um estudante que escolhesse uma peça. Em seguida, pedimos que escolha um dos lados da peça e que siga as indicações:
(1) Multiplicar por 6 o número de pintas que existem no lado que escolheu.
(2) Ao resultado obtido, adicionar o número total de pintas que existem na peça.
(3) Dizer o resultado obtido.
De acordo com o resultado, adivinha qual foi a peça escolhida pelo voluntário?
Resultado e discussão
Nos encontros, percebemos uma participação mais efetiva dos estudantes, pois muitas atividades despertaram o interesse e a curiosidade deles. Em alguns momentos, registramos até uma euforia, por perceberem ou verificarem alguma regra de divisibilidade, além da melhora na concentração e um maior interesse dos estudantes. Em outros momentos, vemos que parte dos alunos apresentaram dificuldades em relação à divisão euclidiana ou em compreender que o “m.d.c.” resolvia aquela situação problema ou que a modelação da situação problema era uma equação diofantina. Mesmo diante de tais dificuldades, acreditamos que o interesse estava relacionado à abordagem com situações problema contextualizadas à vivência dos discentes, fazendo um elo entre a Matemática acadêmica e o cotidiano dos discentes. Ressaltamos que a utilização de “truques” (ou desafios) despertava a curiosidade deles, uma empolgação e uma surpresa quando descobriram que a Matemática “existia” quando entendiam a aplicação da congruência naquela mágica (truque).
Ao trabalharmos problemas da prova ou do banco de questões da Obmep, alguns estudantes ficaram surpresos, pois, ao não se classificarem para a segunda fase da olimpíada, imaginavam que na competição apareceriam questões dificílimas e avançadas, as chamadas “coisas de outro mundo”, em Matemática.
Ao final do projeto, constatamos que o domínio do conhecimento acerca da aritmética dos restos facilitou a autonomia e a segurança dos discentes em questões que envolviam a divisibilidade. Assim, ao usarmos congruência para fazer “adivinhações”, “mágicas” e “truques”, muitos reproduziam essas atividades com colegas da escola ou familiares. Desse modo, o maior interesse em participar das aulas estava em aprender as mágicas.
Vejamos, por exemplo, o resultado por bimestre acerca do rendimento escolar das turmas que fizeram a atividade diagnóstica:
Tabela 2: Percentual de alunos abaixo da média por bimestre
Bimestre (ano letivo 2019) |
Todos que fizeram diagnóstico (%) |
1º |
48,8 |
2º |
41,8 |
3º |
34,8 |
4º |
10 |
Fonte: Secretaria da escola.
O projeto Congruência no Ensino Fundamental foi aplicado no decorrer do 2º bimestre e os dados acima ilustram uma queda de 83%, ou seja, de 5, se compararmos o 2° com o 3° bimestres, entre os que participaram do projeto, enquanto nas outras turmas que não participaram do projeto este percentual foi de apenas 16, ou seja, de 7%. Em relação ao 3º e 4º bimestres, a queda do número de notas abaixo da média dos alunos que participaram do projeto foi de 100% e nas outras turmas, de 71%, ou seja, de 2. Comparamos, ainda, o resultado em Matemática dessas turmas.
Tabela 3: Resultado em Matemática no ano letivo de 2019
Aproveitamento |
Não participaram do projeto (%) |
Participaram do projeto (%) |
Reprovados |
10 |
0 |
Aprovados |
90 |
100 |
Fonte: Secretaria da escola.
Registramos que os estudantes que participaram do projeto foram aprovados, com compreensão e assimilação do conteúdo abordado.
Considerações finais
Aqui relatamos nossa estratégia ao abordar o ensino de congruência como atividade para revisar a divisão euclidiana e a divisibilidade. De um lado tínhamos a relevância do assunto e, por outro, o insucesso de muitos discentes (cerca de 50%) na atividade de diagnóstico aplicada. Conforme os documentos oficiais, eles já deveriam possuir habilidades compatíveis. Naquele momento, nos propusemos a trabalhar apenas uma turma do 8º ano, procurando amenizar algumas dificuldades encontradas pelos discentes.
Em sala de aula, valorizamos a participação ativa dos estudantes, instigando-os em suas “conjecturas”, deixando um tempo para pensar e outro para elaborar um argumento que validasse a proposta de resolução. Em outros momentos, questionamos se aquela “conjectura” valia sempre. Quando aparecia um contraexemplo, percebiam que não estava correto o que propunham. Uma dificuldade inicial era mostrar o que era argumentação, por casos particulares e um raciocínio geral, com linguagem e notação apropriadas. Por exemplo, os estudantes afirmam corretamente que pares são os números terminados em 0, 2, 4, 6 ou 8, no entanto, poucas vezes usam a notação 2n para qualquer n inteiro.
Após a aplicação do Enem 2019, apresentamos o problema 2 às turmas de 6º, 7º e 8º ano. Tivemos a mesma postura, leitura e análise coletiva. Apenas na turma em que desenvolvemos o projeto, com menor esforço, os estudantes constataram um período cíclico no registro das peças e apontaram, corretamente, a resolução. Nas outras, tivemos que apontar claramente o período nos registros e indicar a divisão euclidiana a ser realizada.
Referências
BASTOS, Ilda M. S. Magia matemática com os números. Dissertação (Mestrado em Matemática para professores) - Universidade de Aveiro, Aveiro, 2005. Disponível em: https://ria.ua.pt/bitstream/10773/16822/1/Magia%20Matem%C3%A1tica%20com%20Numeros.pdf. Acesso em: 20 jan. 2019.
BRASIL. Base Nacional Comum Curricular. Brasília: Ministério da Educação, 2017. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 04 out. 2019.
______. Relatório Nacional PISA 2012: resultados brasileiros. Brasília: INEP, 2012. Disponível em: http://download.inep.gov.br/acoes_internacionais/pisa/resultados/2014/relatorio_nacional_pisa_2012_resultados_brasileiros.pdf. Acesso em: 11 jul. 2019.
______. Exame Nacional do Ensino Médio. Brasília: INEP, 2019. Disponível em: https://inep/enem/provas-gabaritos-enem-2019.htm. Acesso em: 20 nov. 2019.
______. SAEB - evidências da edição 2017. Brasília: INEP, 2018. Disponível em: http://portal.mec.gov.br/index.php?option=com_docman&view=download&alias=94161saeb2017-versao-ministro-revfinal&category_slug=agosto-2018-pdf&Itemid=30192. Acesso em: 23 out. 2019.
BOYER, Carl B. História da Matemática. 2ª ed. São Paulo: Edgard Blucher, 1996.
CADAR, Luciana; DUTENHEFNER, Francisco. Encontros de aritmética. Apostila do PIC-Obmep. 2021. Disponível em: www.obmep.org.br. Acesso em: 05 maio 2021.
COSTA, Eudes Antonio; SANTOS, Ronaldo Antônio. Números: dos naturais aos reais. XXIII SEMANA DO IME/UFG, 2008. Proceedings... Disponível em: https://semanadoime.ime.ufg.br/up/34/o/min_eudes_ronaldo.pdf. Acesso em: 01 maio 2021.
DOMINGUES, Hygino Hugueros. Fundamentos de Aritmética. São Paulo: Atual, 1991.
HEFEZ, Abramo. Iniciação à aritmética. Apostila do PIC-OBMEP. 2021. Disponível em: www.obmep.org.br. Acesso em: 20 mar. 2019.
______. Aritmética. 2ª ed. Rio de Janeiro: SBM, 2016. Coleção Profmat.
JURKIEWICZ, Samuel. Divisibilidade e números inteiros: introdução à Aritmética Modular. Apostila do PIC-OBMEP. 2019. Disponível em: www.obmep.org.br. Acesso em 01 maio 2019.
NERY, Chico. Revisitando a aritmética. Revista do Professor de Matemática, v. 80, 2013. Disponível em: http://www.rpm.org.br. Acesso em: 10 maio 2019.
OBMEP. Olimpíada Brasileira de Matemática das Escolas Públicas. Disponível em: www.obmep.org.br. Acesso em 05 out. 2021.
POLYA, George. Dez mandamentos para professores. Revista do Professor de Matemática, v. 10, 1987. Disponível em: http://www.rpm.org.br. Acesso em 26 out. 2019.
RODRIGUES, Luciana M. D. A. Resolução de problemas aplicados ao cotidiano: uma metodologia alternativa para o ensino de divisibilidade e de congruência modular. Nexus Mathematicæ, v. 1, p. 99-108, 2018.
ROQUE, Tatiane. História da Matemática: uma visão crítica, desfazendo mitos e lendas. Rio de Janeiro: Zahar, 2015.
SOUSA, Jucélia F. Aplicação da congruência na Educação Básica. Dissertação (Mestrado Profissional) – Universidade Federal do Tocantins, Arraias, 2019.
Publicado em 11 de outubro de 2022
Como citar este artigo (ABNT)
SOUZA, Keidna Cristiane Oliveira; SOUSA, Jucélia Ferreira de; COSTA, Eudes Antonio. O ensino de congruência na Educação Básica. Revista Educação Pública, Rio de Janeiro, v. 22, nº 38, 11 de outubro de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/38/o-ensino-de-congruencia-na-educacao-basica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

