Histórias em Quadrinhos em sala de aula: uma proposta com o Teorema de Pitágoras
Higor Soares Majoni
Mestre em Educação em Ciências e Matemática (Ifes)
Ligia Arantes Sad
Doutora em Educação (Unesp)
Considerações iniciais
As histórias em quadrinhos sempre foram um artigo sedutor, em especial para o público infantojuvenil. Por muito tempo, encontradas somente em bancas de revista – no formato impresso –, as HQs, hoje, por sua popularização, estão facilmente na internet – em formatos digitais –, supermercados, livrarias, bibliotecas etc. As HQs tornaram-se um meio de comunicação em massa, com ampla variedade de estilos para atrair, atender e cativar seus leitores.
Nos últimos anos, nota-se a presença das HQs no ambiente escolar. Para Vergueiro e Ramos (2019), houve uma gradativa inserção do tema na área educacional brasileira, tanto como atividade de leitura quanto em práticas pedagógicas por meio das inserções desse material nos textos dos Parâmetros Curriculares Nacionais (PCN) (Brasil, 1997; 1998a; 1998b) e no Programa Nacional Biblioteca na Escola (PNBE), transformando os quadrinhos em uma política educacional do país.
Em relação ao ensino de Matemática, ainda hoje, mesmo com diversos recursos tecnológicos, a disciplina ainda é vista como a mais difícil de ser compreendida ou estudada por parte dos alunos. Diante desse cenário, constantemente o ensino da Matemática representa um grande desafio à educação; por esse motivo, o presente trabalho – desenvolvido a partir da dissertação de mestrado “Uma história em quadrinhos para contribuição na produção de significados acerca do Teorema de Pitágoras sob princípios do Modelo dos Campos Semânticos” (Majoni, 2021), sob orientação da Professora Doutora Ligia Arantes Sad – tem como objetivo usar as HQs como recurso didático, de modo que auxilie no desenvolvimento de processos de ensino-aprendizagem na disciplina de Matemática.
Para isso, cria-se a história em quadrinhos "Problemas com o teorema de “Pitágoras”?”, com base no conteúdo matemático Teorema de Pitágoras e aplica-se o material em sala de aula à luz do referencial teórico Modelo dos Campos Semânticos (Lins, 1993).
De modo específico, a pesquisa aconteceu na Escola Estadual de Ensino Fundamental e Médio João Crisóstomo Belesa, localizada em Cariacica, município da zona urbana do Estado do Espírito Santo, durante o período de pandemia da covid-19, em 2021. No total, participaram do estudo 61 alunos (de 160 matriculados) de quatro turmas do 3º ano do Ensino Médio na referida instituição de ensino. No entanto, neste artigo será evidenciado o resultado de uma turma, totalizando 30 alunos.
Com este trabalho, desenvolve-se uma enriquecedora história em quadrinhos para uso em sala de aula, com a possibilidade de produção de significados, visando criar um modo de despertar o interesse dos estudantes ao estudarem Matemática.
Ensino e aprendizagem da Matemática
Quando analisamos os processos de ensino-aprendizagem relativos à Matemática escolar na Educação Básica, é possível observar o desafio encontrado para estudantes e docentes. Paralelo a esse pensamento, D’Ambrosio (1986) ressalta que o ensino da Matemática, na Educação Básica, do ponto de vista da motivação contextualizada, estava se tornando ausente, uma vez que o interesse do estudante é voltado às suas percepções materiais e intelectuais mais imediatas.
É por isso que o ensino da Matemática precisa proporcionar aos estudantes práticas e experiências diversificadas nos processos de ensino-aprendizagem, sendo necessário
contextualizar o conteúdo com a prática vivenciada pelo aluno; mostrar a evolução histórica da Matemática e que ela encontra em permanente evolução, construção; e evidenciar o enredo, ou seja, organizar as ideias matemáticas, conforme elas foram construídas, nas mais diversas áreas de conhecimento (Castejon; Rosa, 2017, p. 15).
Seguindo essa linha de raciocínio, fica evidente então, como observado nos PCN, que “a aprendizagem matemática está ligada à compreensão do significado” e “aprender o significado de um objeto ou acontecimento pressupõe vê-lo em suas relações com outros objetos e acontecimentos” (Brasil, 1997, p. 19).
Por consequência, os processos de produção de significados a respeito da Matemática, para o estudante, resultarão de possíveis conexões que possam vir a ser estabelecidas entre os diferentes temas matemáticos, observando a mudança dos conteúdos da rígida forma de sucessão linear para uma abordagem em que as conexões sejam favorecidas e destacadas.
As HQs podem contribuir nesse sentido, introduzindo um tema, aprofundando um conceito já apresentado. É uma forma de gerar discussão e até mesmo ilustrar uma ideia, trazendo os aspectos históricos das Matemáticas, da evolução das mesmas ao longo dos anos e, assim, possivelmente despertar o interesse do estudante (Majoni, 2021, p. 23).
Como consequência, o ensino não ficará restrito apenas ao desenvolvimento real do estudante, mas também ao processo de interação social e de mediação, como exposto por Vygotsky (1991).
O Modelo dos Campos Semânticos
Em meados de 1992, Romulo Campos Lins buscava relacionar o papel do significado na Matemática. Para o autor, era necessário compreender e caracterizar aquilo que os estudantes pensavam enquanto realizavam atividades de Matemática. Com esse intento, ele desenvolveu o Modelo dos Campos Semânticos (MCS), que tem como bases os processos de produção de conhecimento e de significado.
Para o MCS, na visão de Lins (2012), o conhecimento consiste em uma crença-afirmação em que o sujeito enuncia algo em que acredita. Para tal, é importante que a crença-afirmação ocorra em conjunto com uma justificação, que é aquilo que o sujeito entende como lhe autorizando a dizer o que diz.
Dessa forma, para Lins (1999), as noções tradicionais de conhecimento fazem uma separação entre a proposição (verdadeira) na qual a pessoa acredita e a justificação que a pessoa tem para acreditar naquilo. É por esse motivo que não faz sentido o modelo discutir se uma pessoa tem conhecimento “melhor” do que outra pessoa.
Exemplificando, Sad (1999) afirma que é perfeitamente possível dizer que dois estudantes que estão produzindo significado para a mesma sentença matemática x + 3 = 5 podem constituir conhecimentos diferentes: um por meio da justificação baseada na percepção do estudante de que ao efetuar a soma 2 + 3 ele obterá 5 e outro através da justificação seguindo exemplos do livro didático em que se deve encontrar o valor de x através dos algoritmos de resolução de uma equação do 1º grau.
É importante para o MCS entender o conceito de significado e da sua produção. Como caracterizam Lins e Gimenez (1997, p. 145), “significado é o conjunto de coisas que se diz a respeito de um objeto”, sendo efetivamente o que se diz no interior de uma atividade. No MCS, o aspecto central de toda aprendizagem é a produção de significados. É no interior de um campo semântico que se produz conhecimento e significado, além da constituição de objetos (que estruturam nossa cognição).
Dessa forma, o modelo vê a produção de significados como sendo uma crença, em que há uma afirmação para as coisas que são ditas em determinada atividade, na qual quem está "falando" crê na enunciação, seguindo uma lógica pela qual se faz uma justificação (pode ser também uma fala interna – um falar consigo mesmo – ou por uma linguagem não verbal – sem o uso de palavras). É nessa perspectiva que Silva e Lins (2013) descreve que, se um sujeito produz significados, ele produziu, então, ações enunciativas a respeito de um objeto no interior de uma atividade.
Outra caracterização básica destacada no modelo é o da leitura plausível, muito utilizada nos diálogos e interações em meio aos processos de produção de conhecimento e significado. Para Lins (2012), a leitura plausível indica um processo no qual o todo de que alguém acredita foi dito e faz sentido. Ela é plausível porque “faz sentido” e é aceitável em determinado contexto.
É importante também ressaltar que não quer dizer que toda fala será coerente. Conforme afirma Lins (2012), da mesma forma que há situações nas quais uma pessoa não consiga produzir significado para um resíduo de enunciação, existem também falas para qual essa pessoa não conseguirá produzir coerência plausível.
É por isso que Prata Filho (2018) destaca que, em uma conversa entre professor e estudante, há maior chance de que as leituras plausíveis aconteçam por parte do professor e o entendimento por parte do estudante. O professor deverá escutar, dialogar e ler o estudante – não pelo que ele ainda não conhece, mas pelo que ele enuncia a respeito do objeto que irá se formar ou reinventar.
O presente trabalho enquadra-se nessa linha teórica, uma vez que, além da interação/diálogo entre professor-aluno ou vice-versa, por meio da leitura plausível, a proposta das HQs em sala de aula possibilita a produção de significados.
Local da pesquisa e participantes
A pesquisa de campo aconteceu na Escola Estadual de Ensino Fundamental e Médio João Crisóstomo Belesa, em Cariacica, Estado do Espírito Santo, durante o 2º trimestre (24/05 a 09/09) do ano letivo de 2021.
A instituição encontra-se em região periférica, onde a maioria dos estudantes reside nos bairros próximos à escola tem situação socioeconômica desfavorecida, sendo em sua maioria filhos de pessoas com baixa escolaridade, dentre elas empregadas domésticas, pescadores e trabalhadores da construção civil, como consta do Plano de Desenvolvimento Institucional da escola.
Os participantes desta pesquisa são estudantes de duas turmas do 3º ano do Ensino Médio que foram convidados e, ao aceitar, assinaram o termo de consentimento livre e esclarecido.
Em 2021, durante a pandemia da covid-19, a Secretaria Estadual da Educação, seguindo as normas sanitárias da Secretaria Estadual de Saúde, direcionou o ano letivo para o ensino hibrido. Nesse cenário, os estudantes tinham as seguintes opções para auxiliá-los no processo de ensino-aprendizagem:
- Aulas presenciais, de maneira escalonada (cada turma dividida em 2 grupos), seguindo os protocolos e decretos do Governo do Estado do Espírito Santo;
- Plataforma Google Classroom para o ensino remoto daqueles estudantes que dispõem de meios tecnológicos; e
- Atividades impressas para estudantes que não dispõem de meios tecnológicos.
As aulas presenciais respeitaram um escalonamento (revezamento) diário, com a intenção de contemplar dois grupos de uma mesma turma com o mesmo conteúdo. A carga horária obrigatória dos terceiros anos é de quatro aulas (55 minutos) de Matemática, por turma, durante a semana. Com o escalonamento, foram ministradas presencialmente duas aulas de Matemática por semana para cada grupo.
Do total de 160 alunos matriculados nas duas turmas de 3º ano em que a pesquisa se desenvolveu, 61 alunos participaram do estudo. Apesar de esse número corresponder a 38,36% de participação dos discentes durante todo o período do 2º trimestre, houve grande alternância de frequência por parte dos estudantes e um número expressivo de faltas. Mesmo assim, essa situação não inviabilizou o estudo, uma vez que houve a divulgação dos dias em que as atividades da pesquisa seriam aplicadas.
Para este artigo, optou-se por um recorte dos dados analisados em Majoni (2021), selecionando-se os alunos da turma 1 (3m1, grupo A – 14 alunos – e grupo B – 16 alunos).
A criação das HQs
A HQ "Problemas com o teorema de “Pitágoras”?”, criada por Majoni e Sad (2021), teve como narrativa a vida estudantil do personagem fictício Pedro Henrique, conhecido na história pelo apelido “PH”. O enredo conta a dificuldade de PH na sua escola para estudar Matemática. Com o conteúdo “Teorema de Pitágoras”, a história se desenvolve de modo que PH e seus colegas alcancem o aprendizado dessa matéria e desmistifiquem a dificuldade de aprendizado na disciplina de Matemática.
Em síntese, a confecção desse material aconteceu em três etapas:
- Definição do roteiro, criação dos diálogos, abordagem do conteúdo matemático, divisão dos quadros e esboço das imagens.
- Inserção das falas e criação dos desenhos (manualmente).
- Finalização e digitalização da HQ.
A Figura 1 traz uma página desse material.

Figura 1: Recorte de uma página da HQ
Fonte: Majoni; Sad, 2021, p. 30.
Atividade diagnóstica
Antes de aplicar a HQ em sala de aula e verificar se o material e a abordagem didática auxiliaram nos processos de ensino-aprendizagem de Matemática dos alunos participantes da pesquisa – especificamente no conteúdo “Teorema de Pitágoras” –, os estudantes foram submetidos a uma avaliação de significados e conhecimentos prévios acerca do Teorema de Pitágoras.
O objetivo da atividade ilustrada na Figura 2 é avaliar os conhecimentos produzidos anteriormente pelos estudantes em relação a exercícios e a problemas propostos envolvendo o Teorema de Pitágoras, com formas geométricas e equações, tendo em vista que, de acordo com a BNCC, esse conteúdo também é trabalhado em anos anteriores.

Figura 2: Atividade criada por Majoni para avaliar conhecimentos prévios acerca do Teorema de Pitágoras dos alunos do 3º ano do Ensino Médio
Fonte: Majoni, 2021.
A maioria dos estudantes optou por não responder às três questões. As transcrições a seguir justificam esse resultado. Cabe destacar que, para não haver identificação dos alunos, foram usados apelidos.
Spike: Então não precisa fazer? Porque eu não lembro como faz.
Johnny Blaze: Eu também não lembro!
Peter Quill: Professor, “chega aqui”. Eu não lembro das fórmulas para resolver as que “tem” desenho.
Danny Rand: Eu também não lembro da fórmula, posso deixar em branco?
Shaina: Professor, eu não lembro como se faz...
Para o professor/pesquisador, essa análise foi primordial para identificar alguns limites epistemológicos que criaram um impedimento para que os estudantes produzissem significados em relação às atividades propostas. Vale destacar que, para Lins (1993), esses limites estão relacionados à impossibilidade de um estudante produzir significados para as questões propostas devido à sua forma de operar cognitivamente.
Leitura da HQ
Após a atividade diagnóstica, aconteceu a apresentação da HQ aos estudantes. Essa atividade consistiu na leitura e interpretação da HQ com a finalidade de criar significados para o Teorema de Pitágoras e facilitar o processo de ensino-aprendizagem da Matemática.
É importante ressaltar que a HQ está constituída de uma narrativa que traz em si aspectos da história da Matemática e de situações em que se pode aplicar o Teorema, como, por exemplo, o problema em que é necessário encontrar quantos quilômetros serão asfaltados na estrada que liga as cidades A e C (Figura 3).
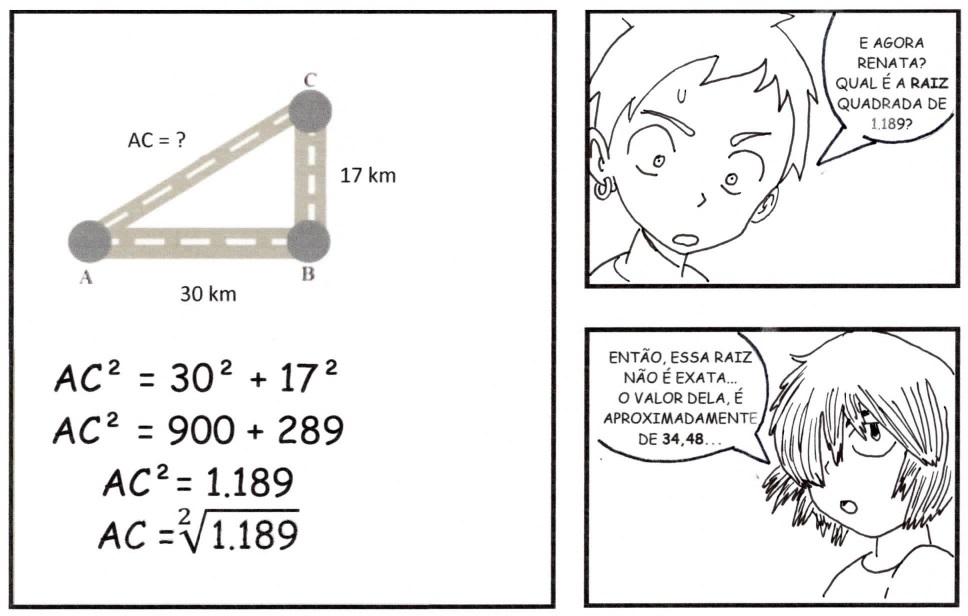
Figura 3: Recorte da HQ aplicada em sala
Fonte: Majoni; Sad, 2021.
Após a leitura da HQ, os estudantes tiveram a oportunidade de descrever suas interpretações sobre pontos chave no processo de produção de significados em relação ao Teorema de Pitágoras e a sua história observadas a seguir.
A estudante Jubilation Lee, em diálogo, destacou que, além de o material ser incrível e apresentar ótima narrativa em conjunto com escrita leve e explicativa, ele contém também exemplos fáceis e rápidos de serem compreendidos. Já Lex Luthor enfatizou que a HQ estava bem estruturada na forma educacional e didática.
Para Freire (1997), esse é um ponto importante de se destacar. Quanto mais o estudante (como leitor da HQ) é desafiado a ser um “re-criador” do texto que ele lê, a compreensão desse texto não se torna estática ou imobilizada nas suas páginas à espera de que o estudante a desoculte, possibilitando, assim, que ele possa ler criticamente a HQ.
Para Daniel, a história é boa para o objetivo da HQ e, apesar de apresentar várias informações em um pequeno espaço de tempo, elas não prejudicam o entendimento. Por outro lado, Sakura alertou para uma quantidade excessiva de informações em alguns quadros, fazendo com que a história se torne “pesada”.
No que tange à história da Matemática descrita na HQ, Spike destacou a evolução do Teorema para a forma que conhecemos hoje. Da mesma maneira, Isaac afirmou que a história do Teorema alinhada com as explicações matemáticas foi um ponto importante.
Sob o ponto de vista motivacional, Jiraya registrou que a ideia de trazer conteúdo matemático para uma HQ com os traços de um mangá pode atrair a atenção de muitos estudantes. Pepper Potts e Lex Luthor destacaram a importância de a HQ retratar um pouco da realidade dos estudantes. Peter Parker consolidou os comentários dizendo que “é uma história para ler com calma. Não muito longa para quem não tem costume de ler, nem muito curta para quem tem esse costume de ler”.
Reúnem-se aqui, feedbacks importantes para a HQ produzida. Todas essas opiniões e críticas constituem, segundo Rama e Vergueiro (2018), elementos merecedores de consideração por parte do professor-pesquisador no que tange às mudanças – textuais, gráficas etc. – necessárias para o aprimoramento da obra.
Além disso, com esses comentários dos estudantes, o professor-pesquisador pôde constatar que é possível, sim, trabalhar Matemática de uma forma mais lúdica, envolvente, de modo que facilite os processos de ensino-aprendizagem e proporcione a produção de significados ao discente, conforme o Modelo dos Campos Semânticos (Lins, 1993).
Considerações finais
Durante a pesquisa, observou-se o quanto é pertinente examinar as HQs sob o ponto de vista de como os seus conteúdos podem ou não interferir de modo positivo no processo de ensino-aprendizagem do estudante. Para isso, deve-se pensá-la de modo que se tenha um projeto político educacional que a torne capaz de intervir socialmente de forma crítica e renovadora e que exerça a criatividade e a imaginação do estudante.
Sendo assim, o presente trabalho, mesmo com as dificuldades do ensino híbrido em virtude da pandemia da covid-19, alcançou seu principal objetivo: utilizar as HQs em sala de aula como material didático, de modo que auxilie no desenvolvimento dos processos de ensino-aprendizagem na disciplina de Matemática.
Os resultados evidenciam que a HQ criada pelo professor-pesquisador é perfeitamente adequada para a sala de aula, uma vez que os alunos demonstraram interesse pela disciplina e pela matéria estudada. Em termos de conclusões, destaca-se que o uso da HQ trouxe uma abordagem do conteúdo matemático do Teorema de Pitágoras, beneficiando a produção de significados e de conhecimentos em ações coletivas e individuais, de modo a subsidiar suas análises e a aprendizagem dos estudantes.
Uma das explicações para o sucesso dessa forma de arte como ferramenta de ensino está no fato de que o leitor pode facilmente estabelecer uma relação com a experiência demonstrada e, assim, mais uma vez, produzir significados, conforme explicita o Modelo dos Campos Semânticos (Lins, 1993).
Por fim, vale destacar que, na dissertação de Majoni (2021), esse tema é mais bem aprofundado e detalhado, sendo aplicadas mais atividades para registro, interpretação e análise dos resultados por parte do professor-pesquisador.
Referências
BRASIL. MEC. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1997. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf. Acesso em: 05 jul. 2020.
______. Parâmetros Curriculares Nacionais: terceiro e quarto ciclos do Ensino Fundamental: Língua Portuguesa. Brasília: MEC/SEF, 1998a. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/portugues.pdf. Acesso em: 05 jul. 2020.
______. Parâmetros Curriculares Nacionais: terceiro e quarto ciclos do Ensino Fundamental: Matemática. Brasília: MEC/SEF, 1998b. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/matematica.pdf. Acesso em: 05 jul. 2020.
CASTEJON, Marângela; ROSA, Rosemar. Olhares sobre o ensino da Matemática: Educação Básica. Uberaba: IFTM, 2017.
D’AMBROSIO, Ubiratan. Da realidade à ação: reflexões sobre educação e Matemática. São Paulo: Summus; Campinas: Editora da Unicamp, 1986.
FREIRE, Paulo. Professora sim, tia não: cartas a quem ousa ensinar. São Paulo: Olho D’Água, 1997.
LINS, Romulo C. Epistemologia, História e Educação Matemática: tornando mais sólidas as bases de pesquisa. Revista de Educação Matemática da SBEM, Campinas, ano 1, nº 1, v. 1, p. 75-91, 1993.
______. Por que discutir teoria do conhecimento é relevante para a Educação Matemática. In: BICUDO, Maria A. V. (org.). Pesquisa em Educação Matemática: concepções & perspectivas. São Paulo: Editora Unesp, 1999. p. 75-94.
______. O Modelo dos Campos Semânticos: estabelecimento e notas de teorizações. In: ANGELO, Claudia Laus et al. (orgs.). Modelo dos Campos Semânticos e Educação Matemática: 20 anos de história. São Paulo: Midiograf, 2012. p. 11-30.
______; GIMENEZ, Joaquin. Perspectivas em Aritmética e Álgebra para o século XXI. 4ª ed. Campinas: Papirus, 1997.
MAJONI, Higor S. Uma história em quadrinhos para contribuição na produção de significados acerca do Teorema de Pitágoras sob princípios do Modelo dos Campos Semânticos. 2021. 179f. Dissertação (Mestrado em Educação em Ciências e Matemática) – Instituto Federal do Espírito Santo, Vitória, 2021.
______; SAD, Lígia A. Problemas com o Teorema de “Pitágoras”?. Vitória: Instituto Federal do Espírito Santo, 2021.
PRATA FILHO, Gilson A. Teorema de Pitágoras a partir da história da Matemática: análises epistemológicas de atividades em turmas do 9º ano da rede pública. 2018. 137f. Dissertação (Mestrado em Educação em Ciências e Matemática) – Instituto Federal do Espírito Santo, Vitória, 2018.
RAMA, Angela; VERGUEIRO, Waldomiro (orgs.). Como usar as histórias em quadrinhos na sala de aula. 4ª ed. 4ª reimpr. São Paulo: Contexto, 2018.
SAD, Lígia A. Cálculo diferencial e integral: uma abordagem epistemológica de alguns aspectos. 1999. 371f. Tese (Doutorado em Educação Matemática) – Universidade Estadual Paulista, Rio Claro, 1999.
SILVA, Amarildo M.; LINS, Romulo C. Sobre a dinâmica da produção de significados para a Matemática. Jornal Internacional de Estudos em Educação Matemática, v. 6(2), p. 1-30, 2013.
VERGUEIRO, Waldomiro; RAMOS, Paulo (orgs.). Quadrinhos na Educação: da rejeição à prática. 2ª reimpr. São Paulo: Contexto, 2019.
VYGOTSKY, Lev S. A formação social da mente. 4ª ed. São Paulo: Martins Fontes, 1991.
Publicado em 25 de outubro de 2022
Como citar este artigo (ABNT)
MAJONI, Higor Soares; SAD, Ligia Arantes. Histórias em Quadrinhos em sala de aula: uma proposta com o Teorema de Pitágoras. Revista Educação Pública, Rio de Janeiro, v. 22, nº 40, 25 de outubro de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/41/historias-em-quadrinhos-em-sala-de-aula-uma-proposta-com-o-teorema-de-pitagoras
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

