Introdução do conceito de número inteiro negativo por meio da noção de subtrações equivalentes: uma proposta de abordagem em turma do 7º ano do Ensino Fundamental
Geisa Abreu Lira Corrêa dos Santos
Mestre em Matemática (PROFMAT/UERJ), professora do Colégio Pedro II
Alexandre Herculano Ferreira Freitas
Doutorando em Ensino e História da Matemática e da Física (UFRJ); professor de Matemática (Prefeitura de São João de Meriti)
Jessica de Oliveira Santiago
Especialista em Metodologias do Ensino da Matemática (UCAM), professora da rede particular em Nilópolis
Ronald Simões de Mattos Pinto
Doutorando em Ensino e História da Matemática e da Física (UFRJ); professor de Matemática do Colégio Pedro II
De acordo com a Base Nacional Comum Curricular (Brasil, 2018), o ensino do objeto matemático número inteiro está previsto para ser concretizado no 7º ano do Ensino Fundamental; é uma das habilidades a serem desenvolvidas pelos alunos, segundo esse documento, a de resolver e elaborar problemas que envolvam operações com esse tipo numérico. No entanto, é bem possível que os alunos da Educação Básica cheguem à sala de aula já tendo empiricamente alguma experiência prévia de mobilização de números inteiros antes mesmo de sua formalização, tendo em vista a presença desse tema em diversas situações cotidianas.
Em particular, no caso do número inteiro negativo, uma dessas situações pode ser evidenciada no contexto esportivo, quando da composição da tabela de pontuação de um campeonato de futebol. Isso se dá especificamente no cálculo do saldo de gols dos times participantes: a subtração que é efetuada entre a quantidade de gols marcados e a de gols sofridos. Os alunos compreendem com não tanta dificuldade que, quando um time sofre mais gols do que marca, a quantidade que expressa esse saldo será representada por um número negativo. Apesar disso, quando da formalização do conceito de número inteiro negativo em sala de aula, é muito comum alunos manifestarem dificuldades em sua compreensão que, em geral, se evidenciam no contexto das operações com números negativos e não da natureza desses números.
Pensando nessas ideias e orientados para a realização de um trabalho para a disciplina de Análise Real, do Programa de Pós-Graduação em Ensino de Matemática da Universidade Federal do Rio de Janeiro, construímos e apresentamos neste artigo uma proposta de abordagem, a ser aplicada em uma turma de 7º ano do Ensino Fundamental, tendo como objetivo o ensino do conceito de número inteiro, em especial, de número inteiro negativo, a partir da noção matemática de subtrações equivalentes. Nossa pretensão é aplicar a proposta numa turma de 7º ano do Ensino Fundamental para coletar e analisar resultados. Contudo, no presente momento vivemos uma emergência sanitária em virtude da pandemia do novo coronavírus, e as escolas se encontram fechadas ou em regime híbrido, com aulas remotas, revezamento de alunos e professores, distanciamento social; essa é uma situação que entendemos inviabilizar, por ora, a aplicação de nossa proposta de abordagem, já que ela culmina num jogo que não teria o mesmo efeito com o distanciamento social.
Organicamente, nossa apresentação está estruturada da seguinte forma: primeiro, estabelecemos uma discussão objetiva teórica sobre esse conceito matemático, a qual subsidiou a construção da abordagem que propomos. Em seguida, destacamos os procedimentos metodológicos empregados no desenvolvimento deste trabalho e caracterizamos a nossa proposta de abordagem. Por fim, tecemos algumas considerações sobre potências e limitações de nossa proposta.
O conceito de número inteiro negativo: algumas objetivas considerações
O conceito de número é um dos mais elementares da Matemática. Historicamente, é possível citar como exemplo das primeiras noções de quantidade por meio de contagem a história dos pastores no controle de seu rebanho, quando se usava como estratégia a comparação entre a quantidade de ovelhas e a de pedras em um saquinho, por meio do que formalmente na Matemática contemporânea conhecemos como estabelecer uma correspondência um a um com um conjunto de referência, ou seja, uma bijeção. Dessa forma, o pastor saberia se o seu rebanho de ovelhas estava completo, se nenhuma ovelha havia se perdido. Esse controle era feito sem precisar atribuir um rótulo que expresse essa contagem concreta, ou seja, antes mesmo de serem desenvolvidos os sistemas de numeração.
Com o passar do tempo e com o aumento das atividades sociais, as diversas civilizações foram estruturando diferentes formas de registrar as contagens e medições, criando rótulos que expressassem a magnitude dessas quantificações. É o que conhecemos como sistemas de numeração – por opção nossa, não discorreremos neste trabalho sobre esses diferentes sistemas.
Atualmente, utilizamos o sistema de numeração decimal indo-arábico. Por meio dele, podemos contar e medir qualquer tipo de coisa, sejam objetos físicos ou conceitos abstratos, tão ínfimos ou tão grandes quanto se queira, usando os mesmos rótulos (números). Por exemplo, em perguntas como: “quantos irmãos você tem?”, “quantos livros temos na mesa?”, mesmo que a resposta possa ser zero, continua sendo o que formalmente classificamos como número natural. Em geral, quando se faz referência a números no dia a dia – emergindo a partir da noção concreta de contagem –, remete-se a esse tipo mais abstrato e elementar de número.
Uma maneira de organizar a discussão sobre a construção do conceito abstrato de número, sob a ótica da Matemática contemporânea, é baseá-la inicialmente em duas noções concretas: contagem e medida, e, a partir delas, compreender como são organizados os diferentes tipos numéricos. Na Figura 1 apresentamos uma representação em diagrama acerca do desenvolvimento do conceito matemático de número partindo dessas duas ideias estruturantes; para efeito deste trabalho, só abordaremos a construção dos números naturais e dos números inteiros.
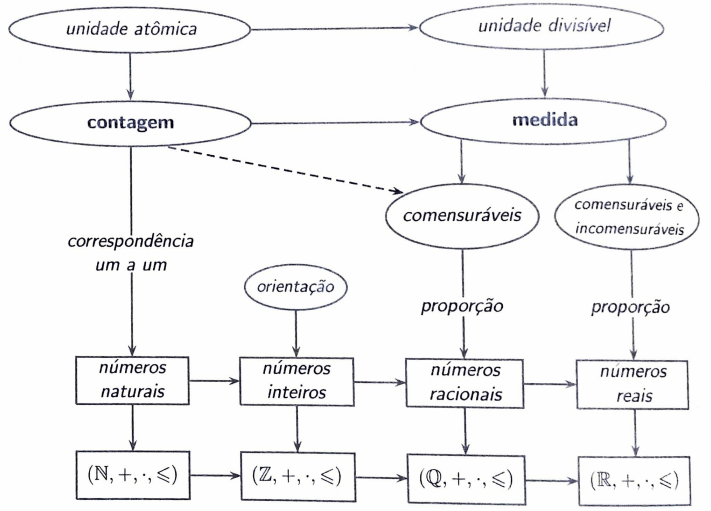
Figura 1: Desenvolvimento do conceito de número
Fonte: Ripoll; Rangel; Giraldo, 2015.
Observando o diagrama, é possível perceber que a noção concreta de contagem, após um passo de abstração (correspondência biunívoca), conduz aos números naturais. Em termos de conjuntos, esse tipo numérico compõe um conjunto cardinalmente infinito que se indica por: ℕ = {0, 1, 2, 3, 4, 5, ...}. Em termos algébricos, esse conjunto é uma estrutura consistente munida de operações e apresentando relação de ordem bem definida (ℕ, +, ∙, ≤).
Nesse sentido, pensando na construção desse conceito pelos alunos da Educação Básica, entendemos ser importante destacar no processo de ensino-aprendizagem que a sequência numérica não é uma simples lista de rótulos a ser memorizada. Ela supõe uma lógica organizacional que formalmente chamamos de composição aditiva. Na prática, cada número é igual ao anterior mais 1: 2 = 1 + 1; 3 = 2 + 1; 4 = 3 + 1 etc.
Além disso, como ampliação, mostra-se que qualquer número pode ser composto por meio da adição entre dois números que o precedem: 8 = 1 + 7 ou 2 + 6 ou 3 + 5 (Nunes et al., 2009).
Retomando o diagrama, percebe-se que a introdução do conceito abstrato de número inteiro se dá a partir da inclusão de mais uma noção concreta: a de orientação. Com efeito, isso representa uma mudança epistemológica importante tanto no próprio sentido elementar de número – o qual deixa de apenas representar uma quantidade (oriunda de uma contagem ou de uma medida) e passa a representar uma quantidade orientada – como também no sentido do zero, que passa a indicar tanto a ausência de quantidade como estar associado a ideia de origem, de referencial dos números positivos e negativos (Ripoll; Rangel; Giraldo, 2015).
Em termos de conjuntos, esse tipo numérico compõe também um conjunto cardinalmente infinito, que se indica por: ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}. Em termos algébricos, esse conjunto é uma estrutura consistente denominada Anel, munida de operações e apresentando uma relação de ordem bem definida (ℤ, + , ∙, ≤). Em sua construção formal, além de estender a estrutura algébrica (ℕ, +, ∙, ≤), o conjunto dos inteiros incorporam outra propriedade importante: a dos inversos aditivos, que dão origem ao que, no ensino na Educação Básica, representamos comumente como números naturais precedidos do sinal de subtração, o conhecido número inteiro negativo.
O conceito de números inteiros é de fundamental dimensão dentro e fora da escola. Durante as aulas, os alunos são colocados frente a situações problema envolvendo números positivos e negativos para representar saldo bancário, aferição de temperatura, medida de altitude, além da tarefa básica de localizar esses números inteiros na reta numérica – nesse caso, por exemplo, dizer qual desses números é o maior: -2 ou -3.
Como até a etapa educacional em que esse conceito é introduzido esses sujeitos só tiveram contato formal com números naturais e com os racionais (nas representações fracionária e decimal), é bastante comum eles sentirem dificuldades quando esse novo tópico é abordado pelo professor. Isso se dá justamente pela necessária ressignificação do conceito de número, passando a entender os números inteiros como uma quantidade munida de orientação, conforme já discutido em linhas anteriores.
Classes de equivalência e a noção de subtrações
Na Matemática contemporânea, uma construção formal do conjunto dos números inteiros é baseada na noção de classe de equivalência. De forma mais precisa, cada número inteiro é “criado” a partir de uma classe de subtrações equivalentes.
Os números inteiros formam um conjunto no qual estão definidas duas operações (que chamamos de adição e multiplicação) e uma relação de ordem que permite comparar seus elementos e que, além disso, é compatível com as operações. Além disso, as operações de soma e produto são articuladas por meio da propriedade distributiva.
Chamamos aqui a atenção para a construção dos números inteiros a partir de uma relação de equivalência definida no conjunto ℕ². Tal procedimento é relativamente comum na Matemática contemporânea. Para isso, vamos introduzir a noção de relação de equivalência.
A relação “é igual a” é um exemplo de relação de equivalência, já que para quaisquer a, b e c temos:
i) a = a
ii) Se a = b então b = a
iii) Se a = b e b = c então a = c.
Dado um conjunto 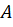 ,
dizemos que
,
dizemos que 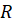 é uma relação de equivalência em
é uma relação de equivalência em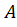 quando as seguintes propriedades são
verificadas, quaisquer que sejam
quando as seguintes propriedades são
verificadas, quaisquer que sejam 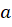 ,
, 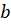 e
e 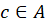 .
.
I. 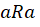 (propriedade
reflexiva)
(propriedade
reflexiva)
II. 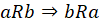 (propriedade simétrica)
(propriedade simétrica)
III. 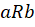 ,
, 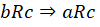 (propriedade
transitiva)
(propriedade
transitiva)
Cada classe de equivalência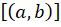 determinada em
determinada em 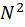 pela relação ~ corresponde a uma classe de subtrações equivalentes, que constitui um número inteiro. Assim,
pela relação ~ corresponde a uma classe de subtrações equivalentes, que constitui um número inteiro. Assim, 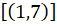 é um número inteiro. O conjunto
é um número inteiro. O conjunto 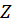 é o conjunto de todas as classes de subtrações
sucessivas. Em símbolos,
é o conjunto de todas as classes de subtrações
sucessivas. Em símbolos, 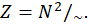
Os pares ordenados 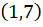 e
e 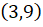 representam uma mesma classe de subtrações equivalentes. A classe pode ser interpretada como um vetor (ou seja, uma classe de segmentos orientados equipolentes) e os pares
representam uma mesma classe de subtrações equivalentes. A classe pode ser interpretada como um vetor (ou seja, uma classe de segmentos orientados equipolentes) e os pares 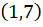 e
e 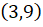 como segmentos orientados que vão, respectivamente, de 7 até 1 e de 9 até 3. Repare que os pares em questão são representantes da classe
como segmentos orientados que vão, respectivamente, de 7 até 1 e de 9 até 3. Repare que os pares em questão são representantes da classe 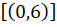 ,
que será, futuramente, associada ao número inteiro com
representação
,
que será, futuramente, associada ao número inteiro com
representação 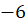 .
.
Além disso, tal definição tem a intenção de identificar os objetos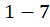 e
e 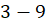 como subtrações equivalentes. Ou seja, tem-se o desejo de identificar ambas as subtrações pelo mesmo objeto matemático. Tal ideia pode ser representada em pares ordenados por
como subtrações equivalentes. Ou seja, tem-se o desejo de identificar ambas as subtrações pelo mesmo objeto matemático. Tal ideia pode ser representada em pares ordenados por 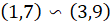 . Note que
. Note que 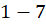 é diferente de
é diferente de 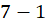 . Assim, o par ordenado é um ambiente natural para demarcar essa diferença. No entanto, não é possível atribuir nenhum significado para os objetos
. Assim, o par ordenado é um ambiente natural para demarcar essa diferença. No entanto, não é possível atribuir nenhum significado para os objetos 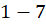 e
e 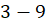 se o nosso ponto de partida são os números naturais e tais representações, evidentemente, não traduzem nenhum significado no domínio dos números naturais. No entanto, se temos a intenção de apresentar tais objetos como equivalentes em algum sentido, podemos nos basear no rascunho
se o nosso ponto de partida são os números naturais e tais representações, evidentemente, não traduzem nenhum significado no domínio dos números naturais. No entanto, se temos a intenção de apresentar tais objetos como equivalentes em algum sentido, podemos nos basear no rascunho 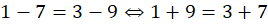 . Note-se que a igualdade do lado direito da equivalência apresentada no rascunho anterior está no campo dos números naturais. Tal igualdade pode ser utilizada como definição para uma relação em
. Note-se que a igualdade do lado direito da equivalência apresentada no rascunho anterior está no campo dos números naturais. Tal igualdade pode ser utilizada como definição para uma relação em 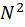 e traduz o desejo de definir subtrações sucessivas. Não é desnecessário comentar, por fim, que a ideia e o rascunho que motivam e dão sentido à definição formalizada muitas vezes são omitidos por diversos autores de livros de Matemática desde a Educação Básica. Tal prática acaba por mitificar os conteúdos matemáticos e podem levar o leitor a pensar
erroneamente que as definições criam as ideias matemáticas.
e traduz o desejo de definir subtrações sucessivas. Não é desnecessário comentar, por fim, que a ideia e o rascunho que motivam e dão sentido à definição formalizada muitas vezes são omitidos por diversos autores de livros de Matemática desde a Educação Básica. Tal prática acaba por mitificar os conteúdos matemáticos e podem levar o leitor a pensar
erroneamente que as definições criam as ideias matemáticas.
A interpretação dos números inteiros por meio de classes de subtrações equivalentes é inspirada na construção formal de 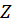 . Não defendemos aqui que os números inteiros sejam definidos dessa maneira na Educação Básica; no entanto, tal formulação serve de inspiração para uma abordagem dos números inteiros na Educação Básica. Queremos aqui afirmar que a Matemática contemporânea não deve chancelar abordagens da Matemática escolar, porém muitas vezes pode servir de inspiração para abordagens na Educação Básica. Ou seja, buscam-se conexões entre duas formas de praticar matemática sem que se produzam hierarquias e de forma que a aproximação seja potente e benéfica para a Matemática
escolar.
. Não defendemos aqui que os números inteiros sejam definidos dessa maneira na Educação Básica; no entanto, tal formulação serve de inspiração para uma abordagem dos números inteiros na Educação Básica. Queremos aqui afirmar que a Matemática contemporânea não deve chancelar abordagens da Matemática escolar, porém muitas vezes pode servir de inspiração para abordagens na Educação Básica. Ou seja, buscam-se conexões entre duas formas de praticar matemática sem que se produzam hierarquias e de forma que a aproximação seja potente e benéfica para a Matemática
escolar.
O método
Primeiramente, definimos em conjunto a temática do trabalho, ou seja, o conceito matemático a ser abordado em nossa proposta: número inteiro negativo. Foram critérios para essa opção tanto a experiência dos autores no ensino desse conceito na Educação Básica como a orientação da disciplina de pós-graduação que estamos cursando, de escolher um assunto matemático que tenha sido abordado nela.
O procedimento metodológico seguinte foi delimitar a etapa da Educação Básica em que pretendemos realizar esse experimento, assim que possível: 7º ano do Ensino Fundamental, por se tratar do momento educacional em que esse conceito é introduzido formalmente para os alunos (conforme destacamos na Introdução).
Em seguida, procedemos a uma revisão bibliográfica (Gil, 2002), ou seja, um mapeamento de livros e artigos científicos que tenham consonância com a temática. Com esse material, construímos uma objetiva, mas consistente, fundamentação teórica que subsidiou a elaboração do trabalho, assim como alumiará nossa análise dos resultados que vislumbramos serem obtidos em uma futura aplicação de nossa proposta de abordagem, a qual será caracterizada mais adiante em função de no presente momento atravessarmos uma situação de pandemia mundial, razão pela qual foram implementadas medidas de fechamento de escolas em alguns lugares e em outros adotou-se um regime híbrido, com aulas remotas, revezamento de alunos e professores dentro das escolas, o que a nosso ver dificulta a aplicação desta proposta de abordagem.
Aqui cabe sinalizar que pensamos em sua aplicação, do ponto de vista metodológico, ser realizada com uma abordagem qualitativa de pesquisa, segundo a qual o investigador não se preocupa em estabelecer quantificações do grupo investigado (Goldenberg, 1999); dá-se mais ênfase ao processo do que ao produto e preocupa-se em retratar a perspectiva dos participantes (Lüdke; André, 2014).
A proposta
O objetivo de nossa proposta de abordagem é a introdução do conceito de número inteiro negativo tendo como recurso teórico a ideia matemática de subtrações equivalentes. Em conformidade com a recomendação da BNCC, sua aplicação se dará em turmas de 7º ano do Ensino Fundamental, e nossa pretensão é que a abordagem seja desenvolvida antes de os alunos conhecerem números negativos – na verdade, como já discutido, é bem possível que eles já conheçam (os que acompanham futebol/esportes, por exemplo – até mesmo crianças do 4° e do 5° anos), só não sabem operar de fato com eles, ou seja, falta a formalização conceitual.
Para começar, veríamos exemplos e casos em que a subtração equivalente é útil e usada com os números naturais. Com o intuito de estimular a investigação por parte dos alunos e a aprendizagem colaborativa, seria proposto a eles que realizassem pesquisas – com pessoas e em meios físicos ou virtuais (livros, sites) – para levantar situações nas quais verificassem a aplicação da noção de subtrações equivalentes e as trouxessem para a sala de aula.
Após discutir sobre essas situações, proporíamos algumas contas a serem resolvidas, como 1000 – 745 e 50 – 31,20; em seguida, analisaríamos as respostas encontradas pelos alunos.
Como forma de destacar a importância da utilização das subtrações equivalentes para facilitar cálculos, inicialmente seria mostrado que, em relação ao primeiro exemplo, em vez de realizar a subtração usual com o procedimento comumente chamado de “pedir emprestado”, quando efetuamos a subtração equivalente 999 – 744 a conta se torna mais simples (até se efetuada mentalmente). Ampliando o entendimento, mostraríamos que essa estratégia também é viável para 998 – 743, 997 – 742 e assim por diante. Mas, quando chegamos à subtração equivalente 994 – 739, seria explicado que não seria conveniente, pois retornaríamos ao problema de “pedir emprestado” do caso inicial. Neste exemplo, as subtrações equivalentes foram geradas diminuindo o valor dos dois termos da operação.
No que se refere ao cálculo da subtração 50 – 31,20, atribuiríamos um significado concreto com a situação cotidiana de resolver problemas em transações comerciais; quando efetuamos uma compra que deu R$ 31,20 e pagamos com uma nota de R$ 50,00 ao funcionário que trabalha no caixa, ele possivelmente pedirá mais R$ 1,20 como forma de facilitar o troco. No caso, vale observar que, para facilitar o troco, a conta é feita “aumentando” os dois números em questão. Em seguida, problematizar com os alunos: há possibilidade de gerar subtrações equivalentes com valores maiores que os originais? Se sim, qual seria uma possível opção? É viável, por exemplo, no caso de o valor pago ser R$ 1.000,00?
Então, após trabalhar com exemplos como esses, cujos resultados das operações estão no campo dos números naturais, e propor atividades em que eles encontrariam qual(is) subtração(ões) equivalente(s) seria(m) mais interessante(s) em cada caso, partiríamos para a proposição de situações envolvendo subtrações entre números naturais em que o resultado é formalmente “desconhecido” para eles.
Uma problematização nesse sentido seria propor que eles façam uma comparação de 10 – 5 = 9 – 4, pensando: será que invertendo a ordem do minuendo e subtraendo em ambos os lados da igualdade a sentença seria falsa, ou seja, os resultados das subtrações deixariam de ser iguais?
Assim, construiremos com os alunos a percepção da ideia de que se 10 – 5 = 9 – 4, então 5 – 10 = 4 – 9, ou seja, o entendimento de que as subtrações 5 – 10 e 4 – 9 representam o mesmo número. Nesse momento, é iniciada a apresentação de um novo objeto que expressa o resultado dessas subtrações equivalentes: o número negativo.
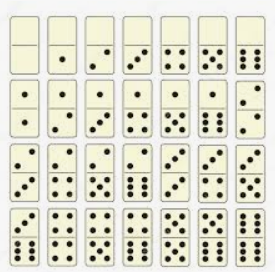
A partir daí, construiríamos de forma colaborativa com os alunos um jogo de dominó ou alguns jogos, dependendo da quantidade de alunos da turma. Seriam formados grupos, e cada grupo construiria o seu dominó. Daí, entraria mais um trabalho de pesquisa, em que eles precisariam entender qual é a configuração de um jogo de dominó: 28 peças, cada uma com duas pontas e 7 números dispostos (0 a 6), como ilustrado na imagem a seguir.
Como se pode ver, o dominó convencional trabalha com números naturais de 0 a 6, dispostos dois deles em cada ponta das peças, repetidos ou não. A ideia é que os alunos criem um jogo de dominó de números negativos, mas, ao invés de a peça conter, por exemplo, os números -2 e - 3, ela conteria diferentes representações para esses números na forma de subtrações equivalentes – nesse caso, respectivamente, poderiam ser as expressões 5 – 7 e 5 – 8.
Na prática, inicialmente cada grupo escolheria os sete números inteiros negativos que comporiam o seu jogo (por exemplo, no Grupo 1 os números poderiam ser -2, -3, - 4, -6, -8, -9 e -10; pela etapa educacional na qual pretendemos aplicar a proposta, pensamos que pedir que escolham números entre -1 e -10 estaria mais adequado à faixa etária e maturidade matemática para a idade/série).
Após escolhidos os sete números, os grupos teriam a tarefa de determinar sete diferentes representações, na forma de subtrações equivalentes, para cada um desses números. Por exemplo: o número inteiro negativo -2 no mesmo jogo poderia estar escrito como 0 – 2, 2 – 4, 3 – 5 etc.
A ideia é o aluno desenvolver a capacidade de identificar que outras representações servem, mesmo que não sejam iguais. Por exemplo, se na mesa temos a peça de dominó que contenha as subtrações 5 – 9 e 4 – 7, seguindo as regras do dominó convencional, o aluno precisa saber que pode usar “o lado” (4 – 7) ligado “ao lado” (5 – 8) de outra peça, conforme exibido a seguir:
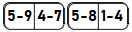
Figura 3: Ilustração de duas peças do dominó de números inteiros.
Por fim, após a construção coletiva dos conjuntos de dominós, partiríamos para a prática do jogo em si, podendo, ao invés de ser jogado de forma individual por quatro alunos como no jogo convencional, ser proposta a composição de quatro duplas de alunos para se ajudarem nos cálculos.
Considerações finais
Este artigo apresentou uma proposta de abordagem do conceito matemático de número inteiro negativo por meio da ideia de subtrações equivalentes. Essa proposta tem o intuito não só de contribuir com uma nova abordagem desse conceito, mas também de fazer o aluno atentar para as diferentes escritas de um número. Desse modo, entendemos que, em etapas escolares posteriores, quando o discente aprender novos operadores matemáticos, ele pode ter a clara compreensão de que 9, 11 – 2, 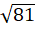 ,
3²,
,
3², 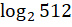 são diferentes representações para o número 9, dependendo do operador matemático que estiver usando.
são diferentes representações para o número 9, dependendo do operador matemático que estiver usando.
Nestas últimas [e não conclusivas] considerações, cumpre-nos registrar que nosso trabalho não tem a pretensão de estabelecer maneiras de ensinar Matemática, ou seja, não se reveste em nenhuma medida de algum caráter idealizador ou prescritivo de ensino.
Podemos elencar duas razões para isso: primeiro, por termos como concepção que não se deve ensinar sem levar em consideração para quem se está ensinando, ou seja, o aspecto político do ato educacional. Afinal, como aponta Freire (1982, p. 97, grifos do autor), “no momento mesmo em que a gente se pergunta em favor de que e contra que, em favor de quem e contra quem eu conheço, nós conhecemos, não há mais como admitir uma educação neutra a serviço da humanidade, como abstração”. É a partir dessa perspectiva que empregamos o termo “proposta”, significando-o como algo não rígido, tendo consciência de que os resultados que podem ser obtidos em diferentes realidades não serão uniformes. Nisso residem as potências e limitações da nossa sugestão de trabalho.
Segundo, porque defendemos a docência como profissão que tem epistemologia própria, cujos saberes são mobilizados, utilizados e produzidos pelos professores no interior de sua prática (Tardif, 2014). Nesse sentido, cada docente, como instância de legitimação de sua própria prática, pode e deve problematizar seus contextos educacionais e fazer os ajustes e aperfeiçoamentos em nossa proposta de abordagem que julgarem necessários.
Por fim, cabe afirmar que vislumbramos em nossa modesta proposta de abordagem, como trabalho de pesquisa e quando de sua possível aplicação, a geração de resultados que poderão contribuir significativamente tanto para a discussão científica sobre a formação inicial de professores que ensinam Matemática como para o processo de ensino-aprendizagem do conceito de número inteiro negativo na Educação Básica.
Referências
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018.
FERREIRA, J. A construção dos números. 2ª ed. Rio de Janeiro: SBM, 2011.
FREIRE, P. Educação: o sonho possível. In: BRANDÃO, C. R. (Org.). O educador: vida e morte. Rio de Janeiro: Graal, 1982. p. 89-101.
GIL, A. C. Como elaborar projetos de pesquisa. 4ª ed. São Paulo: Atlas, 2002.
GOLDENBERG, M. A arte de pesquisar: como fazer pesquisa qualitativa em Ciências Sociais. Rio de Janeiro: Record, 1999.
LÜDKE, M.; ANDRÉ, M. Pesquisa em Educação: abordagens qualitativas. São Paulo: EPU, 2014.
NUNES, T.; CAMPOS, T. M. M.; MAGINA, S.; BRYANT, P. Educação Matemática: números e operações numéricas. 2ª ed. São Paulo: Cortez, 2009.
RIPOLL, C.; RANGEL, L.; GIRALDO, V. Livro do professor de Matemática. Vol. I: números naturais. Rio de Janeiro: SBM, 2015.
RIPOLL, C.; RANGEL, L.; GIRALDO, V. Livro do professor de Matemática. Vol. II: números inteiros. Rio de Janeiro: SBM, 2016.
TARDIF, M. Saberes docentes e formação profissional. Petrópolis: Vozes, 2014.
Publicado em 15 de fevereiro de 2022
Como citar este artigo (ABNT)
SANTOS, Geisa Abreu Lira Corrêa dos; FREITAS, Alexandre Herculano Ferreira; SANTIAGO, Jessica de Oliveira; PINTO, Ronald Simões de Mattos. Introdução do conceito de número inteiro negativo por meio da noção de subtrações equivalentes: uma proposta de abordagem em turma do 7º ano do Ensino Fundamental. Revista Educação Pública, Rio de Janeiro, v. 22, nº 6, 15 de fevereiro de 2022. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/6/introducao-do-conceito-de-numero-inteiro-negativo-por-meio-da-nocao-de-subtracoes-equivalentes-uma-proposta-de-abordagem-em-turma-do-7-ano-do-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.