Sala de aula invertida para o ensino de Matemática no ensino remoto emergencial
Claudia de Oliveira Lozada
Doutora em Educação (USP), docente do Instituto de Matemática da UFAL
Lucas de Morais Carlos
Licenciado em Matemática (IM/UFAL), docente da rede particular de ensino de Maceió
Anneliese de Oliveira Lozada
Doutoranda em Ensino e História das Ciências e da Matemática (UFABC)
A pandemia da covid-19, que se iniciou em 2020, fez com que o sistema educacional brasileiro tomasse novos rumos. Por causa do isolamento social e da suspensão das aulas presenciais, os recursos tecnológicos passaram a ser ferramentas importantes para o processo de ensino-aprendizagem, que passou a ser remoto. Assim, nesse novo contexto as tecnologias digitais de informação e comunicação (TDIC) passaram a ter destaque, mas a recomendação de uso no processo de ensino-aprendizagem já figurava nos Parâmetros Curriculares Nacionais publicados no final da década de 1990, assim como na Base Nacional Comum Curricular publicada em 2018, que inclusive incentiva a promoção da cultura digital em duas de suas competências:
Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva (Brasil, 2018, p. 9).
Por outro lado, esse novo cenário impulsionou também a utilização das metodologias ativas, que, embora não sejam novidade no contexto educacional, não eram adotadas com frequência pelos professores e muitos não conheciam e/ou não dominavam a sua utilização em sala de aula (Alves; Faria, 2020). Por outro lado, pesquisa realizada pela Universidade Federal de Minas Gerais e pela Confederação Nacional dos Trabalhadores em Educação divulgada em 2020 constatou que 89% dos professores não tinham experiência com aulas remotas e 21% afirmaram que é difícil ou muito difícil lidar com tecnologias; o estudo também recomendou que políticas públicas sejam elaboradas para proporcionar cursos de capacitação docente e disponibilização de plataformas educacionais gratuitas (Oliveira, 2020), pois assim fomentam o letramento e a fluência digital.
Assim, muitas escolas, dado o contexto pandêmico, ofertaram, mesmo que muitas vezes de modo mais célere, cursos e palestras para a capacitação dos professores sobre as metodologias ativas (Corral et al., 2021; Ribeiro; Câmara; Silva, 2021). A adaptação dos professores em relação às metodologias ativas teve que ser mais rápida em virtude das necessidades impostas pelo novo cenário educacional, bem como da adaptação dos alunos às aulas remotas e aos novos recursos didáticos tecnológicos.
Bonwell e Eison (1991) citam os pontos positivos da adoção das metodologias ativas no processo de ensino-aprendizagem: os alunos fazem mais do que apenas ouvir (pois desenvolvem a autonomia de estudo com menos dependência do professor e das aulas ministradas na sala de aula, além do hábito de pesquisar), mais ênfase no desenvolvimento de habilidades do que na transmissão de informações, habilidades de ordem superior são direcionadas, maior envolvimento dos alunos nas atividades, ênfase na exploração das atitudes e valores dos alunos (pois as atividades propiciam posicionamento, argumentação e tomada de decisão).
Röj-Lindberg (2001) afirma que a metodologia ativa promove a aprendizagem ativa, que está centrada no aluno, o qual constrói ativamente sua compreensão dos conceitos matemáticos de forma interativa, ou seja, a estrutura e o conteúdo do processo de ensino estão melhorando procedimental e conceitualmente, o que faz com que o conhecimento evolua de modo simultâneo, formando uma rede cognitiva cada vez mais complexa de relações entre diferentes noções matemáticas na mente do aluno. Esse processo ajuda a desencadear o desenvolvimento de habilidades de resolução de problemas e geração de estratégias, segundo a autora, que recomenda ainda que a configuração da sala de aula seja modificada para permitir maior interação entre os alunos durante a aplicação das tarefas matemáticas.
Segundo Röj-Lindberg (2001), a aprendizagem ativa está voltada para o desenvolvimento de competências e da compreensão matemática e deve também mudar a forma com que as discussões matemáticas são iniciadas na sala de aula durante a construção de conhecimento matemático, pois geralmente partem do professor e deve ser dada oportunidade aos alunos de iniciar as interações discursivas, demonstrando as conexões que estabeleceram entre conceitos e procedimentos, indagando os colegas sobre o raciocínio matemático utilizado na resolução das tarefas.
A autora assinala ainda, em relação à aprendizagem ativa da Matemática, que é necessário observar três aspectos: a natureza da tarefa de aprendizagem (de tarefas de Matemática fechadas a tarefas interativas e abertas), a estrutura da sala de aula (de centrada no professor para centrada no aluno, incluindo arranjos adequados do espaço de aprendizagem) e a natureza da interação (desde um tipo de interação unilateral ou bilateral dirigida por um professor até uma interação multilateral entre todos os participantes de um grupo, com base nos requisitos das tarefas de aprendizagem).
Segundo Moran (2014), as metodologias ativas possibilitam maior participação e engajamento dos alunos no processo de aprendizagem. Moran (2018, p. 2) também enfatiza o caráter híbrido das metodologias ativas:
Metodologias ativas são estratégias de ensino centradas na participação efetiva dos estudantes na construção do processo de aprendizagem, de forma flexível, interligada, híbrida. As metodologias ativas, num mundo conectado e digital, se expressam através de modelos de ensino híbridos, com muitas possíveis combinações. A junção de metodologias ativas com modelos flexíveis, híbridos traz contribuições importantes para o desenho de soluções atuais para os aprendizes de hoje.
Além do mais, o novo cenário trouxe à tona aprender de forma autônoma, que pode ser um grande desafio para os alunos, haja vista que, durante todo o seu percurso escolar, desde os anos iniciais do Ensino Fundamental ao Ensino Médio, na maioria dos casos, estão submetidos aos métodos tradicionais de ensino, nos quais não são os protagonistas e sim receptores e reprodutores de conhecimentos. Dessa forma, a autonomia de pensamento e de ação é fundamental na construção do conhecimento, e, segundo Preti (2000, p. 131), a “autonomia significa a capacidade que o sujeito tem de tomar para si sua própria formação, seus objetivos e fins [...], ser autor da própria fala e do próprio agir”. Paiva (2006, p. 88) atrela a autonomia à independência ao afirmar que ela constitui
um sistema sociocognitivo complexo, que se manifesta em diferentes graus de independência e controle sobre o próprio processo de aprendizagem, envolvendo capacidades, habilidades, atitudes, desejos, tomadas de decisão, escolhas, e avaliação tanto como aprendiz de língua quanto como seu usuário, dentro ou fora da sala de aula.
Sendo mais autônomos, menos dependência do professor os alunos terão no processo de aprendizagem. Desse modo, as metodologias ativas constituem uma chave para a mudança de paradigma no que diz respeito a uma nova dinâmica das aulas, revendo o papel do professor no processo de ensino-aprendizagem, em que ele deve atuar como mediador, bem como o papel dos alunos que se tornam protagonistas, participantes ativos e cientes da corresponsabilidade no seu percurso formativo.
Seguindo esse viés, a sala de aula invertida (SAI), também conhecida como flipped classroom, é uma metodologia ativa que possibilita a autonomia e o protagonismo no processo de aprendizagem, uma vez que os alunos têm contato com os conteúdos previamente e de forma diversificada, em vídeos e websites, entre outros, e posteriormente em aula o conteúdo é aprofundado; ou seja, como afirmam Lima e Pavanelo (2017), há um momento de atividades desenvolvidas em sala de aula e outro momento fora dela.
Considerando o que foi discutido como problemática que norteou a experiência a ser relatada neste trabalho, lançamos o seguinte questionamento: quais são as possibilidades e desafios da utilização da sala de aula invertida nas aulas de Matemática do Ensino Médio por meio de ensino remoto?
Com base na problemática e no que foi exposto, este trabalho tem por objetivo apresentar os resultados de uma pesquisa qualitativa sobre a aplicação da metodologia de sala de aula invertida nas aulas de Matemática em uma turma da 1ª série do Ensino Médio de uma escola privada de Maceió/AL, com o ensino remoto emergencial durante o período pandêmico de 2020, verificando suas contribuições para a aprendizagem da Teoria dos Conjuntos.
A sala de aula invertida e a aprendizagem invertida
A metodologia da sala de aula invertida (SAI), segundo Valente (2014), foi proposta em 1996 por Lage, Platt e Treglia em uma aula de Microeconomia na Miami University, em Ohio (EUA), sendo nomeada “inverted classroom”. Os alunos realizavam estudos prévios sobre o conteúdo e nas aulas tinham atividades sobre o que haviam estudado antecipadamente. Com a ascensão do uso das TDIC (tecnologias digitais de informação e comunicação) em sala de aula, houve modernização dos recursos utilizados na sala de aula invertida; assim as instruções passaram a ser online, tendo um percurso marcado pelo aspecto digital.
A sala de aula invertida se baseia na concepção do ensino híbrido, muito utilizado atualmente em virtude das condições geradas pela pandemia da covid-19. No ensino híbrido, a sala de aula invertida “emerge como técnica usada por professores tradicionais para melhorar o engajamento dos estudantes” (Christensen; Horn; Staker, 2013, p. 33).
Valente (2014, p. 86) traz as regras para que se inverta a sala de aula, extraídas do Flipped Classroom Field Guide, publicado em 2014:
1) as atividades em sala de aula envolvem uma quantidade significativa de questionamento, resolução de problemas e de outras atividades de aprendizagem ativa, obrigando o aluno a recuperar, aplicar e ampliar o material aprendido online; 2) Os alunos recebem feedback imediatamente após a realização das atividades presenciais; 3) Os alunos são incentivados a participar das atividades online e das presenciais, sendo que elas são computadas na avaliação formal do aluno, ou seja, valem nota; 4) tanto o material a ser utilizado online quanto os ambientes de aprendizagem em sala de aula são altamente estruturados e bem planejados.
As regras para inverter a aula são essenciais para que o professor compreenda o processo, como a metodologia ocorre e não cometa equívocos em sua aplicação. Schmitz (2016, p. 38) demonstra em um esquema como é a dinâmica da sala de aula invertida, seu processo e as habilidades cognitivas e emocionais que se busca desenvolver com a metodologia.
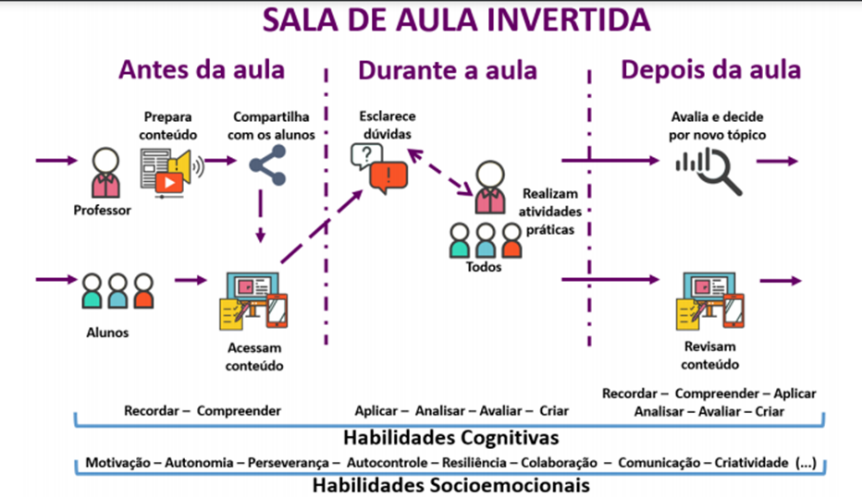
Figura 1: A dinâmica da sala de aula invertida
Fonte: Schmitz (2016).
Nota-se que a sala de aula invertida é uma metodologia que implica planejamento da aula, acompanhamento da aprendizagem e orientação dos alunos, além do feedback. A sala de aula invertida não pode simplesmente se constituir em uma aula semipresencial com tutor, tampouco em atividade de pesquisa realizada fora da sala sem o devido acompanhamento e seguida de seminários e debates na sala de aula feitos sem a mediação adequada.
Aplicações equivocadas da sala de invertida geram efeitos negativos, tais como desmotivação e desinteresse por parte dos alunos na execução da atividade e a percepção de que, na falta de atividades planejadas, optou-se por colocar qualquer atividade para o aluno fazer e obter nota. Portanto, a sala de aula invertida deve ser vista como uma metodologia que possui finalidade de desenvolver habilidades e competências e, como metodologia ativa, deve gerar problematização e reflexão crítica sobre o conteúdo estudado.
Segundo Schneider et al. (2013, p. 71), a sala de aula invertida implica uma reformulação curricular, constituindo
possibilidade de organização curricular diferenciada, que permita ao aluno o papel de sujeito de sua própria aprendizagem, reconhecendo a importância do domínio dos conteúdos para a compreensão ampliada do real e mantendo o papel do professor como mediador entre o conhecimento elaborado e o aluno.
A Flipped Learning Network (FNL) – associação criada nos Estados Unidos para promover a metodologia de sala de aula invertida e que tem como missão fornecer aos professores o conhecimento, as habilidades e recursos para implementar a aprendizagem invertida – publicou seus quatro pilares.
Esses pilares foram escritos por Aaron Sams, Jon Bergmann, Kristin Daniels, Brian Bennett, Helaine W. Marshall, que ajudaram a disseminar a metodologia e integram o conselho da FLN. Primeiramente é preciso compreender que a sala de aula invertida é uma metodologia que pode desencadear a aprendizagem invertida, que é definida assim pelos autores citados:
A aprendizagem invertida é uma abordagem pedagógica em que a instrução direta passa do espaço de aprendizagem em grupo para o espaço de aprendizagem individual, e o espaço de grupo resultante é transformado em um ambiente de aprendizagem dinâmico e interativo, em que o educador orienta os alunos à medida que aplicam conceitos e se envolvem de forma criativa no assunto (SAMS et al., 2014, p. 1, tradução nossa).
Sams et al. (2014, p. 2) afirmam que os pilares da aprendizagem invertida estão ligados ao início da palavra “flipped”, no caso, “flip”: F (flexible environment – ambiente flexível – espaços de aprendizagem escolhidos pelo aluno); L (learning culture – cultura de aprendizagem – aprendizagem centrada no aluno), I (intentional content – conteúdo dirigido – os conteúdos e materiais são escolhidos de modo a proporcionar a compreensão dos conceitos) e P (professional educator – educador profissional – o papel do professor é acompanhar, mediar, dar feedback sobre a aprendizagem e refletir sobre sua própria prática).
Esses pilares estão acompanhados de ações que, em síntese, buscam traçar o processo de aplicação da metodologia de sala de aula invertida, enfatizando principalmente o papel do professor em cada etapa do processo, como podemos ver no quadro a seguir:
Quadro 1: Como proceder na aprendizagem invertida
Pilares da aprendizagem invertida |
Como proceder |
F: Flexible environment – ambiente flexível A aprendizagem invertida permite uma variedade de modos de aprendizagem; os educadores muitas vezes reorganizam fisicamente seus espaços de aprendizagem para acomodar uma lição ou unidade, para apoiar o trabalho de grupo ou estudo independente. Eles criam espaços flexíveis nos quais os alunos escolhem quando e onde aprender. Além disso, os educadores que invertem suas aulas são flexíveis em suas expectativas em relação aos cronogramas dos alunos para a aprendizagem e nas avaliações da aprendizagem dos alunos. |
|
L: Learning culture – cultura de aprendizagem No modelo de aprendizagem invertida, a instrução possui abordagem centrada no aluno, em que o tempo em sala de aula é dedicado a explorar tópicos em maior profundidade, criando ricas oportunidades de aprendizagem. Como resultado, os alunos estão ativamente envolvidos na construção do conhecimento à medida que participam e avaliam sua aprendizagem de maneira que seja pessoalmente significativa. |
|
I: Intentional content – conteúdo dirigido Os educadores de aprendizagem invertida pensam continuamente sobre como podem usar o modelo de aprendizagem invertida para ajudar os alunos a desenvolver conceitos, compreensão, bem como fluência processual. Eles determinam o que precisam ensinar e quais materiais os alunos devem explorar por conta própria. Os educadores usam conteúdo intencional para maximizar o tempo em sala de aula, a fim de adotar estratégias de aprendizagem ativa e centrada no aluno, dependendo do nível de ensino e do conteúdo. |
|
P: Professional educator – educador profissional O papel de um educador profissional é ainda mais importante, e muitas vezes mais exigente em uma sala de aula invertida do que em uma tradicional. No decorrer do tempo de aula, eles continuamente observam seus alunos, proporcionando-lhes feedback relevante no momento de avaliação do seu trabalho. Os educadores profissionais são reflexivos em sua prática, conectam-se uns aos outros para melhorar suas instruções, aceitar críticas construtivas e tolerar “caos controlado” (no sentido de que há uma dinâmica diferente daquela de uma sala de aula tradicional) em suas salas de aula. Enquanto os educadores profissionais assumem papéis menos visivelmente proeminentes em uma sala de aula invertida, eles permanecem como o ingrediente essencial que permite que a flipped learning ocorra. |
|
Fonte: Flipped Learning Network (2016).
Dessa forma, podemos perceber que a aprendizagem invertida e a sala de aula invertida possuem uma estrutura e compreendê-la é fundamental para o planejamento da aula com uma aplicação adequada da metodologia.
Estudos apontam a eficácia do uso da sala de aula invertida nas aulas de Matemática. Katsa, Sergis e Sampson (2016) realizaram uma pesquisa-ação para investigar o impacto da SAI no ensino de Álgebra no Ensino Fundamental e Médio. Os resultados forneceram evidências de melhoria na aprendizagem dos alunos no que diz respeito ao domínio do conteúdo, ao nível de motivação e ao uso do tempo de ensino durante as sessões presenciais na escola.
Cevikbas e Kaiser (2020) apontam que a sala de aula invertida, quando bem planejada e aplicada corretamente, oferece grande oportunidade de promover a compreensão matemática por parte dos alunos, pois os incentiva a se envolver com a aula de Matemática a partir de perspectivas comportamentais, emocionais e cognitivas, além de beneficiar os professores ajudando-os a melhorar suas competências profissionais e transformando a dinâmica da sala de aula, pois aumenta as interações professor-aluno e diminui a indisciplina na sala de aula. Os autores afirmam que, devido à natureza da sala de aula invertida, mesmo que o uso avançado da tecnologia não seja necessário, os professores precisam pelo menos de competências básicas no uso da tecnologia no ensino de Matemática para implantar a sala de aula invertida. Por sua vez, ressaltam que os professores têm papel ativo na SAI e podem fornecer orientação e suporte para os alunos, além de poder acompanhar o progresso do aprendizado dos alunos e oferecer feedback.
Cevikbas e Kaiser (2020) ainda apontam três dificuldades para a implantação da SAI: mudança de paradigma, criação de conteúdo e requisitos técnicos. A dificuldade relativa à mudança de paradigma pedagógico do processo de ensino-aprendizagem de Matemática implica a questão de que crenças e percepções dos alunos e professores podem criar barreiras para a implantação da SAI, como pular as tarefas que são realizadas fora da classe e vir para a sala de aula sem assistir aos vídeos das aulas devido à falta de comprometimento com seu próprio processo de aprendizagem. Daí ser importante a orientação dos alunos em relação à autodisciplina e à responsabilidade no gerenciamento dos seus estudos.
A dificuldade relacionada à criação de conteúdo diz respeito aos recursos necessários para implementar a SAI, como vídeos, slides e outros materiais de ensino que precisam ser bem preparados, pois em geral há certa dificuldade para encontrar vídeos personalizados que atendam efetivamente às necessidades dos alunos e do próprio professor. Os autores afirmam que, embora haja vídeos acessíveis em plataformas como YouTube e Khan Academy, muitos não cobrem ou não correspondem a todos os conteúdos que serão ensinados na aula de Matemática, e os professores precisam criar seus próprios vídeos, o que pode ser uma tarefa demorada. A dificuldade relacionada aos requisitos técnicos diz respeito ao acesso à internet e aos dispositivos móveis, sendo necessário que haja boa conexão e equipamentos, porque os autores enfatizam que a prática de sala de aula invertida não funciona bem sem a internet. Além dessas dificuldades, Cevikbas e Kaiser (2020) explicam que podem existir outras, tais como insatisfação em relação à metodologia, falta de disposição dos alunos para resolver as atividades propostas e preconceito contra a SAI.
Também é importante salientar que a SAI, embora tenha caráter flexível que estimula a autonomia dos alunos, não opera de modo que os alunos tenham menos orientação e suporte na aprendizagem dos conteúdos; pelo contrário, demanda assistência e feedback para que os alunos evoluam das habilidades primárias de compreender e aplicar para as habilidades superiores de analisar, sintetizar, avaliar e criar, que exigem um pensamento e raciocínio mais complexos, como explica Cramer (2015).
Passemos ao relato de experiência com o uso da sala de aula invertida.
Metodologia, resultados e discussões
Este trabalho é um estudo qualitativo (Ludke; André, 1986) a respeito da metodologia de sala de aula invertida; para tanto, aplicamos a metodologia numa turma da 1ª série do Ensino Médio de uma escola privada de Maceió com a finalidade de verificar a aprendizagem do conteúdo de Teoria dos Conjuntos. A turma era composta por quinze alunos que estavam em ensino 100% remoto em 2020. A metodologia foi aplicada para os quinze alunos em ensino remoto, dividindo-os em três grupos com cinco componentes cada.
Para o desenvolvimento da atividade, tomamos como base as competências previstas na BNCC (Brasil, 2018) e elaboramos um quadro com as habilidades a serem desenvolvidas e que se relacionam com o conteúdo de Teoria dos Conjuntos.
Quadro 2: Competências e habilidades
Atividade – sala de aula invertida Componente curricular – Matemática / 1ª série do Ensino Médio Conteúdo: Teoria dos Conjuntos |
|
Competência geral - BNCC (Brasil, 2018, p. 9-10)
|
|
Competências específicas segundo a BNCC (Brasil, 2018, p. 531) |
Habilidades relativas ao conteúdo de Teoria dos Conjuntos (Aspectos conceitual, procedimental e atitudinal), adaptado de Chavante e Prestes (2016, p. 310) |
|
|
Em virtude da adoção de aulas remotas em decorrência da pandemia, as práticas pedagógicas da escola sofreram mudanças significativas para se adaptar ao novo contexto, ampliando a utilização de tecnologias digitais de informação e comunicação (TDIC) para promover maior participação dos alunos nas atividades propostas. Aliás, a BNCC (Brasil, 2018), seguindo o direcionamento de documentos curriculares anteriores, incentiva a utilização das TDIC nas aulas e promove a cultura digital em uma de suas competências gerais:
Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva; compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva (Brasil, 2018, p. 9).
A escola onde foi aplicada a SAI possui um sistema de ensino com plataforma digital com interface organizada pedagogicamente, com atividades variadas e que permitem verificar o desenvolvimento dos alunos considerando a matriz de competências e habilidades da BNCC (Brasil, 2018); mesmo antes da pandemia já havia adotado a prática de metodologias ativas variadas nas aulas. Uma das metodologias ativas adotada nas aulas de Matemática remotas durante a pandemia foi a sala de aula invertida.
Foram feitas adaptações no processo da sala de invertida, uma vez que as aulas presenciais foram suspensas e passaram a acontecer pela plataforma de webconferência da escola. A turma foi dividida em três grupos e foram solicitados os seguintes tópicos do conteúdo da Teoria dos Conjuntos: união de conjuntos, interseção de conjuntos e diferença de conjuntos. Na elaboração das videoaulas, foi solicitado que os alunos apresentassem a parte conceitual e procedimental do conteúdo de Teoria dos Conjuntos e resolvessem exercícios, questões de vestibulares e situações-problema, mostrando também as aplicações do conteúdo no cotidiano e curiosidades.
O planejamento da sala de aula invertida consistiu em dividi-la em quatro momentos:
- Compartilhamento do conteúdo sobre Teoria dos Conjuntos no ambiente virtual de aprendizagem da escola para que os alunos pudessem acessar;
- Esclarecimento de dúvidas dos alunos em uma aula por meio da plataforma de webconferência;
- Atividade prática: gravação de videoaulas pelos alunos sobre o conteúdo de Teoria dos Conjuntos; e
- Apresentação das videoaulas em uma aula na plataforma de webconferência, discussão do conteúdo, revisão e feedback.
Passemos a uma descrição das aulas gravadas pelos alunos e as análises. O Grupo I procurou fazer uma revisão sobre o conteúdo de Teoria dos Conjuntos apresentando os conceitos básicos, como representação dos conjuntos, relação entre elementos e conjuntos e tipos de conjuntos, colocando em seguida uma questão e resolvendo-a passo a passo. Os conceitos foram apresentados por meio de textos escritos manualmente; o grupo procurou destacar com canetas coloridas os pontos principais do conteúdo, como se pode notar no print da imagem do vídeo. Em relação aos aspectos didáticos empregados pelo grupo, a explicação do conteúdo e resolução da questão estavam bem claras e objetivas, o que não ensejava dúvidas.

Figura 2: Videoaula gravada pelo Grupo I
Fonte: Acervo dos autores, 2020.
O Grupo II focou a videoaula em resolução de situação-problema, com ênfase na fixação dos conceitos de interseção e diferença entre conjuntos. O grupo procurou explorar a representação gráfica e as perguntas postas pela situação-problema, explicando o processo de resolução para se chegar à resposta de cada uma. Foram bastante objetivos na explicação.

Figura 3: Videoaula gravada pelo Grupo II
Fonte: Acervo dos autores, 2020.
O Grupo III também focou na resolução de situação-problema relacionada ao cotidiano, e a representação gráfica foi utilizada para expor a resolução que envolvia interseção e união de conjuntos. Também apresentou uma explicação clara e objetiva, com o passo a passo da resolução e justificando as quantidades distribuídas nos conjuntos.
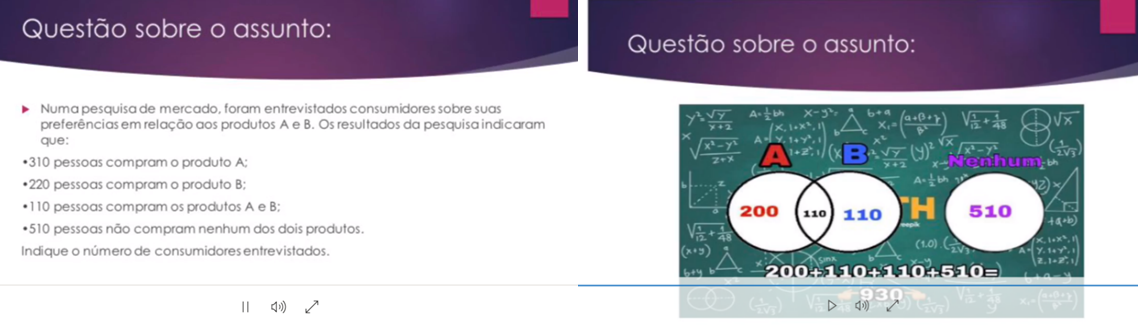
Figura 4: Videoaula gravada pelo Grupo III
Fonte: Acervo dos autores, 2020.
Após a apresentação, as videoaulas ficaram disponibilizadas na plataforma de ensino da escola para que todos os alunos do Ensino Médio tivessem acesso ao conteúdo.
Durante o acompanhamento da atividade, notou-se a colaboração dos alunos no momento do esclarecimento de dúvidas, pois, além de explanarem suas dúvidas, também fizeram afirmações pertinentes emitindo opiniões e sugestões a respeito de como podiam organizar os conteúdos que seriam abordados na videoaula.
A recepção dos alunos à metodologia de sala de aula invertida foi positiva; os alunos tiveram desempenho excelente na dinâmica proposta, acessando o conteúdo, esclarecendo as dúvidas, participando das discussões e, sobretudo, na gravação das videoaulas, seja na seleção e organização do conteúdo, seja na edição dos vídeos. Após a finalização da atividade, ao reuni-los na plataforma de webconferência para o feedback, eles afirmaram que a atividade os motivou, despertou mais o hábito de pesquisa e que tiveram que aprender a delegar tarefas e ter autogerenciamento para cumpri-las.
O acompanhamento e a mediação nas diferentes etapas da metodologia pelo professor constituíram um aspecto importante para o êxito na aplicação da metodologia. Como avaliação, foi adotada a abordagem formativa para olhar o processo como um todo e o desenvolvimento dos alunos ao longo das etapas, assim como uma avaliação somativa individual, visto que é uma exigência da escola. Cruzando as duas abordagens, foi possível aferir notas aos alunos e assim considerar o aspecto qualitativo do processo.
Por outro lado, alguns alunos externaram dificuldades em explicar os processos de resolução das situações-problema em virtude de timidez, mas mesmo assim realizaram a gravação das videoaulas, e esse aspecto constituiu um desafio positivo para eles desenvolverem habilidades socioemocionais como comunicação, criatividade e perseverança, entre outras.
Além do mais, os alunos mobilizaram habilidades cognitivas de recordar, compreender, analisar e avaliar, importantes nos processos matemáticos, e conseguiram assimilar o conteúdo de Teoria dos Conjuntos. A resolução das situações-problema também levou à redução no nível de dificuldade na resolução de questões de vestibulares e do Enem, em que em geral eles apresentavam maior dificuldade quando eram propostas nas aulas. A seguir, apresentamos um quadro com as possibilidades e os desafios observados na aplicação da metodologia de sala de aula invertida na aula de Matemática com base na experiência relatada.
Quadro 3: Possibilidades e desafios do uso da sala de aula invertida
Possibilidades |
Desafios |
Solicitar vídeos e materiais para trabalhar determinado conteúdo. |
Alguns alunos são adeptos dos métodos tradicionais; assim, devemos prestar atenção nos alunos que não estão conseguindo assimilar a metodologia de sala de aula invertida porque o que é para ser benéfico pode se transformar em algo traumático e desmotivador. |
Realizar apresentação prévia dos conteúdos antes de solicitar alguma atividade; isso motivará os alunos e será um guia. |
Alguns alunos podem falar que não sabem ou não conseguiram entender o conteúdo de forma autônoma; assim, é importante uma apresentação prévia do conteúdo. |
Solicitar resoluções de questões de vestibulares, questões contextualizadas e que representem aplicações dos conteúdos matemáticos no cotidiano. |
O vestibular é um dos focos do ensino privado; dessa forma, é necessário acrescentar no planejamento do uso da metodologia questões do Enem e de vestibulares. |
Deixar os grupos livres para realizar as atividades da forma que achar melhor, o que auxilia no desenvolvimento da autonomia. |
Deixar os alunos livres é essencial, porém eles podem procrastinar e a metodologia se tornar desmotivadora; por isso, o professor deve fazer o acompanhamento do processo. |
Disponibilizar os resultados da aplicação da metodologia para os professores de outras disciplinas, pois isso pode motivá-los a também adotar alguma metodologia ativa em suas aulas. |
Muitos professores adotam o método tradicional de ensino; porém, como o ambiente escolar é completamente diversificado, é interessante também a diversificação de métodos de ensino nas salas de aula. |
É importante o professor observar os desafios que enfrentará com a aplicação da metodologia de SAI porque implica desconstruir a forma como se vê a sala de aula tradicional, as interações com os alunos e o modo como os conteúdos matemáticos são trabalhados. Também é imprescindível que se conscientize de que a metodologia de sala de aula invertida é uma ferramenta de ensino-aprendizagem e que pode não ter receptividade por todos aos alunos, cabendo ao professor realizar a inserção daqueles que apresentem certa resistência ou que não se adaptem à metodologia. Ademais, ao longo da aplicação da metodologia, deve-se refletir sobre como a dinâmica da sala de aula invertida está acontecendo, os avanços, percalços e redirecionamentos que deverá tomar, considerando como pontos a se aperfeiçoar em sua aplicação numa próxima aplicação da metodologia.
Considerações finais
Como vimos neste trabalho, a metodologia de sala de aula invertida pode ser eficaz quando for devidamente planejada, sua aplicação tenha acompanhamento e a mediação seja feita de forma correta pelo professor, não devendo ser uma atividade “coringa” a ser utilizada em momentos específicos em que não houve planejamento da aula.
Aspectos como desenvolvimento de habilidades socioemocionais – autonomia, colaboração, comunicação, criatividade, resiliência e perseverança – são importantes para que os alunos não desistam de realizar as atividades propostas, uma vez que sua execução depende de eles se organizarem, se disciplinarem e monitorarem a si mesmos, assumindo o protagonismo e a responsabilidade pelo processo de aprendizagem.
Por outro lado, quando aplicada corretamente, a metodologia contribui para o desenvolvimento de habilidades e competências e inserção de novas práticas de ensino nas aulas de Matemática, com mudança de paradigmas, essencial para o que o processo de ensino-aprendizagem seja inovador e estimule os alunos a uma participação mais ativa nas aulas.
Consideramos que a aplicação da metodologia de sala de aula invertida relatada aqui, ofertada para o ensino remoto emergencial em pleno período pandêmico, mostrou-se eficaz, criando um ambiente de ensino-aprendizagem interativo e flexível, possibilitando que os alunos fomentassem a própria construção do conhecimento na interação social e na colaboração (Cevikbas; Kaiser, 2020), ressaltando que demandou a realização da mediação de modo assertivo para que os alunos pudessem realizar as atividades e os objetivos fossem atingidos. Além disso, as possibilidades e desafios observados foram elencados no sentido de trazer reflexões para melhorar as práticas futuras em ensino remoto.
Constatou-se que houve assimilação do conteúdo de Teoria dos Conjuntos e os exemplos explanados nas videoaulas foram importantes nesse processo, havendo apropriação conceitual, procedimental e atitudinal do conteúdo, na medida em que puderam visualizar suas aplicações por meio das situações-problema que os alunos apresentaram.
Por fim, a experiência contribuiu significativamente para que os estudantes desenvolvessem autonomia e vivenciassem uma nova forma de interação durante o processo de aprendizagem; ela foi realizada inteiramente por meio digital e exigiu a coordenação entre eles e os tempos e espaços, que passaram a ser diferentes daqueles das aulas presenciais, bem como possibilitou ao professor ter uma visão macro do processo de ensino-aprendizagem e da importância de gerenciá-lo, acompanhando suas etapas, fazendo as intervenções necessárias, auxiliando os alunos em relação às dúvidas que surgiam, sem lhes tirar a autonomia e o protagonismo durante a aplicação da metodologia na construção do conhecimento matemático.
Referências
ALVES, E. J.; FARIA, D. C. Educação em tempos de pandemia: lições compreendidas e compartilhadas. Revista Observatório, v. 6, nº 2, p. 1-18, 2020.
BONWELL, C. C.; EISON, J. A. Active learning: creating excitement in the classroom. Washington: The George Washington University/School of Education and Human Development, 1991.
BRASIL. Base Nacional Comum Curricular.Brasília: MEC/Secretaria de Educação Básica, 2018.
CEVIKBAS, M.; KAISER, G. Flipped classroom as a reform-oriented approach to teaching mathematics. ZDM Mathematics Education, nº 52, p.1.291-1.305, 2020.
CHAVANTE, E.; PRESTES, D. Quadrante Matemática – 1º ano: Ensino Médio. São Paulo: Edições SM, 2016.
CHRISTENSEN, C. M.; HORN, M. B.; STAKER, H. Ensino híbrido:uma inovação disruptiva? Uma introdução à teoria dos híbridos. São Paulo: Clayton Christensen Institute, 2013.
CORRAL, A. C. T.; RIBEIRO, L. A.; QUELUCI, G. C.; HANDEM, P. C. (Re)Aprendendo novas formas de ensinar: ações de extensão adaptadas para aprendizagem durante a pandemia de covid-19. Raízes e Rumos, v. 9, nº 1, p. 131-142, 2021.
CRAMER, Z. Active learning and flipped classrooms in introductory math. 2015. Disponível em: https://www.math.uwaterloo.ca/~zcramer/Z.%20Cramer%20-%20Active%20Learning%20and%20Flipped%20Classrooms%20in%20Intro%20Math.pdf. Acesso em: 08 ago. 2021.
FLIP LEARNING. What is flipped learning? 2016. Disponível em: https://flippedlearning.org/wp-content/uploads/2016/07/FLIP_handout_FNL_Web.pdf. Acesso em: 05 mar. 2021.
KATSA, M.; SERGIS, S.; SAMPSON, D. G. Investigating the potential of the flipped classroom model in k-12 mathematics teaching and learning. 2016. Disponível em: https://files.eric.ed.gov/fulltext/ED571429.pdf. Acesso em: 08 ago. 2021.
LUDKE, M.; ANDRÉ, M. E. D. A. Pesquisa em educação: abordagens qualitativas. São Paulo: EPU, 1986.
MORAN, J. A educação que desejamos: novos desafios e como chegar lá. Campinas: Papirus, 2014.
______. Metodologias ativas e modelos híbridos na educação. 2018. Disponível em: http://www2.eca.usp.br/moran/wp-content/uploads/2018/03/Metodologias_Ativas.pdf. Acesso em: 04 mar. 2020.
OLIVEIRA, E. Quase 90% dos professores não tinham experiência com aulas remotas antes da pandemia; 42% seguem sem treinamento, aponta pesquisa. O Globo, 8 de julho de 2020. Disponível em: https://g1.globo.com/educacao/noticia/2020/07/08/quase-90percent-dos-professores-nao-tinham-experiencia-com-aulas-remotas-antes-da-pandemia-42percent-seguem-sem-treinamento-aponta-pesquisa.ghtml. Acesso em: 22 abr. 2022.
PAIVA, V. L. M. Autonomia e complexidade. Linguagem & Ensino, Pelotas, v. 9, nº 1, p. 77-127, 2006.
PAVANELO, E.; LIMA, R. Sala de aula invertida: a análise de uma experiência na disciplina de Cálculo I. Bolema, Rio Claro, v. 31, p. 739-759, ago. 2017.
PORTAL FLIPPED CLASSROOM. Flipped Classroom Field Guide. 2014. Disponível em: https://docs.google.com/document/d/1arP1QAkSyVcxKYXgTJWCrJf02NdephTVGQltsw-S1fQ/pub#id.suagqb7wve21. Acesso em: 05 mar. 2021.
PRETI, O. (Org.). Educação a distância: construindo significados. Cuiabá: Nead/IE-UFMT; Brasília: Plano, 2000.
RIBEIRO, A. F. P.; CÂMARA, J. F. P.; SILVA, N. N. C. Capacitação online dos docentes durante a pandemia. Revista Interdisciplinar Parcerias Digitais, v. 5, p. 1-10, 2021.
RÖJ-LINDBERG, A. S. Active learning of mathematics. 2001. Disponível em: http://www.vasa.abo.fi/users/aroj/Active%20learning%20of%20mathematics.pdf. Acesso em: 10 abr. 2021.
SAMS, A. et al. Definition of flipped learning. 2014. Disponível em: https://flippedlearning.org/definition-of-flipped-learning/. Acesso em: 10 abr. 2021.
SCHMITZ, E. X. S. Sala de aula invertida: uma abordagem para combinar metodologias ativas e engajar alunos no processo de ensino-aprendizagem. 2016. Disponível em: https://nte.ufsm.br/images/PDF_Capacitacao/2016/RECURSO_EDUCACIONAL/Material_Didatico_Instrucional_Sala_de_Aula_Invertida.pdf. Acesso em: 02 mar. 2021.
SCHNEIDER, E. I. et al. Sala de aula invertida em EaD: uma proposta de blended learning. Intersaberes, v. 8, p. 68-81, 2013.
VALENTE, J. A. Blended learning e as mudanças no Ensino Superior: a proposta da sala de aula invertida. Educar em Revista, Curitiba, nº 4, p. 79-97, 2014.
Publicado em 10 de janeiro de 2023
Como citar este artigo (ABNT)
LOZADA, Claudia de Oliveira; CARLOS, Lucas de Morais; LOZADA, Anneliese de Oliveira. Sala de aula invertida para o ensino de Matemática no ensino remoto emergencial. Revista Educação Pública, Rio de Janeiro, v. 23, nº 1, 10 de janeiro de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/22/47/sala-de-aula-invertida-para-o-ensino-de-matematica-no-ensino-remoto-emergencial
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

