Um diálogo entre a construção de conceitos de Matemática e Física
Vitor Acioly
Doutor em Ensino de Física (UFRJ), professor do Instituto de Física da UFF
Estudantes entusiasmados com a Física comumente tratam a Matemática como se fosse uma reles ferramenta para quantificar os resultados das teorias elaboradas nesse ramo de pesquisa. Por outro lado, alguns estudantes entusiasmados com a Matemática consideram a Física como mais um ramo de estudo da Matemática ou simplesmente Matemática Aplicada. Essas visões preconceituosas são resultado da falta de compreensão da Matemática (ou da Física) pelos entusiastas da Física (ou da Matemática).
No presente texto serão apresentadas algumas relações entre a Física e uma importante disciplina da Matemática denominada Análise Real. O nome Análise Real refere-se ao estudo dos elementos do conjunto dos números reais (ℝ) e as funções definidas a partir de subconjuntos do conjunto dos números reais cujas imagens também são formadas por números reais.
Essa disciplina, em muitos cursos de Matemática, é apresentada na aula inicial como a formalização da disciplina Cálculo Diferencial e Integral. Esta última, por sua vez, tem como uma de suas origens o texto do notório Isaac Newton intitulado Principia – Princípios Matemáticos de Filosofia Natural, que utilizou ferramentas básicas da Matemática.


Figura 1: Capas dos livros da Edusp que contêm a tradução em língua portuguesa da obra Principia – Princípios Matemáticos de Filosofia Natural, de Isaac Newton, publicada originalmente em 1687
Além de ser uma das origens do Cálculo Diferencial e Integral e por sua vez a Análise Real, a obra de Isaac Newton utilizou ferramentas básicas da Matemática, especialmente da Geometria, como os postulados contidos na obra histórica Os elementos, de Euclides, para fundamentar a Mecânica Clássica, com suas leis para o movimento de corpos, a Lei da Gravitação Universal, e demonstrar as leis de Johannes Kepler (1571-1630), matemático e astrônomo alemão para o movimento dos planetas, que haviam sido obtidas empiricamente.
De certa forma, o trabalho de Newton permitiu expandir a Geometria (euclidiana), que pode ser interpretada como um ramo da Matemática palpável na realidade para estudar os demais fenômenos da natureza, ou seja, a Física. Após o trabalho de Newton, a Análise Real (e o Cálculo Diferencial e Integral) adquiriu consistência teórica e relevância dentro do campo da Matemática e até notação própria para os seus operadores: limite, derivada e integral, entre outros, devido a trabalhos de outros renomados matemáticos. Sim, Isaac Newton foi um matemático!
A disciplina Análise Real e algumas de suas aplicações na Física
A disciplina Análise Real comumente é apresentada nos cursos de graduação e pós-graduação dividida em alguns tópicos: Teoria de Conjuntos e Funções; Conjuntos Finitos, Enumeráveis e Não Enumeráveis e a Estrutura Algébrica dos Conjuntos Numéricos (ℕ, ℤ e ℚ); Os Números Reais (ℝ); Sequências e Séries; Construção dos Conjuntos Numéricos (ℕ, ℤ, ℚ, ℝ e ℂ); Topologia da Reta, Limite e Continuidade de uma Função; Derivada de uma Função; Integral de Riemann de uma Função; Sequência de Funções.
Nesta seção serão feitas algumas correlações entre tópicos da disciplina Análise Real e o estudo da Física clássica e moderna. Os tópicos não citados como correlatos de fenômenos físicos de forma direta em grande maioria contribuem na fundamentação da Análise Real e, portanto, atuam indiretamente na formalização matemática dos fenômenos físicos.
Teoria de Conjuntos e funções
O uso de funções na Física é algo natural devido à necessidade do entendimento do comportamento dos fenômenos e no auxílio à previsão do que determinado fenômeno acarretará no futuro. Um exemplo bem simples são as funções horárias da posição (
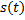 ) e da velocidade (
) e da velocidade (
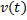 ) de uma partícula em movimento retilíneo e variado, dados por e, respectivamente, para t ≥ 0, onde
) de uma partícula em movimento retilíneo e variado, dados por e, respectivamente, para t ≥ 0, onde
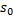 é posição inicial,
é posição inicial,
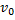 é a velocidade inicial, a é a aceleração constante e t é a variável tempo.
é a velocidade inicial, a é a aceleração constante e t é a variável tempo.
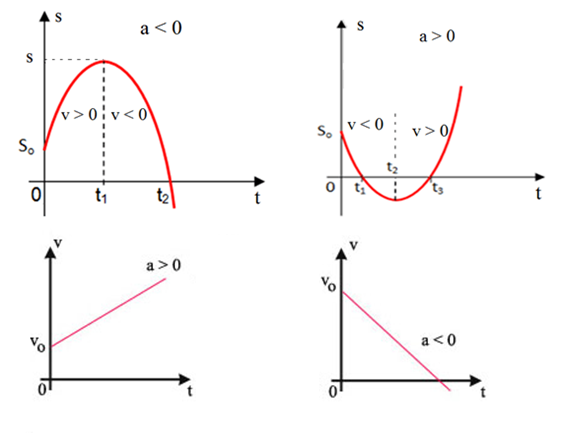
Figura 2: Na parte superior, comportamento da posição; na inferior, o comportamento da velocidade: à esquerda para movimento acelerado (a > 0) e à direita para movimento retardado (a < 0)
Conjuntos finitos, enumeráveis e não-enumeráveis e a estrutura algébrica dos conjuntos numéricos (ℕ, ℤ e ℚ)
Apesar da impressão de que a natureza se comporta como meio contínuo na Física moderna, podemos observar alguns problemas que, devido às condições de contorno, possuem um conjunto enumerável de soluções, podendo esses conjuntos ter quantidade finita de elementos ou não. Dessas soluções derivou o termo quântico por se tratar de conjuntos de solução em que é possível contar seus elementos. Um caso notório é devido à equação diferencial de Schrödinger, que, na sua forma unidimensional independente do tempo é por
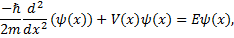
onde é a função de onda independente do tempo em função da coordenada x, é a constante de Planck h dividida por 2π, m é a massa da partícula, é a função energia potencial e E é a energia do sistema. Um interessante exemplo é o caso de uma partícula presa em um poço de potencial quadrado infinito. Nesse exemplo, a partícula se move livremente no interior do intervalo [0, L]; a função energia potencial é dada por:
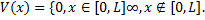
As funções de onda que satisfazem a equação de Schrödinger nessas condições são da forma:
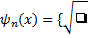
E os valores possíveis de energia E são dados por:
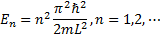

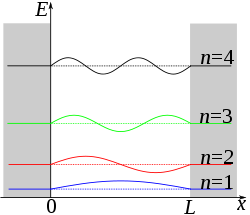
Figura 3: À esquerda, esquema do poço de potencial quadrado infinito; à direita, os possíveis níveis de energia e suas respectivas funções de onda
Esse exemplo ocorre com as partículas denominadas quarks,que são completamente confinadas no interior dos nêutrons e prótons devido a uma propriedade dos prótons e nêutrons chamada liberdade assintótica.
Um exemplo mais conhecido é o que considera a função energia potencial oriunda da lei de Coulomb, que dá a origem de um modelo de um poço de potencial, também infinito, para tratar, por exemplo, a atração entre os elétrons e o núcleo do átomo. Nesse exemplo utiliza-se a equação de Schrödinger independente do tempo na sua forma tridimensional e em coordenadas polares. Em coordenadas polares, a função energia potencial é dada por:
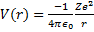 ,
,
onde é a constante de Coulomb, Ze é a carga do núcleo do átomo, -e é a carga do elétron e r é a distância entre o elétron e o núcleo. Nesse caso, as possíveis energias do sistema, considerando a massa do elétron denotada por, são dadas por:
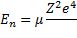
para algum inteiro positivo l. Nessa aplicação, cada En representa uma camada eletrônica da órbita do átomo.
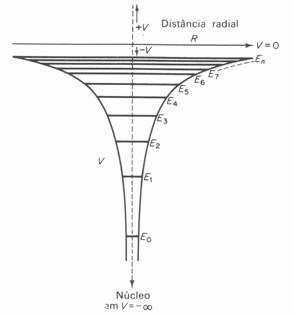
Figura 4: Potencial coulombiano V(r) e seus autovalores En
Topologia da Reta
De forma sintética, a Topologia da Reta tem como objetivo criar uma classificação para os subconjuntos do conjunto dos números reais; eles podem ser conjuntos ditos abertos, conjuntos fechados, conjuntos não abertos nem fechados, conjuntos densos, conjuntos de interior vazio, conjuntos compactos. Além disso, na Topologia da Reta são estudadas as operações entre esses conjuntos citados, como interseção e união. Com o passar do tempo, a topologia foi generalizada para além do conjunto dos números reais, em especial para conjuntos de dimensões maiores que 1.
Newton, ao descobrir e formalizar a Lei da Gravitação Universal, estudou os efeitos da gravidade na natureza, dizendo que “dois corpos atraem-se com força proporcional às suas massas e inversamente proporcional ao quadrado da distância que separa seus centros de gravidade”. Contudo, Albert Einstein, com a Teoria da Relatividade Geral, procurou o que causa a força gravitacional.
E a resposta encontrada por Einstein e outros pesquisadores, como Karl Schwarzschild, foi que a massa dos objetos deforma o espaço-tempo, alterando a sua topologia.
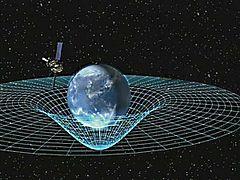
Figura 5: Ilustração da deformação que o espaço-tempo sofre devido à massa do planeta Terra
Enquanto Einstein resolveu as equações da Teoria da Relatividade Geral por meio de uma série de aproximações, o astrônomo alemão Karl Schwarzschild, enquanto estava no front russo da Primeira Grande Guerra, leu o trabalho de Einstein e obteve uma solução exata para esse sistema de equações ao supor que a massa de uma estrela estática e simétrica esfericamente estava concentrada em um único ponto, um ponto de singularidade. Além disso, Schwarzschild determinou um raio em torno desse ponto de singularidade que forma uma esfera fechada, uma região compacta do espaço, na qual toda forma de matéria ou mesmo a luz que a toca não conseguem retornar. A fronteira dessa esfera recebe o nome de horizonte de eventos; esse raio é dado por:
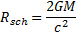
onde é o raio de Schwarzschild, G é a constante gravitacional, M é a massa do corpo celeste e c é a velocidade da luz no vácuo.
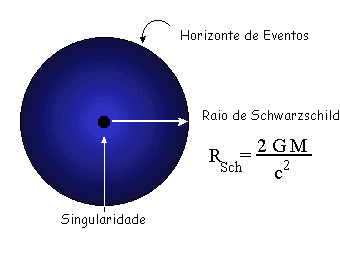
Figura 6: À esquerda, ilustração esquemática do ponto de singularidade do raio de Schwarzschild e o horizonte de eventos. À direita, ilustração mostrando a deformação no espaço-tempo causada pelo Sol, por uma anã branca, estrela de nêutrons e por um buraco negro
A partir do raio de Schwarzschild, é possível definir o buraco negro como sendo um objeto cujo raio é menor do que seu raio de Schwarzschild. O buraco negro é literalmente um buraco no espaço-tempo. Como o buraco negro pode ser concebido como uma esfera fechada, qualquer região do espaço-tempo é relativamente aberta, assim como o subconjunto [0,2]-{1} é relativamente aberto em relação ao seu fecho, o intervalo real [0,2]. O horizonte de eventos é a fronteira dessa esfera, e nela o tempo simplesmente para, o que justifica fisicamente o buraco no espaço-tempo.
Limite e continuidade de uma função
O conceito de limite e continuidade é aplicado de forma ampla em toda a Física clássica. Isso é devido à hipótese de tratar a matéria como um fluido ou sólido ou como um meio contínuo. Dizer que determinado corpo está sob a hipótese de meio contínuo é equivalente a dizer que a variação de suas propriedades materiais é tão suave que o Cálculo Diferencial (ou seja, a Análise Real) pode ser usado em sua análise.
A principal propriedade medida sob a hipótese de meio contínuo é a massa específica ρ (ou densidade), que é bem definida como:
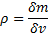
Essa situação é ilustrada na figura a seguir, na qual a “massa específica” calculada por meio da massa molecular dentro de um dado volume é plotada em gráfico em função do tamanho da unidade de volume. Há um volume limite abaixo do qual as variações moleculares podem ser importantes e acima do qual as variações de agregações podem ser importantes.
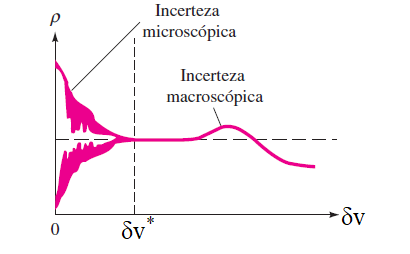
Figura 7: Massa específica calculada em função do tamanho do volume elementar
Para gases e líquidos à pressão atmosférica, por exemplo, a ordem de grandeza de é de 1 nano de milímetro cúbico (10-9mm3). A maioria dos problemas de Engenharia e de Física clássica trabalha com dimensões físicas muito maiores do que esse volume limite, de maneira que a massa específica é essencialmente uma função pontual e as propriedades dos materiais podem ser consideradas variando continuamente no espaço.
Derivada e integral de uma função
Os primeiros exemplos de derivada e integral que a maioria dos estudantes vê no Ensino Fundamental e Médio são vistos na Física. Para a derivada, temos a velocidade instantânea dada por meio do seguinte limite:
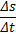
onde  é a variação de deslocamento e
é a variação de deslocamento e  é a variação de tempo. Para a integral, é o cálculo da área abaixo do gráfico da curva de velocidade para determinar o deslocamento que determinado objeto móvel sofreu. Com o tempo, a ciência evoluiu, forçando as derivadas e as integrais a também evoluírem, resultando nas derivadas de ordem superior, derivadas parciais, derivadas materiais, integrais múltiplas, de linha e de superfície. Elas são necessárias para modelar diversos fenômenos físicos, gerando equações integro-diferenciais como, por exemplo, a equação da continuidade:
é a variação de tempo. Para a integral, é o cálculo da área abaixo do gráfico da curva de velocidade para determinar o deslocamento que determinado objeto móvel sofreu. Com o tempo, a ciência evoluiu, forçando as derivadas e as integrais a também evoluírem, resultando nas derivadas de ordem superior, derivadas parciais, derivadas materiais, integrais múltiplas, de linha e de superfície. Elas são necessárias para modelar diversos fenômenos físicos, gerando equações integro-diferenciais como, por exemplo, a equação da continuidade:
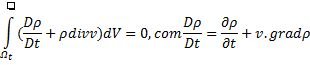
e da quantidade de movimento linear
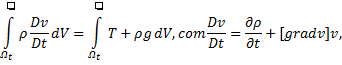
em suas formas globais. Suas formas locais são obtidas considerando a região tão pequena quanto se queira, e são dadas respectivamente por:
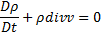
e
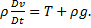 ,
,
onde 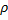 é a massa específica, v é o vetor velocidade, g é o vetor aceleração da gravidade e T é o tensor tensão dependente das propriedades do material estudado. Dessas equações, por exemplo, advêm as conhecidas equações de Navier-Stokes da Mecânica dos Fluidos.
é a massa específica, v é o vetor velocidade, g é o vetor aceleração da gravidade e T é o tensor tensão dependente das propriedades do material estudado. Dessas equações, por exemplo, advêm as conhecidas equações de Navier-Stokes da Mecânica dos Fluidos.
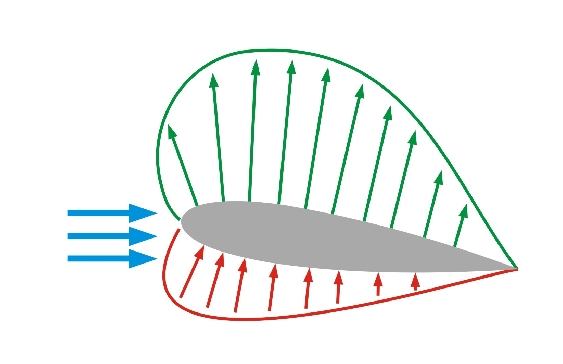
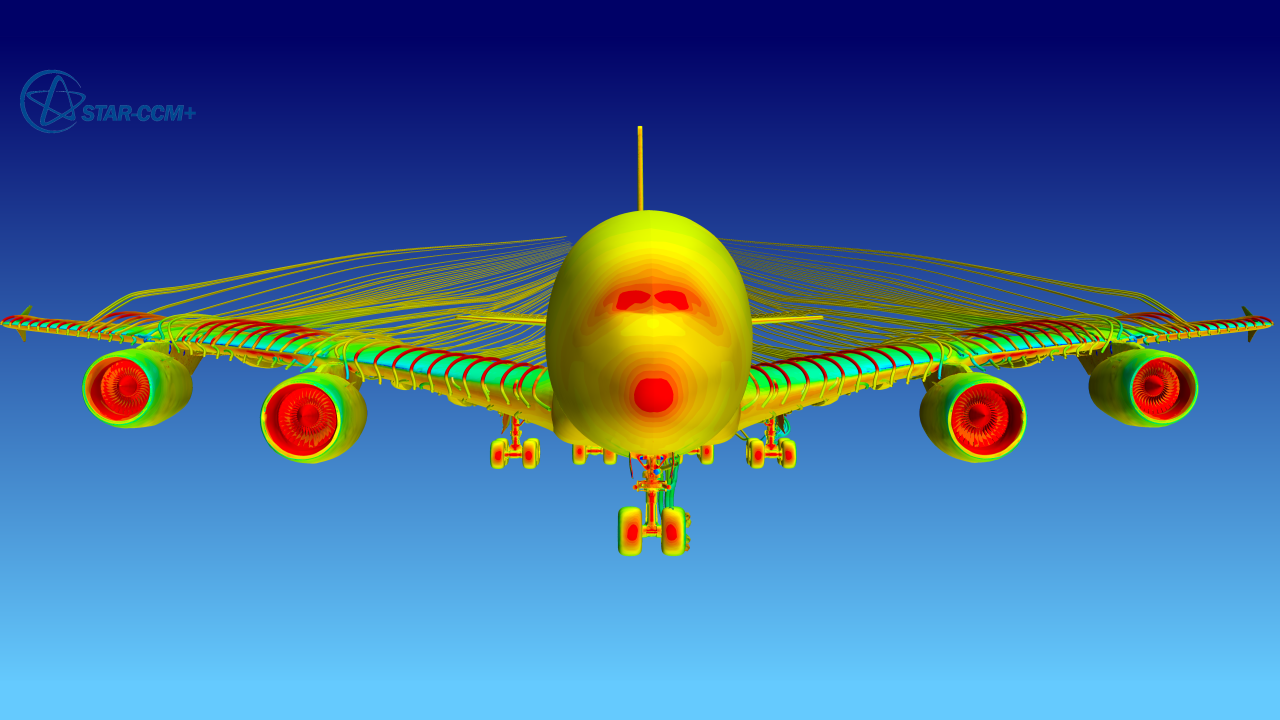
Figura 8: Exemplo de aplicação da Mecânica dos Fluidos na Engenharia Aeronáutica para o cálculo de tensões atuantes sobre a asa de um avião
Sequência de funções
Levar o conceito de sequência e série de números para o conjunto das funções de variável real resultou em um importante instrumento para a ciência, em especial o conjunto das funções definidas em um intervalo limitado e fechado, no qual é fácil introduzir uma norma por meio da integral definida. Uma das principais aplicações de sequências e séries de funções é na resolução de equações diferenciais, pois, se existem duas soluções para uma equação diferencial, a soma delas também será solução da equação.
Nesse âmbito, uma das principais é a série de Fourier, que foi desenvolvida pelo matemático e físico francês Jean Baptiste Joseph Fourier durante o seu estudo sobre propagação de calor. A série de Fourier de uma função 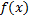 é dada por:
é dada por:
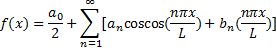
com
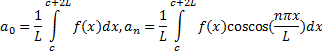
e
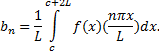
A série de Fourier possui diversas aplicações na Física, como na já mencionada propagação de calor, na Acústica, na Mecânica dos Fluidos, na Eletrostática e na Eletrodinâmica.
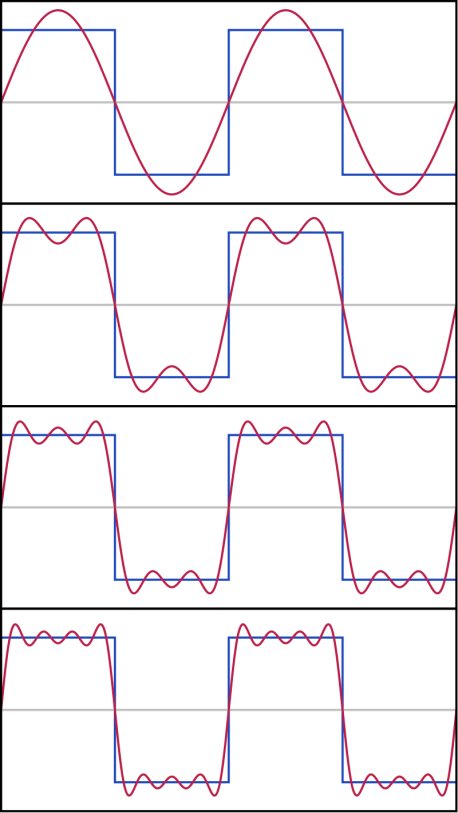
Figura 9: As primeiras quatro somas da série de Fourier de uma onda quadrada. A onda quadrada é encontrada frequentemente nas áreas da Eletrônica e do processamento de sinais
Conclusões
É fato que Albert Einstein, quando jovem, não tinha muito apreço pela Matemática, como ele mesmo diz: “Meu interesse pelo estudo da natureza era, sem dúvida, maior. E, quando eu era estudante, ainda não estava convencido de que o conhecimento aprofundado dos princípios básicos da Física dependesse de métodos matemáticos sofisticados”. Mas, com a sabedoria obtida com os anos, ele reconheceu a importância da Matemática para fundamentar e abrir novos caminhos na Física, e a Análise Real (e o Cálculo Diferencial e Integral) cumpriu papel essencial nesse processo.
Referências
EISBERG, R.; RESNICK, R. Física Quântica. Rio de Janeiro: Elsevier, 1979.
GURTIN, M. E. An introduction to continuum mechanics. v. 158. New York: Academic Press, 1981. (Mathematics in Science and Engineering).
KAPLAN, I. Física Nuclear. 2ª ed. Rio de Janeiro: Guanabara Dois, 1978.
LIMA, E. L. Curso de Análise. 11ª ed. Rio de Janeiro: Associação Instituto de Matemática Pura e Aplicada, 2004.
NERI, C.; CABRAL, M. Curso de Análise Real. 2ª ed. Rio de Janeiro: Instituto de Matemática/UFRJ, 2009.
RIPOLL, C.; RANGEL, L.; GIRALDO, V. Livro do Professor de Matemática na Educação Básica: números inteiros. vol. II. 2ª ed. Rio de Janeiro: SBM, 2016.
WHITE, F. M. Mecânica dos Fluidos. 6ª ed. Porto Alegre: McGraw-Hill, 2011.
Publicado em 17 de janeiro de 2023
Como citar este artigo (ABNT)
ACIOLY, Vitor. Um diálogo entre a construção de conceitos de Matemática e Física. Revista Educação Pública, Rio de Janeiro, v. 23, nº 2, 17 de janeiro de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/1/um-dialogo-entre-a-construcao-de-conceitos-de-matematica-e-fisica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

