Contribuições para a aprendizagem da Matemática na Educação Básica
Jorge Luiz Alves de Souza
Licenciado em Pedagogia (UENF)
Eliane Vigneron Barreto Aguiar
Doutora em Informática na Educação (UFRGS), Cederj (UENF)
Este artigo apresenta algumas das possíveis causas das dificuldades do aluno na aprendizagem da Matemática na Educação Básica. Segundo Sousa e Silva (2016), muitos alunos demonstram deficiências na aprendizagem provenientes de uma má formação oriunda, em sua maioria, do processo de ensino-aprendizagem. Isso vai se acumulando nas séries seguintes, produzindo cada vez mais dificuldades no aprendizado, desestimulando, provocando insegurança e interferindo no lado emocional da criança, tornando-os desmotivados ao aprendizado da Matemática.
Fiorentini (2008) comenta a respeito da relevância do aperfeiçoamento do professor em sua formação profissional no intuito de proporcionar um ensino motivador ao aluno, visto que o professor é desafiado incessantemente a buscar maneiras diferentes de ensinar. Com o surgimento das novas tecnologias, o processo de ensino exige do professor uma maior habilidade para utilizar recursos didáticos diversificados e tecnológicos e não somente o livro e o quadro escolar.
No entendimento dos autores Gasperi e Pacheco (2018), a Matemática pode ser trabalhada de forma contextualizada, conforme sua história na evolução da humanidade. Nesse contexto é fundamental a intermediação do professor, mostrando a aplicabilidade da Matemática no dia a dia das pessoas.
Pensando em uma educação de qualidade, os Parâmetros Curriculares Nacionais (PCN) (Brasil, 1997) vieram para ser uma referência para educação em todo o Brasil, pois permitem uma flexibilização do currículo, de acordo com as regiões, para estimular a qualidade do ensino.
Para os PCN (Brasil, 1997), os professores de Matemática devem trabalhar em sala de aula prioritariamente com recursos didáticos, como jogos, livros, vídeos, computadores e tablets. O objetivo é que a criança aprenda e não decore, por isso o professor deve utilizar os recursos disponíveis para trabalhar com problemas que mostrem a realidade, facilitando a compreensão.
De acordo com o Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira, (INEP), o Brasil participou do Programa de Avaliação Internacional de Estudantes (PISA), desde a sua primeira edição, em 2000; é uma avaliação desenvolvida e coordenada pela Organização para Cooperação e Desenvolvimento Econômico (OCDE). Ela acontece a cada três anos, realizando um estudo comparativo entre os países participantes e buscando informações sobre o sistema educacional. Em 2018, a Matemática foi avaliada de acordo com a “capacidade de formular, empregar e interpretar”, com o objetivo de verificar as habilidades e os conhecimentos adquiridos ao longo da Educação Básica dos estudantes na faixa dos 15 anos aos 16 anos e 2 meses. Participaram 79 países, com um total aproximado de 600 mil alunos, sendo 10.691 estudantes de 597 escolas brasileiras (Brasil, 2020).
O PISA 2018 mostrou que “68,1% dos estudantes brasileiros não possuem nível básico de Matemática”. Além disso, fazendo uma comparação com os demais países da América do Sul, o Brasil ficou nas últimas posições no ranking, entre o 69º e o 72º. Mais de 40% desses jovens não conseguiram resolver questões simples de Matemática e apenas 0,1% dos 10.691 alunos participantes alcançaram o nível máximo (Brasil, 2020).
Diante do exposto, o artigo identifica algumas das principais dificuldades dos estudantes no aprendizado da Matemática na Educação Básica. Além disso, apresenta os possíveis recursos didáticos que podem minimizar essas dificuldades.
Dificuldades na aprendizagem da Matemática
Há séculos, a Matemática é ensinada. Percebe-se que é preciso encontrar uma maneira de fazer com que os alunos aprendam a disciplina de modo significativo. Brossi (2021), ao tratar do início da vida escolar, afirma que quando o aluno chega à escola para iniciar sua vida educacional, ele traz consigo o que aprendeu com a família e com amigos. Isso mostra que o aluno carrega uma bagagem com muitas informações e, sem dúvida, com diferenças entre eles. Portanto, cabe ao professor perceber essas diferenças e corrigir os erros que os alunos trazem de suas experiências pessoais, a fim de que não impeçam o seu desenvolvimento.
Sousa (2015) afirma que se nos anos iniciais escolares a criança não consegue se desenvolver em Matemática, nos anos seguintes ela pode apresentar ainda mais dificuldades com a disciplina. Além disso, a criança pode ficar desestimulada ao aprendizado. Isso provoca uma baixa autoestima, acarretando prováveis problemas futuros no desenvolvimento da aprendizagem matemática.
Ao falar sobre conhecimentos prévios, Vasconcelos (2000) diz que sem esses conhecimentos não se pode partir para as matérias mais complexas. Essa deficiência impossibilita que o aluno se desenvolva adequadamente, visto que não apresenta os requisitos necessários para os anos subsequentes.
Menez e Lima (2021) descrevem diversas dificuldades que os alunos apresentam em conteúdos matemáticos básicos, como a não compreensão da simbologia e das relações matemáticas, a não interpretação dos problemas e, também, a não compreensão de conceitos básicos matemáticos, demonstrando a falta de conhecimentos anteriores, o que dificulta no andamento da série seguinte.
Segundo Piaget (1973), quando o conhecimento acontece, há uma consolidação das estruturas do pensamento. Segundo as fases do desenvolvimento, a criança vai montando suas estruturas de pensamento, ou seja, a parte biológica é fundamental para o desenvolvimento cognitivo da criança. Com isso, na fase chamada por Piaget de operatório formal (a partir dos doze anos), a criança se torna capaz de trabalhar com questões lógicas abstratas, bem como criar situações hipotéticas.
Para Vygotsky (2008), “o desenvolvimento humano e intelectual das crianças ocorre em função das interações sociais e condições de vida”. Quando uma criança se relaciona e interage com o outro (meio, pessoa), acontece uma internalização dessas interações, levando o sujeito ao desenvolvimento cognitivo. Portanto, a interação da criança com o outro (que tem mais conhecimento), a estimula à aprendizagem. Isso ocorre de “fora para dentro”.
De acordo com a zona de desenvolvimento proximal (ZDP), a criança com algum conhecimento se relaciona com outra criança ou com o professor. Nesse processo, ela está aprendendo algo novo e chegando ao seu potencial. A ZDP é relevante para a aprendizagem da criança, porque representa um espaço entre o que a criança sabe fazer sozinha (seu conhecimento consolidado) e o que a criança poderá fazer somente após a interação com o meio ou com outra pessoa com maior conhecimento que ela (conhecimento ainda não consolidado) (Vygotsky, 2008).
Para Leung (2001) e Ma (2010), a formação do professor é fundamental para que o aluno cresça dentro de uma perspectiva diferente. Assim, evidencia-se a importância do professor em manter-se sempre atualizado, atento aos recursos didáticos manipuláveis disponíveis para melhorar a compreensão dos alunos no processo de aprendizagem.
Silva (2015) e Brossi (2021) comentam que, com o passar do tempo, tudo vai sofrendo alterações, e a educação não foge disso. A maneira de trabalhar em sala de aula e de abordar os conceitos da disciplina também passam por mudanças. Podem surgir dificuldades de aprendizagem que poderão ser minimizadas se o professor estiver sempre aberto às mudanças e às atualizações no âmbito escolar.
Considera-se relevante, também, trabalhar o raciocínio lógico do aluno para que ele consiga resolver os problemas em Matemática, bem como entender o que se pede numa determinada atividade. A criatividade deve ser estimulada pelo professor em sala de aula, porque além de provocar a curiosidade dos alunos levando-os a pensar, permite, também, que organizem seu pensamento lógico, olhando para os problemas de forma mais criteriosa (Bernardi; Cordenonsi; Scolari, 2007).
Materiais didáticos para aprender a Matemática
Para Gellert (2004), Rodrigues e Gazire (2012), o material didático é tudo aquilo que pode auxiliar o professor a trabalhar com os alunos para que melhorem seu aprendizado, devendo ser intencional e aplicado pelo professor. O material didático pode apresentar maneiras diferentes de concepção do conhecimento, bem como formas distintas de assimilar o aprendizado.
A Base Nacional Comum Curricular (BNCC) (Brasil, 2018, p. 276), documento normativo, orienta que existem alguns materiais que ajudam na compreensão da Matemática, por exemplo, a malha quadriculada, os ábacos, os jogos, os livros, os vídeos e determinados programas de computador. Esses materiais citados são recursos didáticos para o ensino da Matemática em sala de aula e, quando trabalhados integralmente, com criatividade, podem fazer com que os alunos reflitam durante o processo de aprendizagem.
Silva e Benigno (2012) e Silva (2015), afirmam que os jogos e os materiais manipuláveis podem ser aliados auxiliares do professor na intenção de ter um melhor resultado. Cada atividade deve ser preparada para dar apoio ao aprendizado de forma agradável, despertando a curiosidade e a criatividade dos alunos. Nessa fase da vida, as brincadeiras e os jogos fazem parte das atividades dos alunos. A aula não deve estar atrelada somente ao resultado, mas às ações dos alunos e suas experiências.
Exemplos de materiais didáticos
Considerando as ideias de Rodrigues e Gazire (2012) do professor como facilitador da aprendizagem em sala de aula, apresentamos materiais para que o docente desenvolva ações dentro de uma proposta de atividade aplicada. Essa manipulação visa um melhor entendimento e desempenho da capacidade de concentração, de reflexão e de resolução de problemas do seu aluno. Alguns recursos para aprender a Matemática nos anos iniciais da Educação Básica, tais como, o material dourado, o ábaco, os softwares educativos e o uso de material didático reciclado (e suas aplicações) são mostrados a seguir.
Material dourado
A Figura 1 mostra o material dourado, recurso muito utilizado nas escolas para trabalhar os conceitos de unidades, dezenas e centenas e, também, as operações matemáticas. Segundo Rodrigues (2012), esse método foi criado pela italiana Maria Montessori e tem o objetivo de fazer com que o aluno consiga sair do concreto para o abstrato.
Conforme apresentado na Figura 1, esse sistema de numeração decimal é muito trabalhado para que os alunos possam entender a troca de unidades para dezena, de dezena para centena e de centena para milhar. Juntando dez cubinhos pode-se fazer a troca por uma barra, dez barras por uma placa e dez placas por um cubo. Esse material possibilita uma melhor visualização das operações matemáticas.
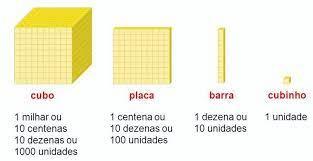
Figura 1: Material dourado
Fonte: Pinterest, 2021.
Para Marques e Simião (2011), o material dourado facilita o aprendizado da soma, da subtração, da multiplicação e da divisão, pois com a utilização das peças o aluno percebe o valor, quantifica e entende melhor o processo das trocas nas operações.
Ábaco
O ábaco é uma das máquinas de cálculo mais antigas criadas pelo homem, que possibilita transitar pelas unidades, dezenas e centenas com mais clareza na observação do resultado. Além disso, apresenta um material colorido e agradável de ser manipulado (Oliveira, 2019).
A Figura 2 mostra um ábaco de pino onde o aluno pode trabalhar as operações. Da direita para a esquerda, os pinos representam as ordens das unidades, dezenas, centenas, unidade de milhar, dezena de milhar e centena de milhar. Cada pino recebe no máximo nove unidades, chegando a nove passa para o outro pino onde se faz a troca. No ábaco de pino ainda é possível efetuar as operações de soma, subtração, entre outros cálculos (Silva, 2022).
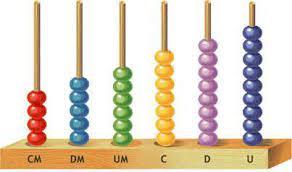
Figura 2: Ábaco
Fonte: Educador, 2021.
Pacheco (2012) afirma que o ábaco é importante para o entendimento dos números decimais, bem como para a aprendizagem das operações de soma e subtração.
Software educativo
Com o avanço tecnológico, são inúmeros jogos que surgem no mercado com objetivo de auxiliar na educação. Acompanhar o avanço da tecnologia e fazer uso delas é uma forma de aproveitar os recursos disponíveis. Conforme Pereira e Cordenonsi (2009), os softwares garantem uma aprendizagem mais significativa, uma vez que, o manuseio é motivador.
O jogo mostrado a seguir é gratuito e tem o objetivo de trabalhar cálculos mentais, sendo utilizado em tablets ou celulares. Esse jogo permite exercitar a Matemática nas suas quatro operações (adição, subtração, multiplicação e divisão) de uma forma simples, prazerosa e divertida, possibilitando um aprendizado diferente do convencional. Segundo Barreto e Barbosa (2018), aulas nesse modelo diferenciado estimulam os alunos ao aprendizado.


Figura 3: Software educativo
Fonte: Peaksel Games, 2022.
O jogo Math Duel permite uma disputa entre duas pessoas, e os jogadores devem escolher uma entre três alternativas de cálculo que aparecerão. O jogo utiliza o cálculo mental ao trabalhar as quatro operações da Matemática. Acertando dez respostas, o competidor vence e muda de nível, aumentando sua pontuação. Quanto mais rápido o competidor fizer o cálculo da operação proposta no jogo, maior é a chance de ser um vencedor, conforme a Figura 3.
Material didático reciclado
O material didático pode ser produzido utilizando-se materiais recicláveis e são muitas as possibilidades para sua construção. A Figura 4 mostra oito rolos de papel higiênico envolvidos por cartolina colorida e numerados de 0 a 7. Dentro de cada rolo, palitos de picolé com operações de soma e subtração para serem efetuadas pelo aluno (Grupo Mão Criativa, 2015).
Após o cálculo, o aluno identifica o palito ao número correspondente que está no rolo e deposita o palito no rolo. Essa é uma forma de trabalhar a soma, bem como, a subtração. Além de trabalhar, também, com as operações de multiplicação e divisão.

Figura 4: Material didático reciclado
Fonte: Grupo Mão Criativa, 2015.
Esses materiais podem ser produzidos também pelos pais, em casa, como forma de brincadeira. Com isso, as crianças podem reproduzir e internalizar o conteúdo dado pelo professor em sala de aula.
Outra opção simples e considerada de fácil produção é o boliche de garrafa PET, apresentado na Figura 5. Consiste em enumerar as garrafas com uma caneta e, usando uma bola, a criança derruba as garrafas. Depois disso, a criança conta os pontos obtidos. O total de pontos é a soma dos números nas garrafas que foram derrubadas a cada jogada (Marinho; Camargo, 2015).

Figura 5: Boliche com garrafa PET
Fonte: Tempojunto - Marinho e Camargo, 2015.
Diana e Conti (2012) afirmam que, além de ser uma atividade prazerosa e lúdica, o boliche de garrafa pet proporciona a coordenação motora ao arremessar a bola, bem como trabalha a soma e a posição. A cada pontuação, a posição do aluno muda. Tudo isso contribui para melhorar a capacidade de raciocínio lógico do aluno, promovendo a sua interação e desenvolvendo as suas habilidades motoras.
Contudo, o material didático manipulável por si só não vai fazer com que o aluno aprenda. É relevante o papel do professor na escolha do material mais adequado e na apresentação do conteúdo em sua sala de aula.
Metodologia da pesquisa
A metodologia qualitativa de pesquisa permitiu encontrar as informações e as respostas para as questões norteadoras (Martins, 2004). A pesquisa bibliográfica foi elaborada utilizando ferramentas de buscas como Google Acadêmico e SciELO.
Na pesquisa de campo, utilizou-se o Google Formulário com a aplicação de um questionário para a obtenção de informações relevantes acerca da realidade das aulas de Matemática.
O questionário, conforme o Quadro 1, foi aplicado online a dez professores da Educação Básica, seis da rede pública do município de Campos dos Goytacazes e quatro da rede particular do município de Bom Jesus do Itabapoana. Esse questionário contém quatorze questões sobre a formação profissional dos professores (série em que trabalham, tempo de trabalho em sala de aula, dificuldades apresentadas pelos alunos, tipo de material didático que estão acostumados a trabalhar com os alunos e o porquê da escolha do material utilizado em sala de aula).
Quadro 1: Pesquisa com professores da Educação Básica nas aulas de Matemática
Questionário |
|
1 – Qual a sua formação profissional?
|
|
2 – Formação em quê? |
|
3 – Em qual rede de ensino você trabalha?
|
|
4 – Se escolheu a opção outros, qual? |
|
5 – Com qual série você trabalha? |
|
6 – Há quanto tempo você trabalha com Matemática em sala de aula? |
|
7 – Em sua experiência de sala de aula, quais as principais dificuldades apresentadas pelos alunos na aprendizagem da Matemática? |
|
8 – Como estão sendo as aulas no período de pandemia?
|
|
9 - Se escolheu a opção outros, qual? |
|
10 - Quais materiais didáticos você utiliza em sua aula de Matemática?
|
|
11 - Se escolheu a opção jogos, quais jogos? Se escolheu a opção outros, quais? |
|
12 – De acordo com o que você respondeu na Questão 10, diga o motivo da escolha desse material didático para ensinar Matemática. |
|
13 – Você acredita que o uso do material didático nas aulas de Matemática facilita a compreensão do conteúdo? Sim, por quê? Não, por quê? |
|
14– Caso sinta necessidade, você pode fazer mais comentários abaixo. |
|
A análise dos dados
Os dados obtidos nesta pesquisa têm o objetivo de esclarecer como os professores, tanto da escola pública quanto da privada, enxergam o baixo desenvolvimento dos alunos da Educação Básica no que se refere ao ensino-aprendizagem da Matemática.
Além disso, os dados permitiram verificar quais recursos foram utilizados pelos professores participantes desta pesquisa como facilitadores do trabalho no processo de aprendizagem dos alunos.
As respostas obtidas no questionário aplicado aos professores definiram a rede de ensino, a formação, o tempo de trabalho como professor, bem como, os materiais utilizados na sala de aula e anos/séries. Para facilitar a compreensão das informações obtidas nos questionários, os professores foram identificados individualmente por meio da numeração de um até dez.
Inicialmente, procurou-se saber qual a formação dos professores e, conforme o Gráfico 1, 100% dos professores são graduados, 50% são pós-graduados e 20% são mestres.
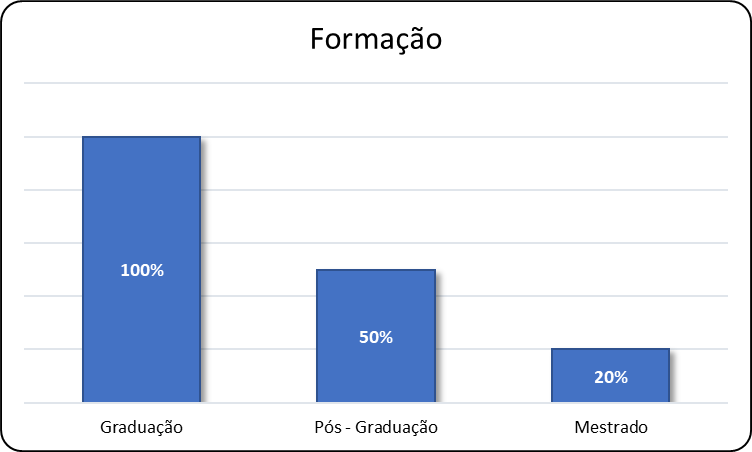
Gráfico 1: Grau de formação dos professores
O Gráfico 2 mostra qual a rede de ensino dos professores. Pode-se visualizar que a maioria dos professores (60%) é da rede pública.

Gráfico 2: Rede de atuação dos professores
Com relação ao tempo de trabalho dos professores em sala de aula foram obtidas as seguintes respostas: o menor tempo foi de três anos, seguido de quatro anos de experiência, sete e nove anos. Dois professores trabalham há mais de onze anos e o que trabalha há mais tempo tem 23 anos de experiência em educação.
Conforme o Gráfico 3, 60% dos professores trabalhavam de forma híbrida, 40% dos professores de forma virtual e 10% trabalhavam na modalidade presencial. Durante a pandemia, as escolas continuaram atendendo os alunos para que não ficassem sem aulas, pensando sobre as melhores maneiras de atendê-los até que retornassem de forma definitiva ao presencial.
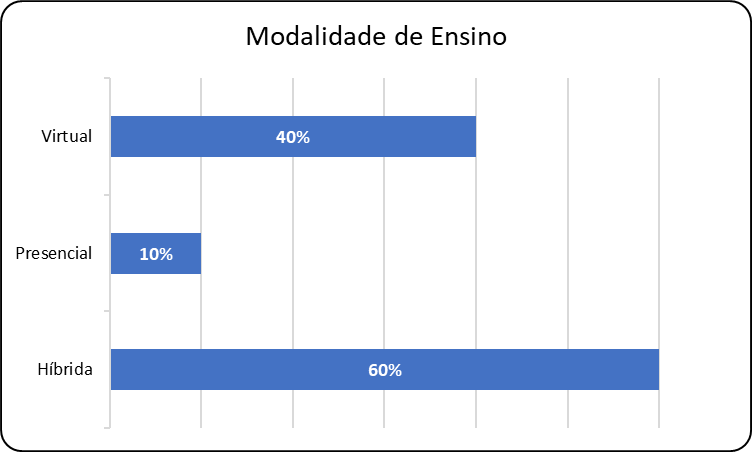
Gráfico 3: Forma de atuação na pandemia
Dando continuidade à análise das respostas obtidas no questionário, verifica-se que, em relação às dificuldades apresentadas pelos alunos, os professores afirmam que eles apresentam falta de conhecimentos prévios ou pré-requisitos necessários para o sucesso da aprendizagem de um novo conteúdo matemático.Além disso, os alunos não conseguem compreender nem interpretar os problemas propostos. Os alunos apresentam dificuldades na tabuada, nas operações de divisão e usam incorretamente o conceito de probabilidade e estatística. Todas as respostas obtidas foram representadas no Gráfico 4, com o respectivo percentual.
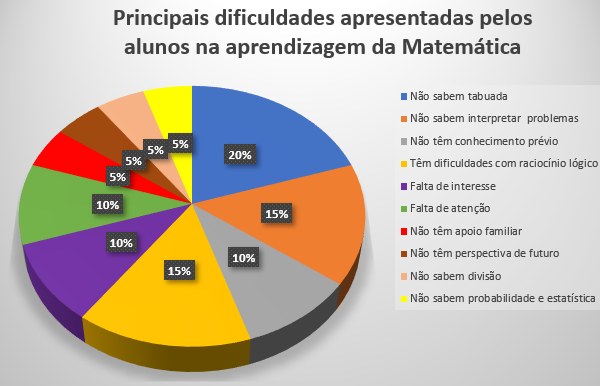
Gráfico 4: Principais dificuldades
Uma das perguntas do questionário refere-se ao ano do Ensino Fundamental ou à série do Ensino Médio em que trabalhavam nas escolas. Analisando as respostas obtidas, visualizadas no Gráfico 5, conclui-se que 20% dos professores entrevistados trabalhavam no Ensino Fundamental I, 80% no Fundamental II e 40% no Ensino Médio.
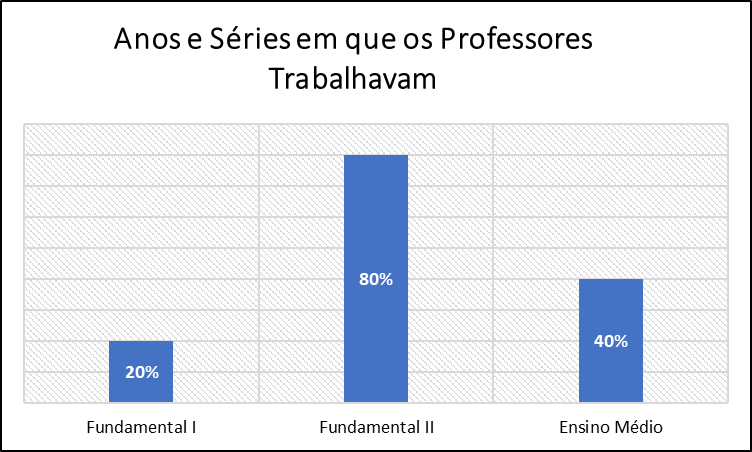
Gráfico 5: Níveis escolares de atuação
Os professores participantes da pesquisa foram questionados sobre o tipo de material didático que utilizavam em sala de aula para facilitar a compreensão do conteúdo. A análise das respostas obtidas nessa questão está representada no Gráfico 6: 32% utilizavam jogos, outros 32% trabalhavam com figuras geométricas, 23% usavam material dourado, 4% utilizavam ábaco e 9% outras ferramentas para auxiliar na aula.
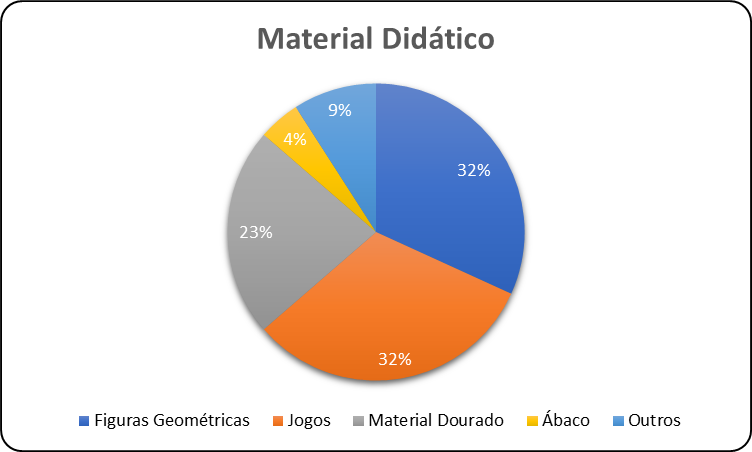
Gráfico 6: Materiais utilizados
Ainda com relação ao Gráfico 6, os professores apontaram que os jogos facilitam a aprendizagem do aluno, porque se aproximam mais da realidade desses alunos, tornando as aulas mais dinâmicas e a interação aluno/professor mais próxima.
Analisando as respostas da Questão 12, conclui-se que a maioria dos professores afirma que os jogos despertam na geração atual, um interesse maior pela disciplina, pois os estudantes ficam atentos durante o processo de aprendizagem. O importante é aproximar o conteúdo ensinado em sala de aula da realidade em que vivem os alunos.
Na Questão 13, em sua maioria os professores afirmaram que, ao utilizar materiais didáticos diversos, conforme o conteúdo a ser ensinado e a necessidade da aula, perceberam que esses materiais melhoraram a forma de apresentação do conteúdo, levando os alunos a aprender com a dinâmica e a gostar de utilizar outras formas de aprendizagem (sem ser o livro).
Somente dois docentes responderam à questão livre. Um deles registra que, com a experiência, observou que o ensino tradicional traz mais resultados em comparação ao ensino atual. Já a outra resposta aponta para o uso do celular. Segundo esse professor, as crianças passam muito tempo de posse de um aparelho celular; portanto, ele vê a importância de envolver essa ferramenta no ensino da Matemática. É importante relatar o fato de que, nos dias de hoje, muitos professores mencionam a falta de atenção como uma justificativa para a dificuldade de aprendizagem. O professor 5 observa que os celulares consomem mais a atenção das crianças do que qualquer outro meio.
Considerações finais
Este artigo mostra que a utilização de um recurso didático manipulável, tecnológico ou não, adequado ao conteúdo trabalhado, permite diversificar e aprimorar a forma de ensinar. Além disso, contribui para uma aproximação entre professor e aluno, estimulando o processo de abstração do aluno e possibilitando seu progresso ao longo da vida.
A pesquisa de campo realizada com a aplicação de um questionário aos professores foi um ponto importante, permitindo aos professores que expusessem suas ideias e experiências. A maioria dos entrevistados apontou que trabalhar com materiais manipuláveis facilita na aprendizagem da Matemática. Os jogos, que são uma realidade para o aluno, proporcionam ainda um maior interesse durante o processo de aprendizagem.
Destacamos o comentário do professor 6, ao citar o apoio familiar como “importante para o aluno, pois quando há incentivo e cobrança por parte dos responsáveis o aluno tende a ter uma busca maior pelo conhecimento”. Ou seja, não há dúvidas de que a família pode colaborar com o desenvolvimento escolar do aluno.
Alguns professores participantes da pesquisa relataram que os alunos apresentam a falta de conhecimentos prévios, pré-requisitos necessários e exigidos para o sucesso da aprendizagem de um novo conteúdo matemático.
Além disso, não saber tabuada, não conseguir interpretar os problemas, a falta de interesse e a desmotivação dos alunos são considerados empecilhos para o desenvolvimento de novos conceitos matemáticos.
Com o passar do tempo é possível o surgimento de métodos de ensino mais eficientes, outros materiais didáticos de apoio, bem como, a conscientização da comunidade escolar acerca da necessidade de explorar outros recursos para a melhoria da prática do professor em sala de aula a fim de promover o favorecimento da aprendizagem dos alunos.
Referências
BARRETO, Liliane Silva Faria; BARBOSA, Nelson Machado. Aplicativos gratuitos como ferramenta tecnológica no desenvolvimento do cálculo mental: uma metodologia lúdica para o Ensino Fundamental. Remat: Revista Eletrônica da Matemática, v. 4, n° 1, p. 115-131, 2018. Disponível em: https://dev7b.ifrs.edu.br/site_periodicos/periodicos/index.php/REMAT/article/view/2750. Acesso em: 25 jun. 2022.
BERNARDI, Giliane; CORDENONSI, Andre Zanki; SCOLARI, Angélica Taschetto. O desenvolvimento do raciocínio lógico através de objetos de aprendizagem. Renote - Revista Novas Tecnologias na Educação,v. 5, n° 2, 2007. Disponível em: https://www.seer.ufrgs.br/index.php/renote/article/view/14253/8169. Acesso em: 31 maio 2022.
BRASIL. MEC. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: introdução aos parâmetros curriculares nacionais. Brasília: MEC/SEF, 1997. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro01.pdf. Acesso em: 30 maio 2022.
BRASIL. MEC. Base Nacional Comum Curricular. Brasília: MEC, 2018, Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 28 ago. 2020.
BROSSI, Patrícia. Dificuldades de aprendizagem na Matemática: um estudo de intervenção pedagógica com crianças do Ensino Fundamental. Revista Mais Educação, São Caetano do Sul, v. 4, n° 3, 2021. Disponível em: https://www.revistamaiseducacao.com/artigosv4-n3-maio-2021/45. Acesso em: 29 jun. 2021.
DIANA, Viviane Biason Gomes; CONTI, Keli Cristina. A importância do jogo de boliche no auxílio à aprendizagem de Matemática dos alunos do 1º ano do Ensino Fundamental. Divers@!, v. 5, n° 2, 2012. Disponível em: https://revistas.ufpr.br/diver/article/view/34167/21284. Acesso em: 1 jun. 2022.
EDUCADOR. Ábaco de pino. Canal do Educador. 2021. Disponível em: https://educador.brasilescola.uol.com.br/estrategias-ensino/abaco.htm. Acesso em: 6 abr. 2021.
FIORENTINI, Dario. A pesquisa e as práticas de formação de professores de Matemática em face das políticas públicas no Brasil. Boletim de Educação Matemática, v. 21, n° 29, p. 43-70, 2008. Disponível em: https://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/1718. Acesso em: 01 jun. 2022.
GASPERI, Wlasta Nadieska Huffner; PACHECO, Edilson Roberto. A história da Matemática como instrumento para a interdisciplinaridade na Educação Básica. Pedagogia em Foco, n° 7, 2018. Disponível em: http://ead.bauru.sp.gov.br/efront/www/content/lessons/37/e2t1.pdf. Acesso em: 30 maio 2022.
GELLERT, Uwe. Didactic material confronted with the concept of mathematical literacy. Educational Studies in Mathematics, v. 55, n° 1, p. 163-179, 2004. Disponível em: https://www.jstor.org/stable/4150306. Acesso em: 01 jun. 2022.
GRUPO MÃO CRIATIVA. Estimule as operações matemáticas brincando. 2015. Disponível em: https://grupomaocriativa.wordpress.com/2015/11/20/estimule-as-operacoes-matematicas-brincando/. Acesso em: 02 jun. 2021.
INSTITUTO NACIONAL DE ESTUDOS E PESQUISAS EDUCACIONAIS ANÍSIO TEIXEIRA (INEP). Brasil no Pisa 2018 [recurso eletrônico]. Brasília: INEP, 2020. Disponível em: https://download.inep.gov.br/publicacoes/institucionais/avaliacoes_e_exames_da_educacao_basica/relatorio_brasil_no_pisa_2018.pdf. Acesso em: 30 maio 2022.
LEUNG, Frederick Koon Shing. In search of an East Asian identity in mathematics education. Educational Studies in Mathematics, v. 47, n° 1, p. 35-51, 2001. Disponível em: https://sci-hub.se/10.2307/3483252. Acesso em: 01 jun. 2022.
MA, Liping. Knowing and teaching elementary mathematics: teachers’ understanding of fundamental mathematics in China and the United States. New Jersey: Lawrence Erlbaum Associates, 2010. Disponível em: https://www.taylorfrancis.com/books/mono/10.4324/9780203856345/knowing-teaching-elementary-mathematics-liping-ma. Acesso em: 31 maio 2022.
MARINHO, Patrícia; CAMARGO, Patrícia. Tempojunto: Jogo de boliche caseiro. São Paulo, 2015. Disponível em: https://www.tempojunto.com/2015/10/06/como-fazer-boliche-de-garrafa-pet/. Acesso em: 02 jun. 2021.
MARQUES, Lidiane Macena; SIMIÃO, Lucélio Ferreira. Iniciação à docência: uma experiência de ensino com o uso do material dourado. EGRAD, Anais... v. 1, n° 2, 2011. Disponível em: https://anaisonline.uems.br/index.php/egrad/article/view/829. Acesso em: 31 maio 2022.
MARTINS, Heloisa Helena de Souza. Metodologia qualitativa de pesquisa. Educação e Pesquisa, São Paulo, v. 30, n° 2, p. 289-300, maio/ago. 2004. Disponível em: https://www.scielo.br/j/ep/a/4jbGxKMDjKq79VqwQ6t6Ppp/?format=pdf&lang=pt. Acesso em: 01 jun. 2022.
MENEZ, Mikaele Pereira Medeiros de; LIMA, Thiago Amaral Melo. As dificuldades de aprendizagem da Matemática na Educação Básica e seus reflexos no curso de licenciatura em Física do IFCE - Campus Tianguá. Remat: Revista Eletrônica da Matemática, Bento Gonçalves, v. 7, nº 2, e2001, 2021. DOI: 10.35819/remat2021v7i2id4560. Disponível em: https://periodicos.ifrs.edu.br/index.php/REMAT/article/view/4560/2863. Acesso em: 23 maio 2022.
OLIVEIRA, Paula Cristina et al. Uma rota pelos instrumentos de cálculo. História da Ciência e Ensino: Construindo Interfaces, v. 20, p. 787-801, 2019. Disponível em: https://revistas.pucsp.br/index.php/hcensino/article/view/46073/31043. Acesso em: 1 jun. 2022.
PACHECO, Ana Luisa Viana. O papel de materiais concretos na compreensão do sistema de numeração decimal. 2012. Disponível em: https://repositorio.ufmg.br/bitstream/1843/VRNS-9QMHD4/1/o_papel_de_materiais_concretos_na_compreens_o_do_sistema_de_.pdf. Acesso em: 1 jun. 2022.
PEAKSEL GAMES. Math Due. 2022. Disponível em: https://play.google.com/store/apps/details?id=com.mathduel2playersgame.mathgame&hl=pt_BR&gl=US. Acesso em: 25 jun. 2022.
PEREIRA, Lisandra Locatelli; CORDENONSI, André Zanki. Softwares educativos: uma proposta de recurso pedagógico para o trabalho de reforço das habilidades de leitura e escrita com alunos dos anos iniciais. Renote - Revista Novas Tecnologias na Educação, v. 7, n° 3, p. 196-208, 2009. Disponível em: https://seer.ufrgs.br/index.php/renote/article/view/13587/8556. Acesso em: 1 jun. 2022.
PIAGET, Jean. Psicologia Genética. Buenos Aires: Emecé, 1973.
PINTEREST. Material dourado. Disponível em: https://br.pinterest.com/pin/770115605010057991/. Acesso em: 27 mar. 2021.
RODRIGUES, Fredy Coelho; GAZIRE, Eliane Scheid. Reflexões sobre uso de material didático manipulável no ensino de Matemática: da ação experimental à reflexão. Revista Eletrônica de Educação Matemática, v. 7, nº 2, p. 187-196, 2012. Disponível em: https://periodicos.ufsc.br/index.php/revemat/article/view/1981-1322.2012v7n2p187/23460. Acesso em: 01 jun. 2022.
RODRIGUES, Renato de Oliveira Noronha. Material dourado no ensino das quatro operações básicas. 2012. Disponível em: https://www.ibilce.unesp.br/Home/Departamentos/Matematica/material-dourado-no-ensino-das-quatro-operacoes-basicas.pdf. Acesso em: 01 jun. 2022.
SILVA, Ana Cristina Almeida. O ensino da Matemática no Ensino Fundamental: a importância da relação professor e aluno para a aprendizagem. 2015. 53f. Monografia (Licenciatura em Matemática), Núcleo de Educação a Distância, Universidade Federal do Maranhão, 2015. Disponível em: https://rosario.ufma.br/jspui/bitstream/123456789/1199/1/AnaSilva.pdf Acesso em: 31 maio 2022.
SILVA, Dalmo Rodrigues da. Ábaco: prática pedagógica matemática. 2022. Disponível em: https://dspace.uniceplac.edu.br/bitstream/123456789/1327/1/%C3%81baco%20-%20pr%C3%A1tica%20pedag%C3%B3gica%20matem%C3%A1tica.pdf. Acesso em: 01 jun. 2022.
SILVA, Emerson Carlos; BENIGNO, Tayara Crystina Pereira. Laboratório de ensino-aprendizagem de Matemática: um espaço para as implicações na formação de educadores. 2012. Disponível em: https://www.editorarealize.com.br/artigo/visualizar/1207. Acesso em: 31 maio 2022.
SOUSA, David Anthony. How the brain learns mathematics. 2ª ed. California: Corwin, 2015.
SOUSA, Marcos Aurélio da Silva; SILVA, Flávio Soares da. Aprendizagem matemática nos anos iniciais do Ensino Fundamental: dificuldades. III CONEDU. Anais... Campina Grande: Realize, 2016. Disponível em: https://www.editorarealize.com.br/index.php/artigo/visualizar/20268. Acesso em: 25 maio 2022.
VASCONCELOS, Cláudia Cristina. Ensino-aprendizagem da Matemática: velhos problemas, novos desafios. Revista Millenium, v. 20, p. 2023-2026, 2000. Disponível em: http://www.dma.ufv.br/downloads/MAT%20102/2015-I/listas/Texto%2023-03%20-%20MAT%20102%20-%202015-I.pdf. Acesso em: 31 maio 2022.
VYGOTSKY, Lev. Pensamento e linguagem. São Paulo: Martins Fontes, 2008.
Publicado em 30 de maio de 2023
Como citar este artigo (ABNT)
SOUZA, Jorge Luiz Alves de; AGUIAR, Eliane Vigneron Barreto. Contribuições para a aprendizagem da Matemática na Educação Básica. Revista Educação Pública, Rio de Janeiro, v. 23, nº 20, 30 de maio de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/20/contribuicoes-para-a-aprendizagem-da-matematica-na-educacao-basica
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

