Multiplicação Oriental: passo a passo para aplicação matemática em sala de aula
Daniel Trevisan Sanzovo
UENP - Câmpus de Jacarezinho, doutor em Ensino de Ciências e Educação Matemática
Vanessa Queiroz
SESC – Jacarezinho/PR, mestra em Ensino de Ciências e Educação Matemática
Multiplicação significa “somar o mesmo número algumas vezes” (Volderman et al., 2012, p. 18), gerando um produto. Pelo viés semiótico, aconselha-se que não se confunda o objeto matemático com a sua representação (Machado, 2003). A compreensão conceitual, segundo Duval (2012, p. 282), “repousa sobre a coordenação de ao menos dois registros de representação e esta coordenação se manifesta pela rapidez e espontaneidade da atividade cognitiva de conversão”. Nessa perspectiva, a utilização de múltiplas representações (que variam de textual verbal e não verbal, escrito, tabela, imagem, gráfico, 3d, dentre outras) pode contribuir para que o aprendiz atribua um significado mais profundo ao conceito científico em questão (Trevisan Sanzovo, 2017).
Dessa maneira, ao recorrermos para a adição a outras metodologias de ensino (tais como aula tradicional, além de uso de material didático, do lúdico, da tábua de Pitágoras, dentre outras), há uma prioritariamente imagética, intuitiva e de fácil manipulação: a da Multiplicação Oriental. Ela é o foco do presente texto e pode ser oferecida ao aluno para uma aprendizagem efetiva das operações matemáticas de multiplicação.
Portanto, o presente texto tem como objetivo introduzir didaticamente a metodologia da Multiplicação Oriental para professores e aprendizes (praticamente de qualquer idade) da Educação Básica.
Passo a passo da Multiplicação Oriental
A Multiplicação Oriental é resumida passo a passo no presente texto pelas seguintes etapas:
- representar os números, por meio de semirretas inclinadas,
- identificar e separar as regiões de interseção,
- contar as interseções,
- realizar ajustes finais, caso necessário, e
- obter o resultado da operação.
A metodologia proposta se inicia com a etapa de representar os números envolvidos na multiplicação, por meio de semirretas diagonais perpendiculares entre si, formando entre elas, o “x” da multiplicação. A Figura 1 ilustra como estruturar a multiplicação 12 x 21 pelo método oriental, ilustrando a representação em (a) do número 12 (em verde) e, em (b), do número 21 (em azul).
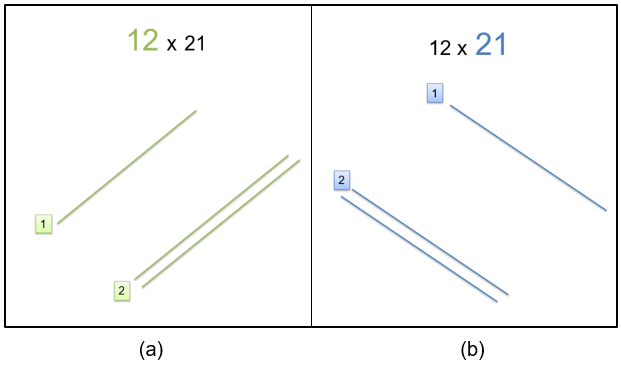
Figura 1: Representação dos números (a) 12 e (b) 21, para a multiplicação 12 x 21
Dessa forma, a estruturação da multiplicação 12 x 21 é ilustrada pela Figura 2.
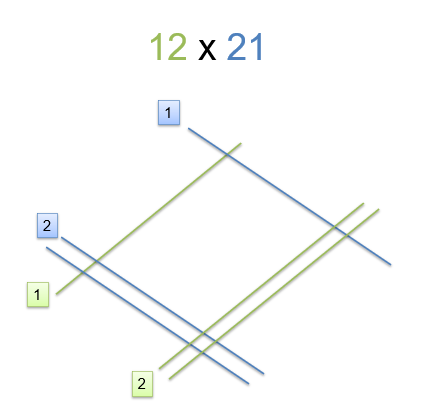
Figura 2: Representação da multiplicação 12 x 21
Assim, tomando como exemplo a multiplicação de 121 por 2.131, a etapa ficaria conforme a ilustração da Figura 3.
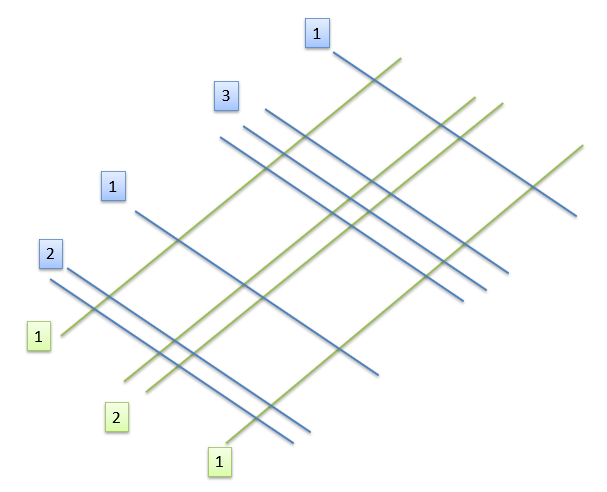
Figura 3: Representação da multiplicação 121 x 2.131
Na etapa seguinte, para identificar e separar as regiões de interseção, é preciso primeiramente identificar o que podemos chamar de “regiões verticais de interseção”, começando pelas regiões da extrema direita (“ponta da direita”) e, depois, da esquerda (“ponta da esquerda”), conforme ilustrado pela Figura 4.
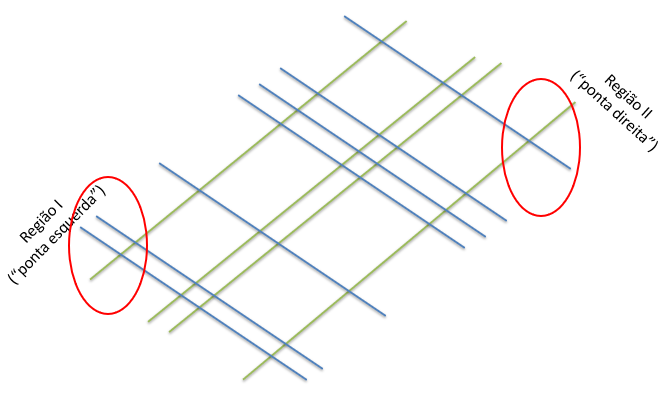
Figura 4: Identificando as regiões “ponta esquerda” (região I) e “ponta direita” (região II) da multiplicação 121 x 2.131
Percorra a linha superior verde da região I (que representa a centena do número 121) para a direita até encontrar a próxima interseção, como visto na Figura 5 (a). Ao encontrá-la, teremos a primeira “região vertical de interseção”, nossa “região III”, conforme ilustra a Figura 5 (b).
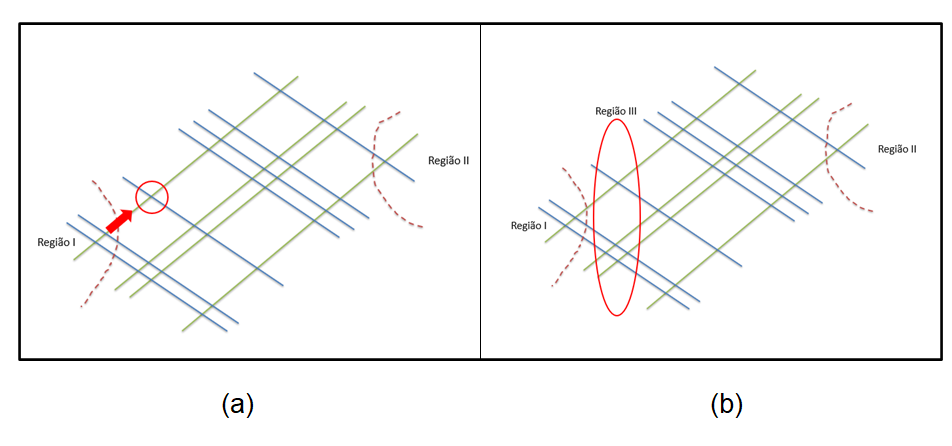
Figura 5: Identificando a primeira região vertical de interseção (região III) da multiplicação 121 x 2.131
Analogamente, encontram-se as regiões IV e V, conforme ilustram as Figuras 6 e 7.
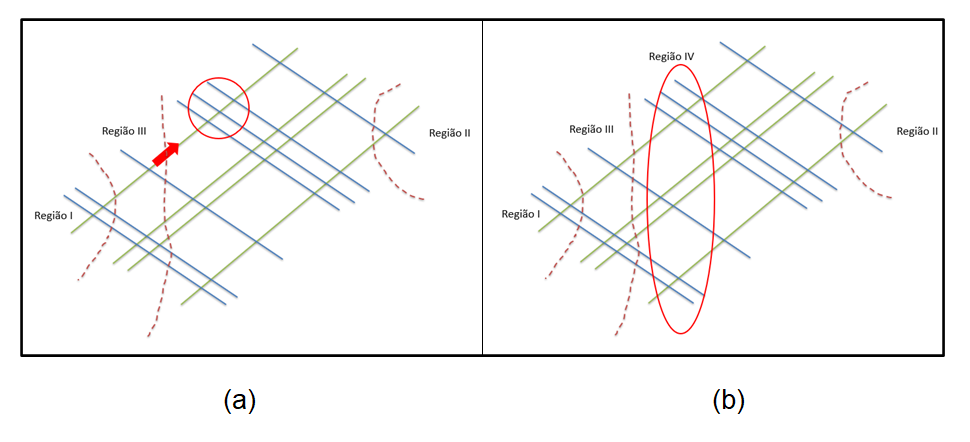
Figura 6: Identificando a segunda região vertical de interseção (região IV) da multiplicação 121 x 2.131
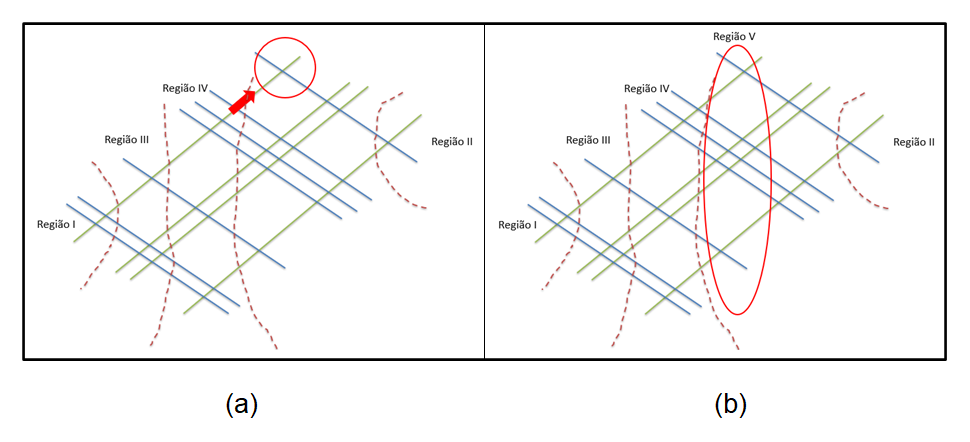
Figura 7: Identificando a terceira região vertical de interseção (região V) da multiplicação 121 x 2.131
Ao terminar de percorrer todas as interseções da linha superior verde da região I (que representa a centena do número 121), continue percorrendo a da linha abaixo (que, no caso, seria a dezena do número 121), conforme ilustra a Figura 8, e assim sucessivamente até que todas as regiões sejam identificadas.
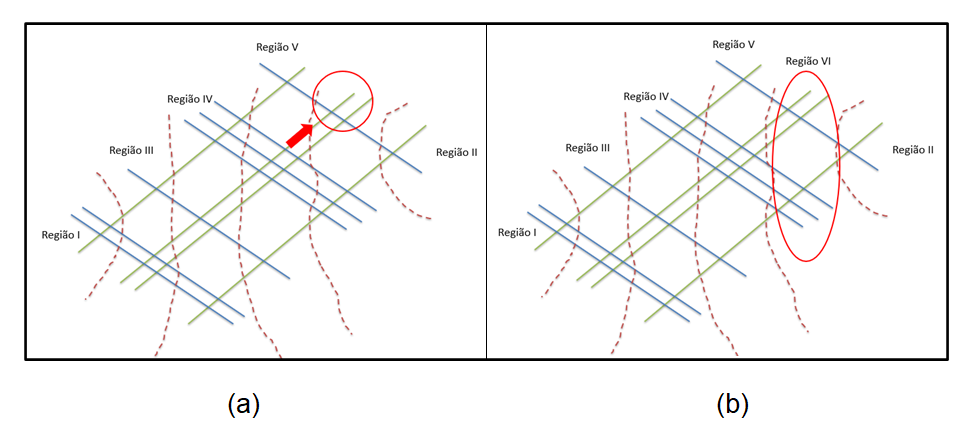
Figura 8: Identificando a quarta região vertical de interseção (região VI) da multiplicação 121 x 2.131
Após a identificação de todas as regiões, basta contar as interseções de cada região. A Figura 9 ilustra essa etapa para a multiplicação em questão (121 x 2.131).
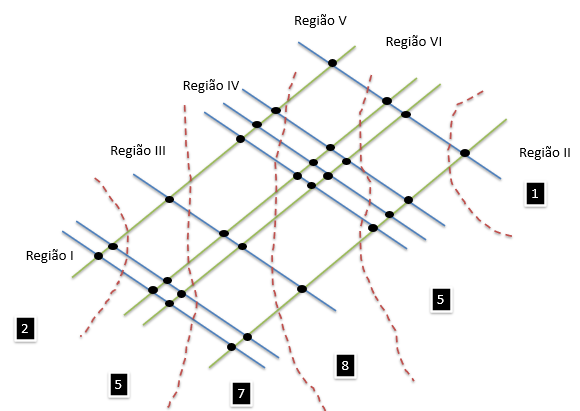
Figura 9: Contando as interseções das regiões da multiplicação 121 x 2.131
Note que, para o exemplo da multiplicação de 121 x 2.131, as regiões de interseções resultaram apenas em números posicionais de unidades (da esquerda para a direita da Figura 9: “2” na região I, “5” na região III, “7” na região IV, “8” na região V, “5” na região VI, e “1” na região II), não precisando de qualquer ajuste, passo (iv) do processo (que será visto adiante). Dessa maneira, já indica o resultado da operação: 121 x 2.131 = 257.851.
Mas quantas regiões de interseção temos por multiplicação?
A identificação das regiões tende a ser o passo mais complexo do método. Para tanto, sugere-se que, no início de sua jornada com a utilização do método, sejam utilizadas folhas grandes (como uma página inteira de papel sulfite) que represente os números bem espaçados entre si em cada operação de multiplicação. Além disso, é possível prever quantas regiões de interseção teremos para cada operação de multiplicação a ser realizada pela relação dada pela equação 1.
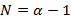 , (Equação 1)
, (Equação 1)
em que:
N = número de regiões de interseção;
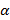 = número de algarismos envolvidos na operação de multiplicação.
= número de algarismos envolvidos na operação de multiplicação.
Assim, para o exemplo mencionado, temos a multiplicação de 121 (3 algarismos) por 2.131 (4 algarismos). Desse modo, o número de algarismos envolvidos na multiplicação é de
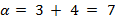 ; portanto, o número de regiões de interseção é de
; portanto, o número de regiões de interseção é de
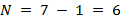 regiões.
regiões.
Vejamos, agora, um segundo exemplo: a multiplicação 34 x 51. De antemão temos um número de algarismos envolvidos na multiplicação de
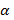 = 4 e o número de regiões de interseção será de
= 4 e o número de regiões de interseção será de
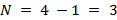 . A Figura 10 ilustra como ficam as etapas já elencadas para o presente caso.
. A Figura 10 ilustra como ficam as etapas já elencadas para o presente caso.
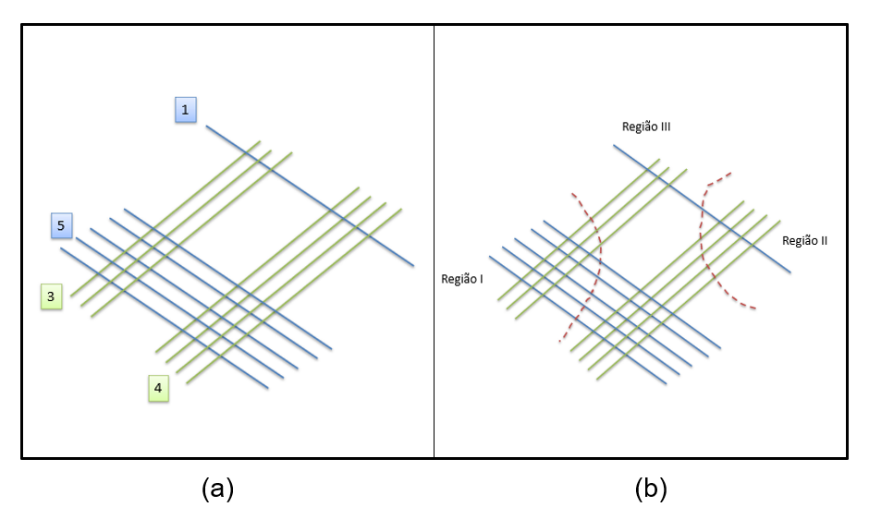
Figura 10: (a) Representação e (b) identificação das regiões, para a operação 34 x 51
Ao contarmos as interseções das regiões para o presente exemplo, temos, na região III, números posicionais de dezenas, além de unidades (número “23”). Dessa maneira, o passo ajustes finais se faz necessário, deixando o valor posicional das unidades (o número “3”) na própria região e somando o valor posicional das dezenas (o número “2”) ao número da região próxima da esquerda (número “15”), conforme mostra a Figura 11 (e isso deve ser feito com todas as regiões de interseção verticais até chegarmos à região da ponta esquerda). Dessa maneira, temos como resultado da operação 34 x 51 = 1.734.
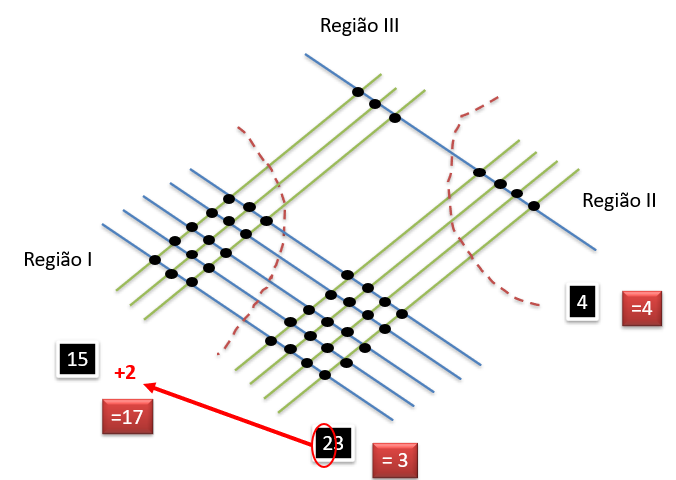
Figura 11: Ajustes finais para a operação 34 x 51
Caso de multiplicação com número que contenha zero
Ao utilizarmos o método com número que contenha zero, o que muda é que não se deve contar nenhuma interseção com a linha que representará o zero. Sugere-se ainda representar o zero do número com linha diferenciada (cores diferentes e/ou tracejado). Por exemplo, na operação 102 x 123, a Figura 12 ilustra como devemos representar e identificar as respectivas regiões (linha tracejada de verde).
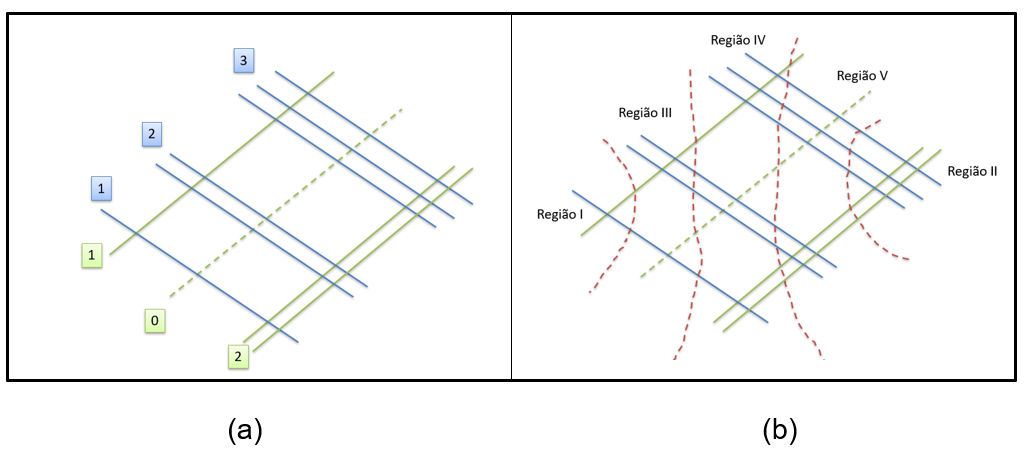
Figura 12: (a) Representação e (b) identificação das regiões, para a operação 102 x 123
Dessa forma, ao realizarmos a contagem das interseções, não se deve contabilizar nenhuma interseção com a linha que representa o zero do número 102, conforme ilustra a Figura 13. Dessa maneira, temos como resultado da operação 102 x 123 = 12.546.
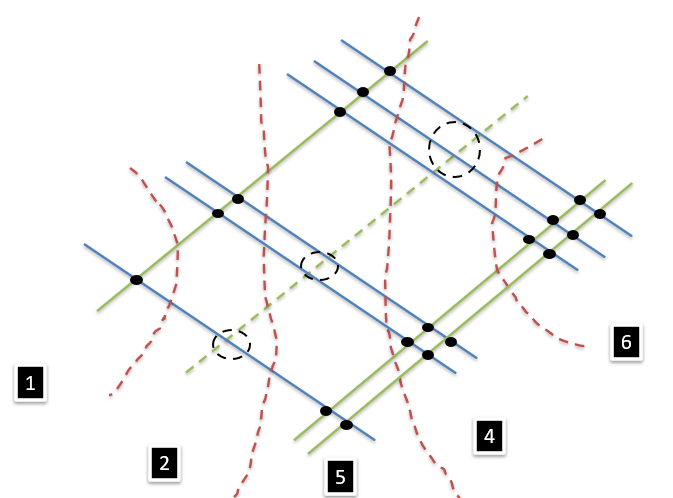
Figura 13: (a) Representação e (b) identificação das regiões, para a operação 102 x 123
Caso de multiplicação com número que contenha vírgula
Para o caso de multiplicação com número que contenha vírgula, o que muda é que a operação deve ser realizada ignorando a vírgula. Na etapa de ajustes finais, deve-se verificar o número de casas decimais envolvidas na operação e contar esse número no resultado. Por exemplo, na multiplicação 1,3 x 2,4 temos duas casas decimais envolvidas na operação: “3” do número 1,3 e “4” do número 2,4). Dessa forma, deve-se contabilizá-las no resultado, conforme ilustrado pela Figura 14: 1,3 (uma casa decimal) x 2,4 (uma casa decimal) = 3,12 (duas casas decimais). Portanto, temos como resultado da operação 1,3 x 2,4 = 3,12.
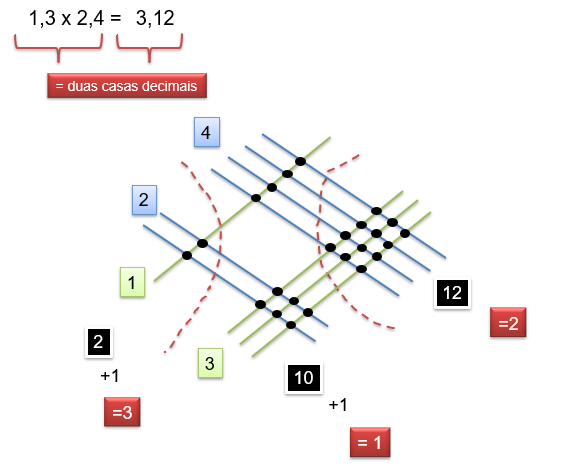
Figura 14: Multiplicação Oriental para o caso de números com vírgulas (operação 1,3 x 2,4)
Caso especial de aplicação: tabuada
Um caso específico para a utilização da Multiplicação Oriental é o da tabuada, que pode fornecer ao aprendiz uma aprendizagem efetiva da operação básica da multiplicação, fugindo da tradicional decoreba. Para o caso da tabuada do número 4, por exemplo, a Figura 15 ilustra como podemos utilizar o método para seu aprendizado. Para a sua construção, sugere-se a utilização de cores diferenciadas e manufaturadas em conjunto com seus alunos.
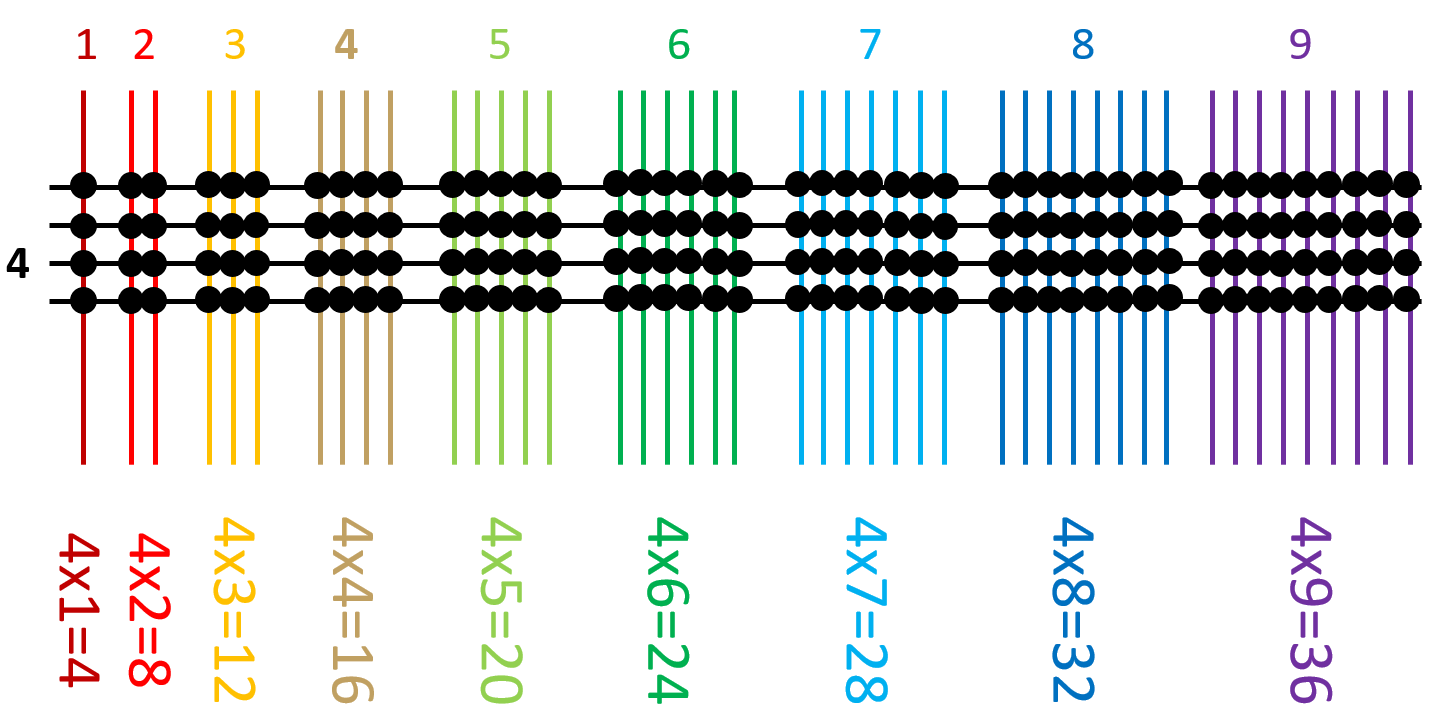
Figura 15: Multiplicação Oriental para a tabuada do número 4
Considerações finais
Propondo uma divulgação formal do denominado método da Multiplicação Oriental, o presente trabalho teve como objetivo ilustrar as principais etapas dessa metodologia, auxiliando o professor e o estudante com o estudo matemático. Destarte, em adição o texto exemplifica de maneira clara e intuitiva a utilização do método e ainda traz uma aplicação para o seu uso no estudo da tabuada.
A presente metodologia tem se mostrado eficaz tanto na aplicação para a Educação Básica e para o Ensino Superior de licenciandos, quanto para os cursos ministrados de formação continuada para professores em exercício. Com isso, se mostra interessante como auxílio para o estudo das operações matemáticas, especialmente da multiplicação.
Referências
DUVAL, Raymond Registros de representação semiótica e funcionamento cognitivo do pensamento. Revista Eletrônica de Educação Matemática, v. 7, n° 2, 2012.
MACHADO, S. D. A (org.). Aprendizagem matemática: Registros de representação semiótica. Campinas: Papirus, 2003.
TREVISAN SANZOVO, D. Níveis interpretantes alcançados por estudantes de licenciatura em Ciências Biológicas acerca das estações do ano por meio da utilização da estratégia de diversidade representacional: uma leitura peirceana para sala de aula. 2017. 192f. Tese (Doutorado em Ensino de Ciências e Educação Matemática) – Universidade Estadual de Londrina, Londrina, 2017.
VOLDERMAN, C. et al. Matemática para pais e filhos. São Paulo: Publifolha, 2012.
Publicado em 06 de junho de 2023
Como citar este artigo (ABNT)
TREVISAN SANZOVO, Daniel; QUEIROZ, Vanessa. Multiplicação Oriental: passo a passo para aplicação matemática em sala de aula. Revista Educação Pública, Rio de Janeiro, v. 23, nº 21, 6 de junho de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/21/multiplicacao-oriental-passo-a-passo-para-aplicacao-matematica-em-sala-de-aula
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

