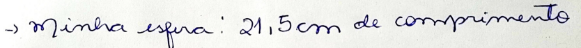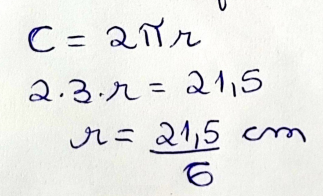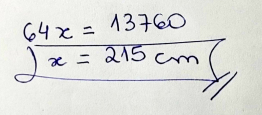A curiosidade como motor do aprendizado: reflexões a partir da elaboração de uma maquete honesta
Daniela Mendes Vieira da Silva
Doutora, professora adjunta na UERJ
Abel Rodolfo Garcia Lozano
UERJ
Marcele Câmara de Souza
UERJ
Priscila Cardoso Petito
UERJ
Fábio Menezes
UERJ
Carolina Oliveira Lopes
UERJ
Alex Sander da Silva Alves
UERJ
O presente relato de experiência apresenta reflexões e propostas de melhoria de um experimento de baixo custo reelaborado a partir de notas de uma aula, do Programa de Pós-Graduação em Ciências e Matemática da Universidade Federal Rural do Rio de Janeiro (UFRRJ), vivenciada pela primeira autora na condição de discente, feito em um contexto de formação continuada de professores. A experiência envolve razão e proporção e distâncias astronômicas na construção de uma surpreendente maquete honesta do sistema Terra-Lua. Tais reflexões e modificações foram feitas a partir da vivência, no contexto de um projeto de pesquisa, elaborado na Faculdade de Formação de Professores da Universidade do Estado do Rio de Janeiro (FFP/UERJ) e coordenado pela primeira autora, denominado Instrumentalização do Laboratório de Matemática e Física do Colégio Estadual Walter Orlandine e sua Replicação em Malas Sustentáveis. Tal projeto é fomentado pela Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (Faperj), no Edital Faperj nº 45/21 – Apoio à melhoria das escolas da rede pública sediadas no Estado do Rio de Janeiro - 2021.
Oferecer alternativas pedagógicas exequíveis e de baixo custo que ao mesmo tempo tenham intencionalidade pedagógica e Matemática à comunidade que se debruça sobre o aprendizado desta disciplina, como defendem Silva, Arquieres e Menezes (2018), é de vital importância para o fortalecimento não só da comunidade acadêmica envolvida com pesquisas nesse campo de saber, mas sobretudo do professor ou professora que busca alternativas viáveis para a sua prática diária. Ademais, mostrar que a Matemática é utilizada em outras ciências, como a Astronomia, como indica o nosso experimento, ajuda a desmistificar a equivocada crença popular de que ela é isolada e tem pouco uso prático. Quem nunca ouviu a pergunta “Quando irei usar Matemática na minha vida?”.
Para além dessas intencionalidades, é necessário pensar em atividades que despertem a curiosidade dos aprendentes, uma vez que sem motivação não se aprende, como afirmam Silva, Andrade e Nascimento (2019). O prazer de descobrir move o ser humano; as pessoas são curiosas, haja vista o sucesso de tabloides de todo tipo, noticiando até mesmo as menores banalidades da família real do Reino Unido ou os bilionários números do mercado aquecido de influencers de todo o mundo, os quais vendem a exposição de seu dia a dia, e o sucesso certo de programas de confinamento, nos quais é possível, seja pela TV aberta, seja pela TV paga, acompanhar o dia a dia de desconhecidos e/ou de subcelebridades. Toda essa sede de saber pode ser estimulada para motivar estudantes no contexto da educação científica. Essa é uma das premissas da oficina ora analisada.
Portanto, como objetivo geral buscamos apresentar de maneira assertiva dados e observações gerados por participantes do experimento da maquete honesta vivenciado em uma oficina oferecida e reelaborada no contexto do projeto supracitado.
O primeiro objetivo específico é compartilhar com a comunidade acadêmica uma proposta curiosa, interdisciplinar e teoricamente pensada de construção do conceito de razão e proporção dentro da Astronomia. O segundo é apresentar os dados coletados e as observações feitas pelos participantes envolvidos e, a partir desses dados e observações, constituir inferências no sentido de discutir a contribuição do experimento em foco para o aprendizado de Matemática. O terceiro é reformular, com base nos dados apresentados, na investigação em sala de aula de Ponte (2003) e na Teoria dos Registros de Representação Semiótica de Duval (2009), a oficina proposta aqui.
Este artigo possui, além desta introdução, revisão de literatura, metodologia, relato assertivo, considerações finais, referências e agradecimentos.
Revisão de literatura
O ser humano é movido pela curiosidade, seja para saber a última notícia, seja para criar ferramentas que facilitem o seu dia a dia. É dentro dessa premissa que se insere a investigação em sala de aula; a partir de Ponte (2003), entendemos que
- a aula deve sempre se iniciar a partir de uma situação curiosa;
- os estudantes devem criar suas próprias hipóteses para o fenômeno observado;
- caminhos para que elas sejam testadas devem ser trilhados;
- em caso de sucesso nesses testes, a solução do fenômeno deve ser apresentada a toda a turma;
- em caso de insucesso, é necessário retornar ao segundo passo, elaborar uma nova hipótese e prosseguir para os passos seguintes.
A investigação em sala de aula propicia aos aprendentes um ambiente no qual o conhecimento pode ser construído de forma ativa; nesse ambiente, ao invés do/da docente estar o tempo todo convencendo os estudantes de que tal conteúdo merece ser decorado, de forma repetitiva e declaratória, ele incita os alunos a buscarem suas próprias descobertas. Tal não ocorre de forma aleatória e sem direcionamento. Pelo contrário, o/a docente deve, para que tal ambiente seja de fato vivenciado, criar as condições para que a investigação esperada ocorra e que os participantes construam o conceito em foco, sem desvios nem perda de foco. Isso é um desafio, uma vez que a perda do controle da turma em atividade criativa pode ocorrer com muita facilidade, haja vista a dificuldade de concentração inerente à geração atual.
Carr (2010) alerta que a vida moderna, hiperconectada, traz como efeito colateral uma geração que não se aprofunda nem se detém por muito tempo em nenhum tema. Segundo esse autor, com a velocidade da circulação da informação e com os estímulos sensoriais positivos decorrentes da navegação incessante de link em link, as pessoas com acesso à internet têm se mantido cada vez mais no raso, na superfície, se atendo à leitura muitas vezes apenas do título de um texto, compartilhando-o rapidamente e indo em busca do próximo link.
Um exemplo deste comportamento é o sucesso do Tik Tok, uma rede de vídeos curtos que duram de segundos a pouquíssimos minutos, e a propagação desse formato em outras redes que inicialmente não tinham esse foco, como o Instagram com seus reels e o YouTube com seus shorts.
Não só o entretenimento, mas também toda sorte de interação na grande rede passa por essa ânsia incontrolável de imediatismo; a partir de Santaella (2010), afirmamos que a interação na interneté ubíqua, ou seja, ela é permanente, caótica e desenfreada; tal urgência se transpõe para a vida real daqueles que interagem na grande rede.
Nesse sentido, um ambiente que utilize a internet e essa necessidade por novidades pode se constituir como alternativa para superar a superficialidade e levar os estudantes ao necessário aprofundamento requerido para que o aprendizado de fato aconteça.
Portanto, a educação científica se mostra uma alternativa para desenvolver o aprendizado não só de Matemática, mas de outras disciplinas, de forma integrada, ativa e aprofundada no ambiente escolar; ao quebrar a compartimentalização disciplinar e fomentar atividades integradas, torna-se facilitada a questão tantas vezes levantada: “professor, quando vou usar esse conteúdo na minha vida?”.
Também serve para mostrar que a Matemática é uma construção humana, muitas vezes dedicada à solução de problemas reais e que ela dá suporte a outras ciências e pode se configurar em uma porta de entrada para a curiosidade em sala de aula.
Mas investigar pressupõe organização e uma atuação do/a professor/a proponente que não iniba os estudantes de criar seus próprios caminhos, mas também não os deixe à própria sorte em suas investigações.
Com Vygotsky (2000), entendemos que a distância entre o que o aprendente consegue produzir sozinho e o que o aprendente consegue produzir com apoio, a chamada zona de desenvolvimento proximal, é um fenômeno social. Portanto, para o sucesso do aprendizado de todos os envolvidos, a postura do/a professor/a ao oferecer apoio sem dar respostas prontas, encaminhar ações e tirar dúvidas é fundamental em uma sala de aula na qual se vivencia um ambiente investigativo. A metodologia Steam – em uma tradução livre, sigla para Ciência, Tecnologia, Engenharia, Artes e Matemática – traz essa perspectiva integrada e curiosa para a sala de aula, segundo Lemes (2022, s/p):
a forma de ensino faz não só a integração das áreas do conhecimento, mas permite ao aluno usá-las para conexões na hora de resolução de problemas diários. O aprendizado é amplamente beneficiado com a interdisciplinaridade. Além disso, nesse processo de ensino os alunos aprendem a colaborar uns com os outros. É papel importante do professor ser o mediador dessa nova proposta pedagógica. Ele deve trazer os alunos a entender como aprender fazendo; a educação dessa forma fica mais desafiadora e atrativa.
Mas, para além de estimular a curiosidade dos aprendentes e de criar um ambiente investigativo interdisciplinar, no qual eles tenham caminhos orientados para fazer suas próprias descobertas, é necessário fazer com que tal ambiente seja cognitivamente econômico, matematicamente falando, para que todos possam se beneficiar dele.
Subsidiando o trabalho de professores que ensinam Matemática com este desiderato, temos a Teoria dos Registros de Representação Semiótica (TRRS), de Duval (2009). A partir desse autor, entendemos que evitar a confusão entre objeto matemático (o qual é inacessível aos sentidos) e suas representações está no cerne da TRRS, uma vez que ela preconiza a necessidade de coordenação entre diferentes representações semióticas de um mesmo objeto matemático. Nessa teoria, a representação semiótica, ou seja, simbólica recebe o nome de Semiósis, e a coordenação de mais de uma representação semiótica de um mesmo objeto matemático recebe o nome de Noésis (Figura 1).
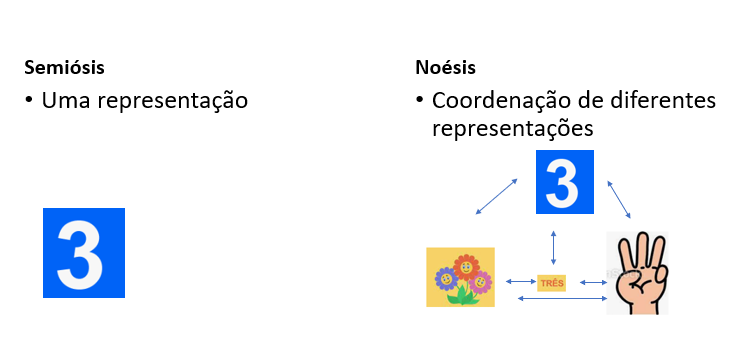
Figura 1: Semiósis e Noésis
Portanto, compreender que o número três, para citar um exemplo matemático previamente ilustrado, pode ser expresso por três dedos pela palavra três e por três flores, e que nenhuma dessas representações é o três em si, é fundamental para a compreensão do conceito estudado.
A compreensão de que diferentes representações semióticas de um mesmo objeto matemático se interconectam pode ser alcançada por meio de conversões entre diferentes suportes semióticos. A Figura 2 traz um exemplo de conversão.
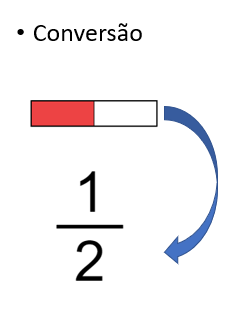
Figura 2: Conversão
A TRRS também prevê outro tipo de transformação; ela é denominada tratamento e se dá dentro do mesmo suporte semiótico, como ilustra a Figura 3.
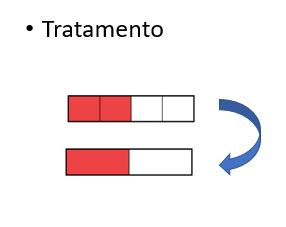
Figura 3: Tratamento
Cada suporte semiótico pode ser decomposto em elementos significantes, os quais são as menores unidades detentoras de sentido neles. Tal decomposição é fundamental para que sejam criadas conversões cognitivamente econômicas, as quais estão ligadas ao sucesso escolar. A Figura 4 traz um exemplo dessa decomposição.

Figura 4: Decomposição
Para criar uma conversão cognitivamente econômica é necessário que os suportes de partida e de chegada sejam decompostos em elementos significantes e que esses elementos significantes de partida e chegada se relacionem um a um, que tal relação ocorra na mesma ordem e que o suporte semiótico de chegada tenha entendimento único, inequívoco. A Figura 5 ilustra uma conversão cognitivamente econômica.
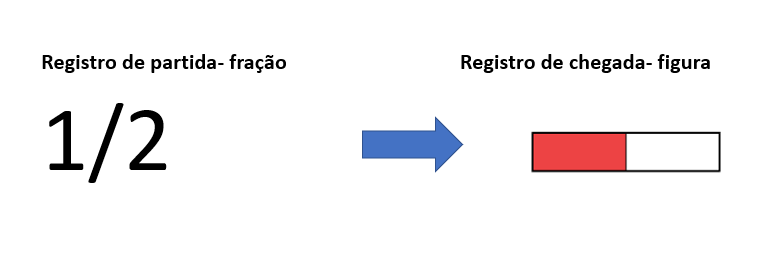
Figura 5: Economia cognitiva
Nota-se que o registro de partida pode ser decomposto em dois elementos principais: o primeiro é o número 1, que indica quantas partes temos, e o segundo é /2, que indica em quantas partes o nosso inteiro está dividido. O registro de chegada também pode ser decomposto em dois elementos principais: o primeiro é uma parte da barra pintada em vermelho e o segundo é que a barra está dividida em duas partes iguais. Cada elemento de partida se liga a um elemento de chegada na mesma ordem e o elemento de chegada é inequívoco; logo, essa é uma conversão econômica, que é o que buscamos na atividade em discussão.
Sujeitos e local de coleta de dados
Os sujeitos da atividade relatada aqui são quatro professores bolsistas de Treinamento e Capacitação Técnica (TCT) do projeto de pesquisa citado, neste texto denominados professores J, N, A e C. O local da experiência aqui relatada foi o Laboratório de Matemática e Física do Colégio Estadual Walter Orlandine (CEWO), o qual está sendo revitalizado e instrumentalizado com o fomento Faperj citado.
Atividade preparada
A atividade investigativa relatada aqui foi preparada coletivamente pela coordenadora, pelos professores associados e pelos bolsistas de Iniciação Científica do projeto. Ela tanto pode ser vivenciada por professores em formação inicial ou continuada quanto por estudantes da Educação Básica, porque consiste em uma proposta de atividade diferenciada e interdisciplinar para sala de aula. Para os primeiros, o foco da discussão reside nas suas possibilidades pedagógicas, matemáticas e científicas; para os estudantes, a discussão foca no seu aprendizado. Ela foi testada na reunião semanal dos bolsistas de Iniciação Científica no dia 3 de novembro de 2022 e foi oferecida aos professores bolsistas TCT no dia seguinte pela bolsista de Iniciação Científica Carolina, com a participação do bolsista extensionista Alex Sander, do projeto Laboratório de Ensino de Matemática da Faculdade de Formação de Professores da UERJ itinerante e de baixo custo, vinculado à Sub-Reitoria de Extensão e Cultura da UERJ (SR3), aprovado para o ano de 2022, coordenado pela primeira autora deste artigo.
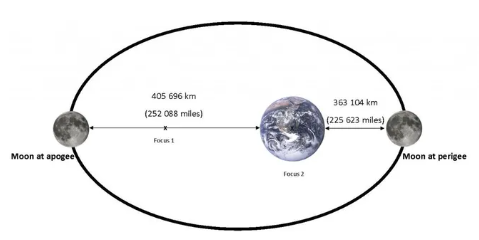
Trata-se do experimento da maquete honesta do sistema Terra-Lua. Os materiais necessários para a atividade são: os smartphones dos participantes, esferas de diferentes tamanhos, fitas métricas/trenas, papéis e lápis para anotação. Os participantes são divididos em tantos grupos quantas forem as esferas disponíveis. Para empreender a investigação, além da esfera, cada grupo recebe lápis, papel e uma fita métrica.
Na primeira etapa, é proposta a pergunta disparadora: “Considerando a esfera recebida como sendo a maquete da Terra, a que distância a Lua estaria nesse modelo, se a proporcionalidade entre o planeta e seu satélite natural fosse respeitada?”. Normalmente, nesse ponto os palpites situam a Lua, na maquete, a poucas dezenas de centímetros do modelo da Terra.
Na segunda etapa da investigação, é pedido aos participantes que determinem o raio da esfera recebida, utilizando para tanto a fita métrica. Caso os(as) participantes fiquem perdidos(as), é informado que o raio da esfera modelo pode ser calculado com C= 2πraio, onde C é o perímetro da circunferência – nesse caso, do equador do modelo.
Na terceira etapa da investigação, pede-se que participantes pesquisem, em valores aproximados, o raio real da Terra e a distância real entre Terra e Lua e que determinem a distância entre Terra e Lua no modelo recebido. Caso os participantes não tenham acesso à internet, informa-se que o raio da Terra tem aproximadamente 6.400km e a distância entre a Terra e a Lua é de aproximadamente 384.000km; pede-se que determinem a distância proporcional entre a Terra e a Lua no modelo.
Apenas caso os participantes fiquem perdidos, o dinamizador deve encaminhar o uso da regra de três no processo. O uso da calculadora é opcional, mas não deve ser desencorajado, uma vez que o foco está no experimento e não nas contas necessárias para levá-lo a cabo com sucesso. Nessa etapa, dentro da TRRS, temos tratamento, uma vez que os registros de partida e chegada usados estão em escrita algébrica.
Ao final dessa etapa da investigação, é esperado que os participantes se surpreendam ao perceber que a Lua, na maquete, fica muito mais distante do que todos imaginaram inicialmente. Para uma esfera de 16cm de raio representando a Terra na maquete, a Lua do modelo ficaria a cerca de 9,6m de distância.
Ao final, na quarta etapa da investigação, os participantes devem ser convidados a responder um formulário pensado para guiar a elaboração de um relatório da vivência, com orientações que buscam estabelecer uma reflexão sobre o tema trabalhado e consolidando a construção do conceito em questão. O relatório deve conter:
- Nome;
- Instituição;
- Objetivo do experimento;
- Plano elaborado para o alcance do objetivo;
- Dados coletados e forma de coleta;
- Resultados encontrados;
- Link para envio de arquivo dos dados coletados e dos resultados encontrados;
- Discussão do experimento: escrever se o objetivo foi alcançado, de que forma o plano elaborado concorreu para isso, destaque de limitações encontradas e possibilidades de desdobramentos futuros do experimento;
- Observações e sugestões para a melhoria do experimento vivenciado;
- Termo de Consentimento: ao clicar em sim, permito a utilização, sem a minha identificação, das atividades realizadas por mim no âmbito da atividade referente a este formulário. Estou ciente de que não haverá benefício direto para participar do estudo, além da retomada de reflexões sobre conceitos matemáticos e diferentes formas de ensiná-los. Ficou claro também que minha participação é isenta de despesas e que nada será pago por ela. Concordo voluntariamente em participar do estudo. Eu poderei retirar o meu consentimento a qualquer momento, sem penalidades ou prejuízos. ( ) sim ( ) não.
Relato assertivo
Da primeira etapa sobrevieram as observações esperadas, situando a Lua do modelo muito próxima da Terra do modelo, como esperado; isso ocorre porque é recorrente nas salas de aula brasileiras a confecção de modelos do Sistema Solar em uma folha de isopor, modelos que não têm preocupação com a proporcionalidade entre os astros representados. Com uma rápida busca na internet, é possível ter acesso a inúmeros desses modelos. Portanto, como o foco do presente trabalho é o aprimoramento da oficina, nossa discussão versará sobre as demais etapas, as quais discutimos na sequência.
Segunda etapa: raio do modelo
Nessa etapa, observamos que os professores envolvidos optaram pelo uso da escrita algébrica; não foram usados diagramas ou desenhos que ilustrem suas observações e estratégias. Adiante apresentamos e comentamos as produções dos professores N e C, as quais apresentaram cálculos separados para a etapa em seus registros escritos, o que não ocorreu para os professores J e A, os quais fizeram direto o cálculo do valor pedido.
O/A professor/a N apresentou passo a passo o cálculo do raio do “equador”, ou seja, da maior circunferência, da esfera recebida e decidiu escrever o resultado em forma de dízima periódica, ou seja, para esta professore o arredondamento se mostrou adequado ao pedido, e, de fato, uma vez que nada foi indicado nesse sentido na tarefa, realmente esse é um caminho possível para a etapa.
Já o/a professore C, que, assim como o/a professore N, também organizou passo a passo o seu caminho para o cálculo da distância pedida no modelo, optou por registrar o raio do modelo em forma fracionária. Isso mostra a opção do(a) docente por precisão em seus cálculos.
Como esperado, no contexto da investigação em sala de aula de Ponte (2003), os participantes devem ter autonomia para escolher seus próprios caminhos investigativos; isso fica claro a partir dos dados apresentados, uma vez que os participantes escolheram caminhos distintos para suas investigações.
Adiante observamos as produções de N e C.
Professore N |
Professore C |
|
|
|
Figura 6: Produções de N e C
Uma vez que a TRRS também guiou a elaboração da atividade, fica evidente, como sugestão de melhoria a partir dos dados coletados, a necessidade da indicação, no enunciado da etapa, do uso de ao menos dois suportes semióticos na apresentação das estratégias utilizadas para o cálculo do raio do modelo pedido. A partir de Duval (2002), entendemos ser fundamental estimular os participantes na utilização de desenhos e diagramas que ilustrem os caminhos trilhados por eles na resolução da tarefa proposta. E, mais do que isso, que, buscando a economia cognitiva, a congruência seja estimulada.
Essa etapa pode ser cognitivamente econômica se usar ao menos dois suportes semióticos, registro figural e escrita numérica e estabelecer uma ligação elemento significante de partida a elemento significante de chegada um a um, na mesma ordem, e cada elemento significante de chegada tem entendimento único, como indicado por Duval (2009).
A medição do equador, dentro da TRRS pensada para essa atividade, foi pensada para ser cognitivamente econômica, uma vez que ela usa dois suportes semióticos, o material concreto e a escrita numérica, e estabelece uma ligação elemento significante de partida a elemento significante de chegada um a um na mesma ordem, e cada elemento significante de chegada tem entendimento único. Isso está descrito no diagrama a seguir.
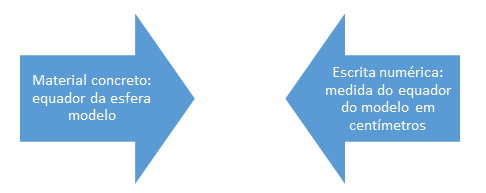
Já o cálculo do raio da esfera recebida é um tratamento, uma vez que nele os registros de partida e chegada estão no mesmo suporte semiótico, ou seja, a escrita algébrica. As produções dos(as) professores C e N se encaixam na proposta feita.
Terceira etapa: pesquisa de dados reais e cálculo da distância pedida no modelo
Os/As professores J e A usaram notação científica para expressar as distâncias dos astros reais analisados; trata-se de uma estratégia interessante quando se fala de distâncias astronômicas e que mostra conexão com a utilidade desse objeto matemático na Física. A seguir reproduzimo-las.
Professor J |
Professor A |
|
|
|
Figura 7: Produções de J e A
Esta etapa, a partir da estratégia dos(as) professores J e A, mostra que as produções des professores C e N trazem duas abordagens dentro da escrita algébrica para o cálculo da distância pedida; no desenvolvimento, C opta por utilizar frações e N por uma representação decimal de uma dízima periódica, conforme se pode observar abaixo.
Professorx C |
Professorx N |
|
|
Figura 8: Abordagens de C e N
Observamos aqui, em busca de melhorias para a atividade do ponto de vista da TRRS, a necessidade do pedido direto, no enunciado, do uso de mais de um suporte semiótico na etapa, uma vez que todos/as os/as participantes optaram pelo uso da escrita algébrica como único suporte semiótico. E, mais do que isso, tal pedido deve encaminhar a congruência na conversão entre tais suportes, uma vez que ela visa à aprendizagem científica de estudantes da Educação Básica ao final, e tal aprendizagem deve ser cognitivamente econômica para assegurar a compreensão conceitual dos envolvidos. É imperioso, para esse desiderato, estimular o uso de tabelas, diagramas e figuras na ilustração das estratégias adotadas pelos participantes. Uma opção de conversão cognitivamente econômica a ser proposta nessa etapa, pensada a partir dessas inferências, pode ser vista na Tabela 1.
Tabela 1: Dados em diferentes suportes de representação
Registro de partida |
Registro de chegada |
Representação figural |
Representação em escrita numérica (usando arredondamento) |
Fonte da imagem: Braz, 2022. |
______ km |
Fonte da imagem: Cassita, 2022. |
________ km |
Ao indicar a necessidade do uso de mais de um suporte semiótico ao participante da oficina, estimula-se a não confusão entre objeto matemático e representação, o que, segundo Duval (2009), é fundamental para o sucesso escolar em Matemática. Além disso, é necessário estabelecer uma relação direta na mesma ordem entre elementos de partida e chegada como elementos de chegada de entendimento único. Um caminho para que isso ocorra é a utilização de uma tabela, nos moldes da Tabela 1. Portanto, para futuras vivências, tal modificação será acrescentada.
Quarta etapa: reflexões
O encerramento da oficina se dá com o registro das reflexões dos participantes no formulário proposto; dois campos desse formulário se destacaram:
- O campo disponível para a entrega das imagens dos seus registros escritos, o qual se mostrou importante para o registro e organização dos dados coletados e para o acesso às estratégias empregadas por eles;
- O campo dedicado às observações e sugestões para a melhoria do experimento vivenciado. As reflexões dos professores referentes a ele são apresentadas e comentadas adiante.
O/A Professore A registrou a seguinte impressão:
Chegar à conclusão de que, com o uso do valor de Pi igual a 3, a distância entre a Terra e a sua Lua será sempre 10 vezes o valor da circunferência da Terra pode ser um elemento a mais para estudantes que consigam realizar essa experiência sem grandes dificuldades. Até mesmo analisando os resultados entre participantes se pode levantar a hipótese e através dos cálculos concluir sua validade.
Tal observação se mostrou profícua dentro da perspectiva de Ponte (2003), não só no sentido de levantar um questionamento pertinente à investigação, como também no sentido de incluir um novo questionamento no formulário que orienta a elaboração do relatório do experimento, o que traz uma melhoria clara à atividade proposta.
O/A Professore C trouxe a seguinte contribuição:
No desenvolvimento da atividade não mudaria nada. Ela é de fácil entendimento e está muito bem organizada. Só temos que ter o cuidado com o nível de abstração dos nossos alunos. Fico com medo de os alunos confundirem e trabalharem o comprimento da esfera como sendo o diâmetro. Acredito que o professor deverá ficar atento na sala para sanar essas dúvidas.
A partir do/a professore C, compreendemos ser importante alertar os participantes da atividade em foco sobre a diferença entre comprimento da maior circunferência da esfera e o seu diâmetro; tal modificação foi contemplada para a nova versão da atividade.
O/A Professore N trouxe duas ponderações para a atividade analisada, conforme se pode ver:
Medir a esfera foi um pouco complicado, pois a fita métrica escorregava. Minha sugestão é usar esferas em que o resultado da distância, que será utilizada na maquete honesta, caiba no local destinado à realização do experimento, para que não despertem nos participantes um sentimento de frustração.
A primeira ponderação diz respeito à dificuldade própria da medição de superfícies curvas; com base nessa observação entendemos ser importante destacar a necessidade de cuidado na medição, pela dificuldade inerente a ela. A segunda ponderação, aderente à investigação em sala de aula de Ponte (2003), por facilitar a etapa de validação da conjectura feita pelos participantes, também será acrescentada ao enunciado da atividade, uma vez que, caso o/a professore que a utilize não possa sair de sala de aula, ele/a deverá escolher esferas que resultem em distâncias para o modelo que possam ser medidas dentro de uma sala de aula.
O/A professore J traz uma sugestão que consideramos excelente, tanto dentro da perspectiva de Ponte (2003), por facilitar o momento de divulgação dos resultados obtidos, quanto da TRRS de Duval (2009), porque estimula o uso de um suporte semiótico para além da escrita algébrica e que adotamos para o fechamento da terceira etapa da investigação em sala de aula; é: “Sugestão é um projeto que inclua a montagem dessa maquete”. Os demais campos do formulário trouxeram respostas protocolares e precisam ser revistos, afora os de identificação, de forma que instiguem a reflexão dos participantes para além de um relato protocolar e expositivo.
Considerações finais
Como objetivo geral, buscamos documentar, de maneira assertiva, dados e observações gerados por participantes da atividade envolvendo o experimento da maquete honesta, vivenciado em uma oficina oferecida no contexto do projeto. Ele foi feito via formulário elaborado na conta Google do projeto Matemática e Física na Mala. Tal suporte se mostrou adequado, uma vez que permitiu não só o registro das reflexões dos participantes como também o da data de sua geração e seu armazenamento na nuvem do projeto.
O nosso primeiro objetivo específico foi compartilhar com a comunidade acadêmica uma proposta curiosa, teoricamente pensada, de construção do conceito de razão e proporção. Para tanto, descrevemos neste texto, em detalhe, a atividade aplicada aos professores participantes, de modo a facilitar a compreensão das vivências efetuadas e de seus desdobramentos.
O nosso segundo objetivo específico foi apresentar os dados coletados e as observações feitas pelos participantes envolvidos e, a partir desses dados e observações, constituir inferências no sentido de discutir a contribuição do experimento em foco para o aprendizado de Matemática e Física. Também esse objetivo foi alcançado, uma vez que não só os dados coletados foram apresentados como também foram apresentas as inferências que surgiram a partir da sua análise.
O nosso terceiro objetivo específico foi reformular, a partir dos dados apresentados e da Teoria dos Registros de Representação Semiótica, a oficina proposta. Esse objetivo também foi alcançado, uma vez que a oficina reformulada está disponível no anexo deste texto. Ela conta com observações para aplicadores cuja necessidade nasceu da leitura e análise das produções dos professores participantes da oficina aqui apresentada de forma assertiva.
Como limitações encontradas para o estudo, destacamos que a falta da indicação, no enunciado de cada etapa, da importância do uso de mais de uma representação semiótica na comunicação das estratégias traçadas por cada participante ao longo da oficina; isso foi corrigido na nova versão.
Como desdobramentos futuros, pretendemos nos debruçar sobre outras atividades vivenciadas no âmbito tanto do projeto de pesquisa Matemática e Física na Mala, fomentado pela Faperj, quanto do projeto de extensão LEM FFP UERJ Itinerante.
Referências
BRAZ, D. Duas voltas na Terra, e de carro! 2016. Disponível em: https://fisicanaveia.blogosfera.uol.com.br/2016/11/02/duas-voltas-na-terra-e-de-carro/. Acesso em: 30 nov. 2022.
CARR, N. The Shallows: What the internet is doing with our brains. Nova York: W. W. Norton, 2010.
CASSITA, D. Qual a distância da Terra à Lua. s/d. Disponível em: https://canaltech.com.br/espaco/qual-e-a-distancia-da-terra-a-lua-222304/. Acesso em: 30 nov. 2022.
DUVAL, R. Semiósis e pensamento humano – registros semióticos e aprendizagens intelectuais. Fascículo 1. São Paulo: Livraria da Física, 2009.
FUNDAÇÃO DE APOIO E DESENVOLVIMENTO AO ENSINO, PESQUISA E EXTENSÃO (FADEPE). Método científico: definições, aplicações, principais tipos e etapas. 2021. Disponível em: https://fadepe.org.br/2021/06/16/metodo-cientifico-definicoes-aplicacoes-principais-tipos-e-etapas/. Acesso em: 7 nov. 2022.
LEMES, D. Educação Steam: o que é, para que serve e como usar. 2022. Disponível em: https://j.pucsp.br/artigo/educacao-steam-o-que-e-para-que-serve-e-como-usar. Acesso em: 30 nov. 2022.
PONTE, J. P. Investigar, ensinar e aprender. ROFMAT. Actas... Lisboa: APM, 2003. p. 25-39.
SANTAELLA, L. A aprendizagem ubíqua substitui a educação formal? Revista de Computação e Tecnologia da PUC-SP, São Paulo, v. 2, nº 1, p. 17-22, out. 2010.
SILVA, D. M. V.; ARQUIERES, D. D.; MENEZES, F. Descobrindo, com embalagens descartadas, o que o seu produto preferido esconde de você. Revista Educação Pública, v. 18, nº 8, 17 abr. 2018. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/18/8/descobrindo-com-embalagens-descartadas-o-que-o-seu-produto-preferido-esconde-de-voc.
SILVA, D. M. V.; ANDRADE, F.; NASCIMENTO, I. A. Ideia intuitiva de limite usando o círculo e a circunferência. Revista Educação Pública, v. 19, nº 11, 11 de junho de 2019. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/19/11/ideia-intuitiva-de-limite-usando-o-circulo-e-a-circunferencia.
VYGOTSKY, L. S. A construção do pensamento e da linguagem. São Paulo: Martins Fontes, 2000.
Deixamos nossos agradecimentos à Faperj, fomentadora do projeto Matemática e Física na Mala, e à UERJ, universidade à qual o projeto de extensão LEM FFP Itinerante é vinculado. Também agradecemos à direção do Colégio Estadual Walter Orlandine pela parceria e a todos os bolsistas e professores associados aos projetos citados.
Apêndice: Guia remodelado
Na primeira etapa, os participantes devem responder à pergunta disparadora: “Considerando a esfera recebida como sendo a maquete da Terra, qual seria a distância que a Lua estaria desse modelo, se a proporcionalidade entre este planeta e seu satélite natural fosse respeitada?”.
Segunda etapa: os participantes devem calcular o raio da esfera recebida, utilizando fita métrica, lápis e papel.
Dicas para professores aplicadores:
Observação 1: Caso os(as) participantes fiquem perdidos(as), é informado que o raio da esfera modelo pode ser calculado com C= 2πraio, onde C é o perímetro da circunferência, neste caso, o equador do modelo.
Observação 2: Chame a atenção para o fato de que o perímetro da circunferência máxima é diferente do diâmetro da esfera.
Terceira etapa, primeira parte: os participantes devem pesquisar, em valores aproximados, o raio real da Terra e a distância real entre Terra e Lua. Esses dados devem ser organizados utilizando ao menos dois suportes semióticos.
Observação: Caso os(as) participantes não tenham acesso à internet, informa-se que o raio da Terra tem aproximadamente 6.400km e a distância entre a Terra e a Lua é de aproximadamente 384.000km; que determinem a distância proporcional entre a Terra e a Lua no modelo.
Terceira etapa, segunda parte: com os dados levantados, os participantes devem calcular a distância entre a Terra e a Lua para o modelo recebido.
Observação: Apenas caso os(as) participantes fiquem perdidos(as), o dinamizador deve encaminhar o uso da regra de três no processo. O uso da calculadora é opcional, mas não deve ser desencorajado, uma vez que o foco está no experimento e não nas contas necessárias para levá-lo a cabo com sucesso.
Terceira etapa, terceira parte: os(as) participantes devem criar uma maquete honesta, elaborada em detalhes e proporcional, a partir dos cálculos efetuados.
Observação: Caso o/a dinamizadore da atividade tenha que fazê-la em um espaço limitado, sem a possibilidade de uso do pátio da escola, por exemplo, ele/a deve escolher modelos que resultem em maquetes que caibam na sala de aula de aplicação da atividade.
Ao final, na quarta etapa, os(as) participantes são convidados(as) a responder um formulário pensado para guiar a elaboração de um relatório da vivência, com orientações que buscam estabelecer uma reflexão sobre o tema trabalhado e consolidando a construção do conceito em questão. Sua transcrição remodelada segue adiante, em tópicos.
- Nome;
- Instituição;
- Descreva, em suas próprias palavras, o objetivo do experimento. Utilize diagramas, tabelas e ilustrações para enriquecer o seu relato;
- Descreva, passo a passo, o plano elaborado por você para o alcance do objetivo. Seja o mais detalhista possível;
- Apresente aqui os dados coletados e forma como os coletou. Seja meticuloso(a) nesta apresentação e indique a ordem na qual tais dados foram coletados;
- Apresente aqui, em detalhes, e usando diferentes suportes, como tabelas, diagramas e ilustrações, os resultados encontrados por você em sua investigação;
- Envie, neste link o arquivo com as fotos das suas anotações manuais feitas com papel e lápis;
- Escreva aqui se o objetivo do experimento foi alcançado, de que forma o plano elaborado concorreu para isso, destaque limitações encontradas e possibilidades de desdobramentos futuros deste experimento;
- Escreva aqui suas observações e sugestões para a melhoria do experimento vivenciado;
- Termo de consentimento: ao clicar em sim, permito a utilização, sem a minha identificação, das atividades realizadas por mim, no âmbito da atividade referente a este formulário. Estou ciente de que não haverá benefício direto para participar do estudo, além da retomada de reflexões sobre conceitos matemáticos e diferentes formas de ensiná-los. Ficou claro também que minha participação é isenta de despesas e que nada será pago por ela. Concordo voluntariamente em participar deste estudo. Eu poderei retirar o meu consentimento a qualquer momento, sem penalidades ou prejuízos.
Publicado em 25 de julho de 2023
Como citar este artigo (ABNT)
SILVA, Daniela Mendes Vieira da; LOZANO, Abel Rodolfo Garcia; SOUZA, Marcele Câmara de; PETITO, Priscila Cardoso; MENEZES, Fábio; LOPES, Carolina Oliveira; ALVES, Alex Sander da Silva. A curiosidade como motor do aprendizado: reflexões a partir da elaboração de uma maquete honesta. Revista Educação Pública, Rio de Janeiro, v. 23, nº 28, 25 de julho de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/28/a-curiosidade-como-motor-do-aprendizado-reflexoes-a-partir-da-elaboracao-de-uma-maquete-honesta
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.