O ensino de frações nos cursos de Pedagogia: um estudo de caso

Considerando que cabe à escola oferecer aos alunos oportunidades para trocas entre sujeito/meio a fim de que avancem no desenvolvimento integral, o grande desafio hoje é fazer o aluno compreender o seu papel na sociedade como agente ativo e transformador da realidade. É fundamental, portanto, que ele observe a importância da Matemática para o seu dia a dia.

Para possibilitar a elaboração de um plano curricular, rico e eficaz, é necessário conhecer o processo de construção de conhecimento no aprendiz. Devemos com urgência repensar o currículo e formas facilitadoras para o ensino da Matemática. Nesse contexto, não podemos deixar de fora seus aspectos históricos, principalmente no ensino das frações, e suas operações algébricas, pois sabemos ser a área responsável pelos estudos da Ciência Matemática.

Números inteiros são abstrações que surgem do processo de contar coleções finitas de objetos, contudo, as necessidades da vida diária requerem, além da contagem de objetos individuais, a medição de várias quantidades. Para satisfazer essas necessidades básicas referentes às medições (dentre outras possibilidades), necessitamos da compreensão das frações. Raramente, elas são observadas por um único número inteiro e, por esse motivo, surge o conjunto dos números racionais como o quociente de dois números inteiros, o suficiente para os propósitos que contém todos os inteiros de todas as frações (Eves, 2004, p. 104).

A aprendizagem é um jogo de perdas e ganhos. Novas concepções se acoplam às outras e destroem antigas crenças. Os profissionais da educação precisam refletir mais sobre como os alunos constroem os conteúdos acadêmicos e o que esses conteúdos significam no processo geral de adaptação do sujeito à realidade.

Nesse momento, queremos chamar a atenção dos educadores sobre o quanto é prejudicial uma ação pedagógica alienante. As ações do sujeito são significadas pelo seu interesse por um determinado objeto de conhecimento. Quanto mais o estudante estiver motivado internamente para executar sua tarefa, mais condições ele terá de revelar a aplicabilidade de suas estruturas de conhecimento e evoluir cognitivamente.

Existem ainda outros grandes desafios, como por exemplo, a falta de apoio das instituições de ensino no sentido de viabilizar condições necessárias e suficientes às práticas de ensino alternativas. A própria desmotivação, por parte do professor que exerce uma carga excessiva de horas de trabalho, a falta de interesse dos alunos, a indisciplina, a falta de tempo para a elaboração de projetos alternativos de ensino, a resistência por parte de outros professores da área “acostumados” com o ensino tradicional e, principalmente, as novas tecnologias, pois elas obrigam a uma mudança metodológica de ensino. O programa do currículo é previamente estabelecido não dando muitas vezes a oportunidade de o professor variar sua metodologia, sendo necessário “cumprir” com o programa (tantas vezes inflexível).

Para podermos facilitar o processo de ensino-aprendizagem da Matemática, principalmente no ensino das operações com números fracionários, precisamos nos valer de metodologias que aproximem a teoria da prática. Com essas junções, criamos saberes e possibilidades para a área de ensino, pois a sua aprendizagem é um dos entraves, bem como a sua complexidade, afastando não só o professor (que deve ser esse agente transformador do processo), mas principalmente os alunos, que percebem, na atuação do professor, aspectos de insegurança e desconhecimento.

A Matemática se desenvolveu no tempo com seus significados e suas abstrações. Nesse sentido, acredita-se que eles têm feito com que o professor repense sua prática pedagógica, para que possa ser esse agente transformador. Muitos são os caminhos oferecidos para o estudo das operações algébricas com números fracionários de forma mais prazerosa e mais significativa na relação entre a Ciência Matemática e os alunos. Contudo, para ocorrer um ganho real, precisamos reduzir a distância entre os conceitos algébricos e o professor e do professor em relação aos seus aprendizes. Nesse momento, podemos nos amparar nas novas tecnologias para reconfigurar as formas de descobrir um novo aprender, pois quanto mais o aluno aprende, mais vontade ele tem de caminhar sobre novos saberes.

Mas será que os professores têm procurado caminhos que possibilitem essa aproximação? A inquietação sobre o ensino das operações algébricas com frações para os alunos e as alunas do curso de Pedagogia nos fez pesquisar o tema a fim de entender as lacunas existentes entre o aprendizado e o exercício pedagógico do ensino. Vários foram os motivos que estimularam a ver essas operações com outros olhos e vários foram os módulos que nos fizeram refletir, não só sobre a prática docente matemática, mas também sobre a verificação das dificuldades que os alunos apresentam quando estão estudando os conceitos das operações nos processos algébricos, principalmente quando números fracionários estão envolvidos.

Ao trabalharmos os conceitos algébricos são fundamentais: aliar o tema a ser escolhido com a realidade de nossos alunos e aproveitar as experiências extraclasses dos alunos aliadas à experiência do professor em sala de aula. O professor precisa levar aos seus alunos mais desafios do que soluções. Nesse sentido, as novas tecnologias digitais ofertadas ao ensino têm sido de grande valia para que o professor possa fazer pontes entre o que seus alunos aprendem intelectualmente em situações reais vividas, pois assim sua aprendizagem será mais viva e enriquecedora.

Podemos enumerar os diversos benefícios de trabalharmos com as novas tecnologias digitais: motivação do aluno e do próprio professor, e para que isso aconteça e de suma importância que o mesmo se conscientize de que essa aprendizagem fará diferença na vida desses alunos e principalmente na sua; facilitação da aprendizagem, o conteúdo matemático passa a ter significação, deixa de ser abstrato e passa a ser concreto, e para que isso aconteça o professor tem que procurar se atualizar na busca desses novos saberes; verificamos também que as operações algébricas com os números fracionários ajuda na preparação para futuras áreas do conhecimento matemático, principalmente na interdisciplinaridade e na interatividade do conteúdo matemático com outras disciplinas; desenvolvimento do raciocínio, lógico e dedutivo em geral; o desenvolvimento do cálculo mental; compreensão do papel sociocultural da matemática, tornando-a assim, mais importante.

Este texto pretende abordar a questão da construção do conhecimento algébrico e suas implicações pedagógicas numa abordagem do ensino crítico e questionador, dando destaque ao discurso que a Educação Matemática privilegia como agente facilitador, assim como as metodologias ofertadas às aprendizagens desses conceitos, principalmente por meio das tecnologias digitais e da construção de modelos. Como objeto final, permitir que os alunos participem dessas novas descobertas.

Baseado nas premissas descritas acima e nas observações sobre as melhoras formas de ensinar as frações, procuramos fazer paralelos entre as formas tradicionais de ensino e o uso das tecnologias a fim de construir esses novos saberes. Para isso, nos valeremos da teoria e da prática sobre as quais elas foram discutidas nos diferentes módulos do curso de Mestrado Profissional em Novas Tecnologias Digitais na Educação. Buscando essa excelência, usaremos a tecnologia disponível como agente facilitador do ensino e da aprendizagem e, finalmente, ofereceremos a oportunidade de os alunos construírem seus próprios conhecimentos algébricos e suas operações com números fracionários.

Justificativa

Este trabalho surgiu da necessidade de levar ao Ensino Básico, por parte dos pedagogos, conceitos algébricos que acabam não sendo abordados de forma significativa para a aprendizagem dos alunos. O que precisamos mais frequentemente é dar maior ênfase a esse ensino, especialmente, aos conceitos algébricos. Para isso, aliamos as tecnologias ao lúdico, buscando uma aprendizagem mais interessante e com significado.

O que observamos em sala de aula nas turmas de Pedagogia é a falta de conhecimentos necessários para a realização de práticas pedagógicas significativas. Em nossa caminhada pedagógica, observamos que grande parte dos livros didáticos exclui os diferentes axiomas e tipos de aplicações práticas, reduzindo a “meia dúzia de fórmulas banais do mundo físico” (Gazire, 2000). Consequentemente, esse cenário pode contribuir para acentuar a dificuldade na compreensão dos alunos dos conceitos algébricos.

O computador está provocando uma verdadeira revolução no processo ensino-aprendizagem. O advento do computador na educação provocou o questionamento dos métodos e da prática educacional. O computador deve ser utilizado como um canalizador da mudança do paradigma educacional. Um novo paradigma que promove a educação, ao invés do ensino, e coloca o controle do processo da aprendizagem nas mãos do aprendiz. Isso auxilia o professor na compreensão de que a educação não é somente a transferência de conhecimento, mas um processo de construção, como produto de seu engajamento intelectual (Valente, 2002).

Por fim, os conceitos algébricos estão no cotidiano dos alunos. Por isso, faz-se necessário inseri-los de forma eficaz no Ensino Básico. Ou seja, é preciso que o aluno compreenda o mundo em que vive e do qual faz parte. Daí a importância do estudo da Álgebra, particularmente dos números fracionários. Esse estudo pode ocorrer não só por meio de softwares disponíveis, mas também pela utilização de materiais concretos, pois tornarão a aprendizagem muito mais prazerosa e interessante.

Segundo Papert (1988), os ambientes informatizados apresentam-se como ferramentas de grande potencial frente aos obstáculos inerentes ao processo de aprendizagem. É a possibilidade de mudar os limites entre o concreto e o formal.

O computador permite criar um tipo de objeto – os objetos concreto-abstratos. Concretos porque existem na tela do computador e podem ser manipulados. E abstratos por serem realizações feitas a partir de construções mentais (Gravina, 1998).

Por esses motivos existe a necessidade de escolher bem os recursos que poderão ser utilizados, sejam softwares ou materiais concretos, pois servirão de ferramentas na construção da aprendizagem significativa dos conceitos algébricos. Nesse sentido, a Matemática permite a inferência dessas tecnologias como formas de encurtar espaços e tempos.

Objetivos

O objetivo geral deste trabalho de pesquisa é fazer com que os alunos dos cursos de Pedagogia possam (re)conhecer a importância, bem como, a necessidade de ensinar as operações algébricas, com números fracionários, por meio das tecnologias digitais e, também, com novas metodologias facilitadoras da aprendizagem, possibilitando uma maior participação desses alunos.

Para que possamos pensar nessa aprendizagem significativa, descrita por Ausubel, precisamos ampliar e reconfigurar as formas que existem de descobrir para aprender, bem como considerar sempre o que nossos alunos trazem consigo, pois eles nunca vêm vazios. Devemos incentivá-los a criarem teses verdadeiras ou falsas. Esse conhecimento trazido por eles são os chamados “conhecimentos socialmente estruturados”, por isso, para Ausubel, uma aula deve sempre começar por uma pergunta.

Descrevendo a metodologia

Este trabalho pretende investigar a importância da Matemática para os futuros pedagogos como forma de contribuir, por bases metodológicas, à tecnologia digital no trabalho dos futuros docentes, principalmente na resolução de problemas com números fracionários, tanto no conjunto dos números racionais como no dos irracionais. Para atingirmos o objetivo proposto desta pesquisa, a metodologia utilizada é a exploratória. Faremos por meio de uma Capacitação trabalhada no processo. Para deixar claro para o leitor quanto às características metodológicas deste trabalho, mostraremos abaixo como se dará a análise dos dados coletados.

Tipo de pesquisa:	Descritiva/Exploratória
Natureza da pesquisa:	Qualitativa/Quantitativa
Estratégia da pesquisa:	Capacitação/Questionário
Técnica de coleta de dados:	Estudo de caso/Situação problema
Técnica da análise de dados:	Descritiva e análise de conteúdo

Esta capacitação foi realizada com dezenove alunos e alunas do curso de Pedagogia na instituição de ensino onde atuamos com Matemática e Estatística. Para iniciarmos a capacitação, construímos uma sequência didática (SD), descrevendo cada passo do trabalho, por meio de atividades digitais e atividades concretas. Em um segundo momento, solicitamos que cada participante escrevesse um pequeno texto sobre o que achavam da Matemática. Foram apresentadas diferentes situações e diferentes escritas sobre suas dificuldades e temores. Com uma distribuição de frequência, mostramos em um quadro geral como foram as falas dos alunos e das alunas sobre a qualidade do ensino.

Percepção do aluno	Número de alunos	Porcentagem
Medo	9	19
Raciocínio lógico	6	13
Fundamental	10	22
Lúdico	4	9
Cotidiano	11	24
Desmistificar	6	13
Total	46	100

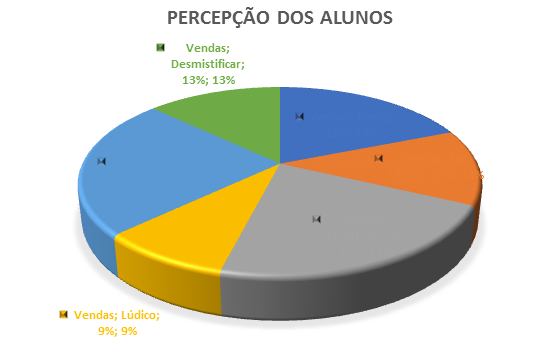
O que procuramos neste trabalho foi a importância da tecnologia digital para os novos saberes dos alunos, buscando alternativas facilitadoras e viáveis de uma aplicação metodológica inovadora ao ensino da Matemática.

Organização do trabalho

A organização do trabalho teve como público-alvo os alunos de uma instituição de ensino superior do curso de Pedagogia, principalmente alunos dos períodos finais, pois eles já teriam cursado as disciplinas de Metodologias da Matemática das Séries Iniciais e Finais e de Estatística Aplicada à Educação. Em um primeiro momento, desenvolvemos na disciplina de Metodologia, uma Sequência Didática, visando à Capacitação dos estudantes do período. Foram realizados 5 encontros, com 2 horas diárias, divididos em fases:

1. Solicitamos que escrevessem um pequeno texto de como percebiam o ensino da Matemática, a fim de conhecermos individualmente cada um e as suas angústias em relação ao aprendizado matemático;
2. Apresentamos a sequência didática que desenvolvemos nas aulas de Metodologia;
3. Destacamos a importância das tecnologias digitais como metodologia facilitadora dessa aprendizagem matemática e desenvolvemos todas as atividades em ambiente virtual de aprendizagem (AVA); destacamos os seguintes softwares educacionais: Canva, Learning Apps, WordWall, Liveworksheets, PowerPoint, Prezi.
4. Desenvolvemos jogos digitais para que os alunos os aplicassem como novos saberes à tecnologia, tais como:
   https://learningapps.org/view18783023
   https://learningapps.org/view20202620
   https://learningapps.org/view17162765
   https://learningapps.org/view24115649
   https://learningapps.org/view11239604
   https://learningapps.org/view21449126
   https://learningapps.org/view20822540
   https://learningapps.org/view16814495
   https://learningapps.org/view24544075
   https://learningapps.org/view24265181
   https://learningapps.org/view11425786
5. Permitimos, ao final da capacitação, que cada participante avaliasse o novo processo de ensino construído por meio da tecnologia digital, assim como o processo tradicional sobre o qual foram ensinados.

Considerações finais

Entendemos que para a concretização exitosa do nosso trabalho foi necessária uma mudança de concepção por parte dos futuros professores do curso de Pedagogia. Pensamos no uso de situações inovadoras com a tecnologia digital e as metodologias ativas no sentido de conscientizar os futuros profissionais da Educação da necessidade de inserir em suas atividades acadêmicas processos que possibilitem uma aprendizagem prazerosa e significativa, que os aproxime dos discentes. Assim, o professor deve pensar, constantemente, em formas investigativas de desenvolvimento da sua prática no ensino da Matemática.

Precisamos, urgentemente, levar em consideração não somente os aspectos conceituais e os axiomas matemáticos, mas também os conceitos sociais e culturais a partir dos quais desenvolvemos essa aprendizagem. Com isso, podemos dar mais sentido aos novos saberes, para que aconteçam de forma concomitante aos saberes trazidos das crianças à sala de aula.

Podemos concluir que, antes de modificar qualquer prática, devemos buscar novos projetos e novas concepções acerca do que é ensinar Matemática, mudando a nossa concepção também do que é aprendê-la. Nesse sentido, um dos caminhos mais curtos e mais sensíveis seria por meio do uso das Tecnologias Digitais, principalmente com atividades lúdicas que potencializam o processo investigativo, possibilitando ao nosso alunado pesquisar e descobrir novos sentidos de se aprender a Matemática. Esse novo processo deve ser apresentado logo na formação inicial do professor de Matemática com a intencionalidade voltada à mudança de postura do professor, fazendo com que entenda que as práticas investigativas de qualidade podem ser alcançadas junto às novas tecnologias, com os diferentes softwares educacionais já disponíveis no mercado.

Referências

ALMEIDA, M. E. B. Tecnologias digitais na Educação: o futuro é hoje. In: 5º ENCONTRO DE EDUCAÇÃO E TECNOLOGIA DE INFORMAÇÃO E COMUNICAÇÃO. Rio de Janeiro, 2007.

D’AMBROSIO, U. Da realidade à ação: reflexões sobre Educação Matemática. Campinas: Summus, 1986.

D’AMBROSIO, U.; STEFFE, Beatriz S. O ensino construtivista: tendências na Educação Matemática. MEC, Brasília, ano 14, n° 62, abr./jun. 1994.

EVES, Howard. Introdução à História da Matemática. Campinas: Editora da Unicamp, 2004.

FIORENTINI, D. L. S. Investigação em Educação Matemática: percursos teóricos e metodológicos. 3ª ed. Campinas: Autores Associados, 2009.

GAZIRE, E. S. O. Não Resgate da Álgebra. Tese (Doutorado em Educação Matemática) - Universidade Estadual de Campinas, Campinas, 2000. Disponível em: http://www.bibliotecadigital.unicamp.br/document/?code=vtls000218945. Acesso em: 5 maio 2014.

GRAVINA, M. A.; SANTAROSA, L. M. A aprendizagem de Matemática em ambientes informatizados. In: IV CONGRESSO RIBIE. Anais... Brasília, 1998. Disponível em: http://www.miniweb.com.br/ciencias/artigos/aprendizagem_mat.pdf. Acesso em: 7 maio 2014.

LEITE, L. S. Tecnologia educacional: descubra suas possibilidades na sala de aula. 2ª ed. Petrópolis: Vozes, 2004.

MORAN, J. M.; MASETTO, M. T.; BEHRENS, M. A. Novas tecnologias e mediações pedagógicas. 8ª ed. São Paulo: Papirus, 2013.

MOREIRA, M. A.; MASINE, E. A. F. S. Aprendizagem significativa: a teoria de David Ausubel. São Paulo: Moraes, 1982.

PAPERT, S. Logo: computadores e educação. 3ª ed. São Paulo: Brasiliense, 1988.

VALENTE, J. A. O computador na sociedade do conhecimento. Campinas: NIED/Unicamp, 2002.