Função quadrática: uma análise da aprendizagem em tempos de pandemia numa escola pública do Distrito Federal
Diego Wilson da Silva Neres
Licenciado em Matemática, mestrando (Profmat/UnB)
Wescley Well Vicente Bezerra
Doutor em Educação, professor da UnB e do Profmat/UnB
Tatiane da Silva Evangelista
Doutora em Matemática, professora da UnB e do Profmat/UnB
Os anos de 2020 e 2021 foram atípicos, em especial para os jovens em idade escolar, por conta da pandemia da covid-19. Nesse período, ocorreu uma mudança súbita de regime de estudo, de presencial para remoto, sem ter havido qualquer possível transição. A pandemia mudou a forma como os conteúdos foram desenvolvidos, em especial no Brasil. Em diferentes regiões do país, ocorreu um período inicial de suspensão das aulas presenciais e, posteriormente, instituiu-se uma tentativa de adaptação a um regime de estudo não presencial. Além disso, foi necessário ajustar o ensino remoto para a maioria da população, pois existe uma variedade de realidades socioeconômicas que deve ser levada em conta na forma de desenvolver o conteúdo com os estudantes.
No Distrito Federal, no ano de 2020, o ensino público foi suspenso em março e ficou assim por três meses, tendo retornado no final de junho. Durante esse período, algumas escolas tentaram manter alguma atividade escolar, ainda que de maneira informal. No fim de junho daquele ano, ocorreu o retorno das atividades escolares de maneira formal, na modalidade de ensino remoto, por meio da plataforma G-Suite, do Google (atualmente chamada de Google Workspace); o encerramento do ano letivo ocorreu em janeiro de 2021.
Na ocasião, cada escola pública teve autonomia para determinar de que modo seriam desenvolvidas suas atividades, que poderiam ir de publicações de textos de apoio a videoaulas, em tempo real ou gravadas pelos professores, passando por vídeos disponíveis no YouTube. É importante frisar que atividades impressas seriam disponibilizadas aos estudantes sem acesso à plataforma, havendo a necessidade de ir buscá-las em suas respectivas escolas, semanal ou quinzenalmente.
O ensino remoto permaneceu na Secretaria de Estado de Educação do Distrito Federal (SEEDF) até o final do segundo bimestre de 2021, tendo-se iniciado o ensino híbrido em agosto, após a vacinação das categorias de professores e demais funcionários das escolas. Nessa modalidade de ensino, em uma semana, metade dos alunos das turmas assistiam às aulas presencialmente, enquanto a outra metade permanecia com atividades remotas impressas ou pela plataforma do Google. Já na semana seguinte, os grupos de alunos alternavam-se, tendo esse regime durado até o final de outubro. Em novembro, as aulas presenciais foram retomadas, mas alguns alunos, por questões relacionadas à saúde, ainda permaneceram remotamente até o fim do ano letivo.
Diante desse cenário tão atípico, é preciso observar se as mudanças para os regimes remoto e híbrido de ensino causaram perdas acadêmicas aos estudantes. Assim, é necessário desenvolver e consultar pesquisas que visem compreender o impacto da pandemia no contexto escolar, para o encaminhamento de possíveis soluções.
Objetivos gerais
Este trabalho tem por objetivo fornecer um panorama da situação de aprendizagem de estudantes de uma escola pública do Ensino Médio do Distrito Federal, com relação ao conteúdo de função quadrática, durante o período de ensino híbrido imposto pela pandemia da covid-19.
Função quadrática
A função quadrática é um conteúdo matemático muito importante, que deve ser trabalhado nos anos finais do Ensino Fundamental e no Ensino Médio, com aplicação em diferentes áreas, tais como a Física, a Química, a Biologia etc. Além disso, a construção e a análise de gráficos são práticas que podem auxiliar os estudantes no exercício de sua cidadania.
No mundo das informações no qual estamos inseridos, torna-se cada vez mais precoce o acesso do cidadão a questões sociais e econômicas em que tabelas e gráficos sintetizam levantamentos, e índices são comparados e analisados para defender ideias. Dessa forma, faz-se necessário que a escola proporcione ao estudante a formação de conceitos que o auxiliem no exercício de sua cidadania e o torne protagonista de sua aprendizagem e de transformações sociais (Distrito Federal, 2020, p. 73).
Dada a importância desse tema de aprendizagem, o Currículo em movimento do Novo Ensino Médio do Distrito Federal traz alguns objetivos de aprendizagem específicos para as funções quadráticas:
MAT09FG Estruturar, gráfica e algebricamente, situações-problema de função polinomial do 2º grau, relacionando números expressos em tabelas e sua representação no plano cartesiano, para identificar padrões e criar conjecturas.
MAT10FG Delinear correspondência entre modelos algébricos e plano cartesiano ao elaborar gráficos de funções polinomiais de 2° grau. Por exemplo, em situações de lançamento oblíquo de objetos.
MAT11FG Estruturar, gráfica e algebricamente, situações-problema por meio de funções polinomiais de 1º e 2º graus, para a construção de modelos, visando a resolução de problemas em contextos diversos, com ou sem o apoio de tecnologias digitais.
MAT12FG Investigar pontos de máximo ou de mínimo de funções quadráticas em contextos envolvendo superfícies, Matemática Financeira ou Cinemática, entre outros, com ou sem apoio de tecnologias digitais (Distrito Federal, 2020, p. 74).
Além disso, a Base Nacional Comum Curricular (BNCC) também destaca algumas habilidades relacionadas ao tema de funções quadráticas, ressaltando sua importância:
(EM13MAT502) Investigar relações entre números expressos em tabelas para representá-los no plano cartesiano, identificando padrões e criando conjecturas para generalizar e expressar algebricamente essa generalização, reconhecendo quando essa representação é de função polinomial de 2º grau do tipo y = ax2.
(EM13MAT503) Investigar pontos de máximo ou de mínimo de funções quadráticas em contextos envolvendo superfícies, Matemática Financeira ou Cinemática, entre outros, com apoio de tecnologias digitais (Brasil, 2018, p. 541).
Antes de ser desenvolvido no Ensino Médio, o conteúdo de função quadrática é estudado no 9º ano do Ensino Fundamental, de acordo com o Currículo em movimento do Distrito Federal – Ensino Fundamental: anos iniciais – anos finais. Nessa etapa escolar, segundo tal documento, espera-se que o aluno saiba definir, identificar e representar geométrica e algebricamente as funções do 2º grau. Elas têm como objetivos de aprendizagem:
compreender as funções como relações de dependência unívoca entre duas variáveis e suas representações numérica, algébrica e gráfica.
Estruturar gráfica e algebricamente situações-problema por meio de funções de 1º e 2º graus, relacionando duas grandezas por meio de relação biunívoca existentes entre os elementos que as compõem, visando resolução de problemas, análise de conjecturas e tomada de decisões (Distrito Federal, 2018, p. 200).
Na seção “Matemática e suas tecnologias no Ensino Médio”, da BNCC, na terceira competência específica – que se refere a quais habilidades devem ser desenvolvidas em relação ao conteúdo da função polinomial do 1º e 2º graus –, estão presentes a interpretação e construção de modelos, a resolução e formulação de problemas matemáticos, bem como a aplicação de conceitos matemáticos e a construção de significados para eles. De acordo com o Currículo em movimento do Novo Ensino Médio, o conteúdo de funções polinomiais do 1º e 2º graus é novamente estudado e aprofundado no 1º ano desse segmento. É importante observar que o livro-texto adotado na escola em que esta pesquisa foi desenvolvida está de acordo com a BNCC, com o currículo do Ensino Médiodo DF e com os objetivos contidos no Currículo em movimento do Novo Ensino Médio.
Metodologia
Para esta investigação, o primeiro autor deste artigo, Diego Neres, criou um formulário na plataforma G-Suite, do Google – que, conforme já mencionado, a SEEDF utilizou como ambiente virtual de interação escolar. Esse formulário foi respondido por 171 estudantes do Ensino Médio, dos 1º, 2º e 3º anos, de uma escola pública do Distrito Federal, no período de 7 a 26 de outubro de 2021.
O formulário possuía três seções e deveria ser respondido de forma anônima pelos estudantes. As seções eram: “Sobre o desenvolvimento do conteúdo”, com seis perguntas; “Sobre a parte gráfica”, com onze perguntas, e “Sobre a parte do cálculo”, com sete perguntas.
Questões do tipo: “Você já estudou o conteúdo de funções quadráticas na escola?” e “Você viu o conteúdo em qual modalidade de ensino?” faziam parte da seção “Sobre o desenvolvimento do conteúdo”. Já na seção “Sobre a parte gráfica”, algumas perguntas eram: “Marque qual é o formato do gráfico da função quadrática” e “As raízes da função quadrática nos indicam…”. Por fim, na seção “Sobre a parte do cálculo”, algumas das perguntas presentes foram: “Para a função quadrática dada abaixo, marque a opção que corresponde às coordenadas do vértice da função…” e “Para a função quadrática dada abaixo, marque a opção que corresponde às raízes da função, utilizando a fórmula resolutiva da função do 2º grau (fórmula de Bhaskara)”.
A pesquisa seguiu uma abordagem qualitativa, que, segundo Creswell, é um
processo de pesquisa [que] envolve as questões e os procedimentos que emergem, os dados tipicamente coletados no ambiente do participante, a análise dos dados indutivamente construída […] e as interpretações feitas pelo pesquisador acerca do significado dos dados (Creswell, 2010, p. 26 , adendo nosso).
Resultados e discussões
Dos 171 estudantes pesquisados, um estudava no 1º ano (0,6%), 21 estudavam no 2º ano (12,3%) e 149 estudavam no 3º ano (87,1%). Quando perguntados se já haviam estudado o conteúdo de funções quadráticas na escola, 11 estudantes disseram que não (6,4%) e 160 disseram que sim (93,6%).
Ao serem questionados em qual modalidade de ensino tinham visto o conteúdo, 51 estudantes responderam “apenas presencial” (29,8%), 31 responderam “apenas remoto” (18,1%) e 89 responderam “remoto e presencial” (52%).
Com relação ao questionamento sobre se o professor tinha podido desenvolver o conteúdo em tempo adequado, 69 disseram que sim (40,4%), 27 disseram que não (15,8%) e 75 não souberam opinar (43,9%).
Perguntados se o professor conseguira desenvolver os principais pontos do conteúdo, 70 responderam “sim, completamente” (40,9%), 41 responderam “não, teve pouco tempo” (24%) e 70 responderam “apenas parcialmente” (35,1%).
Em relação à questão sobre se o estudante considerava que as aulas remotas tinham sido produtivas durante o período totalmente online, 18 responderam que sim (10,5%), 69 responderam que não (40,4 %) e 84 responderam que parcialmente (49,1%).
Portanto, nota-se que, como a maioria dos estudantes estava cursando o 3º ano do Ensino Médio, muitos já haviam estudado o conteúdo em questão. Como apenas 18,1% disseram que o haviam estudado apenas na modalidade remota e 29,8% relataram terem estudado função quadrática apenas no presencial, podemos inferir que o conteúdo foi ministrado nos 1º e 2º anos, podendo ter sido revisado no 3º ano. Também se observa que os percentuais de estudantes que declararam que o professor pôde desenvolver o conteúdo em tempo adequado e que ele conseguiu abordar os principais pontos do conteúdo ficaram bastante próximos, o que revela a coerência dos dados coletados. Outro fato importante é que a maioria dos estudantes não considerou as aulas remotas produtivas ou a considerou penas parcialmente produtivas.
Com relação à parte gráfica, a primeira pergunta pedia para que os estudantes marcassem qual era a forma reduzida da função quadrática. A primeira opção era a forma reduzida da função afim; a segunda, a da função quadrática e a terceira, a da função do 3º grau. Segundo as respostas obtidas, aproximadamente dois terços dos estudantes conseguiram identificar corretamente a função quadrática.
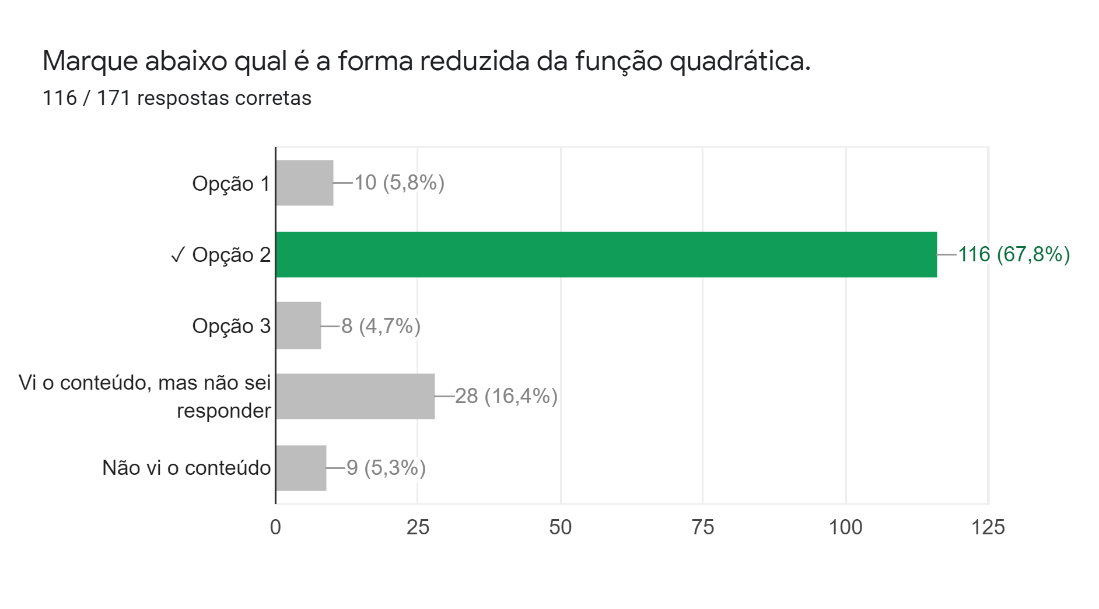
Figura 1: Primeira pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na segunda pergunta, foi pedido para que os alunos marcassem qual era o formato do gráfico da função quadrática. A primeira opção era o gráfico de uma função do 3º grau; a segunda, o de uma função afim e a terceira, o gráfico da função quadrática, todas passando pela origem. Os resultados mostraram que aproximadamente três quartos dos estudantes conseguiram identificar visualmente o gráfico da função quadrática.
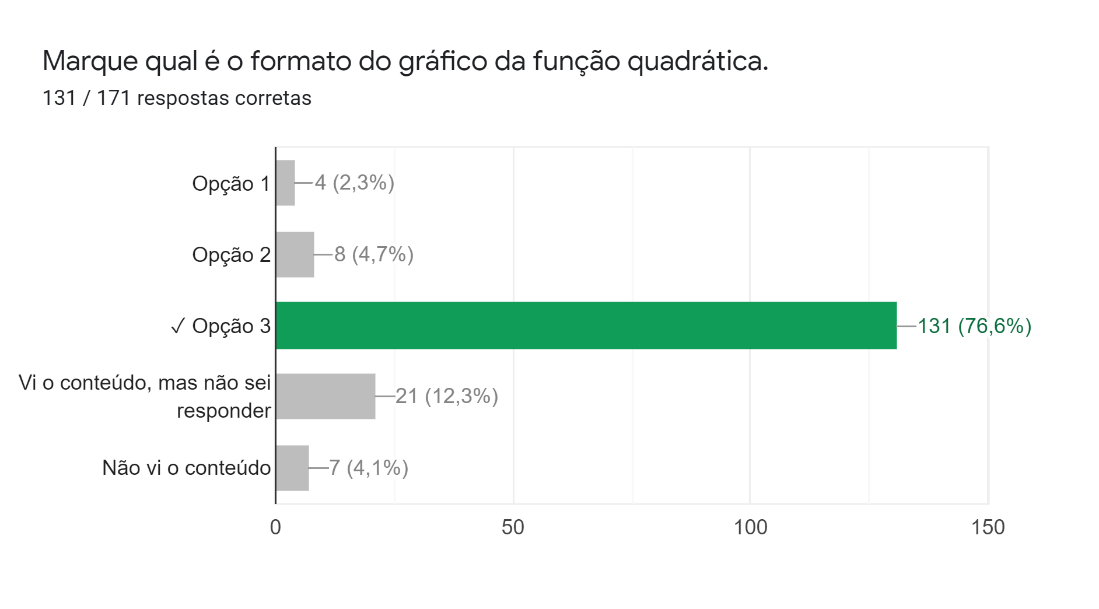
Figura 2: Segunda pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na terceira pergunta, o pedido era para que os alunos indicassem o nome do gráfico da função quadrática. Pelo percentual de respostas da Figura 3, percebe-se que aproximadamente três quartos dos estudantes foram capazes de identificar a opção correta.
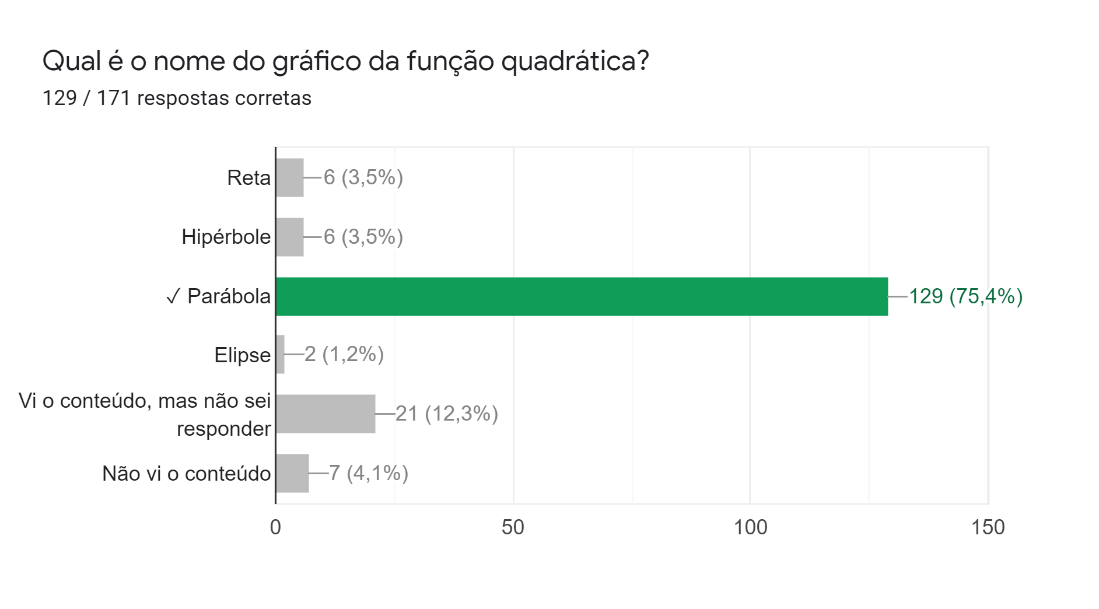
Figura 3: Terceira pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
A quarta pergunta pedia para que o eixo de simetria do gráfico da função quadrática fosse identificado. As respostas (Figura 4) revelam uma dificuldade nessa identificação, com apenas pouco mais da metade dos alunos tendo acertado e um quarto deles, aproximadamente, não tendo sabido responder.
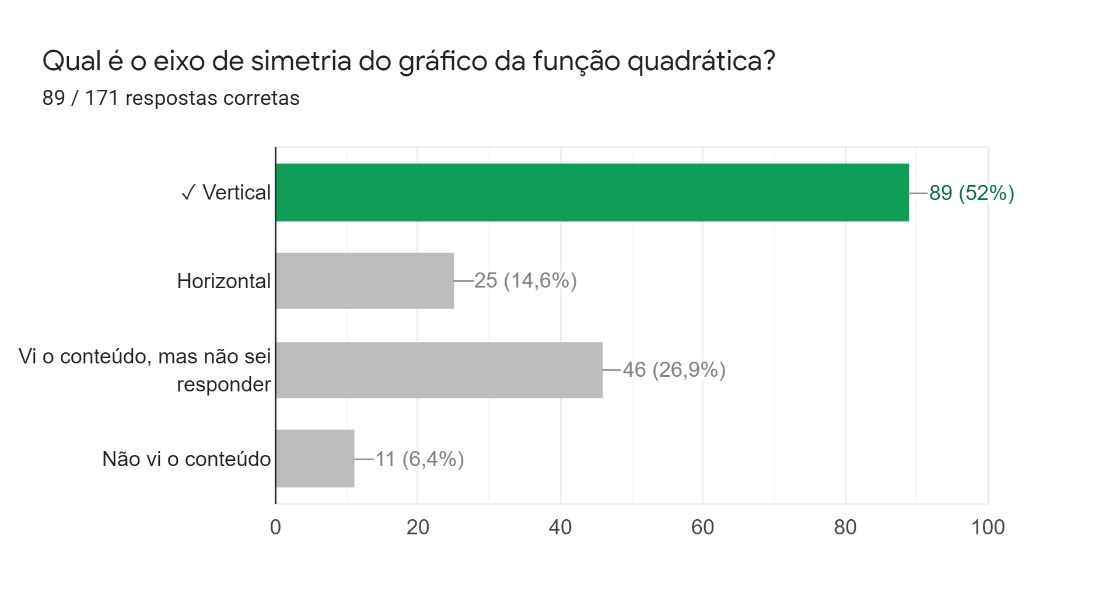
Figura 4: Quarta pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na quinta pergunta, os alunos foram questionados sobre a concavidade do gráfico, quando ela é voltada para cima com relação ao valor do coeficiente . Na questão, foi a primeira opção e foi a segunda. As respostas (Figura 5) mostram que pouco mais da metade dos estudantes identificou corretamente qual deve ser o valor do coeficiente para que a concavidade seja voltada para cima e quase um terço não soube responder, mesmo tendo visto o conteúdo.
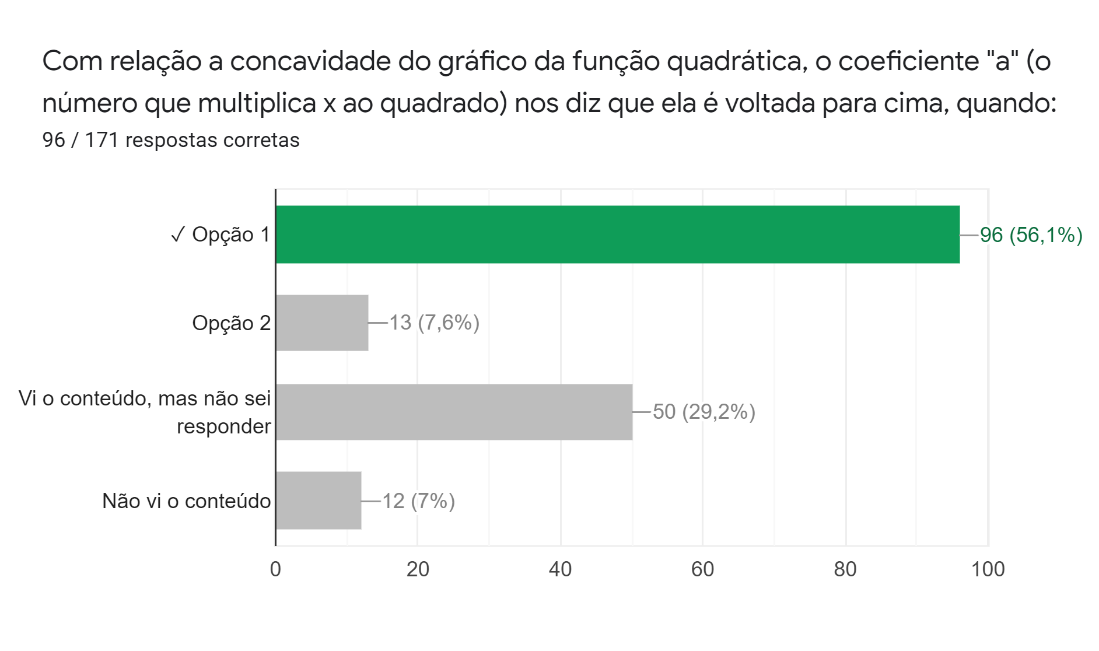
Figura 5: Quinta pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na sexta pergunta, os estudantes foram questionados sobre a concavidade do gráfico, quando ela é voltada para baixo com relação ao valor do coeficiente . Nela, a primeira opção foi e a segunda, . As respostas (Figura 6) nos indicam que pouco mais da metade do grupo identificou corretamente qual deve ser o valor do coeficiente para que a concavidade seja voltada para baixo e pouco menos de um terço deles não soube responder, mesmo tendo visto o conteúdo. Ressalta-se a compatibilidade dos valores em relação à pergunta anterior.
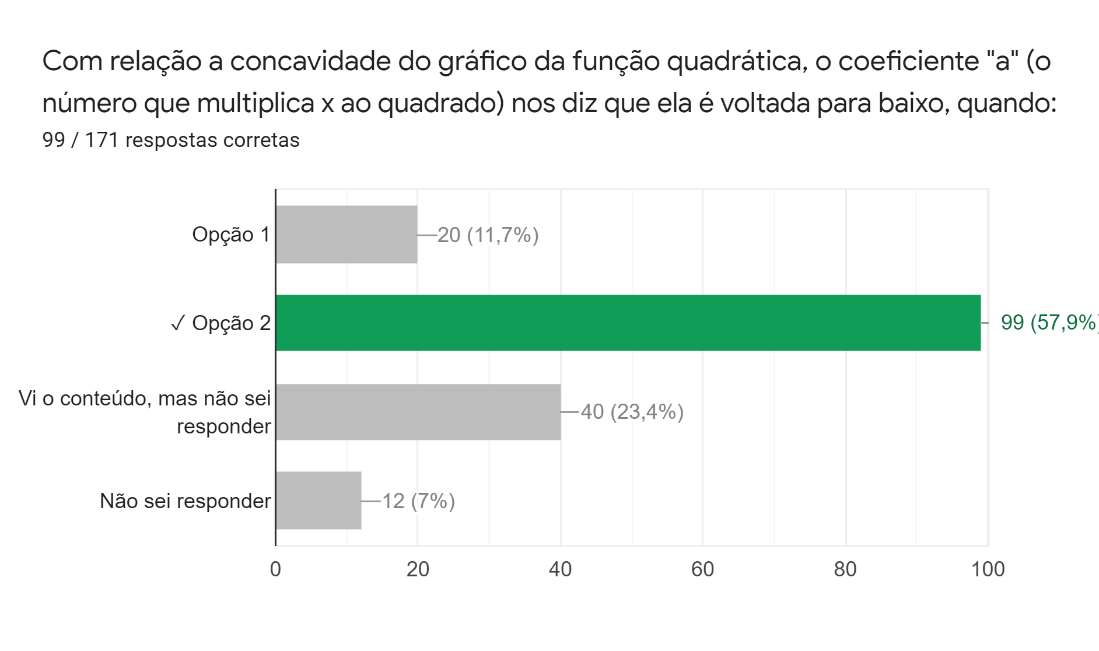
Figura 6: Sexta pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
A sétima pergunta pedia para que os alunos identificassem o que o coeficiente indicava. As respostas (Figura 7) nos mostram que metade dos estudantes soube responder corretamente, enquanto quase um terço não o soube, mesmo já tendo visto esse conteúdo.
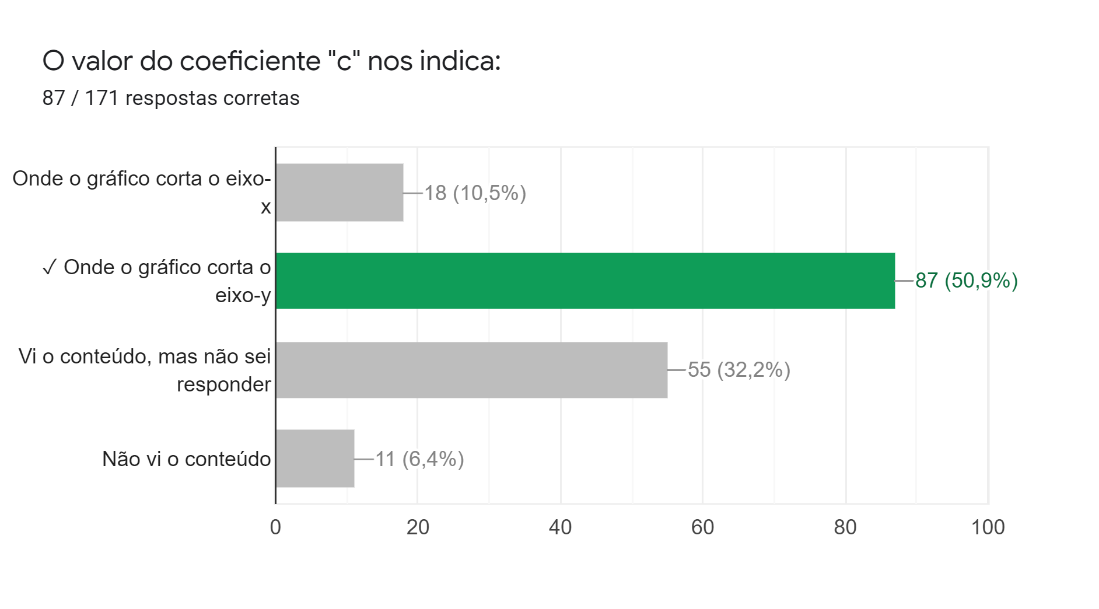
Figura 7: Sétima pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na oitava pergunta, foi pedida a identificação de qual tipo de translação horizontal o coeficiente indica. As respostas (Figura 8) mostram que poucos estudantes souberam responder corretamente e que mais de 40% não souberam responder, mesmo tendo visto o conteúdo.
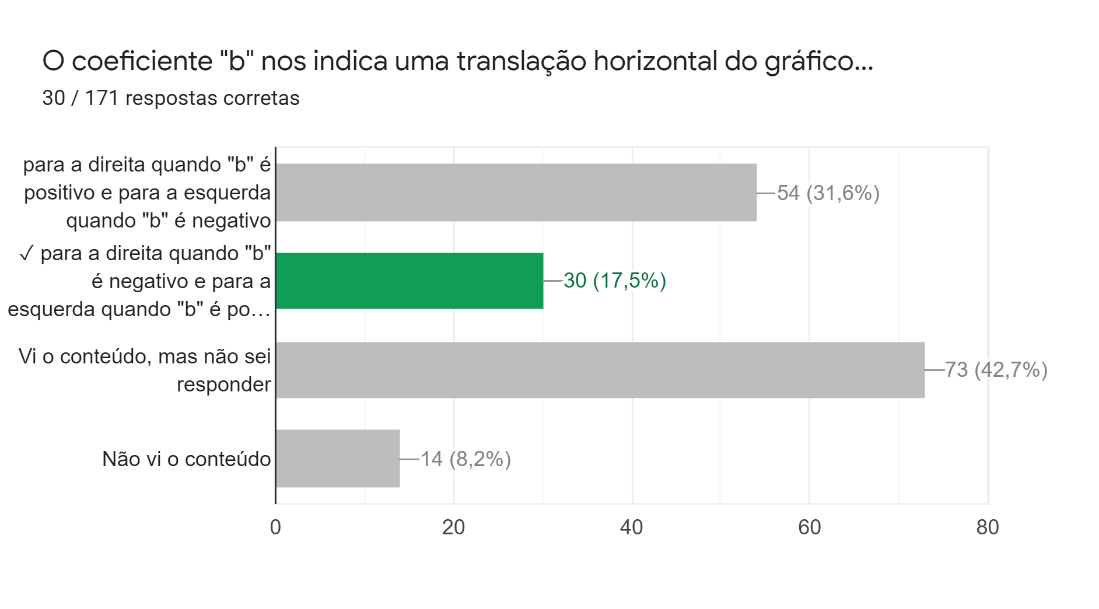
Figura 8: Oitava pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
A nona pergunta solicitava que os estudantes identificassem o que as raízes da função quadrática indicam. As respostas (Figura 9) nos mostram que praticamente metade dos estudantes soube responder corretamente e que pouco menos de 30% deles não foram capazes de responder, mesmo tendo visto o conteúdo.
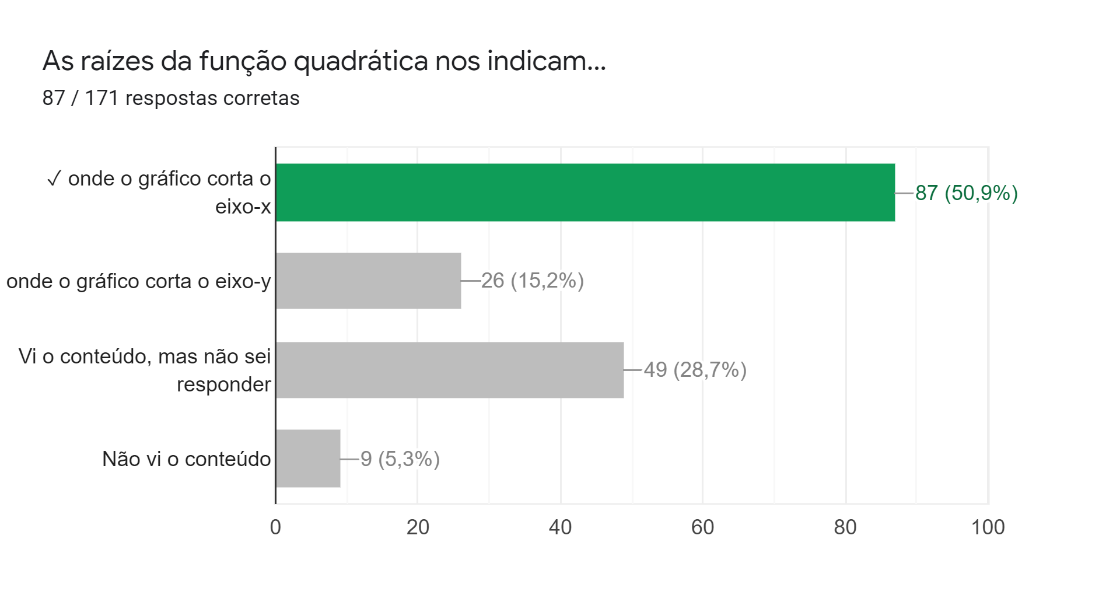
Figura 9: Nona pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na décima pergunta, pediu-se aos estudantes que marcassem a opção que exibia as relações corretas do discriminante delta com as raízes da função quadrática. As opções 1 e 2 eram, respectivamente:
Opção 1: |
Opção 2: |
∆ >0,possui duas raízes reais
|
∆ >0,não possui raízes reais ∆ =0,possui uma raíz real ∆ <0,possui duas raízes reais |
As respostas observadas na Figura 10 revelam que aproximadamente metade dos estudantes soube responder corretamente a essa questão, ao passo que um terço não soube, mesmo tendo visto o conteúdo.
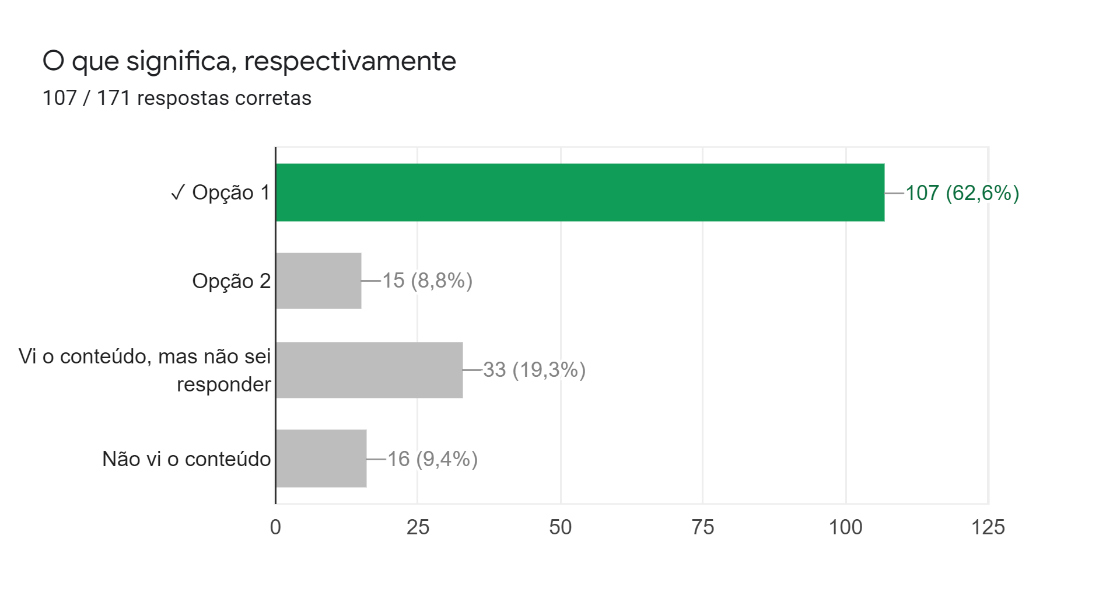
Figura 10: Décima pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Na décima primeira pergunta, foi pedido aos estudantes para que marcassem a opção que indicava o significado da linguagem simbólica das relações do discriminante delta: ∆ > 0,∆ = 0 e ∆ < 0, respectivamente. As opções 1 e 2 eram:
Opção 1: |
Opção 2: |
∆ ser positivo |
∆ ser negativo |
Por fim, a Figura 11 nos mostra que pouco menos de dois terços souberam responder corretamente e que pouco menos de 20% não souberam responder, mesmo tendo visto o conteúdo.
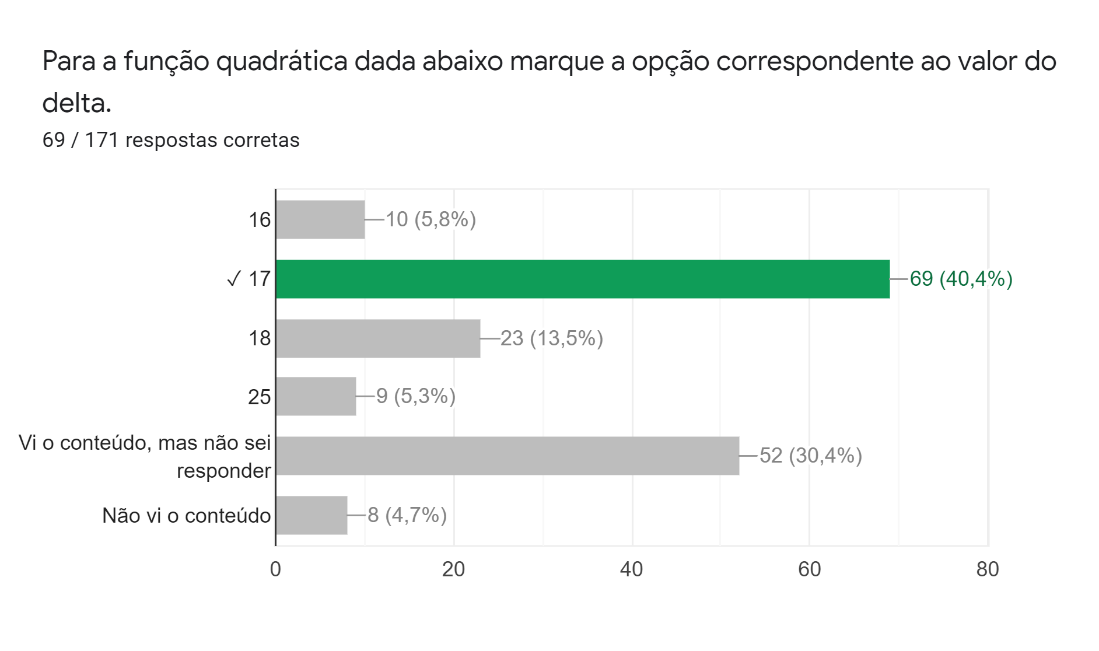
Figura 11: Décima primeira pergunta da parte gráfica
Fonte: Produzida por Diego Neres.
Com relação à parte dos cálculos, foram dadas algumas questões, relativas a partes distintas do conteúdo, para que fossem resolvidas, de modo que fosse possível avaliar a aprendizagem desses tópicos.
Na primeira questão, foi solicitou-se que os estudantes marcassem o valor da discriminante delta da função com a expressão do delta dado. As respostas (Figura 12) nos indicam que, aproximadamente, 40% assinalaram de maneira correta, ao passo que 30% não souberam responder, mesmo tendo visto o conteúdo.
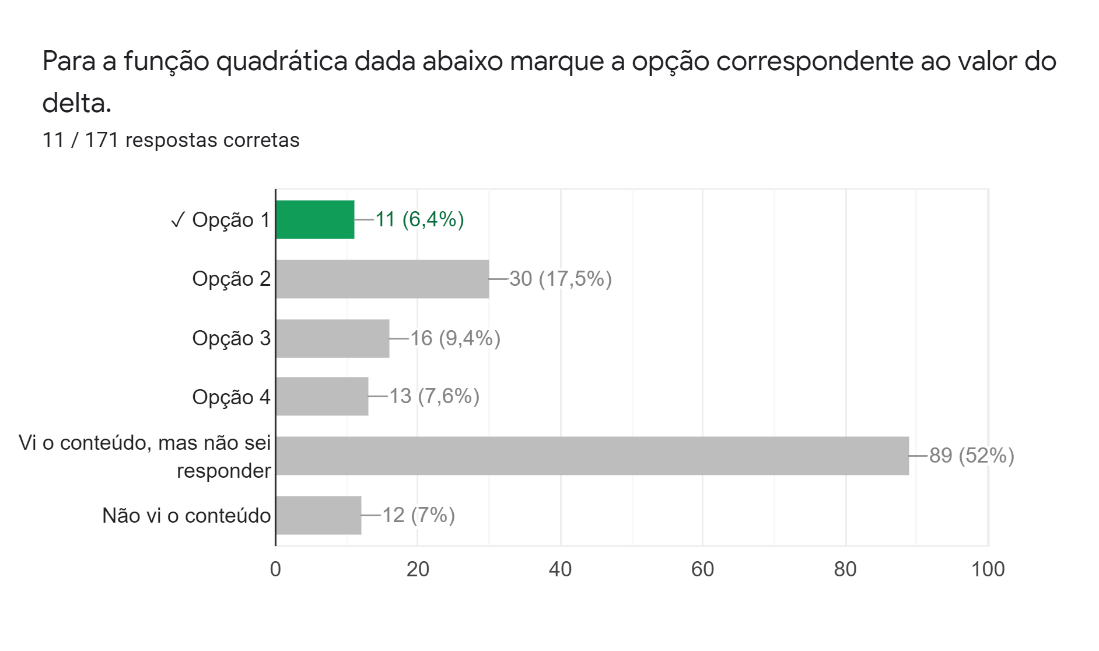
Figura 12: Primeira pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
A segunda questão da parte de cálculos pedia o mesmo que a primeira, mas, desta vez, com frações nos coeficientes e , para a função , com a expressão do delta dado. As respostas (Figura 13) indicam uma taxa de acerto muito pequena, de apenas 6,4%, enquanto 34,5% erraram a questão. A maioria (52%) não soube responder, mesmo tendo visto o conteúdo.

Figura 13: Segunda pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
Na terceira questão, os alunos deveriam encontrar as raízes da função , utilizando a regra da soma e do produto, com as respectivas fórmulas dadas. As respostas (Figura 14) mostram que apenas 25,7% marcaram corretamente a resposta – uma quantidade menor do que a dos que erraram, que somam 28% –, enquanto pouco mais de 36% não souberam responder, mesmo tendo visto o conteúdo.
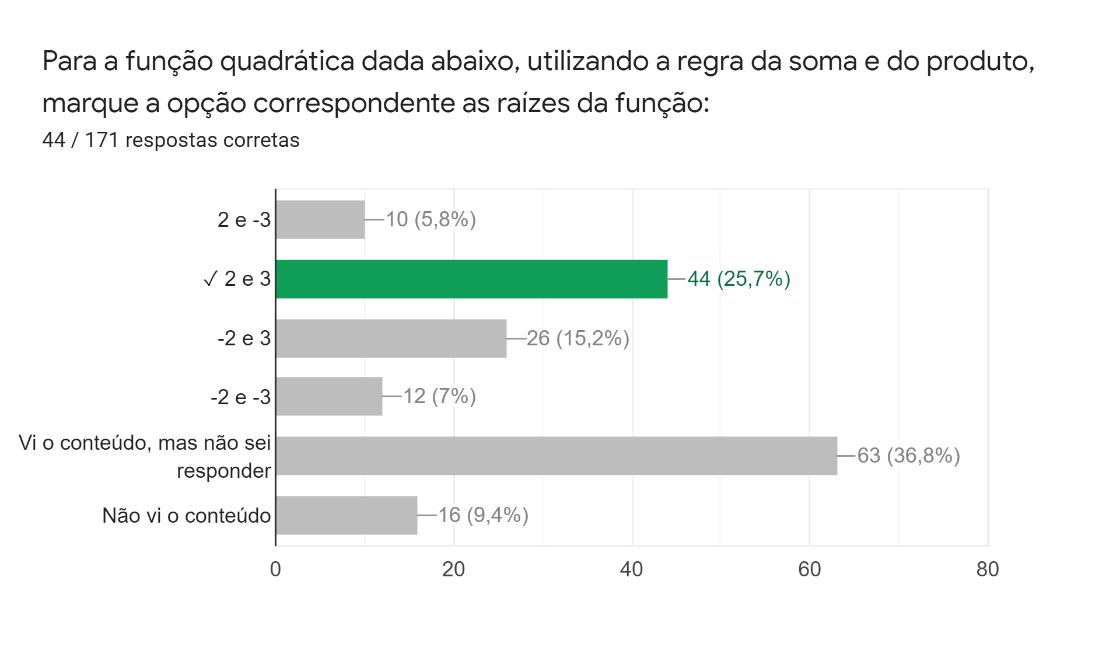
Figura 14: Terceira pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
Na quarta questão desta parte, foi pedido para que fossem encontradas as coordenadas do vértice da função , com as igualdades de e dadas. As respostas (Figura 15) indicam que 23,4% dos estudantes acertaram a questão, enquanto 19,9% a erraram. Também é possível observar que quase metade dos estudantes (47,4%) não soube responder, mesmo já tendo visto o conteúdo.
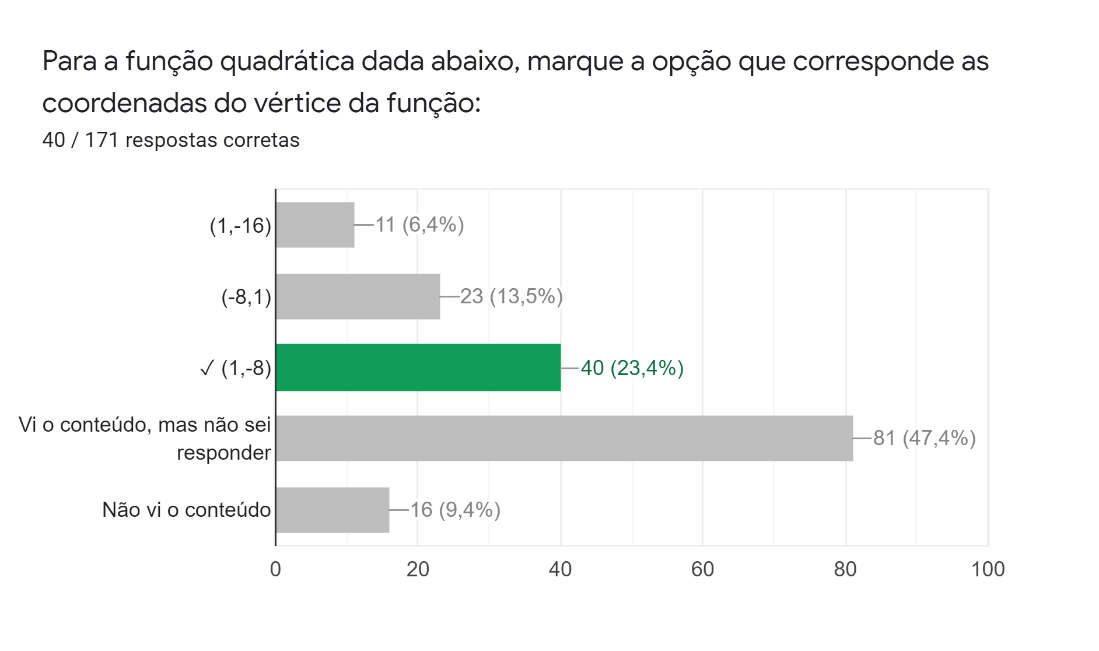
Figura 15: Quarta pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
Na quinta questão, solicitava-se encontrar as raízes da função , utilizando a fórmula resolutiva da função do 2º grau. As respostas dessa questão (Figura 16) mostram que 28,1% dos estudantes responderam corretamente, uma quantidade menor que a de erros – que somam 32,2%. Já cerca de 35,4% não souberam responder, mesmo tendo visto o conteúdo.
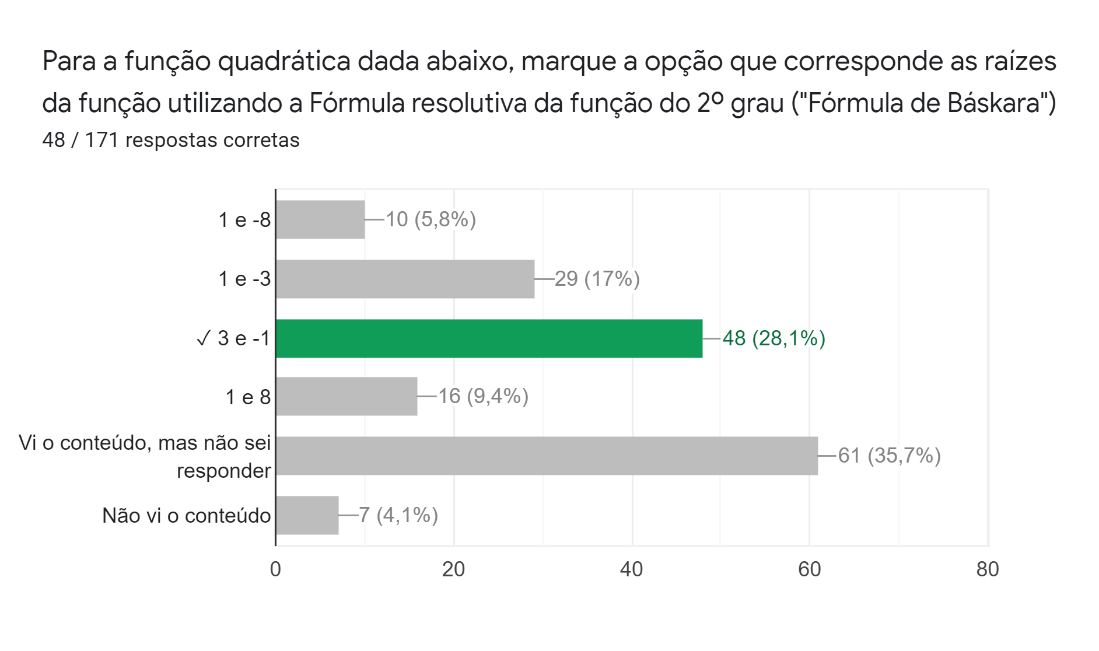
Figura 16: Quinta pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
Na sexta questão, foi pedido para marcar a opção da forma fatorada da função , com a fórmula da forma fatorada dada. As respostas (Figura 17) mostram que apenas 17,5% souberam responder corretamente à questão, enquanto 29,8% a erraram, valor pouco menor que os 42,1% que não souberam responder, mesmo tendo visto o conteúdo.
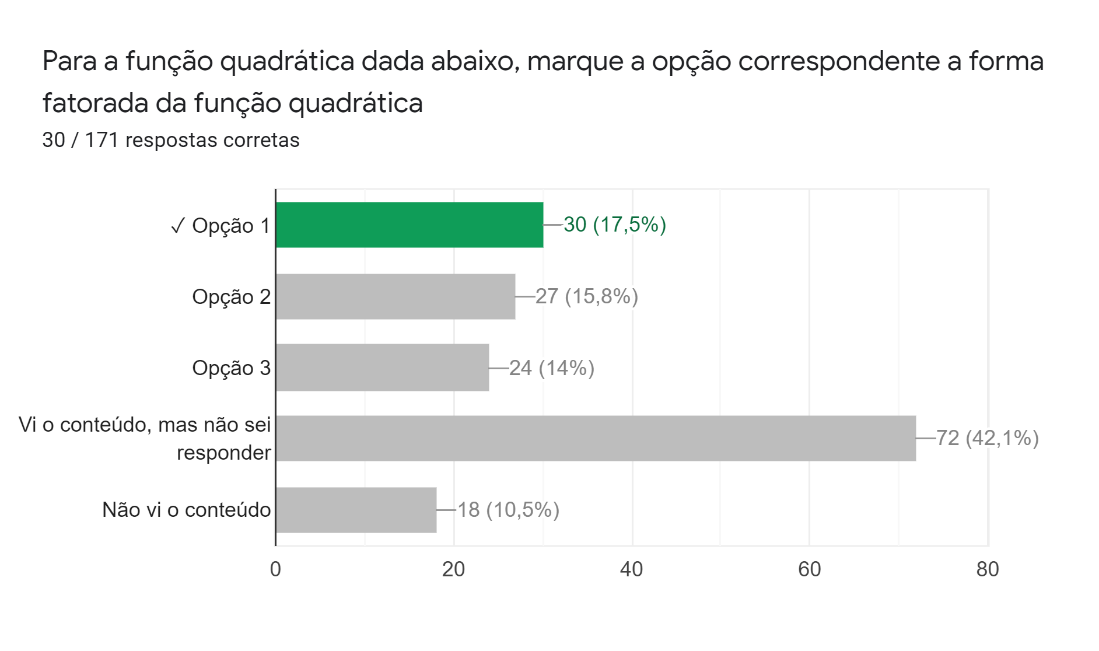
Figura 17: Sexta pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
Enfim, na sétima questão, da mesma forma que na quinta, pedia-se para que fossem encontradas as raízes da função , utilizando, para isso, a fórmula resolutiva da função do 2º grau. As respostas (Figura 18) indicam que 29,8% dos estudantes acertaram a questão, enquanto 32,8% a erraram e que 32,2% –um valor menor que o de erros – não souberam responder, mesmo tendo visto o conteúdo.
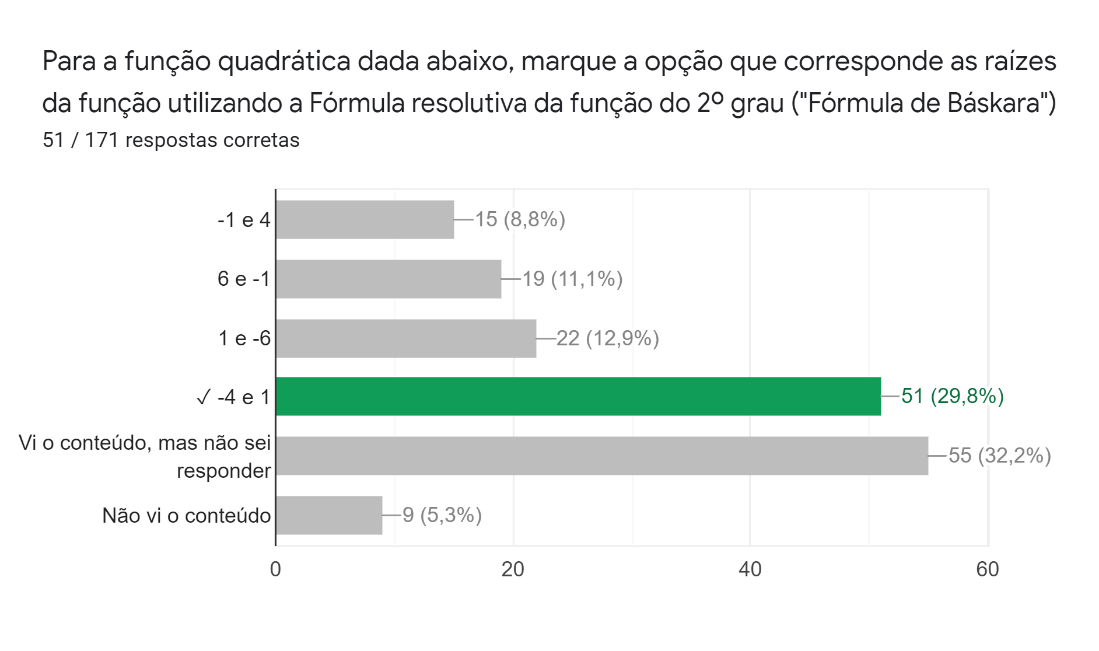
Figura 18: Sétima pergunta da parte de cálculo
Fonte: Produzida por Diego Neres.
A partir dessas respostas, foi possível observar algumas dificuldades, por parte dos estudantes, no desenvolvimento dos cálculos que envolvem o discriminante, principalmente quando os coeficientes são frações (dado o nível de acerto extremamente baixo (6,4%), com 52% afirmando que não saberiam resolver, mesmo que o conteúdo já tinha sido visto).
Nas questões em que os conteúdos eram: 1) a regra da soma e do produto para encontrar as raízes da função quadrática; 2) as coordenadas do vértice do gráfico; 3) encontrar a forma fatorada da função e 4) a utilização da fórmula resolutiva da função do 2º grau, a taxa de erro foi relativamente alta para cada questão. Além disso, para esses tópicos, a ocorrência de respostas do tipo “Vi o conteúdo, mas não sei responder” foi superior a 32%, o que indica uma grande quantidade de estudantes que ainda não entenderam essa parte do conteúdo.
Conclusão
A partir dessa investigação, pode-se concluir que uma parcela relativamente alta dos estudantes que participaram da pesquisa apresentou dificuldades em desenvolver cálculos relacionados ao conteúdo de função quadrática. Além disso, ficou evidente, pelas altas taxas seleção da alternativa: “Vi o conteúdo, mas não sei responder”, que o processo de ensino disponibilizado durante a pandemia não obteve êxito em favorecer a aprendizagem desses alunos, com relação a esse conteúdo, em específico.
Apesar de o desempenho apresentado pelos alunos ter sido um pouco mais satisfatório nas questões da parte gráfica, com resultados entre 49,7% e 76,6% de acerto (com exceção da indicação da translação horizontal do gráfico pelo coeficiente b, da função quadrática), de forma geral, os resultados não são animadores, uma vez que, para essas questões, o nível de exigência era inferior à parte dos cálculos.
Infelizmente, o momento de ensino imposto pela pandemia da covid-19 gerou alguns problemas de aprendizagem, que foram causados por diferentes fatores: alunos que não tiveram acesso a uma internet de boa qualidade para manter o ritmo dos estudos em casa; lares que careciam de espaço adequado para o estudo; pais que não podiam acompanhar seus filhos durante as aulas remotas; professores desprovidos de recursos materiais para prepararem boas aulas remotas etc. Essa diversidade de aspectos levou os estudantes a entenderem ter visto os conteúdos de função quadrática, mas o insucesso da aprendizagem fez com que boa parte deles não soubesse responder as questões.
Dessa forma, é importante que os gestores priorizem, para os próximos anos, mecanismos que auxiliem os professores e os alunos a diminuir os impactos negativos na aprendizagem do conteúdo de funções quadráticas. Assim, a escola poderá fornecer as condições adequadas para que os estudantes possam exercer plenamente a sua cidadania.
Referências
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018. Disponível em: BNCC_EI_EF_110518_versaofinal_site.pdf . Acesso em: 21 set. 2022.
CRESWELL, John W. Projeto de pesquisa: métodos qualitativo, quantitativo e misto. Tradução de Magda Lopes. 3 ª ed. Porto Alegre: Artmed, 2010.
DISTRITO FEDERAL. Secretaria de Educação. Currículo em movimento do Distrito Federal – Ensino Fundamental: anos iniciais – anos finais. 2. ed. Brasília, DF: SEEDF, 2018. Disponível em: Currículo-em-Movimento-Ens-fundamental_19dez18.pdf . Acesso em: 1 ago. 2023.
DISTRITO FEDERAL. Secretaria de Educação. Currículo em movimento do Novo Ensino Médio. Brasília, DF: SEEDF, 2020. Disponível em: Curriculo-em-Movimento-do-Novo-Ensino-Medio_fev21.pdf. Acesso em: 1 ago. 2023.
Publicado em 08 de agosto de 2023
Como citar este artigo (ABNT)
NERES, Diego Wilson da Silva; BEZERRA, Wescley Well Vicente; EVANGELISTA, Tatiane da Silva. Função quadrática: uma análise da aprendizagem em tempos de pandemia numa escola pública do Distrito Federal. Revista Educação Pública, Rio de Janeiro, v. 23, nº 30, 8 de agosto de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/29/funcao-quadratica-uma-analise-da-aprendizagem-em-tempos-de-pandemia-numa-escola-publica-do-distrito-federal
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

