Design Thinking na Educação: trabalhando com habilidades socioemocionais
Gisele de Oliveira Ribeiro Pereira
Mestranda em Novas Tecnologias na Educação
Alessandro Jatobá
Doutor em Engenharia de Produção (Coppe/UFRJ)
Paulo Vitor de Carvalho
Professor nos Programas de Pós-Graduação em Informática da UFRJ
Este documento traz a utilização do Design Thinking na Educação por meio de uma sequência didática para a criação de um laboratório de Matemática. Ao longo dessa criação foi possível observar, fazer uma pesquisa e constatar a utilização de algumas habilidades socioemocionais.
A sequência didática foi aplicada em uma disciplina eletiva da Escola Sesc de Ensino Médio, situada no Rio de Janeiro. Tal disciplina compõe o quadro do itinerário formativo de Matemática, de acordo com as diretrizes do Novo Ensino Médio.
A ideia da construção de um laboratório de Matemática foi escolhida para que fosse possível criar objetos de aprendizagem que auxiliassem no ensino-aprendizagem, contudo tais objetos deveriam ser produzidos pelos alunos para que eles colocassem em prática os seus conhecimentos, realizassem pesquisas e pudessem ser protagonistas.
Objetivos
O objetivo geral é promover a autonomia, a criatividade e o pensamento crítico dos jovens por meio da elaboração de uma unidade curricular eletiva para o itinerário formativo de Matemática, e como consequência montar um Laboratório de Matemática. O laboratório deverá conter objetos concretos que facilitem o ensino e reforcem a aprendizagem nos segmentos da educação básica.
Para alcançar o proposto objetivo geral, faz-se necessário trilhar os seguintes passos ou objetivos específicos, como verificar a necessidade da criação de objetos de aprendizagens concretos para o ensino-aprendizado de determinados conteúdos e para quem ele se destina, modelar uma sequência didática fundamentada na metodologia do Design Thinking para viabilizar reflexão e aprendizagem criativa da Matemática para discentes do Ensino Médio e aplicar esta sequência didática, medindo e analisando seus resultados para a verificação da promoção das habilidades.
No referencial falaremos brevemente sobre as habilidades socioemocionais, o pensamento crítico em Matemática e o Design Thinking.
Habilidades socioemocionais
Dentre as teorias que versam sobre as competências socioemocionais, podemos citar como exemplo o Positive Psychology Program, Partners for 21st Century Skills e a proposta Colaborative for Academic, Social and Emotional Learning (Courtney; Ackerman, 2017). Essas teorias reforçam a ideia de que as competências socioemocionais formam um conjunto de habilidades que podem ser praticadas e treinadas, assim como a criatividade. Ou seja, tal habilidade que tem sido cada vez mais valorizada no mundo do trabalho, pode e deve ser aprimorada. Para a sala de aula, ela tem um valor inestimável aliada ao pensamento crítico. Resoluções diferenciadas surgem de mentes criativas que são capazes de entender o processo matemático, apresentando uma resposta bem fundamentada e trazendo uma importante riqueza para os debates em sala de aula.
O modelo Partnership for 21st Century Learning (Courtney; Ackerman, 2017), em defesa de uma educação sintonizada com as necessidades do atual momento, propõe que os sistemas educativos privilegiem no processo formativo dos estudantes o desenvolvimento de 6C: colaboration, communication, conectivity, culture, creativity and critical thinking (em livre tradução: colaboração, comunicação, conectividade, cultura, criatividade e pensamento crítico). Espera-se que os alunos trabalhem tais habilidades na disciplina eletiva Laboratório de Matemática.
Pensamento crítico em Matemática
O pensamento crítico (PC) é considerado habilidade essencial e um indicador da qualidade de ensino, porém não há um consenso sobre onde trabalhar as habilidades do pensamento crítico, se em cursos específicos para essa finalidade ou como parte integrante de algum outro curso. No entanto, professores de Matemática se deparam com essas e outras questões: ‘É possível incentivar o pensamento crítico?’ ‘É possível ensinar a pensar criticamente?’ ‘Como fazê-lo?’
Vamos tentar responder tais questões com base no artigo de Nada J. Alsaleh (2019), Teaching critical thinking skills: Literature review.
Pesquisadores discordam sobre as habilidades que tornam uma pessoa um pensador crítico, no entanto, parece evidente pela literatura de que há um consenso geral de que o PC inclui uma série de processos e habilidades mentais, como interpretação, análise, avaliação, inferência, explicação e autorregulação.
John Dewey (1933) observou que o pensamento crítico começa com um problema e termina com uma solução (e sua autointerpretação). Bean (2011) afirma que o problema deve “evocar a curiosidade natural dos alunos e estimular a aprendizagem e o pensamento crítico”. Kurfiss (1988, p. 2) definiu o PC como “uma investigação cujo propósito é explorar uma situação, fenômeno, questão ou problema para chegar a uma hipótese ou conclusão sobre ele que integre todas as informações e que pode, portanto, ser justificada de forma convincente”. Pithers e Soden (2000, p. 238) afirmaram que “o pensamento crítico deve ser capaz de identificar questões que valem a pena perseguir, [...] ser capaz de apresentar provas para apoiar os argumentos de alguém”. Ou seja, o PC pode ser encarado como a habilidade de encontrar uma solução adequada e lógica para um problema. É exatamente isso o que buscamos em Matemática.
Por que buscar o pensamento crítico? Conseguimos tecer várias conjecturas para tal pergunta, mas de maneira prática vamos nos ater ao fato de que ao não pensarmos de forma crítica, podemos tomar decisões erradas durante a resolução de um problema.
Ao refletir sobre o pensamento crítico podemos ter a ideia de alguém argumentando favoravelmente ou não sobre determinado assunto, fazendo sua análise crítica. Na Matemática não é diferente, pois o pensamento crítico se refere ao entendimento como um todo, mas não é como uma receita de bolo na resolução de um problema que pode variar conforme o contexto. De acordo com Firdaus e colaboradores (2015, p. 227), “os estudantes não devem apenas entender o conteúdo de Matemática, mas também o processo do pensamento matemático”. Para tal aprofundamento é importante o estudo, o interesse, a vontade de querer aprender. É comum vermos em sala de aula alunos que pedem “Professora, coloca só a fórmula”. Quando não há interesse em querer saber de onde vem uma equação ou uma demonstração, faz-se necessário provocar no aluno o interesse e a curiosidade, para que ao compreender o processo de demonstração, o educando, mesmo ao esquecer as fórmulas, possa ser capaz de desenvolver uma boa resolução por meio do raciocínio lógico, por ter uma compreensão maior sobre o assunto.
Design Thinking
A unidade curricular à qual se refere este trabalho foi planejada com o intuito de ser baseada no Design Thinking. O motivo de tal escolha é por acreditarmos que o método seja de fácil entendimento para educadores e educandos, além de ser algo moderno, considerado como metodologia ativa na área da educação e já ter sido consolidado nos mais diversos campos do mundo do trabalho.
A abordagem se destaca e é positiva para a educação por estar diretamente relacionada à empatia no que se refere à preocupação em criar algo que ajude o outro, por seu método investigativo e criativo, por requerer atuação direta de alunos e professores, por trazer um rápido retorno (se o produto alcançou seu objetivo ou não) e por trabalhar diversas habilidades relacionadas ao aspecto socioemocional.
A metodologia mencionada ganhou notoriedade com David Kelley, professor da Universidade de Stanford, fundador da consultoria de inovação IDEO, e seu colega Tim Brown, atual CEO da consultoria, embora ela tenha sido esboçada anteriormente por Herbert A. Simon (1969) no livro The science of the artificial.
Tim Brown (2010), autor do livro Uma metodologia poderosa para decretar o fim das velhas ideias - Design Thinking, cita a ênfase nas necessidades humanas, em oposição aos desejos efêmeros ou manipulados, orientando o Design Thinking a se distanciar do status quo.
Ao fazermos uma busca na internet de imagens sobre Design Thinking, nos deparamos com muitas imagens assim:

Figura 1: Infográfico do Design Thinking
Fonte: Atena Educacional, 2019.
A maioria dessas imagens traduz o método em 5 etapas ordenadas:
- Empatia - Verificar quem é o usuário e qual é o seu problema.
- Definir - Criar um ponto de vista baseado nas necessidades do usuário.
- Idear - Momento de incentivo às ideias. Pensar em soluções criativas possíveis.
- Prototipar - É a resposta de como mostrar suas ideias e criar suas representações.
- Provar - Compartilhar sua ideia prototipada. Testar o que funciona e o que não funciona.
Com tais etapas definidas, pensamos na sequência didática para o curso Laboratório de Matemática.
A seguir, trataremos do local da pesquisa, seus participantes e da elaboração da unidade curricular, detalhando a sequência didática, assim como o procedimento da coleta de dados.
Local da pesquisa e participantes
A presente pesquisa foi realizada na Escola Sesc de Ensino Médio, integrante do Polo Educacional Sesc, situado na Avenida Ayrton Senna, em Jacarepaguá. O câmpus possui 131 mil m² e conta com um espaço cultural que promove muitos espetáculos, cultura e lazer, e a Escola de Artes Dramáticas. Na instituição há biblioteca, laboratórios equipados de Biologia, Química, Física e Geografia, ginásio com quadra de areia, piscina, academia, sala de dança, quadras de tênis, quadra poliesportiva, espaço para jogos de raquete, sala de pilates e sala de luta. A escola conta ainda com sala de robótica, espaço maker e muitos outros espaços de aprendizagem. Uma verdadeira comunidade educativa completa que visa à formação integral do aluno.
Os alunos integrantes da pesquisa têm entre 13 e 16 anos e foram selecionados por meio de sorteio nos anos de 2021 e 2022, sendo externos ou residentes, oriundos de todos os estados da federação, compondo uma diversidade única com um modelo de ensino integral em tempo integral, preocupada com a sua formação completa. Os 30 alunos inscritos na disciplina MatLab - Laboratório de Matemática o fizeram de maneira opcional, sendo uma escolha dentre as 113 unidades curriculares optativas. Deles, 18 participaram da pesquisa.
Elaboração da disciplina eletiva - MatLab
O curso MatLab, de caráter semestral, teve encontros semanais com duração de uma hora e meia, com alunos divididos em duplas ou em grupos. A ementa de apresentação do curso está descrita como: “criação de protótipo de objeto de aprendizagem digital ou não, para o ensino e pesquisa de conteúdos matemáticos nos campos da Geometria Plana, Geometria Espacial e Funções; reflexão sobre os processos de ensino e aprendizagem da Matemática; estudo sobre a aplicação e necessidade da criação de um objeto que favoreça a aprendizagem; apresentação do produto e seu processo em formato de e-book”.
A motivação para o trabalho em grupo é incentivada por Vygotsky (1984), que afirma que a aprendizagem não se dá somente na relação professor-aluno, mas que é importante a integração entre os pares em atividades conjuntas e colaborativas. Corroborando as suas ideias (de que para facilitar a aprendizagem é necessário ter interação, participação e dinamismo), o curso foi fundamentado na metodologia de Design Thinking, já comentada.
Refletindo sobre o aprofundamento dos conteúdos e quais dentre eles seriam trabalhados, nos fundamentamos na ideologia de Papert (2021):
É um absurdo achar que só se deve aprender determinado conteúdo quando se tem sete anos e outro quando se tem oito. A ideia de um currículo linear lembra o sistema de produção em série industrial. Temos de aprender a perceber a necessidade de cada indivíduo. Ele é quem vai ditar o que precisa aprender, a que hora e com que intensidade.
Dessa forma, cada equipe de trabalho avaliou que conteúdo desejava trabalhar e qual seria o grau de aprofundamento, fazendo assim com que houvesse um real interesse pelo que se pesquisava.
Sequência didática
A seguir está o framework elaborado para a melhor organização da unidade curricular MatLab.
Sequência didática Unidade curricular: MatLab |
|
|
|
|
Estrutura |
|
|
|
|
|
|
|
|
|
|
1ª Etapa - Empatia |
Tempo Estimado: 1h30m |
Os grupos devem pesquisar e responder:
Os grupos devem criar um diário de bordo colaborativo e o professor deve ter acesso a ele. Sugestões: Padlet ou documento compartilhado no Google. O professor deve orientar sobre a importância do registro de cada etapa do processo. |
Fundamentação pedagógica |
“Um procedimento de pesquisa parece mais ambicioso, pois leva os alunos a construírem eles próprios a teoria” (Perrenoud, 2000, p. 38) Sobre o diário de bordo: “São a expressão do pensamento sobre uma situação concreta que, pelo seu significado, atribui a nossa atenção e merece a nossa reflexão. São descrições, devidamente contextualizadas, que revelam conhecimentos sobre algo que, normalmente, é complexo e sujeito a interpretação” (Alarcão, 2011, p. 56). |
Fundamentação tecnológica |
“Ferramentas como o Padlet, que apresentam características colaborativas, permitem a interação dos sujeitos difundindo ideias, cultura, democratizando as informações e aprendendo em um contexto diferente do presencial” (Silva; Lima, 2018). |
Estudo do tema |
Tempo estimado: 1h30m |
Caso os grupos não consigam decidir qual tema trabalhar, devem fazê-lo agora. Após a escolha do tema os alunos devem fazer um estudo para aprofundamento e saber qual será o foco do objeto de aprendizagem. Obs.: Ainda não é o momento de pensar no protótipo. |
2ª Etapa - Definição |
Tempo estimado: 1h30m |
Os alunos devem pesquisar sobre o “cliente”. Sugestão de criação digital no Wordwall, GeoGebra etc. |
Fundamentação tecnológica |
Moraes e Oliveira (2019) consideram que os jogos digitais educacionais motivam os alunos ao aprendizado, promovendo uma experiência positiva e satisfatória. Traduz-se, deste modo, em uma ferramenta para auxiliar no ensino e aprendizagem, pois além de motivar os alunos, ajuda na assimilação dos conteúdos, dentre outros benefícios dos jogos na educação. |
3ª Etapa – Ideação |
Tempo estimado: Dois encontros de 1h30m cada um. |
Momento do brainstorming Roda de conversa Cada grupo comenta seu planejamento e depois fazem uma discussão sobre a viabilidade dos projetos. |
4ª Etapa – Prototipar |
Tempo estimado: Quatro encontros de 1h30m cada um para o protótipo e 1h30 para o refinamento |
Criando a representação das ideias Refinamento Criação de questionário |
5ª Etapa – Provar |
Tempo estimado: 1h30 para as apresentações e 1h30 para os testes e feedbacks. |
Apresentação das equipes Cada grupo deve apresentar o seu protótipo. Após as apresentações, os grupos irão testar os produtos das outras equipes. |
Criação do e-book (manual) |
Tempo estimado: Três encontros de 1h30m cada um. Local para realização: Sala de aula. |
Hora de registrar! Sugestão: Canva. |
Avaliação - Encerramento |
Tempo estimado: 1h30m. |
Momento de aplicar um questionário para ajudar na autoavaliação dos alunos. Na tabela a seguir encontram-se algumas perguntas para montagem de um questionário. Após o preenchimento do questionário pelos alunos, eles devem formar uma roda de conversa para discutir as questões do formulário. Com a análise do questionário, o professor terá dados suficientes para aferir se o aluno terminou o curso com êxito, de tal forma que o aluno poderá receber o certificado de conclusão ou não. |
Perguntas para o questionário |
1. Como foi o processo de escolha do tema/conteúdo escolhido? |
2. Como foi feita a escolha do material para construção do protótipo? |
3. Como foi feita a divisão de tarefas da equipe? |
4. A elaboração do(s) protótipo(s) passou por algum contratempo? Explique detalhadamente. |
5.O grupo alcançou o cronograma planejado? |
6. Explique as facilidades e dificuldades encontradas ao longo do processo. |
7. Explique em detalhes como funciona o seu produto. |
8. Quais das competências abaixo você acredita ter trabalhado enquanto participava dos encontros do MatLab? Criatividade/Pensamento crítico/Comunicação/Colaboração/Atenção plena/Curiosidade/Autocontrole/Resiliência/Ética/Liderança/Metacognição (conhece seus próprios processos cognitivos)/Autonomia |
9. Como você avalia a sua participação no curso MatLab? (Nota [0,10]) |
10. O que você mudaria no curso? Responda com base em metas possíveis. |
11. Você recomendaria a disciplina MatLab para algum estudante? Por quê? |
Fundamentação pedagógica |
“É possível lançar mão de vários tipos de autoavaliação. A modalidade escrita é a mais comum e serve para diversas finalidades - além de aferir conteúdos, é uma boa opção para trabalhar com procedimentos” (Bibiano, 2018). |
Procedimento da coleta de dados
O processo de coleta de dados do presente trabalho segue o que Lakatos e Marconi (2017) chamam, nos Fundamentos de Metodologia Científica, de observação não estruturada, participante, em equipe e efetuada em laboratório.
Para que a coleta de dados pudesse ser iniciada, foi necessário o esclarecimento junto aos alunos sobre o projeto de pesquisa e sua livre participação. Dessa forma, aplicou-se o TCLE e/ou TALE antes da coleta de dados (que só pode ser realizada após a aprovação do projeto pelo Comitê de Ética em Pesquisa). Durante a pesquisa, respeitou-se tudo o que se refere às Resoluções nº 466/12 e 510/16, por se tratar de uma pesquisa que envolve seres humanos e com riscos mínimos. Tal pesquisa também está em consonância com a Resolução nº 674/2022, principalmente no que se refere no Art. 2º, parágrafo XIX, sobre a privacidade e o direito da pesquisa de manter o controle sobre suas escolhas e as informações pessoais dos participantes, resguardando sua intimidade, imagem e dados pessoais, como garantia de que não sofrerão invasões indevidas pelo controle público.
A observação não estruturada deve-se ao fato do seu caráter ser espontâneo e informal, apesar do planejamento das aulas. O mais importante nesta observação é verificar a evolução do aluno em sua participação nos grupos, sua autonomia e pensamento crítico. Embora seja participante, o pesquisador se integra ao grupo com a finalidade de obter informações e observar o ambiente real, deixando o processo ativo na mão dos alunos.
Foi aplicado um questionário online por meio do Google Forms e realizamos anotações sobre as impressões e observações de uma roda de conversa.
Apresentação e discussão dos resultados
Nesta seção, pretende-se fazer a análise dos dados de acordo com a análise de conteúdo. Bardin (2011) sugere que tal análise deve passar por três etapas: Pré-análise, Exploração do material e Tratamento dos resultados: inferência e interpretação.
Na primeira etapa foi possível conferir quais alunos fariam parte da pesquisa, de acordo com a entrega do TCLE e do TALE, conforme orienta o Comitê de Ética, de tal forma que as respostas correspondentes aos alunos 2, 10 e 14 não serão reveladas devido à falta de qualquer um dos documentos. Posteriormente, verificamos o questionário e os apontamentos feitos nas rodas de conversa para formular hipóteses e confrontar as respostas. Nessa fase, escolhemos focar nos itens competência e habilidades trabalhadas e nas dificuldades ao longo do processo de trabalho das equipes.
Na fase do tratamento dos resultados, optamos por enumerar e comparar as respostas do questionário com as anotações das rodas de conversa para verificarmos possíveis convergências ou divergências.
É possível observar na Figura 2 que um pouco menos de 48% acreditam que trabalharam a habilidade do pensamento crítico. Porém três respostas não foram contabilizadas, pois os alunos preencheram o questionário indevidamente com o recálculo; assim, 10 dos 18 respondentes acreditam ter trabalhado o pensamento crítico, o que corresponde a 55% do total. Ao analisar as respostas de acordo com o conteúdo trabalhado, é possível observar que integrantes do mesmo grupo divergem em suas respostas, o que nos leva a acreditar no desconhecimento do que é PC ou na possível incompreensão do conteúdo por parte de alguns alunos.
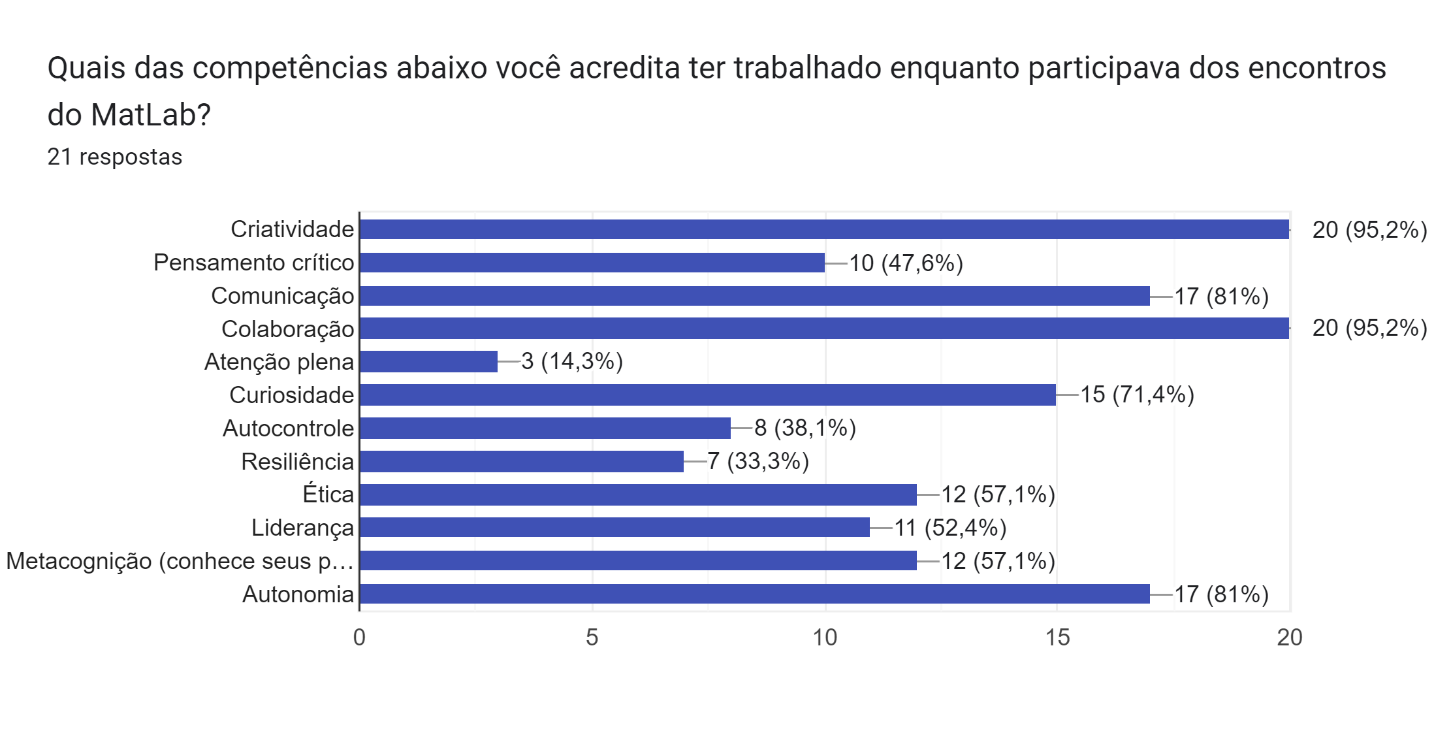
Figura 2: Gráfico correspondente às respostas da décima pergunta do questionário
Conforme mencionado, observamos que os processos sugeridos no artigo de Nada J. Alsaleh (2019), identificando a habilidade do pensamento crítico como interpretação, análise, avaliação, inferência, explicação e autorregulação, foram trabalhados nos grupos, pois eles foram capazes de refletir e explicar sobre os conteúdos, cumprindo com as etapas do curso.
Fazendo a retificação com o quantitativo de alunos, verificou-se que todos os alunos pesquisados marcaram a opção “criatividade”, habilidade mais fácil de ser reconhecida pelos alunos. Sobre a ‘colaboração’ apenas um aluno, entre os dezoito pesquisados, não marcou a opção, ou seja, 94% dos alunos acreditam ter trabalhado a habilidade. Vale observar que somente um aluno marcou apenas uma opção, o que nos leva a pensar na possibilidade de ele não ter percebido que poderia marcar mais de uma alternativa.
Verificando as respostas do questionário e aquelas direcionadas aos grupos nas rodas de conversa, identificamos as dificuldades encontradas, principalmente em relação ao planejamento. Por exemplo, o grupo da caixa de potências enfrentou dificuldades por não ter solicitado o material adequado. O grupo de ângulos havia pensado em um quebra-cabeças que não funcionou, precisando transformar o material em um jogo da memória. Já o grupo do plano cartesiano, não conseguiu concluir o plano naval e o grupo de frações percebeu que o dominó não estava em sua melhor lógica, sendo necessário repensar o projeto.
Durante a jornada da disciplina e após o seu término, verificamos a eficiência da proposta de sequência didática para o desenvolvimento do curso. O encadeamento lógico das tarefas, a partir das ideias do Design Thinking, serviu de forma adequada para as etapas do MatLab. As dificuldades encontradas foram relacionadas às eventuais ausências de alguns alunos, fazendo com que algumas etapas demorassem mais que outras, mas nada comprometeu o desenvolvimento do projeto.
Como consequência do curso, tivemos os primeiros protótipos e/ou produtos para o Laboratório de Matemática. Os alunos também elaboraram um e-book que serve como catálogo dos objetos do Laboratório de Matemática.
Ao longo do curso, criamos um manual em formato de e-book para facilitar a criação de um laboratório de Matemática aos docentes. No manual, consta a sequência didática em um formato simplificado e algumas dicas e orientações.
Considerações finais
A presente pesquisa, relacionada à criação de um Laboratório de Matemática, foi desenvolvida com as observações das aulas praticadas e a utilização dos passos descritos no framework, na intenção de alcançar alguns objetivos.
O primeiro objetivo específico (OE) trata da verificação da necessidade da criação de objetos de aprendizagem, base de todo este trabalho. Os alunos foram unânimes em perceber a importância da criação de materiais que facilitem suas vidas e a vida dos professores. Assim, eles concordaram em utilizar a metodologia do Design Thinking.
O segundo OE foi alcançado com a efetiva criação da sequência didática, baseada na metodologia do Design Thinking. Consequentemente, concretizamos o planejamento, formando uma disciplina eletiva consistente. Embora os alunos tenham encontrado algumas dificuldades, a maioria deles mostrou engajamento e o desejo de participar de tal elaboração. Tais dificuldades foram relacionadas aos pequenos atrasos na construção dos objetos, devido à dificuldade na sua construção, a um planejamento inadequado ou a uma ausência de alguns alunos.
Sobre as habilidades socioemocionais, percebemos, de forma discreta, o avanço no pensamento crítico em Matemática. O resultado de tal mensuração foi concluído ao observar a capacidade dos alunos em explicar todo o processo de criação, interpretando e analisando. Com o objeto de aprendizagem em mãos, conseguiram explicar um conteúdo com propriedade e todos concordaram ter avançado na criatividade, mesmo os alunos que não acreditavam ser criativos. O amadurecimento relacionado à autonomia é o mais evidente e, ao longo dos encontros, não era mais necessário dizer o que os alunos precisavam fazer. Não podemos deixar de salientar que o público pesquisado passou por um ou dois anos em aulas remotas, fazendo até mesmo rodízio na escola por conta da pandemia da covid-19.
Resgatando os objetivos, concluímos que após a constatação da necessidade de criação de objetos de aprendizagem, da modelagem e da execução da sequência didática por meio do Design Thinking, verificamos que habilidades como a autonomia, o pensamento crítico e a criatividade foram promovidas. Além disso, o desdobramento da sequência didática fundamentou a disciplina eletiva e resultou no início do Laboratório de Matemática. O processo sugerido é um caminho, mas não único e pode servir como um norte para quem o desejar.
Referências
ALARCÃO, I. Professores reflexivos em uma escola reflexiva. 8ª ed. São Paulo: Cortez, 2011.
ALSALEH, Nada J. Teaching critical thinking skills: Literature review. Tojet: The Turkish Online Journal of Educational Technology, Riyadh, v. 19, n° 1, p. 21-39, jan. 2019.
AUTOAVALIAÇÃO: como ajudar seus alunos nesse processo. Nova Escola, nº 432, 2018. Disponível em: https://novaescola.org.br/conteudo/432/autoavaliacao-como-ajudar-seus-alunos-nesse-processo. Acesso em: 4 out. 2022.
BARDIN, L. Análise de conteúdo. São Paulo: Edições 70, 2011.
BEAN, J. Engaging ideas: the professor’s guide to integrating writing, critical thinking, and active learning in the classroom. 2ª ed. San Francisco: Jossey-Bass, 2011.
BROWN, Tim. Design Thinking: uma metodologia poderosa para decretar o fim das velhas ideias. 10ª ed. Rio de Janeiro: Alta Books, 2010.
COURTNEY, E.; ACKERMAN, M. A. Big five personality traits: the Ocean model explained. Positive Psychology, 23 jun. 2017. Disponível em: https://positivepsychology.com/big-five-personality-theory/. Acesso em: 13 jan. 2023.
DESIGN THINKING: o que é e como aplicar em sua escola. Atena Educacional, 23 set. 2019. Disponível em: https://www.atenaeducacional.com.br/design-thinking-o-que-e-e-como-aplicar-em-sua-escola/. Acesso em: 14 jun. 2022.
DEWEY, J. The process and product of reflective activity: Psychological process and logical forms. In: BOYDSTON, J. (ed.). The later works of John Dewey. Carbondale: Southern Illinois University Press, 1933. v. 8, p. 171-186.
FIRDAUS, F. et al. Developing critical thinking skills of students in Mathematics learning. Journal of Education and Learning (EduLearn), v. 9, n° 3, 2015.
KURFISS, J. Critical thinking: Theory, research, practice, and possibilities. Washington: Association for the Study of Higher Education, 1988.
LAKATOS, E. M.; MARCONI, M. A. Fundamentos de metodologia científica. 8ª ed. São Paulo: Atlas, 2017.
PITHERS, R. & SODEN, R. Critical thinking in education: A review. Educational Research, v. 42, n° 3, p. 237-249, 2000.
PERRENOUD, P. Novas competências para ensinar – convite à viagem. Porto Alegre: Artmed, 2000.
SILVA, P. G.; LIMA, D. S. Padlet como ambiente virtual de aprendizagem na formação de profissionais da educação. Renote, Porto Alegre, v. 16, n° 1, 2018.
SIMON, H. A. The science of the artificial. 3ª ed. London: MIT Press, 1969.
SOUZA, A. F. Seymour Papert – A maior vantagem competitiva é a habilidade de aprender. Blog da Psicologia da Educação, 28 fev. 2021. Disponível em: https://www.ufrgs.br/psicoeduc/piaget/papert-habilidade-de-aprender/. Acesso em 13 jan. 2023.
VYGOTSKY, L.S. A formação social da mente. São Paulo: Martins Fontes, 1984.
Publicado em 03 de outubro de 2023
Como citar este artigo (ABNT)
PEREIRA, Gisele de Oliveira Ribeiro; JATOBÁ, Alessandro; CARVALHO, Paulo Vitor. Design Thinking na Educação: trabalhando com habilidades socioemocionais. Revista Educação Pública, Rio de Janeiro, v. 23, nº 38, 3 de outubro de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/38/design-thinking-na-educacao-trabalhando-com-habilidades-socioemocionais
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

