Uso do futebol como mediador no estudo do movimento
Francisco Fabilino de Freitas
Licenciado em Física (IFPI - Câmpus Picos)
Italo Marcos de Lima
Mestre em Ensino de Física, professor da Seduc/PI e do IFPI – Câmpus Oeiras
Haroldo Reis Alves de Macêdo
Doutor em Engenharia dos Materiais (IFPI - Câmpus José de Freitas)
A Cinemática estuda grandezas como posição, velocidade e aceleração de determinado sistema, sem se importar com as causas, sendo descrita por equações chamadas de funções horárias do movimento. Quando há interesse nas causas, por exemplo, nas forças e na energia, dá-se o nome de Dinâmica. Nessa parte da Física estudam-se as Leis de Newton e os conceitos relacionados à quantidade de movimento, assim como a energia e as leis de conservação.
Todavia, para um estudante de Física do Ensino Médio, por exemplo, não é suficiente apenas apresentar os conceitos em sala de aula, mostrando as equações envolvidas na disciplina. Fazer isso pode gerar um desinteresse dos estudantes pela matéria e associar os conceitos físicos da natureza apenas a problemas abstratos da Matemática (Borges, 2016). É preciso contextualizá-la com as vivências dos estudantes.
Borges (2016) ressalta, ainda, que tratar a Física como “problemas abstratos da Matemática” é um óbice comum no Brasil, fazendo com que o aluno acabe associando a disciplina à extensão da disciplina de Matemática, entendendo que o estudo dos fenômenos da natureza se resume apenas à aplicação de fórmulas.
A Física deve ser utilizada como um meio para se explicar fenômenos naturais e tecnológicos, presentes no cotidiano dos estudantes e necessários à compreensão do universo, no geral a partir de princípios, de leis e de modelos construídos por ela (Brasil, 2002).
Portanto, cabe ao professor de Física utilizar alternativas que favoreçam o aprendizado da disciplina, focando nos conceitos e em suas aplicações no cotidiano, pois assim o aluno se tornará mais interessado no aprendizado. O estudo de caso é um dos facilitadores desse processo, uma vez que faz o aluno analisar problemas reais e aplicá-los em sala. Linhares (2008) fala da importância dos estudos de caso ao afirmar que são questões de interesse dos discentes e que podem estimular a aquisição de conhecimentos e habilidades, pois se trata de uma forma de aplicação direta dos assuntos estudados em sala de aula sobre o mundo real.
De fácil observação por diversos fenômenos físicos, têm-se os esportes, fortemente ligados ao cotidiano da maioria dos estudantes. Como exemplo de esportes populares no Brasil, citamos o futebol e o vôlei. Em ambos os casos, os jogadores necessitam estar em constante movimento para que a partida seja executada. Assim, algumas grandezas físicas aparecem rotineiramente, como é o caso da velocidade e da posição da bola e dos jogadores, ou seja, durante uma partida é possível estudar Física, pois ela permite descrever os movimentos executados durante a partida.
O futebol é o esporte mais conhecido e jogado em todo o mundo (Franco, 2022). Devido a isso, a presença desse esporte na vida das pessoas é muito comum, sendo, portanto, perfeitamente viável identificar alguns conceitos da Física nos diversos lances desse esporte. Durante uma disputa de bola, por exemplo, os jogadores exercem contato físico uns com os outros, proporcionando a aplicação de forças de acordo com a terceira Lei de Newton. Durante o chute na bola há o fenômeno da colisão, dentre outros exemplos.
Sabendo da importância e da relevância desse esporte, é possível utilizá-lo como alternativa didática para auxiliar no ensino de Física, uma vez que existem vários tipos e ações a serem analisadas, como o escanteio, a troca de passes e o chute a gol. Pretende-se, então, utilizar esses lances como mediadores para a aplicação de conceitos relacionados ao movimento retilíneo uniforme (MRU) e ao movimento uniformemente variado (MUV). Assim, o objetivo principal deste trabalho é aplicar os conceitos de MRU e MUV tendo o futebol como objeto, a fim de facilitar a aprendizagem dos estudantes.
Cinemática
A Cinemática é a área da Mecânica que estuda o movimento dos corpos sem se preocupar com as causas (Tipler; Mosca, 2009). Por ela, definem-se as grandezas da Mecânica, como é o caso da posição, da velocidade e da aceleração dos corpos.
Para ilustrar o desenvolvimento da Cinemática, é interessante mostrar a construção de seu conceito sob a ótica de Aristóteles. Ele dividiu o movimento dos corpos em duas grandes classes: o movimento natural e o movimento violento (Feynman, 2008). “Aristóteles afirmava que o movimento natural decorre da ‘natureza’ de um objeto, dependendo de qual combinação dos quatro elementos, terra, água, ar e fogo, ele fosse feito” (Hewitt, 2015). Portanto, para ele, todos os objetos tinham seu lugar apropriado e determinado por natureza. Hewitt (2015) afirma sobre as ideias de Aristóteles: “um objeto mais pesado deveria esforçar-se mais fortemente. Portanto, argumenta Aristóteles, os objetos deveriam cair com rapidez proporcional a seus pesos: quanto mais pesado fosse o objeto, mais rápido deveria cair” (Hewitt, 2015). Além disso, Aristóteles também acreditava que “o movimento de corpos celestes, como por exemplo, estrelas e planetas, não obedecia às mesmas leis que os objetos terrestres” (Halliday; Resnick; Walker, 2012).
Uma segunda classificação de movimento, o movimento violento, por outro lado, era a classe de movimento associada ao ato de puxar e empurrar, ou seja, trata-se de um movimento imposto por algo ou alguém (Halliday; Resnick; Walker, 2012). Hewitt afirma que, de acordo com Aristóteles, o fato essencial sobre o movimento violento é que ele tinha uma causa externa e era comunicado aos objetos que se moviam não por si mesmos nem por sua “natureza”, mas por causa de empurrões e puxões (Hewitt, 2015).
As afirmações de Aristóteles a respeito do movimento dos corpos constituíram o início do pensamento científico, perdurando por quase 2.000 anos até que novas ideias surgiram e foram testadas experimentalmente.
Foi a partir das ideias de Galileu sobre o movimento que se iniciou o estudo da Cinemática que se conhece hoje. Graças a Galileu, foram definidos termos muito importantes como posição, velocidade e aceleração dos corpos. Essas grandezas são estudadas na forma escalar média e para o instantâneo, o que requer algumas aproximações para seu estudo em nível médio. Hewitt (2015, p. 41) diz que,
uma vez que a rapidez média é a distância total percorrida dividida pelo tempo total da viagem, ela não revela os diferentes valores de rapidez e as variações que podem ter ocorrido em intervalos de tempo mais curtos. Na maioria das vezes, experimentamos uma variedade de valores de rapidez, de modo que a rapidez média com frequência é completamente diferente dos valores da rapidez instantânea.
As equações características desse tipo de grandeza são mostradas abaixo:
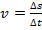 (Eq. 1)
(Eq. 1)
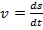 (Eq. 2),
(Eq. 2),
onde a equação (1) refere-se à velocidade escalar média, sendo
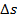 o deslocamento do objeto ao longo da trajetória e
o deslocamento do objeto ao longo da trajetória e
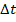 o tempo de percurso. Na equação (2), a velocidade instantânea tem
o tempo de percurso. Na equação (2), a velocidade instantânea tem
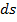 , que é o deslocamento efetuado pela partícula num tempo
, que é o deslocamento efetuado pela partícula num tempo
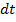 que tende a zero (Nussenzveig, 2013).
que tende a zero (Nussenzveig, 2013).
No entanto, pelas definições de Galileu, não bastam as definições de posição e velocidade. As leis de transformação de Galileu mostram que um corpo pode estar parado ou em movimento somente quando se define um referencial no qual se esteja realizando essas observações, ou seja, o movimento, nesse caso, é relativo (Feynman, 2008).
Aceleração média e instantânea
A velocidade no movimento retilíneo uniforme (MRU) é sempre constante, ou seja, não ocorrem variações em seu valor ao longo do tempo. No movimento uniformemente variado (MUV), no entanto, nota-se que, ao longo do tempo, o valor de sua velocidade varia linearmente com o tempo. A essa taxa de variação da velocidade com o tempo, dá-se o nome de aceleração (Nussenzveig, 2013).
Essa aceleração pode ser média ou instantânea. A aceleração média consiste em definir a velocidade da partícula analisada em diferentes pontos do trajeto e dividi-la pelo tempo total gasto pela partícula ao deslocar-se. Já a aceleração instantânea consiste em analisar como a velocidade varia com o tempo, num determinado instante bem definido da trajetória (Halliday; Resnick; Walker, 2012). Essa aceleração pode ser de dois tipos: aceleração progressiva, que é o ganho de velocidade com o tempo, ou aceleração retrógrada, que é a diminuição da velocidade com o tempo (Tipler; Mosca, 2009).
Além de relacionar-se com a velocidade, a aceleração também pode ser relacionada ao deslocamento de determinada partícula. Para isso, usa-se o conceito de equação horária da posição ou a equação de Torricelli (Feynman, 2008).
Equação horária da posição
A equação horária da posição determina a posição de qualquer partícula em função do tempo. “A que distância um objeto cai é completamente diferente de quão rápido ele cai. Com seus planos inclinados, Galileu descobriu que a distância que um objeto uniformemente acelerado percorre é proporcional ao quadrado do tempo” (Hewitt, 2015, p. 48). No geral, quando existe alguma aceleração no sistema analisado, define-se a equação horária da posição como:
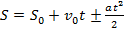 (Eq. 3),
(Eq. 3),
em que o termo (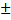 ) está relacionado ao tipo de aceleração, se é do tipo progressiva ou retrógrada. Note que, como havia afirmado Galileu, a posição é proporcional ao quadrado do tempo, ou seja, trata-se de uma função quadrática (Nussenzveig, 2013).
) está relacionado ao tipo de aceleração, se é do tipo progressiva ou retrógrada. Note que, como havia afirmado Galileu, a posição é proporcional ao quadrado do tempo, ou seja, trata-se de uma função quadrática (Nussenzveig, 2013).
É interessante ressaltar que
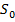 é uma constante que determina a posição da partícula no instante inicial
é uma constante que determina a posição da partícula no instante inicial
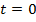 , e
, e
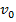 determina a velocidade inicial do sistema analisado;
determina a velocidade inicial do sistema analisado;
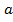 é a aceleração do sistema.
é a aceleração do sistema.
Quando a aceleração da partícula é desprezível, ou seja, para 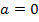 , o termo que depende quadraticamente do tempo desaparece, restando apenas a equação (4):
, o termo que depende quadraticamente do tempo desaparece, restando apenas a equação (4):
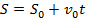 (Eq. 4)
(Eq. 4)
Ou seja, quando não há aceleração, a equação (4) se torna o caso particular do MRU. Como exemplo de aplicação, pode-se citar o movimento de um jogador que corre na direção de uma bola para bater um pênalti. Sabendo o tempo 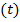 que ele demora para percorrer o trajeto a uma certa velocidade (
que ele demora para percorrer o trajeto a uma certa velocidade (
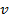 ), pode-se determinar a distância percorrida pelo jogador em qualquer instante de tempo (Tipler; Mosca, 2009).
), pode-se determinar a distância percorrida pelo jogador em qualquer instante de tempo (Tipler; Mosca, 2009).
Equação horária da velocidade
Tal como a equação horária da posição, a equação horária da velocidade estabelece a velocidade da partícula em função do tempo, ou seja, estabelece qual o valor para diferentes instantes de tempo. Para o caso em que a aceleração aparece no sistema, tem-se que a equação horária da velocidade será dada pela equação (5).
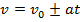 (Eq. 5)
(Eq. 5)
Contudo, para a aceleração nula, deve-se utilizar a equação (2) como sendo a equação horária da velocidade. A equação (5), tal como a equação (4), é uma função afim.
Equação de Torricelli
Determinar a velocidade de uma partícula sem saber o tempo é um problema que foi solucionado por Torricelli, usando a expressão matemática que leva seu nome. É possível saber como a velocidade de uma partícula varia de acordo com sua posição, pois o parâmetro que mede o tempo de percurso não entra na equação. De maneira informal, ela pode ser entendida como sendo uma equação que determina a velocidade para problemas cujo tempo de percurso da partícula se torna uma incógnita. Para tal, pode-se definir uma equação envolvendo apenas as velocidades finais e iniciais, a aceleração e a variação de posição da partícula, tal como mostra a equação (6).
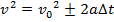 (Eq. 6)
(Eq. 6)
Como forma de aplicação da equação (6) em situações do cotidiano, pode-se estudar o caso de um jogador correndo pelo campo. Ao ver como sua velocidade varia com o tempo, é possível determinar a aceleração e, consequentemente, determinar seu deslocamento. Imagine, por exemplo, que um jogador começa a correr a partir do centro do campo. Ele inicia sua velocidade com
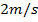 , porém, após dois segundos, nota-se que sua velocidade é de
, porém, após dois segundos, nota-se que sua velocidade é de
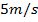 . Partindo disso, pode-se determinar sua aceleração dividindo a velocidade pelo tempo. Conclui-se, portanto, que sua aceleração será de
. Partindo disso, pode-se determinar sua aceleração dividindo a velocidade pelo tempo. Conclui-se, portanto, que sua aceleração será de
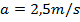 . Nesse instante, sua posição seria, de acordo com a equação (6), igual a
. Nesse instante, sua posição seria, de acordo com a equação (6), igual a
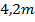 .
.
Física, futebol e movimento
As aplicações da Física no esporte podem ser encontradas com abundância na literatura. O estudo dessas aplicações é de suma importância para que o professor possua artifícios para melhorar as aulas de Física no Ensino Fundamental e no Ensino Médio. Duarte e Okuno (2012, p. 12) afirmam que
a distinção entre movimento e repouso, no futebol, aparece na regra 8 das Regras do Jogo de Futebol 2009/2010 da FIFA. A regra 8 (o início e o reinício de jogo) diz que, antes de o jogo ser (re)iniciado, “a bola estará imóvel no ponto central” e que “a bola estará em jogo no momento em que for chutada e se mover para a frente”.
De acordo com o mesmo autor, a Física classifica os movimentos como sendo de translação e rotação. É interessante notar que, no futebol, ambos os movimentos podem ser observados quando um jogador chuta a bola. Duarte e Okuno (2012, p. 12) ressaltam:
movimentos mistos (translação mais rotação) são aqueles que combinam os movimentos de translação e rotação. A bola chutada “com efeito” é um exemplo de movimento misto se considerarmos o movimento dela até o gol (translação) e o giro da bola em torno de si mesma (rotação).
Vê-se, portanto, que são muitas as possibilidades de estudo dos movimentos numa partida de futebol e que nas próprias regras do jogo há a definição do que é repouso e movimento. Em diversos tipos de lances é possível ver a Física. Assim, apresentamos nossa proposta de uso de lances de futebol para o estudo do movimento.
Proposta para as aulas de Física usando o futebol
Nas aulas, os assuntos serão trabalhados conforme o método tradicional. Primeiramente, será apresentado o conteúdo, mostrando todas as definições e equações necessárias para o entendimento do MRU e do MUV. Para fixação, serão apresentados alguns lances do futebol disponíveis na internet referentes a cada conteúdo abordado, conforme apresentado no Quadro 1.
Quadro 1: Sequência de aulas por conteúdo relacionado a lances numa partida de futebol
Sequência da aula |
Conteúdo |
Período |
Lance |
Link para visualização |
1° aula |
Velocidade escalar média e velocidade instantânea |
Uma aula de 50 min |
Troca de passes do meio de campo até o gol |
|
2° aula |
Equação horária da posição no MRU |
Uma aula de 50 min |
Chute ao gol – o gol mais rápido do mundo |
|
3° aula |
Equação horária da posição no MUV |
Uma aula de 50 min |
Escanteio |
|
4° aula |
Classificação do movimento |
Uma aula de 50 min |
“Chapéu” |
O campo utilizado como exemplo para construção do trabalho é o Estádio Jornalista Mário Filho, popularmente conhecido como Maracanã, no Rio de Janeiro. O estádio tem as seguintes medidas oficiais: gramado, 110m x 75m (Figura 1), área total de 186.638m2 e capacidade para 78.838 espectadores.

Figura 1: Estádio do Maracanã em dia de jogo, com as medidas do campo
Fonte: Adaptado de https://www.estadios.net/estadio-do-maracana/. Acesso em:18 fev. 2023.
Na primeira aula, o professor deve mostrar o vídeo do lance da troca de passes do centro de campo até o gol e pedir, como exercício, que os alunos determinem a velocidade média dos jogadores, usando a equação (1). Para tanto, devem considerar as medidas oficiais do Maracanã e o tempo entre o início do passe no meio de campo até o momento do gol. Para obter os tempos, os estudantes devem pausar o vídeo nos momentos citados e anotar a diferença de tempo em segundos. Na Figura 2, apresentamos os valores de ΔS e Δt, usados para o cálculo com informações obtidas a partir da observação do vídeo.
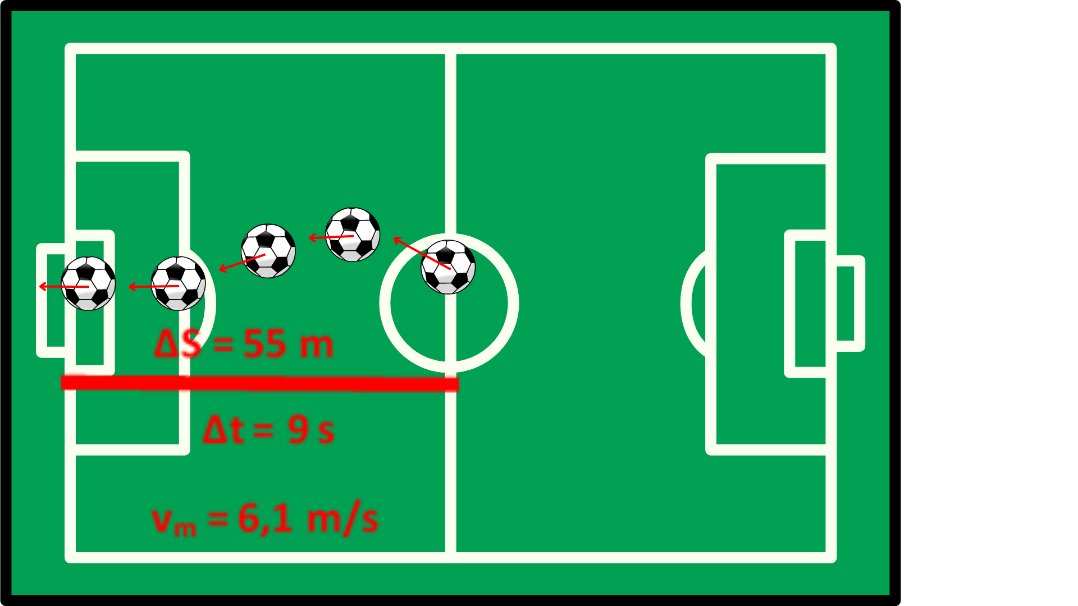
Figura 2: Dados resumidos para cálculo da velocidade média, obtidos no vídeo da aula 1
Após os estudantes calcularem a velocidade média da bola do meio de campo ao gol, o professor deve contextualizar, levantando questionamentos como:
- será essa a velocidade de cada jogador?
- a velocidade dos jogadores é semelhante à de um corredor profissional de 100m rasos, por exemplo?
- por que considerar o movimento como MRU e não MUV?
- a bola não foi em linha reta; por que no cálculo foi considerada uma linha reta? Neste questionamento, o professor deve apresentar as definições de distância percorrida e deslocamento.
Em seguida, sabendo a velocidade média, o professor deve solicitar que os estudantes determinem a equação horária da posição para a bola, considerando o deslocamento do centro de campo como posição inicial até o gol (posição final). Posteriormente, os estudantes devem ser orientados a construir um gráfico ΔS e Δt utilizando os seguintes tempos: 1,0s, 3,0s, 6,0s e 9,0s. O gráfico construído pelos estudantes deve ser semelhante ao da Figura 3.
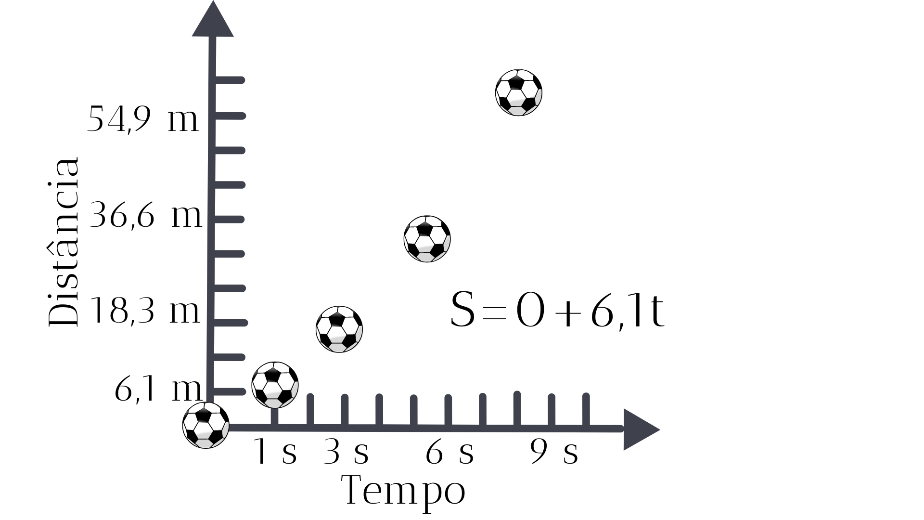
Figura 3: Modelo do gráfico e função horária que os estudantes devem elaborar
Na segunda aula, deve ser apresentado o vídeo do gol mais rápido do mundo, quando o jogador chuta a bola do meio de campo e consegue fazer o gol, considerando a distância do centro de campo até o gol mencionada na aula 1. O professor deve solicitar que os estudantes sigam o mesmo procedimento, de forma a fixar as definições e as equações que descrevem o MRU. Sugere-se uma comparação entre os valores obtidos para a velocidade média e uma discussão sobre os fatores que levaram à variação da velocidade entre o caso da primeira e da segunda aulas.
Para a terceira aula, os estudantes já devem ter conhecimento das equações do MUV. Sabendo a distância entre o escanteio e o gol, analisando quanto tempo levou para a bola chegar ao gol, o professor deve propor que os alunos determinem a aceleração da bola, usando a equação horária do espaço para o MUV, e quanto tempo demoraria para percorrer o dobro dessa distância, usando a equação (3). Vale ressaltar que nos casos citados não há variação apenas na velocidade, mas também de direção de movimento. Nessa aula, o professor pode explorar a construção de gráficos que envolvam a posição, o tempo, a velocidade e a aceleração, conforme já exemplificado na Figura 3.
Na quarta aula, o professor deve usar o vídeo que mostra um lance conhecido como “chapéu” e trabalhar a classificação do movimento quanto ao sentido (progressivo ou retrógado) e quanto à variação da velocidade (acelerado ou retardado). Na Figura 4, apresentamos qual deve ser o comportamento do gráfico. Na subida da bola, a distância aumenta com o tempo e por isso é progressivo, porém a velocidade diminui e por isso é retardado, até que a bola chega à sua altura máxima e então o movimento se inverte, diminuindo a distância com o progresso do tempo. Assim, o movimento é chamado de retrógrado, e a velocidade aumenta com o tempo, sendo então chamado de acelerado.
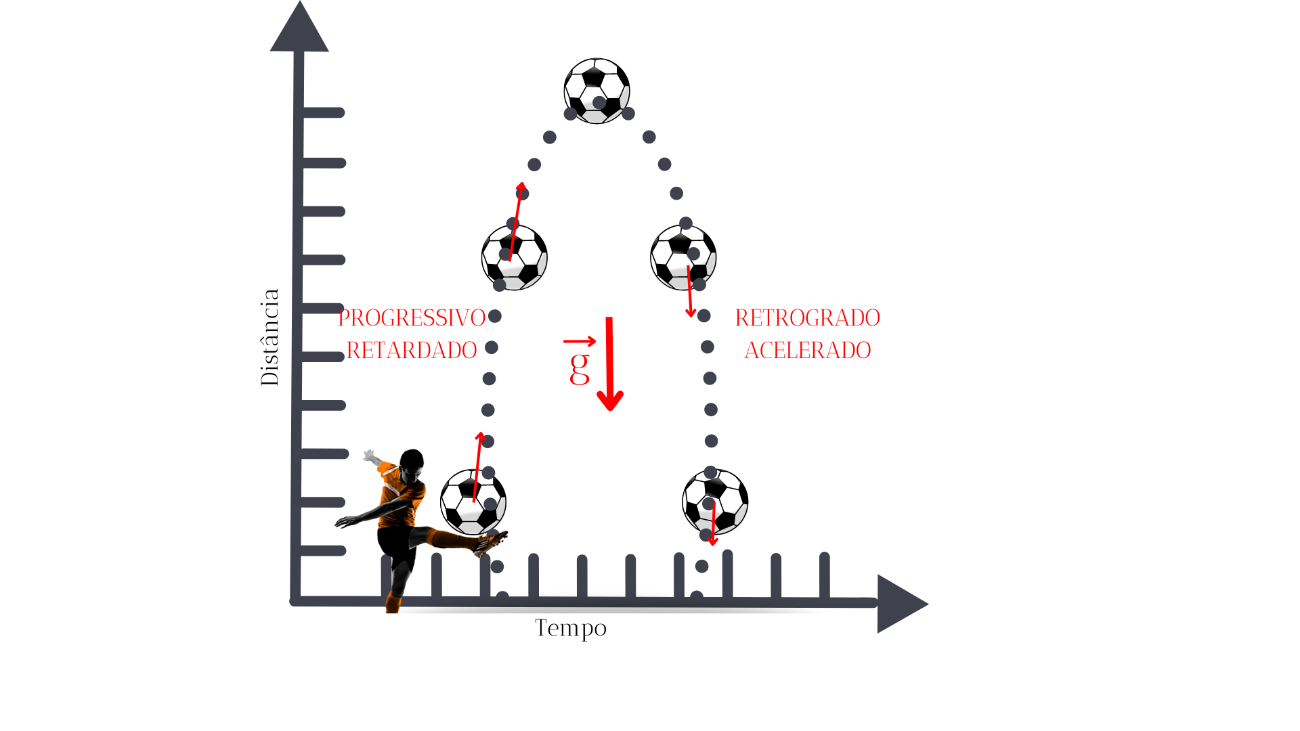
Figura 4: Gráfico da classificação do movimento para o lance do “chapéu”.
Para finalizar essa aula, o professor deve levantar um questionamento quanto ao sentido da gravidade 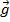 . Se mudarmos, inverteremos o sentido da gravidade. Assim, como ficaria a classificação do movimento? Após os esclarecimentos necessários, o professor deve solicitar que os estudantes façam um gráfico v x t para o lance do “chapéu” apresentado no vídeo.
. Se mudarmos, inverteremos o sentido da gravidade. Assim, como ficaria a classificação do movimento? Após os esclarecimentos necessários, o professor deve solicitar que os estudantes façam um gráfico v x t para o lance do “chapéu” apresentado no vídeo.
Expectativa de aprendizado por parte dos estudantes
Espera-se que, com a análise física desses lances rotineiros no futebol, os estudantes aprendam a obter as equações horárias do MRU e do MUV, bem como aprendam a construir e a analisar os gráficos desses movimentos, classificando-os adequadamente.
Considerações finais
Nessa proposta didática, utilizamos lances do futebol como mediadores na aplicação dos conceitos de MRU e MUV. Pesquisar sobre lances de futebol torna possível compreender que teoria e prática caminham na mesma direção e que os experimentos são fundamentais no ramo da Física.
Com a metodologia descrita, acreditamos ser possível adquirir importantes aprendizados acerca dos conceitos físicos abordados, além de promover habilidades que permitem a construção e a análise de gráficos, extrapolando assim as formalidades do ensino tradicional e atendendo aos objetivos previstos na legislação da educação brasileira.
A aplicação desta proposta com estudantes do 1° ano do Ensino Médio participantes das atividades do Programa de Residência Pedagógica mostrou resultados satisfatórios que foram medidos com base no rendimento das notas dos estudantes.
Referências
BORGES, L. B. Ensino e aprendizagem de Física: contribuições da teoria de Davydov. 2016. 154f. Tese (Doutorado em Educação) - Pontifícia Universidade Católica de Goiás, Goiânia, 2016.
BRASIL. Ministério da Educação. Secretaria de Ensino Médio e Tecnológico. Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais: Ciências da Natureza, Matemática e suas Tecnologias. Brasília: MEC, 2002.
DUARTE, M.; OKUNO, E. Física do futebol: Mecânica. São Paulo: Oficina de Textos, 2012.
FEYNMAN, R. P.; LEIGHTON, R. B.; SANDS, M. Lições de Física de Feynman. Porto Alegre: Bookman, 2008.
FRANCO, G. História do Futebol. Brasil Escola. 2022. Disponível em: https://brasilescola.uol.com.br/educacao-fisica/historia-do-futebol.htm. Acesso em: 29 jan. 2022.
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de Física. Rio de Janeiro: LTC, 2012.
HEWITT, P. G. Física conceitual. Porto Alegre: Bookman, 2015.
LINHARES, M. P.; REIS, E. M. Estudos de caso como estratégia de ensino na formação de professores de Física. Ciência & Educação, v. 14, n° 3, p. 555-574, 2008.
NUSSENZVEIG, H. M. Curso de Física Básica. 5ª ed. São Paulo: Edgard Blücher, 2013.
TIPLER, P. A.; MOSCA, G. Física para cientistas e engenheiros. Rio de Janeiro: LTC, 2009.
Publicado em 21 de novembro de 2023
Como citar este artigo (ABNT)
FREITAS, Francisco Fabilino de; LIMA, Italo Marcos de; MACÊDO, Haroldo Reis Alves de. Uso do futebol como mediador no estudo do movimento. Revista Educação Pública, Rio de Janeiro, v. 23, nº 45, 21 de novembro de 2023. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/23/45/uso-do-futebol-como-mediador-no-estudo-do-movimento
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

