A criptografia de Blakley como elemento motivador no ensino de Matemática

Conforme D’Ambrosio (2007) observou, as abordagens de ensino tradicionais já não são tão eficazes quanto antes, o que pode levar à desmotivação dos alunos em relação às aulas de Matemática. Isso resulta em perguntas comuns, como "Por que estou aprendendo isso?" ou "Como isso será útil na minha vida?". Muitos professores têm dificuldade em lidar com essas questões em suas práticas de ensino. Este trabalho tem como objetivo ajudar os professores em sala de aula, complementando sua prática pedagógica no ensino da Matemática, apresentando a criptografia como ferramenta motivacional para alguns tópicos.

A criptografia, técnica que envolve a codificação de informações para garantir sua segurança e privacidade, pode ser uma ferramenta útil no aprendizado da Matemática na escola. Além de ser um assunto fascinante por si só, a criptografia pode ajudar a motivar os alunos a estudar Matemática, pois envolve conceitos importantes como Álgebra, Geometria e teoria dos números. Além disso, a criptografia pode contribuir para desenvolver habilidades importantes, como pensamento lógico, resolução de problemas e trabalho em equipe. Com o aumento da importância da segurança de dados na sociedade atual, a compreensão dos princípios básicos da criptografia pode ser uma habilidade valiosa para os estudantes em seu futuro profissional. Nesse sentido, a introdução à criptografia neste trabalho para o ensino da Matemática tende a ser uma abordagem inovadora e interessante, tornando o aprendizado mais significativo e relevante para os alunos.

Os documentos curriculares brasileiros e o trabalho com temáticas transversais

Muito tem sido debatido a respeito dos temas transversais presentes em vários documentos legais da educação, como a Base Nacional Comum Curricular (BNCC) e os Parâmetros Curriculares Nacionais (PCN), dentre outros. Isso ocorre pela importância de abordar assuntos envolvendo questões sociais e a interdisciplinaridade. Os PCN, mais especificamente aquele para o Ensino Médio, destacam a importância da abordagem interdisciplinar e contextualizada com o objetivo de tirar o educando do estado de espectador passivo, estimulando a percepção dos estudantes para as relações entre os conteúdos disciplinares, conforme afirma Kranz (2022). Os temas contemporâneos transversais (TCT), presentes na BNCC, destacam uma abordagem ao longo do currículo escolar de forma transversal e integradora, com o objetivo de tratar de temáticas de interesse e relevância para a plena formação do educando.

Além disso, a Lei de Diretrizes e Bases da Educação Nacional (LDBEN) aborda as seguintes finalidades presentes no currículo de Matemática do Ensino Médio:

1. a consolidação e o aprofundamento dos conhecimentos adquiridos no Ensino Fundamental, possibilitando o prosseguimento de estudos;
2. a preparação básica para o trabalho e a cidadania do educando, para continuar aprendendo, de modo a ser capaz de se adaptar com flexibilidade a novas condições de ocupação ou aperfeiçoamento posteriores;
3. o aprimoramento do educando como pessoa humana, incluindo a formação ética e o desenvolvimento da autonomia intelectual e do pensamento crítico;
4. a compreensão dos fundamentos científico-tecnológicos dos processos produtivos, relacionando a teoria com a prática no ensino de cada disciplina (Brasil, 2017, p. 26).

Temos também as Orientações Curriculares do Ensino Médio (OCEM), que buscam destacar a presença de tais temáticas como forma de significar, relacionar e mostrar a aplicabilidade de conteúdos abordados em sala de aula (Kranz, 2022). De acordo com a OCEM, espera-se que, ao concluir o Ensino Médio, o educando seja capaz de resolver problemas práticos do cotidiano; a BNCC [EM13MAT301] complementa: ''que envolvem equações lineares simultâneas, usando técnicas algébricas e gráficas, com ou sem apoio de tecnologias digitais" (Brasil, 2015, p. 536), como modelar fenômenos em outras áreas do conhecimento. A Matemática é uma ciência com características próprias, um conhecimento social e historicamente construído.

Diante do exposto, podemos notar a relevância do tratamento de temáticas transversais que contribuem para a formação plena do educando, buscando relacioná-las aos conhecimentos abordados em sala de aula com aplicabilidade social. O presente trabalho busca utilizar a criptografia para introduzir, revisar, reforçar e aprofundar alguns conteúdos matemáticos, fortalecendo o ensino da Matemática a fim de torná-lo significativo.

Criptografia

A palavra criptografia tem origem nas palavras gregas ''kryptós" e ''gráphein", que significam escondido e escrita, respectivamente. Logo, a criptografia é a técnica capaz de reescrever mensagens, números e até mesmo realizar cálculos matemáticos de forma oculta, em que apenas o destinatário é capaz de decifrá-los e compreendê-los.

A criptografia surgiu da necessidade de realizar trocas de mensagens sigilosas de forma segura, posteriormente se estendendo aos cálculos. Há indícios de seu uso desde 1900 a.C., no Egito. Entretanto, ficou mais evidente durante a Segunda Guerra Mundial com a máquina de enigma, utilizada para a comunicação alemã, principalmente entre os comandos e as embarcações navais.

Os métodos criptográficos são classificados como clássicos e modernos. Os pertencentes à criptografia clássica são de transposição, que consiste em embaralhar a ordem dos caracteres das mensagens, ou de substituição, que utilizam tabelas definidas previamente para substituir um ou mais caractere da mensagem. O Scytale, a Tumba de Khnumhotep II, a Cifra de César e a Cifra de Vigenère são exemplos da criptografia clássica.

Os métodos pertencentes à criptografia moderna são divididos em chaves simétricas, que consistem em ter apenas uma chave para cifrar e decifrar a mensagem, e chaves assimétricas, que consistem em utilizar um par de chaves, uma privada e outra pública, no processo. A chave privada decifra a mensagem e a chave pública cifra. RSA, Diffie-Hellman, AES e RC4 são exemplos da criptografia moderna.

Inicialmente, a criptografia era usada principalmente para fins militares. Hoje, ela é usada para os mais variados fins: comunicação, transações bancárias, votação, assinatura digital, cálculos matemáticos e navegadores de internet, entre outros. Ela percorre desde métodos simples até algoritmos mais complexos, dependendo da sua aplicabilidade.

Como afirma Borges (2008), com a criptografia podemos partir de conceitos elementares de contagem até chegar às problematizações, conceitos abordados em departamentos de Matemática em universidades. Cabe ao professor direcionar essa aplicabilidade, levando em consideração o grau de entendimento matemático dos educandos. Em Tavares (2017), temos um exemplo de aplicação da criptografia para estudo das operações matriciais direcionado à Educação Básica. Em Lunkes (2022) está um exemplo de aplicação da criptografia para o estudo de homomorfismo, temática para o Ensino Superior.

Com isso, evidenciamos como a temática é atual e do cotidiano do educando, possibilitando atividades didáticas matemáticas que exploram a codificação e a decodificação de mensagens, possibilitando ao educando autonomia para realizar uma comunicação cifrada, além de explorar a criação de estratégias na resolução de problemas.

Esquema de Blakley e sua fundamentação matemática

O esquema criptográfico de Blakley, proposto por Blakley (1979), pertence ao método Secret Sharing (“segredo compartilhado”, em inglês), cujo objetivo é particionar o segredo e dividir com seus n participantes, sendo necessária a união de pelo menos k desses participantes.

Uma contextualização do método de Secret Sharing seria a abertura do cofre do Banco Central, por exemplo. Ao colocar o código-chave do cofre na posse de apenas uma pessoa, o banco corre diversos riscos: a pessoa pode ser sequestrada para ser recuperado o código-chave, pode extraviar valores para a sua própria conta ou simplesmente perder o código-chave, perdendo o acesso ao cofre. Devido aos riscos, uma alternativa seria particionar o código-chave, distribuindo-o entre pessoas de alto poder. Para a abertura do cofre seria necessária a combinação predeterminada dessas pessoas. Com isso, conseguimos garantir maior segurança ao código.

O método se baseia na resolução do sistema linear. Os segredos são o conjunto de todas as coordenadas da resolução do sistema, conforme Shamsoshoara (2019). Temos como fundamentação matemática para esse método a resolução do sistema linear e a representação de operações envolvendo matrizes, além da Aritmética modular, temáticas abordadas na Educação Básica, mais especificamente no Ensino Médio.

O método consiste em selecionar o segredo a ser cifrado, construindo um ponto com ele para, posteriormente, traçar planos que passem pelo ponto em questão. Cada participante do processo recebe coeficientes de um dos planos. O segredo será a resolução do sistema linear composto pelos planos. Para a sua decifragem, é necessária a união de pelo menos k desses participantes.

Exemplo numérico

Para realizar um exemplo numérico desse método, iremos utilizar o exemplo presente no trabalho de Shamsoshoara (2019). Seu objetivo é esconder o segredo 42. Para isso, escolhemos de forma aleatória os valores 29, para a coordenada y, e 57, para a coordenada z. Temos o ponto (42, 29, 57) para cifrar. Para isso, iremos criar os hiperplanos que passam por tal ponto. Para isso, escolhemos de forma aleatória os valores de a e b e calculamos 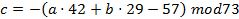. Assim, conseguimos construir os hiperplanos escritos da seguinte forma: 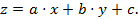 Teremos, então, o seguinte sistema linear:

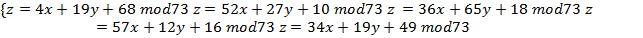
Reescrevendo em forma de matriz, há:

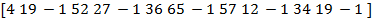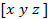A =             x =            B =

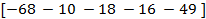
e cada participante receberá as seguintes chaves:

k1 = (4, 19, −1, −68),
k2= (52, 27, −1, −10),
k3 = (36, 65, −1, −18),
k4 = (57, 12, −1, −16),
k5 = (34, 19, −1, −49).

Utilizando o esquema (3,5) de Blakley, ou seja, dos cinco participantes do processo criptográfico, apenas três se juntaram para recuperar o segredo:

A =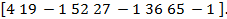

Ao calcularmos o determinante, teremos 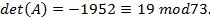 Utilizando o cofator (ou matriz adjunta em algumas literaturas) para calcular a matriz inversa, teremos:

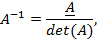
Então:

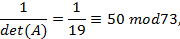
pois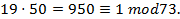

Calculando o cofator, teremos:

.

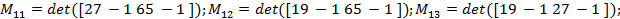
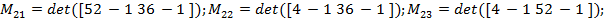
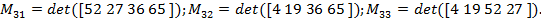
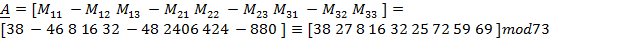Aplicando os valores encontrados na fórmula:

.

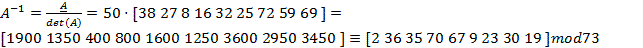Com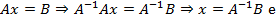o  sendo 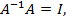 temos:

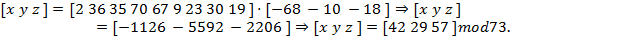
Assim, foi possível recuperar o segredo presente na variável x = 42.

Resultados e discussões

O presente trabalho tem como principal objetivo complementar a prática pedagógica de ensino da Matemática no processo de ensino-aprendizagem. A criptografia permite introduzir, revisar, reforçar e/ou aprofundar alguns conteúdos matemáticos presentes em sala de aula, conforme apresenta a BNCC. Como Olgin (2011) defende, por meio da Matemática estudada em aula a criptografia entra como recurso didático que podemos utilizar a fim de aguçar a curiosidade do educando, contextualizando-o a respeito das problemáticas reais que lhe cercam, como a respeito da segurança de dados pessoais.

Com atividades utilizando a criptografia, conseguimos explorar a concentração do educando, o trabalho em equipe e as estratégias para a resolução de problemas, além de aliar os conteúdos matemáticos estudados em aula, como no caso do Esquema de Blakley, apresentado neste trabalho, que aborda a resolução de sistemas lineares, bem como a Aritmética modular.

Referências

BLAKLEY, George Robert. Safeguarding cryptographic keys. In: Managing Requirements Knowledge, International Workshop on IEEE Computer Society, p. 313, 1979.

BORGES, F. Criptografia como ferramenta para o ensino de Matemática. SBMAC. Anais... p. 822, 2008.

BRASIL. Ministério da Educação. Secretaria da Educação Básica. Orientações curriculares para o Ensino Médio: Ciências da Natureza. v. 2. Brasília: MEC, 2008.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: MEC, 2015.

BRASIL. Lei de Diretrizes e Bases da Educação Nacional. Brasília: Senado Federal, 2017.

D'AMBROSIO, Ubiratan. Educação Matemática: da teoria à prática. Campinas: Papirus, 2007.

KRANZ, Bárbara Elisa; OLGIN, Clarissa de Assis. Uma abordagem com o tema criptografia no currículo de Matemática. Perspectivas da Educação Matemática, v. 15, n° 40, p. 1-20, 2022.

LUNKES, Aline de L. Z.; BORGES, Fábio. Sobre a aplicação de homomorfismo na criptografia. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics, v. 9, n° 1, 2022.

OLGIN, C. de A. Currículo no Ensino Médio: uma experiência com o tema criptografia. Tese (Doutorado em Ensino de Ciências e Matemática) – Universidade Luterana do Brasil, Canoas, 2011.

SHAMSOSHOARA, Alireza. Overview of Blakley's Secret Sharing Scheme. School of Informatics, Computing and Cyber Systems, Department of Mathematics & Statistics, Northern Arizona University. Flagstaff, janeiro de 2019.

TAVARES, N. P. et al. Criptografia: Uma ferramenta de ensino das operações matriciais. In: IV CONEDU, João Pessoa. Anais... Campina Grande: Conedu, 2017.