Uma experiência de aplicação do GeoGebra no ensino da função polinomial do 2º grau
Roberto Marques da Silva
Pós-graduando em Didática (IFMG - câmpus Arcos)
Joice Stella de Melo Rocha
Professora do IFMG - câmpus Arcos
São inúmeras e crescentes as inovações para integrar as mídias nos estudos, nas produções textuais, nas imagens, nos vídeos e nas redes sociais, no uso de diversos aplicativos pedagógicos ou não. Logo, há uma tendência ao uso das tecnologias de informação e comunicação (TIC), como afirmou Papert (1998), “há um forte indício de que a escola na forma que conhecemos, e que nossos pais e avós conheceram, precisa mudar radicalmente”. Ele reitera que “quando as tecnologias eram caras e distantes, qualquer proposta parecia radical. Atualmente, com fácil acesso, há necessidade de se preparar para um mundo cada vez mais informatizado que estimula os cidadãos a buscarem o novo” (Papert, 1998. p. 12).
Para Sá e Machado (2017, p. 1), “o uso das tecnologias na sala de aula vem se tornando uma ferramenta de grande importância, pois consegue auxiliar tanto o professor quanto o aluno na explicação e na compreensão dos conteúdos”. Assim, se percebe a importância das tecnologias digitais para o desenvolvimento das práticas pedagógicas dos professores, tornando o ensino da Matemática, por exemplo, mais tecnológico. Isso leva os alunos a tomarem consciência das infinitas possibilidades de acesso ao conhecimento que eles podem desenvolver.
Os usos das tecnologias digitais tornam as aulas mais atrativas e os alunos têm a oportunidade de aprender de maneira dinâmica e motivada. Conforme Kenski (2007, p. 46), “não há dúvida de que as novas tecnologias de comunicação e informação trouxeram mudanças consideráveis e positivas para a educação”.
Nessa perspectiva, o uso das tecnologias digitais no ambiente escolar de forma crítica e reflexiva pode vir a ser um meio de integralização do indivíduo em uma sociedade mais tecnológica, mas isso requer dele competências e habilidades que o capacitem a lidar com esse ambiente. Conforme Mercado (2002, p. 12), “na chamada sociedade da informação, os processos de aquisição do conhecimento assumem um papel de destaque e passam a exigir um profissional crítico, criativo, com capacidade de pensar e de aprender”. As novas tecnologias trazem um novo conceito, uma nova forma de conhecimento com a utilização de bases de dados, informações, comunicação, interação e construção de conteúdos, para planejamentos e busca de conhecimentos, lidando com novos equipamentos e ferramentas tecnológicas.
As pesquisas mais recentes de Borges e Valente (2014 p. 674) enfatizam a importância das tecnologias da informação e comunicação (TIC) em sala de aula. “Acreditamos que as tecnologias da informação e comunicação serão utilizadas nas escolas de maneira mais efetiva a partir do momento em que há uma apropriação dessas tecnologias por aqueles que lá trabalham”. Com base na citação de Borges e Valente (2014) fica clara a necessidade de mudanças no desenvolvimento das aulas, com uma didática interativa na construção dos conceitos.
Dessa forma, podemos entender que o contato do aluno com os recursos tecnológicos em sala de aula, permite maior disponibilidade de informação sobre os recursos e pode contribuir para o processo de aprendizagem de forma significativa em seu desenvolvimento no ambiente escolar.
Às dificuldades no processo de ensino-aprendizagem que os alunos apresentam ao estudar os conceitos matemáticos, Stoica (2015, p.702) traz outra questão: “Em classes tradicionais de Matemática, os estudantes são ensinados pela primeira vez a teoria e, em seguida, eles são convidados a resolver alguns exercícios e problemas”. Esse método de ensino é cansativo, o aluno gosta do novo e quando o professor busca contribuir com as aulas é certo que a aprendizagem só tende a crescer.
Segundo Moreira (2014, p. 10), “os alunos demonstram desprezo pela disciplina, baseado em reclamações constantes entre os professores”. Sendo o professor o mediador do conhecimento, responsável por oferecer condições adequadas e fazer reflexões acerca das dificuldades, aprimorando as metodologias, ele é aquele orientador que pensa as estratégias de ensino que levam o aluno a compreender as questões que envolvem a Matemática e suas utilidades práticas, permitindo que experimente, tome iniciativa e tire suas próprias conclusões reconhecendo erros e acertos.
Sabemos da importância da inserção das tecnologias em sala de aula para favorecer o raciocínio lógico, na socialização, na organização do pensamento e na concentração. O material é necessário para aproximar os alunos dos conceitos trabalhados e auxiliar na resolução de problemas matemáticos. De acordo com Modrow e Silva (2013), no ambiente escolar as TIC são de extrema importância para agregar, contribuir e dividir informações, fortalecendo as práticas pedagógicas modernas.
Ao ministrar as aulas nas turmas do 1º ano do Ensino Médio na cidade Ariquemes/RO, percebemos as dificuldades apresentadas pelos alunos na aprendizagem da Função Polinomial do 2º grau ou função quadrática, na construção do gráfico, no estudo dos coeficientes, a relação entre o sinal do discriminante e o número de raízes, identificação do vértice da parábola relacionando com o valor máximo ou mínimo da função.
A partir disso, foi necessário refletir sobre a forma como esse conteúdo poderia ser ensinado, de maneira a facilitar o entendimento do aluno e proporcioná-los a consolidação da aprendizagem do conteúdo.
É nesse sentido que buscamos apresentar o software GeoGebra como recurso didático no ensino da função polinomial do 2º grau. Ele oferece recurso para dinamizar e enriquecer as atividades, pois por meio de imagens, desenvolve a capacidade de compreensão e a clareza do raciocínio, além de possibilitar maior participação dos alunos em sala de aula.
Metodologia da pesquisa
Para o desenvolvimento deste trabalho, por meio de uma revisão bibliográfica de natureza qualitativa – uma vez que ela permite que o autor se apodere de novas informações e descreva suas ideias com maior clareza - utilizamos artigos científicos e monografias publicados entre 2011 e 2020 na base Google Acadêmico e no portal de Periódicos da Capes.
Conforme Fonseca (2002, p. 32),
a partir do levantamento de referências teóricas já analisadas, e eletrônicos, como livros, artigos científicos, páginas da web sites. Qualquer trabalho científico inicia-se com uma pesquisa bibliográfica, que permite ao pesquisador conhecer o que já estudou sobre o assunto. Existem, porém pesquisas científicas que se baseiam unicamente na pesquisa bibliográfica, procurando referências teóricas publicadas com o objetivo de recolher informações ou conhecimentos prévios sobre o problema a respeito do qual se procura as respostas.
Na realização da pesquisa bibliográfica se utiliza fundamentalmente diversos autores que tratam do tema. Mas o pesquisador deve refletir e escrever sobre o que estudou a partir deles. Godoy (1995, p. 21) afirma que uma pesquisa qualitativa
não se apresenta como uma proposta rigidamente estruturada, ela permite que a imaginação e a criatividade levem os investigadores a propor trabalhos que explorem novos enfoques. Nesse sentido, acreditamos que a pesquisa documental representa uma forma que pode se revestir de um caráter inovador, trazendo contribuições importantes no estudo de alguns temas. Além disso, os documentos normalmente são considerados importantes fontes de dados para outros tipos de estudos qualitativos, merecendo, portanto, atenção especial.
Segundo Creswell (2010, p. 43), a pesquisa qualitativa é “um meio para explorar e para entender o significado que os indivíduos ou os grupos atribuem a um problema social ou humano”. Nesse procedimento, vale realizar um levantamento dos textos selecionados, principalmente de livros e artigos de periódicos ou revista de publicações avulsas, com o objetivo de coletar as informações mais relevantes sobre o tema pesquisado.
Para a seleção dos artigos, realizamos leituras exploratórias de todos os materiais selecionados, como leituras rápidas, com o objetivo de interesse para o trabalho, e leituras seletivas, aprofundadas nas partes de maior interesse.
Para a leitura analítica, com base nos textos selecionados, foram utilizados descritores que tivessem uma relação mais próxima com a temática, entre eles: a função polinomial do 2º grau, a tecnologia, o ensino de Matemática e o software GeoGebra. Embora utilizada a adição de textos ou supressão, ordenamos e sistematizamos as informações contidas nas fontes de forma a obtermos resposta à pesquisa.
Este trabalho foi fundamentado com o objetivo central na revisão bibliográfica, a fim de trazer uma análise crítica a respeito da importância das tecnologias digitais no ambiente escolar, pautando-se em autores referenciais no tema, para assim oferecer um suporte teórico para as escolas começarem a refletir sobre a sua relevância e pensarem formas de implementação, tendo consciência de seu papel no processo educativo.
O presente trabalho foi desenvolvido com 12 alunos do 1º ano do Ensino Médio da Escola Estadual Heitor Villa-Lobos, do município de Ariquemes/RO. À direção e à supervisão da escola, foi comunicado: o objetivo do trabalho, o tempo de duração (4 aulas de 50 minutos) e o local de sua realização (laboratório de Informática, devidamente agendado para que tudo saísse conforme o planejado).
Foram aplicadas quatro sequências didáticas de atividades, elaboradas numa perspectiva investigativa (Ponte, 2009). Para estabelecer uma articulação entre as sequências didáticas, o trabalho foi estruturado em quatro momentos.
No primeiro momento, o objetivo era baixar e apresentar o software GeoGebra, abordando sua história e suas contribuições para o ensino da Matemática. Além disso, exploramos algumas de suas funcionalidades e apresentamos, por exemplo, sua área de trabalho, sua interface e os passos necessários para a construção do gráfico com o apoio do software. Nesse primeiro momento, o produto foi somente analisado, não havendo nenhum registro escrito a respeito.
Em um segundo momento, foi apresentada a função polinomial do 2º grau, com questionários sobre a função quadrática e a análise do comportamento do gráfico quando
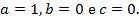
Em seguida, num terceiro momento, foi proposta a análise do gráfico, quando a > 0 e a < 0. Houve a aplicação de um questionário avaliativo sobre as observações durante o desenvolvimento das atividades pelos alunos. Tudo isso foi realizado com a mediação do docente.
No quarto e último momento, identificamos as raízes da função quadrática, os vértices da parábola, o valor máximo ou mínimo no software GeoGebra e, em seguida, os alunos responderam a um questionário elaborado de acordo com os objetivos preestabelecidos das aulas, com a finalidade de colher opiniões sobre o software. Diante da dificuldade argumentativa na escrita dos alunos, realizamos uma discussão oral com o grupo, quando eles expuseram suas observações acerca das questões propostas. Nesse momento, foi fornecida uma folha impressa com o questionário citado. No entanto, a discussão oral foi primordial para nossas considerações; mais uma vez as observações do professor complementam as discussões do trabalho.
Os alunos foram reunidos em um único grupo, em que foi escolhido um aluno redator que ficou responsável por escrever as respostas na folha impressa. A opção por organizar os alunos em grupo buscou privilegiar a interação e discussão entre os participantes, pois conforme afirma Ponte (2009), na investigação matemática “a situação de trabalho em grupo potencializa o surgimento de várias alternativas para a exploração da tarefa”.
As tecnologias da informação e comunicação na Educação e no ensino da Matemática
No decorrer dos séculos, o mundo passou por diversas transformações tecnológicas, levando a sociedade a ter um contato constante com as tecnologias da informação e comunicação (TIC). Essa era digital trouxe consigo mudanças na economia e na sociedade de forma generalizada. Como os educandos estão inseridos nesse contexto social e fazem uso de instrumentos tecnológicos para o lazer, a escola não pode ficar alheia a isso. Ela deve fazer uso dessas tecnologias como instrumentos de ensino-aprendizagem.
Há uma recomendação de estudiosos da área, como Borba e Penteado (2001) e outros, de que as tecnologias sejam difundidas nas escolas brasileiras, a fim de proporcionar uma melhor qualidade no ensino. Muito além do desejo desses pesquisadores, entidades como a Organização das Nações Unidas para a Educação, Ciência e Cultura (Unesco) defendem essa proposta, visto que em seu site Representação da Unesco no Brasil contém a seguinte afirmação:
[A instituição] coopera com o governo brasileiro na promoção de ações de disseminação de TIC nas escolas com o objetivo de melhorar a qualidade do processo ensino-aprendizagem, entendendo que o letramento digital é uma decorrência natural da utilização frequente dessas tecnologias (Unesco, 2017, p. 48).
O trabalho com uso de tecnologias digitais nas práticas educativas vem sendo discutido. Conforme Wolff e Silva (2013), “a utilização de recursos digitais em sala de aula no ensino da Matemática, oferece aos professores uma ampliação nas formas de ensinar, trocas de experiências e conhecimentos”.
O uso das TIC na educação tem como finalidade auxiliar no processo de aprendizagem, pois os recursos permitem ao aluno construir e/ou manipular determinado experimento, fazendo comparações, generalizações e análises, além de permitir o trabalho colaborativo, propondo um ensino de forma dinâmica, que confronta teoria e prática (Wolf; Silva, 2013, p. 2). Para isso, é possível utilizar os recursos tecnológicos como principais aliados do ensino-aprendizagem, em especial na Matemática.
Há uma grande variedade de softwares educacionais livres, de acesso gratuito, que oferecem a possibilidade de estimular o protagonismo dos educandos. No ensino da Matemática, o uso dos softwares propicia grandes vantagens. Por meio da sua utilização adequada, podemos tirar o aluno da situação de sujeito passivo para sujeito ativo no processo de ensino-aprendizagem. Os benefícios alcançados com o uso dos softwares no ensino da Matemática também são apontados por Lopes Júnior (2013, p. 28):
Quando se faz uso de softwares no ensino de matemática, há um avanço nas possibilidades de experimentação, observação, investigação e dedução, etapas do desenvolvimento de teorias matemáticas que são muito importantes para o desenvolvimento dos alunos nessa ciência.
Os documentos oficiais que norteiam a elaboração dos currículos escolares no Brasil já vêm apresentando a necessidade do uso das tecnologias digitais em sala de aula. Segundo os Parâmetros Curriculares Nacionais (PCN),
o uso de recursos tecnológicos em sala de aula tem por finalidade ampliar a visão do aluno sobre determinado conteúdo, visto que, a utilização dessas ferramentas deve atentar para um objetivo pedagógico com planos e metas definidos almejando resultados esperados (Brasil, 1998, p. 56).
Os Parâmetros Curriculares Nacionais para o Ensino Médio (PCNEM) preveem a influência do uso das tecnologias da informação e comunicação (TIC) de forma crítica e reflexiva no contexto escolar.
O impacto da tecnologia, cujo instrumento mais relevante é hoje o computador, exigirá do ensino de Matemática um redirecionamento, sob uma perspectiva curricular, que favoreça o desenvolvimento de habilidades e procedimentos com os quais o indivíduo possa se reconhecer e se orientar nesse mundo do conhecimento em constante movimento (Brasil, 2002, p. 41).
Em 2017, foi publicada a última versão da Base Nacional Comum Curricular (BNCC), atendendo a um dos princípios do Plano Nacional de Educação. Ela pretende implementar um currículo mínimo em todo o país, chamando a atenção para o uso das TIC em sala de aula. Entre as competências gerais da Base, duas estão diretamente relacionadas a esse uso.
Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras e escrita), corporal, visual, sonora e digital – bem como conhecimentos de linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva (Brasil, 2017, p. 539).
A BNCC também indica algumas habilidades relativas à resolução de problemas e previstas nos processos de ensino-aprendizagem:
(EM13MAT302) Construir modelos empregando as funções polinomiais de 1 º ou do 2º graus, para resolver problemas em contexto diversos, com ou sem apoio de tecnologias digitais.
(EM13MAT503) Investigar pontos de máximo ou de mínimo de funções quadráticas em contexto envolvendo superfícies, Matemática financeira ou Cinemática, entre outros, com apoio de tecnologias digitais.
(EM13MAT503) Investigar pontos de máximo ou de mínimo de funções quadráticas em contexto envolvendo superfícies, Matemática financeira ou Cinemática, entre outros, com apoio de tecnologias digitais (Brasil, 2017, p. 539).
Assim sendo, pode-se afirmar que o uso de softwares tem o potencial de minimizar as dificuldades sentidas pelo aluno e, consequentemente, levá-lo a interessar-se pela disciplina, aprendendo Matemática conforme proposto na BNCC. Os softwares ainda podem ser utilizados em conjunto com outros recursos, inclusive com os tradicionais, conforme defende Vieira (2015): “incrementar meios computacionais, integrando-os aos outros recursos tradicionais como quadro e giz, exercícios em folhas impressas etc., a fim de que possa enriquecer a aula, tornando-a mais agradável e interessante”.
Pelas afirmações de Vieira, Lopes Júnior e demais autores estudados, percebe-se que a utilização de recursos tecnológicos no ensino é extremamente relevante, pois desperta o interesse no aluno para o estudo, possibilitando que ele participe de forma mais efetiva e se beneficie. A prática pode ser uma forma de auxiliar na consolidação do aprendizado dos conceitos estudados teoricamente.
No entanto, para que haja um real sucesso no uso efetivo das TIC é fundamental que o professor seja analítico ao adotar recursos tecnológicos como ferramentas de ensino. A mudança não ocorre apenas pelo incremento desses mecanismos de ensino, conforme salienta Gravina (1998): “se almeja-se uma mudança de paradigma para a educação, é necessário ser crítico e cuidadoso neste processo de uso da informática. A informática por si só não garante esta mudança”.
Os softwares educativos podem ser um bom recurso auxiliar para o aluno adquirir os conceitos matemáticos, que regularmente ele não consegue assimilar por intermédio das metodologias convencionais de ensino. Baseado nos pressupostos teóricos apresentados e nos resultados de outras pesquisas, como as de Lopes Júnior (2013) e de Vieira (2015), buscamos aqui evidenciar a importância da tecnologia no ensino da Matemática e, principalmente, investigar quais são as contribuições do software GeoGebra para a compreensão dos conceitos relativos à função polinomial do 2º Grau.
Análise e discussão dos resultados
Neste capítulo, será relatado o resultado da análise das atividades aplicadas e das observações realizadas ao longo da aplicação. Serão pontuados os avanços e as dificuldades apresentadas pelos alunos.
No primeiro momento, aplicamos a atividade 1, com as seguintes orientações:
I - No campo de Entrada digite f(x)=ax²+bx+c, e em seguida aperte “ENTER”;
II - Utilize a ferramenta controle deslizante e crie controles deslizantes para os coeficientes
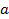 ,
,
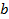 e
e
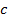 .
.
III – Responda: ao variar o controle deslizante de a, de acordo com o intervalo, e mantendo os controles b e c constantes, o que você observou? Explique.
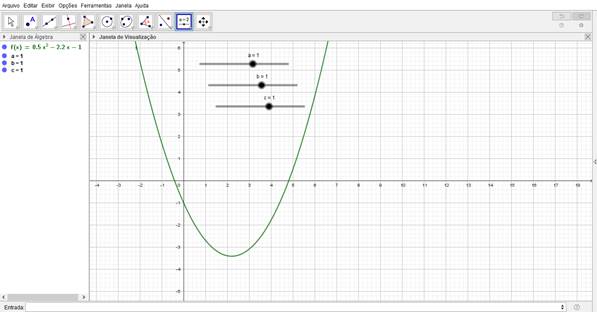
Figura 1: Gráfico da função f(x)=ax²+bx+c
A primeira atividade tinha por objetivo apresentar aos alunos o software GeoGebra e a construção de uma função simples do tipo f(x)=ax²+bx+c, movimentando os controles deslizantes para observar o que aconteceria com os valores de a, b, c.
Pelas observações, afirmamos que os alunos conseguiram ter uma noção básica do software no primeiro contato. Chega-se a essa conclusão, porque ao serem questionados sobre algum conhecimento anterior sobre o software, todos afirmaram que não o conheciam. No entanto, conseguiram usar os comandos e a realizar a construção dos gráficos de funções, conforme orientações. Todos baixaram o programa no laboratório de informática e foi possível observar que fizeram isso com muita facilidade.
Como esperado, os alunos demonstraram desenvoltura em manusear o computador e todos possuíam smartphones, comprovando o argumento de que os educandos observados são indivíduos que fazem uso das novas tecnologias, em decorrência da crescente globalização e se interessam muito por elas. Logo, isso aguçou a curiosidade pelas atividades.
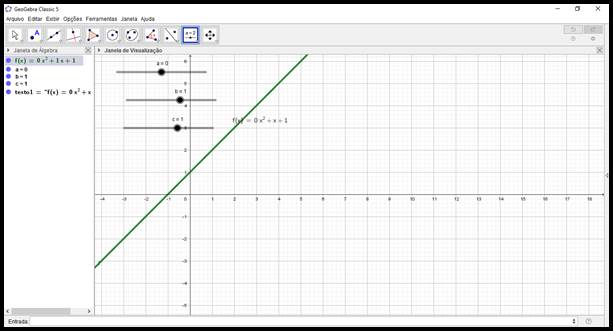
Figura 2: Gráfico da função f(x)=ax²+bx+c, quando
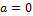 ,
,
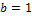 ,
,
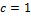
Em seguida, propusemos a atividade 2: analisar no GeoGebra o comportamento do gráfico quando o coeficiente
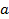 é igual a zero. Os alunos foram questionados sobre o porquê do coeficiente
é igual a zero. Os alunos foram questionados sobre o porquê do coeficiente
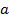 da função Polinomial do 2º grau ser diferente de zero. Observando o gráfico, eles mesmos concluíram que se o coeficiente
da função Polinomial do 2º grau ser diferente de zero. Observando o gráfico, eles mesmos concluíram que se o coeficiente
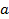 for igual a zero, teremos uma função do 1º grau, conforme a Figura 6.
for igual a zero, teremos uma função do 1º grau, conforme a Figura 6.
A terceira atividade sugeriu a análise do gráfico quando
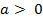 e
e
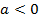 . De acordo com os gráficos abaixo, os alunos puderam observar que aquela que apresenta o coeficiente a positivo tem a concavidade da parábola voltada para cima e aquela que apresenta o coeficiente a negativo tem a concavidade da parábola voltada para baixo.
. De acordo com os gráficos abaixo, os alunos puderam observar que aquela que apresenta o coeficiente a positivo tem a concavidade da parábola voltada para cima e aquela que apresenta o coeficiente a negativo tem a concavidade da parábola voltada para baixo.
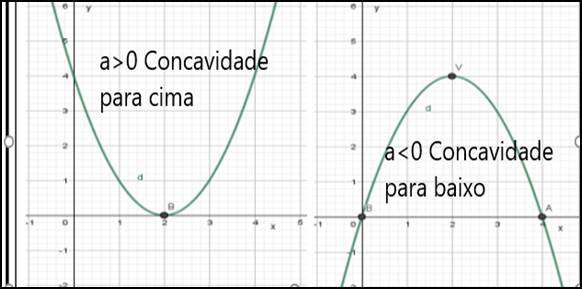
Figura 3: Gráfico da função f(x)=ax²+bx+c, quando
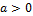 e
e
Roteiro para criação do Gráfico da função quadrática no GeoGebra.
1 - Relacionar número de discriminante com número de raízes. |
2 - Identificar as raízes ou zeros da função quadrática. |
Roteiro:
|
Roteiro:
|
3 - Identificar o vértice da parábola relacionando com o valor máximo ou mínimo da função. |
Roteiro:
|
Atividade 1: Modifique os parâmetros de a, b ou c de forma que o gráfico intercepte o eixo em dois pontos. Qual o sinal do Δ? |
Atividade 2: Fazendo a = 4, b = -4 e c = 2, o que acontece com o gráfico? Qual o sinal do Δ? |
Resposta: |
Resposta: |
Atividade 3: Relacione a primeira coluna com a segunda: (1) Se Δ > 0 (positivo), então ( ) O gráfico não intercepta o eixo x. (2) Se Δ < 0 (negativo), então ( ) O gráfico toca uma única vez o eixo x. (3) Se Δ = 0 (nulo), então ( ) O gráfico intersecta o eixo x em dois lugares distintos. |
Atividade 4: Fazendo a = 2 e b = 0, qual deve ser o valor do coeficiente c para que as raízes sejam:
|
Resposta: |
Resposta: |
Atividade 5: Fazendo a = 2 e b = 0, qual deve ser o valor do coeficiente c para que as raízes sejam:
|
Atividade 6: Fazendo a = -1, b = 1 e c = 2, qual o valor das raízes? |
Resposta: |
Resposta: |
Atividade 7: Altere o valor de “a”, “b” e “c” e verifique se: a) O ponto V será ponto de mínimo se _________________ (a > 0 ou a < 0)? b) O ponto V será ponto de máximo se _________________ (a > 0 ou a < 0)? |
Atividade 8: Fazendo a = -1, b = 2 e c = 4, encontre as coordenadas do vértice e diga se V é o ponto de máximo ou mínimo? Justifique. |
Resposta: |
Resposta: |
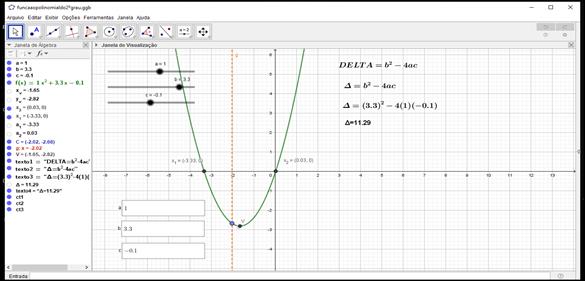
Figura 4: Resultado esperado do gráfico f(x)=ax²+bx+c
Após as aplicações das atividades, finalizando a sequência didática, buscou-se levantar a questão sobre o uso das novas tecnologias em sala de aula. Nesse último momento, fez-se uma análise prévia das respostas ao questionário.
Questionário avaliativo:
1) Você já teve experiências anteriores com as novas tecnologias (computador, software, tablet, smartphone etc.) também chamadas de tecnologia da informação e comunicação (TIC) para aprender Matemática ou alguma outra disciplina?
2) Já conhecia o software GeoGebra?
3) Você achou o software difícil ou fácil de usar? Explique.
4) Como você avalia seus conhecimentos sobre função polinomial do 2º grau antes e depois das atividades envolvendo o GeoGebra?
5) O software te ajudou a entender melhor os conceitos de função, assim como a construção do gráfico e suas raízes?
6) Você recomendaria o software GeoGebra para um amigo? Justifique.

Figura 5: Atividade da Sequência V
Na questão 4 do questionário avaliativo, o aluno tinha que analisar e responder a seguinte pergunta: “Para você, a aula contribuiu para a sua aprendizagem em relação à função polinomial do 2º grau?”. Quanto à avaliação dos conhecimentos, antes e depois da atividade, alunos relataram que previamente sabiam algumas coisas sobre função polinomial do 2º grau, mas, com a realização da atividade no GeoGebra, conseguiram entender bem melhor o conteúdo. Ainda disseram que foi uma excelente experiência e por isso passaram a ter mais conhecimentos. Também salientaram a oportunidade de conhecerem uma ferramenta de ensino que nem sabiam da existência, afirmando que após a participação nas atividades, tudo foi prazeroso e dinâmico.
Nesse ponto, observamos que as atividades atingiram seus objetivos. Isso nos permite dizer que os alunos construíram alguns significados para os conceitos das funções. Percebe-se depois que os alunos que fizeram o gráfico no software GeoGebra, compreenderam melhor o processo pelas observações e os registros. Isso demarca a contribuição para o aprendizado, para a motivação, o interesse e o envolvimento dos alunos. Com relação ao aprendizado, os alunos deram opinião acerca da utilização da tecnologia como metodologia do ensino da Matemática.

Aluno G. S., de 16 anos
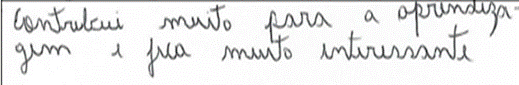
Aluno T. A., de 16 anos

Aluno: M. V., de 16 anos

Aluno P. C., de 17 anos
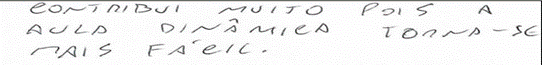
Aluno M. H., de 17 anos

Figura 6: Fragmentos de atividade
Seguindo as atividades, a quarta proposta foi a relação do sinal do discriminante e o número de raízes e o comportamento do gráfico, nesses pontos. Para isso, foram dadas as seguintes orientações:
- Digite na caixa de entrada: delta=b²-4*a*c
- Movimente os seletores de “a”, “b” e “c” na tela.
- Observe o valor do delta e o gráfico.
- Relacione a existência ou não de raízes com sinal do delta.
- Responda: deslizando
- Os valores de a, b, ou c de forma que o gráfico intercepta o eixo em dois pontos. Qual o sinal do ∆?

Figura 7: Fragmentos de atividades
Nessa atividade, o aluno não teve dificuldade em entender visualmente analisando o gráfico da função, pois a parábola intercepta o eixo em dois pontos distintos.
Finalizando as atividades no GeoGebra, propusemos a criação do gráfico e da inserção de dados cujo objetivo era identificar o vértice da parábola, relacionando-o com o valor máximo ou mínimo da função:
- Digite no campo de entrada do GeoGebra: x_v= -b/(2*a)
- Digite no campo de entrada do GeoGebra: y_v=-delta/(4*a)
- Digite no campo de entrada GeoGebra: X= x_v, y_v)
Após a inserção dos dados, os alunos fizeram as atividades propostas no roteiro e foi percebido que os alunos que estiveram presentes em todas as atividades demonstraram mais facilidade em concluir as tarefas.
Da análise preliminar feita, observa-se que os estudantes, além de construírem o gráfico da função solicitada, puderam determinar suas raízes e seu vértice. Na perspectiva da gênese instrumental, à medida que o sujeito continua a manipular o instrumento, constrói novos esquemas que transformam esse instrumento.
Roteiro para criação da figura no GeoGebra:
- Utilize a ferramenta ‘controle deslizante’ e crie os controles deslizantes para os parâmetros a, b, c.
- No campo de entrada digite a expressão:
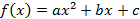
- Digite na caixa de entrada: delta=b²-4*a*c
- Digite na caixa de entrada: x_1=(-b+srqt(delta)) /(2*a)
- Digite na caixa de entrada:x_2=(-b-srqt(delta)) /(2*a)
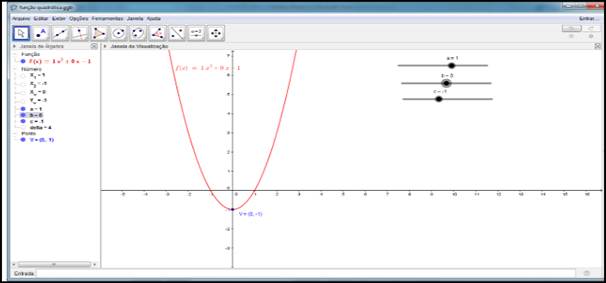
Figura 8: Gráfico feito pelos alunos durante a atividade
Como se pode observar, os alunos responderam de forma pouco fundamentada. Mas afirmaram, oralmente, que havia o interesse. Eles se esforçaram para a realização e para o cumprimento de todas as etapas, mostrando que o uso das ferramentas tecnológicas em sala de aula ocasiona uma aprendizagem significativa.
Conclusão
Para o desenvolvimento deste trabalho, apontamos a importância das tecnologias digitais para o ensino da Matemática. Um recurso que só tem a contribuir com a aprendizagem dos alunos tornado as aulas mais dinâmicas e atrativas, a fim de fugir do ensino tradicional com o uso da lousa.
O uso do software GeoGebra no ensino da função polinomial do 2º grau é muito mais eficaz. Ele leva o aluno a pensar e a aprender a Matemática de forma significativa. O professor consegue despertar no aluno a curiosidade, com o auxílio de atividades interessantes, gerando nele a capacidade de criar ideias.
Dessa forma, como professores no Ensino Fundamental e Médio, sabemos que a função quadrática é um conteúdo muito importante que começa a ser trabalhado em sala de aula muito cedo, servindo de pré-requisito para as diversas áreas do conhecimento matemático.
Os softwares apresentam uma variedade de ferramentas facilitadoras aos educadores matemáticos, permitindo o desenvolvimento de um trabalho que proporcione aos alunos um aprendizado significativo dos conceitos, tornando-os investigadores e competentes na percepção das informações e na compreensão e aplicação dos conceitos matemáticos. É sabido que o software GeoGebra é uma ferramenta que só tem a contribuir com a aprendizagem dos alunos, portanto, se conclui que a inserção das TIC nas aulas é uma forma de auxiliar o aluno no desenvolvimento de atividades diferentes que viabilizam um aprendizado significativo, à medida que o conhecimento é construído de forma interativa e dialógica.
Referências
BITTENCOURT, Patrícia Mello. Utilização do GeoGebra na construção de instrumentos pantógrafo. Dissertação (Mestrado em Matemática em Rede Nacional) - Instituto Nacional de Matemática Pura e Aplicada, Rio de Janeiro, 2014. Acesso em: 21 dez. 2021.
BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e Educação Matemática. 3ª ed. Belo Horizonte: Autêntica, 2001.
BORGES E VALENTE, J. A. Aprendendo para a vida: o uso da informática na Educação Especial. In: FREIRE, Fernanda Maria Pereira; VALENTE, José Armando (org.). Aprendendo para a vida: os computadores na sala de aula. São Paulo: Cortez, 2001.
BRASIL. Ministério da Educação.Base Nacional Comum Curricular. Brasília: MEC/Consed/Undime, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 8 mar. 2022.
BRASIL. Ministério da Educação.Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1998. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf. Acesso em: 8 maio 2022.
BRASIL. Ministério da Educação.Parâmetros Curriculares Nacionais para o Ensino Médio. Brasília: MEC, 2002. http://portal.mec.gov.br/seb/arquivos/pdf/CienciasNatureza.pdf. Acesso em: 30 abr. 2022.
BRASIL. Ministério da Educação. Educação Básica: Pisa 2018 revela baixo desempenho escolar em Leitura, Matemática e Ciências no Brasil. Brasília, 2019. Disponível em: http://portal.mec.gov.br/ultimas-noticias/211-218175739/83191-pisa-2018- revela-baixo-desempenho-escolar-em-leitura-matematica-e-ciencias-no-brasil. Acesso em: 28 jan. 2022.
CRESWELL, J. W. W. Projeto de pesquisa: métodos qualitativo, quantitativo e misto. 2ª ed. Porto Alegre: Bookman, 2010.
DANTAS, Sérgio Carrazedo. O GeoGebra. s.d.
DANTAS, Sérgio Carrazedo. Design, implementação e estudo de uma rede socioprofissional online de professores de Matemática. Tese (Doutorado em Educação Matemática), Universidade Estadual Paulista, Rio Claro, 2016. Disponível em: https://repositorio.unesp.br/handle/11449/136324. Acesso em: 21 fev. 2022.
DANTE, L. R. Matemática: contexto e aplicações. São Paulo: Ática, 2010.
FONSECA, J. J. S. Metodologia da pesquisa científica. Fortaleza: UEC, 2002. Apostila.
GODOY, Arilda Schmidt. Introdução à pesquisa qualitativa e suas possibilidades. RAE - Revista de Administração de Empresas, São Paulo, v. 35, nº 2, p. 57-63, 1995. Disponível em: https://www.scielo.br/pdf/rae/v35n3/a04v35n3.pdf. Acesso em: 30 abr. 2022.
GRAVINA, Maria Alice; SANTA ROSA, Lucila Maria. A aprendizagem da Matemática em ambientes informatizados. Edumatec, Brasília, 1998.
HOHENWARTER, Markus et al. GeoGebra: red de Institutos GeoGebra. Disponível em: https://www.geogebra.org/institutes. Acesso em: 21 jan. 2022.
IEZZI, Gelson et al. Matemática: ciência e aplicações. 9ª ed. São Paulo: Saraiva, 2016.
INSTITUTO GEOGEBRA INTERNACIONAL DE SÃO PAULO (IGISP). GeoGebra. São Paulo: Pontifícia Universidade Católica de São Paulo. s.d. Disponível em: https://www.pucsp.br/geogebrasp/pesquisa_publicacoes.html. Acesso em: 22 fev. 2022.
KENSKI, V. M. Educação e tecnologia: novo ritmo da informação. Campinas: Papirus, 2007.
LOPES JÚNIOR, Geraldo. Geometria dinâmica com o GeoGebra no ensino de algumas funções. Dissertação (Mestrado em Matemática em Rede Nacional) - Universidade Federal de Viçosa, Viçosa, 2013. Disponível em: https://www.locus.ufv.br/bitstream/123456789/5877/1/texto%20completo.pdf. Acesso em: 1 mar. 2022.
MERCADO, L. P. Leopoldo. Formação do docente e novas tecnologias. 2002. Disponível em: http://www.c5.cl/ieinvestiga/actas/ribie98/210M.html. Acesso em: 15 mar. 2022.
MODROW, E. S.; SILVA, M. B. A escola e o uso das TIC: limites e possibilidades. Caderno PDE [on-line], Curitiba, 2013. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2013/2013_uepg_ped_artigo_elizabeth_santanna_modrow.pdf. Acesso em: 24 abr. 2022.
MOREIRA, J. C. A. Os jogos no ensino da Matemática: atividades envolvendo jogos matemáticos no ensino de frações para alunos nas séries finais do Ensino Fundamental.64f. Monografia (Licenciatura em Matemática) - Universidade Estadual de Goiás, Jussara, 2014.
MOULIN, A. P. de Araujo. A utilização do software GeoGebra no processo de aprendizagem da Matemática. ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA (SBEM). Cuiabá, 2019. Disponível em: https://sbemmatogrosso.com.br/eventos/index.php/enem/2019/paper/download/1587/1283. Acesso em: 15 mar. 2022.
NUNES, Sérgio da Costa; SANTOS, Renato Pires do.O construcionismo de Papert na criação de um objeto de aprendizagem e sua avaliação segundo a taxonomia de Bloom. São Paulo, 14 nov. 2013.
ORGANIZAÇÃO DAS NAÇÕES UNIDAS PARA A EDUCAÇÃO, A CIÊNCIA E A CULTURA (UNESCO). TIC na educação. 2017. Disponível em: https://pt.unesco.org/fieldoffice/brasilia/expertise/ict-education-brazil. Acesso em: 22 fev. 2022.
PONTE, João Pedro da. Investigação sobre investigações matemáticas em Portugal. s.d.
PONTE, João Pedro da; BROCARDO, Joana; OLIVEIRA, Hélia. Investigações matemáticas na sala de aula. 2ª ed. Belo Horizonte: Autêntica, 2009.
PROCÓPIO, Madames. O currículo de Matemática do Estado de São Paulo: sugestões de atividades com o uso do GeoGebra. 193f. Dissertação (Mestrado em Educação) – Faculdade de Educação, Pontifícia Universidade Católica de São Paulo, São Paulo, 2011. Disponível em: https://tede2.pucsp.br/handle/handle/10895. Acesso em: 23 jan. 2022.
REIS, Adinilson Marques. Uma proposta dinâmica para o ensino de função afim a partir de erros dos alunos no primeiro ano do Ensino Médio. 167f. Dissertação (Mestrado em Educação) – Pontifícia Universidade Católica de São Paulo, São Paulo, 2011.
SÁ, Adriana Lourenço; MACHADO, Marília Costa. O uso do software GeoGebra no estudo de funções. XIV EVIDOSOL; XI CILTEC on-line. Junho 2017. Disponível em: https://eventos.textolivre.org/moodle/course/view.php?id=12. Acesso em: 15 mar. 2022.
STOICA, A. Using math projects in teaching and learning. Procedia - Social and Behavioral Sciences, v. 180, p. 702-708, 2015.
VIEIRA, Marcelo Luiz. O uso do software Super Logo para o ensino de quadriláteros no 9º ano do Ensino Fundamental. Trabalho de conclusão de curso (Licenciatura em Matemática) - Universidade Federal dos Vales do Jequitinhonha e Mucuri, Teófilo Otoni, 2015.
WOLFF, M. E.; SILVA, D. P. Software GeoGebra no ensino de Matemática. Programa de Desenvolvimento Educacional – PDE, Curitiba, 2013. Disponível em: http://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2013/2013_unicentro_mat_artigo_maria_eliza_wolff.pdf. Acesso em: 5 mar. 2022.
ZUFFI, E. M. O tema ‘funções’ e a linguagem matemática de professores do Ensino Médio: por uma aprendizagem de significados. 307f. Tese (Doutorado em Educação) – Faculdade de Educação, Universidade de São Paulo, São Paulo, 1999.
Publicado em 16 de abril de 2024
Como citar este artigo (ABNT)
SILVA, Roberto Marques da; ROCHA, Joice Stella de Melo. Uma experiência de aplicação do GeoGebra no ensino da função polinomial do 2º grau. Revista Educação Pùblica, Rio de Janeiro, v. 24, nº 13, 16 de abril de 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/13/uma-experiencia-de-aplicacao-do-geogebra-no-ensino-da-funcao-polinomial-do-2-grau
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

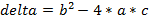
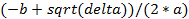
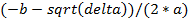
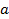 ","b " e "c" na tela.
","b " e "c" na tela. 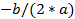
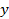 =
=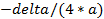
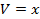 _v, y_v)
_v, y_v) 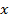 _v, y_v)
_v, y_v) 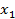 = -1 e
= -1 e
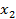 = 1?
= 1?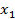 = -1 e
= -1 e
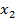 = 1?
= 1?