A resolução de problemas de contagem por jovens e adultos: o uso de conhecimentos prévios e a metodologia de resolução de problemas
Silvane de Sousa Verch
Especialista em Ensino de Matemática para o Ensino Médio (Unipampa), licenciada em Matemática (UFRGS), professora de Matemática da EJA
Leandro Blass
Doutor em Modelagem Computacional (UERJ), professor do Ensino Superior
Everson Jonatha Gomes da Silva
Doutor em Engenharia Mecânica (UFRGS), professor do Ensino Superior
O trabalho apresenta a prática de uma aula inédita para a docente. A aula foi aplicada no componente curricular Matemática Planejada e Aplicada para estudantes da Educação de Jovens e Adultos (EJA) do Ensino Médio durante três anos de um curso oferecido a distância em uma instituição privada. A prática foi realizada presencialmente no polo Porto Alegre/RS. Os estudantes tinham acesso às aulas de Matemática de forma autônoma pela plataforma Moodle (Modular Object-Oriented Dynamic Learning Environment), com fórum de dúvida para contato com a docente.
A autonomia é uma característica importante para o aluno da EaD, pois a flexibilidade dos espaços e tempos, no processo de ensino-aprendizagem, exige que o aluno seja capaz de conduzir seus estudos, organizar-se para tal e possuir maior iniciativa (Bezerra, 2016, p. 67).
A aula inédita tem como tema a resolução de situações-problema de contagem por meio do Princípio Fundamental da Contagem (PFC), com o objetivo de verificar se a metodologia de resolução de problemas (RP) é capaz de facilitar a compreensão de problemas de contagem. A docente utilizou problemas voltados à realidade do mundo do trabalho dos estudantes, fazendo uso de seus conhecimentos prévios. Apresentou as quatro fases da metodologia de RP propostas por Polya (1995) e propôs novos problemas para verificar a potencialização dessa metodologia.
O público da EJA tem um diferencial por já vivenciarem situações que envolvem RP no seu cotidiano, nas quais já se utilizam da Matemática e de outros conhecimentos. Dessa forma, valorizou-se seus conhecimentos prévios, oportunizando, ampliando e aprofundando seus conhecimentos por meio de situações significativas.
A valorização da Matemática construída a partir de experiências cotidianas que muitos jovens e adultos desenvolveram, bem como na reflexão de que uma EJA significativa, para os que agora iniciam ou reiniciam o processo de sistematização formal de ensino, é aquela capaz de valorizar o conhecimento que os alunos trazem para a escola como ponto de partida para novas aprendizagens (Lima; Selva, 2013, p. 235).
Sendo assim, a docente acreditou que seria mais acessível explorar a contagem com situações voltadas ao mundo do trabalho, pois a maioria dos estudantes é trabalhador da indústria e “a aprendizagem contextualizada faz com que o aluno passe a ser ativo no processo de ensino e aprendizagem, visto que levará em consideração os conhecimentos e informações que ele já possui” (Damasceno; Oliveira; Cardoso, 2018, p. 117). Desse modo, há a necessidade de o educador
proporcionar situações para que o aluno desenvolva a habilidade de pensar criativamente com objetivo de enfrentar circunstâncias futuras. Por outro lado, o aluno precisa de dedicação para tornar-se agente da sua aprendizagem, apresentando autonomia para refletir sobre o problema e buscar a solução mais adequada para ele (Paz, 2017, p. 38).
Afinal, ainda existe o problema da descrição
de uma situação onde se procura algo desconhecido e que não se tem previamente nenhum algoritmo que garanta a sua solução. Resolver problema então exige iniciativa, criatividade e conhecimento de estratégias” (Souza; Ohira; Pereira, 2018, p. 379).
Posto isso, a docente proporcionou aos estudantes da EJA situações-problema que os colocassem como agentes ativos.
Metodologia
A metodologia da RP aplicada foi a elaborada por George Polya que considera quatro fases importantes para resolver problemas, tendo em vista que
acontecerá o pior se o estudante atirar-se a fazer cálculos e a traçar figuras sem ter compreendido o problema. É geralmente inútil executar detalhes sem perceber a conexão principal ou sem ter feito uma espécie de plano. Muitos enganos podem ser evitados se, na execução do seu plano, o estudante verificar cada passo. Muitos dos melhores efeitos podem ficar perdidos se ele deixar de reexaminar e de reconsiderar a solução completa (Polya, 1995, p. 4).
As quatro fases propostas por Polya (1995, p. 10) utilizadas nas aulas são representadas na Figura 1.
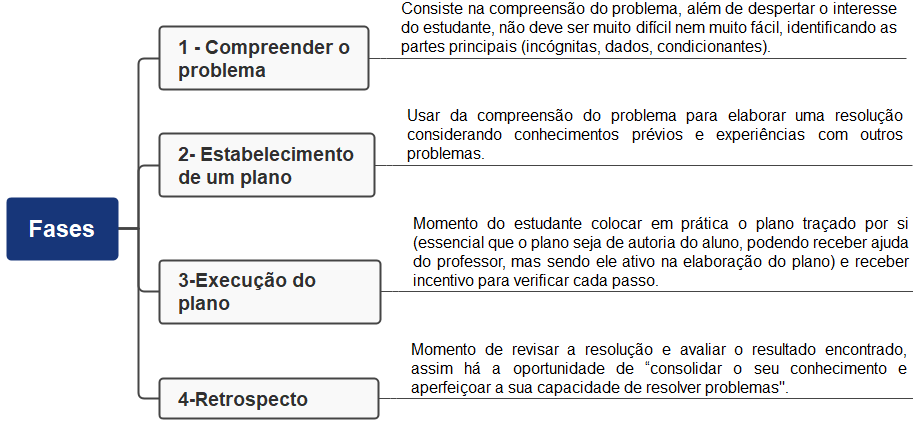
Figura 1: As quatro fases da resolução de problemas
Fonte: Polya, 1995, p. 10.
A cada etapa da aula inédita, os estudantes foram estimulados à leitura, à compreensão, à interpretação e à discussão, tanto individual como coletivamente, proporcionando iniciativa, criatividade e uso dos conhecimentos matemáticos nas RP.
A resolução de problemas é peça central para o ensino de Matemática, pois o pensar e o fazer se mobilizam e se desenvolvem quando o indivíduo está engajado ativamente no enfrentamento de desafios. Essa competência não se desenvolve quando propomos apenas exercícios de aplicação dos conceitos e técnicas matemáticos. Na resolução de problemas, o tratamento de situações complexas e diversificadas oferece ao aluno a oportunidade de pensar por si mesmo, construir estratégias de resolução e argumentações, relacionar diferentes conhecimentos e, enfim, perseverar na busca da solução. E, para isso, os desafios devem ser reais e fazer sentido (Brasil, 2000, p. 112-113).
Portanto, um dos objetivos da aula inédita foi proporcionar aos estudantes a oportunidade de aplicar e ampliar seus conhecimentos matemáticos por meio da metodologia de RP. Gomes e Stahl (2020, p. 303) afirmam que “um dos aspectos positivos apresentados pela aplicação da RP foi a contextualização do conteúdo, por meio da qual os conceitos e teorias da disciplina passaram a fazer mais sentido para os alunos”. A pesquisa de Paz destacou que
a metodologia de resolução de problemas apresenta-se como uma excelente estratégia para se ensinar Matemática. Essa prática proporciona um ambiente favorável para a aprendizagem dos alunos, uma vez que ao lidar com situações contextualizadas, traz questões da realidade e parte do real para o teórico, levando o aluno a fazer reflexões e questionamentos sobre os problemas, através de circunstâncias desafiadoras que estimulam os alunos a buscar soluções, desenvolvendo a autonomia e, inclusive, fazendo com que percebam que uma mesma metodologia e raciocínio são aplicáveis em questões semelhantes, transformando-os, dessa forma, nos agentes responsáveis pela construção dos seus conhecimentos (Paz, 2017, p. 98).
O plano de aula da aula inédita
Inicialmente, todos os participantes assinaram o termo de consentimento livre e esclarecido (TCLE). A pesquisa é caracterizada como descritiva, com abordagem quali-quantitativa.
São inúmeros os estudos que podem ser classificados sob este título e uma de suas características mais significativas está na utilização de técnicas padronizadas de coleta de dados, tais como o questionário e a observação sistemática (Gil, 2002, p. 42).
Qualitativamente, “é uma pesquisa interpretativa, com o investigador geralmente envolvido em uma experiência sustentada e intensiva com os participantes” (Creswell, 2007, p. 188), embasada pelos questionários e pela qualidade das respostas às propostas. Quantitativamente, “são estimativas numéricas de valores da população baseados em dados coletados em amostras” (Creswell, 2007, p. 120), quando, no questionário final, contém perguntas a serem atribuídas notas e posteriormente são calculadas as médias.
O plano de aula foi dividido em quatro partes (questionário inicial, resolução de problemas – em duas etapas – e questionário final), com os objetivos de:
- Experimentar a resolução de situação-problema, que envolve o PFC, utilizando-se de conhecimentos prévios e experiências de vida.
- Aplicar a metodologia de resolução de problemas.
- Identificar quais conhecimentos matemáticos estão sendo utilizados na resolução das situações-problema sobre PFC.
- Articular, em grupo, a resolução de situações-problema de PFC, em duas etapas.
- Avaliar o desempenho na resolução de situação-problema após exposição de práticas na resolução de situações-problema que envolvam PFC.
Coleta de dados e a descrição da sequência didática
A Figura 2 representa como foi realizada a coleta de dados e a sequência didática.

Figura 2: Coleta de dados e sequência didática
Seguem os quadros, representando cada parte da sequência didática.
Quadro 1: Questionário inicial
- Nome:
- Idade:
- Fase:
- Quanto tempo você ficou longe dos estudos?
- Você usa Matemática no seu dia a dia? Dê um exemplo.
- Você prefere questões de Matemática que envolvam resolução de problemas ou exercícios de fixação? Explique.
- Você acredita que com seus conhecimentos prévios e sua experiência de vida, você consegue resolver questões que envolvem contagens? Explique.
- Você sabe o que é o Princípio Fundamental da Contagem ou Princípio Multiplicativo? Explique.
- Você conhece/já ouviu falar de Permutação, Arranjo e Combinação? Explique.
- Tente resolver esta situação-problema sobre contagem:
Uma lanchonete no centro da cidade está com uma promoção de lanche a um preço único e super atrativo. O cliente pode escolher um entre três opções de sanduíches: hambúrguer, torrada e cachorro-quente, e uma entre duas opções de bebidas: suco de laranja ou guaraná.
Considerando as opções oferecidas, de quantas maneiras um cliente pode escolher o seu lanche?
- Você conseguiu resolver a questão de contagem? Se sim, diga quais conhecimentos matemáticos você utilizou. Se não, diga qual foi sua dificuldade.
- Você acredita que se resolvesse a questão em grupo, discutindo as ideias com seus colegas, poderia se sair melhor?
Quadro 2: Situações-problema - Etapa I
Grupo 1
Uma fábrica lançou quatro novos modelos de camisetas. Kits para venda serão montados com quatro peças, podendo haver repetição de modelo. Quantos kits diferentes podem ser montados com esses quatro modelos?
Grupo 2
Uma fábrica lançou quatro novos modelos de camisetas. Kits com uma peça de cada modelo deverão ser montados para venda. Quantos kits podem ser montados com esses quatro modelos?
Grupo 3
Em uma reunião de setor, quatro funcionários estavam presentes e havia seis cadeiras disponíveis para serem usadas. Considerando que cada pessoa ocupou uma cadeira, de quantas formas distintas esses quatro funcionários puderam sentar-se?
Grupo 4
Uma loja quer liquidar o seu estoque de canecas personalizadas. Existem cinco modelos diferentes de canecas. Para tanto, um funcionário lançou a ideia de montar um kit com três dessas canecas, podendo haver repetição de modelo. Quantos kits diferentes podem ser montados com esses cinco modelos?
Grupo 5
Uma loja quer liquidar o seu estoque de canecas personalizadas. Existem cinco modelos diferentes dessas canecas. Para tanto, um funcionário lançou a ideia de montar um kit com três canecas distintas. Quantos kits diferentes podem ser montados com esses cinco modelos?
Grupo 6
Uma indústria têxtil produziu uma estampa geométrica com seis espaços para receber cores. Acontece que para essa produção há somente quatro cores disponíveis: verde, preto, branco, amarelo. Quantas estampas contêm apenas duas cores?
Grupo 7
Uma indústria têxtil produziu uma estampa geométrica com seis espaços para receber cores. Acontece que para esta produção há somente quatro cores disponíveis: verde, preto, branco, amarelo. Em quantas estampas as cores verde e amarelo aparecem uma única vez?
Quadro 3: Situações-problema - Etapa II
Grupo 1
De uma equipe formada por oito funcionários, quatro serão chamados para representar a equipe em um projeto lançado pela diretoria da empresa em que trabalham. De quantas maneiras diferentes quatro de oito funcionários podem ser chamados para esse projeto?
Grupo 2
Cláudia, Jeferson, Caio, Fabíola, Rodrigo e Michele são colegas de trabalho. Eles estão na linha de produção de determinado produto. Os três primeiros que atingirem a meta ganharão uma bonificação. De quantos modos diferentes podemos ter os três primeiros colocados se Fabíola sempre atinge a meta primeiro?
Grupo 3
Cláudia, Jeferson, Caio, Fabíola, Rodrigo e Michele são colegas de trabalho. De quantas formas diferentes um grupo com quatro deles pode ser formado, considerando que Jeferson é um integrante desse grupo?
Grupo 4
Uma indústria tem dez equipes participando do lançamento de um novo produto. Cada equipe deve criar um novo produto e apresentar para diretoria e gerentes. Serão premiados os três primeiros lugares, e o primeiro colocado terá seu produto lançado. De quantas formas diferentes podemos obter a colocação dos premiados?
Grupo 5
Uma indústria têxtil produziu uma estampa geométrica com seis espaços para receber cores. Acontece que para essa produção há somente quatro cores disponíveis: verde, preto, branco, amarelo. Quantas estampas podem ser produzidas?
Grupo 6
José irá montar um kit de brindes para ser sorteado no Natal entre os funcionários de uma empresa. Ele tem à disposição três títulos de livro, quatro modelos de caneta, oito tipos de hidratante para mãos e dois modelos de agenda. De quantas formas diferentes José pode montar esse kit?
Grupo 7
Dentre dez funcionários que compõem a Cipa, três irão representar a comissão em uma capacitação. Quantos trios poderão ser formados?
Quadro 4: Questionário final
- Nome:
- Qual sua opinião sobre a aula de hoje? Atribua uma nota de 1 a 10: __
- Quais conhecimentos matemáticos foram usados na aula de hoje?
- Com as questões resolvidas hoje, você acredita que ampliou os seus conhecimentos matemáticos? Explique.
- Você compreendeu o Princípio Fundamental da Contagem? Explique.
- Você acredita que poderá aplicar os conhecimentos de hoje em alguma situação do seu cotidiano? Dê um exemplo.
- Você acredita que os problemas ajudaram na sua compreensão do conteúdo? Atribua uma nota de 1 a 10: ________
- O método de resolução de problemas permitiu que desenvolvesse o interesse em aprender? Atribua uma nota de 1 a 10: ________
- O uso dos problemas pode ser considerado uma abordagem que vincula exemplos práticos? Atribua uma nota de 1 a 10: ________
- Você mudou de opinião sobre o tipo de questões de Matemática (prefere resolução de problemas ou exercícios de fixação)? Explique.
- Tente resolver esta situação-problema sobre contagem:
Um grupo de 30 empreendedores deve selecionar três membros para formar uma comissão que irá representar o grupo em uma feira econômica. Quantas comissões distintas podem ser formadas? - Você conseguiu resolver a situação-problema acima? Se sim, diga como a aula de hoje lhe ajudou na resolução. Se não, diga qual foi a sua dificuldade para a resolução da questão.
- Nas atividades realizadas hoje, você preferiu resolver as questões individualmente ou em grupo? Explique.
A aula inédita e os resultados
A aula deveria começar às 8h, com a presença de 35 estudantes da EJA do Ensino Médio, segundo informações do polo. Iniciou-se por volta das 8h30min, com dez estudantes (passando o planejamento para formação de duplas), sendo um estudante do Ensino Fundamental.
A docente utilizou uma apresentação em PowerPoint como diretriz para a aula inédita, realizando sua apresentação e exposição dos objetivos da prática. Ela se colocou à disposição para auxiliar em todas as partes da aula e solicitou o consentimento por meio do TCLE.
Os estudantes apresentaram dificuldade em preencher os dados de identificação nas folhas em cada parte da aula, como será exposto mais adiante, assim como foi observada grande dificuldade de compreensão e interpretação tanto das perguntas dos questionários como das situações-problema propostas.
Análise do questionário inicial
As primeiras perguntas do questionário inicial foram para a identificação dos estudantes, em que preencheram nome e fase do curso da EJA (ocultos durante todo o trabalho aqui apresentado), a idade (que correspondeu à faixa etária de 18 a 63 anos, com média de 35,2 anos) e tempo de afastamento da sala de aula formal (que foi de um a 22 anos, com média de 10,6 anos).
Nas Figuras 3 e 4, visualizamos a dificuldade de compreensão e de interpretação das perguntas, assim como a grafia e a ortografia.

Figura 3: Uso da Matemática pelo estudante B

Figura 4: Uso da Matemática pelo estudante G
Sobre a preferência por questões de resolução de problemas ou exercícios de fixação, a metade prefere exercícios de fixação (por parecer mais prático) e outros preferem a resolução de problemas (por parecer mais interessante ou exercitar o pensamento).
Quando questionados sobre a resolução de questões que envolvem contagem, utilizando seus conhecimentos prévios e suas experiências de vida, a maioria dos estudantes respondeu que conseguia resolver esse tipo de problema, mas quando perguntados se sabiam o que é o PFC ou o Princípio da Multiplicativo, oito estudantes afirmaram não saber do que se tratava.

Figura 5: Sobre permutação, arranjo e combinação pelo estudante I
Claramente se observa uma distorção ou uma dificuldade de interpretação pelos estudantes, conforme Figura 6 e 7, se evidenciam as próximas análises e a resolução da situação-problema que foi utilizada para avaliação diagnóstica. Os estudantes deveriam responder utilizando seus conhecimentos prévios e experiências de vida, individualmente, o que não aconteceu integralmente, pois alguns estudantes discutiram em dupla ou em grupo.

Figura 6: Situação-problema etapa I pelo estudante C

Figura 7: Sobre a resolução da situação-problema pelo estudante D
Por último, os estudantes argumentaram sobre a discussão em grupo como possibilidade de melhor entendimento e resolução de problemas. Oito estudantes afirmaram que se sairiam melhor e dois disseram que dependeria.
Após todos concluírem, a docente expôs a resolução da situação-problema utilizando a metodologia de RP de Polya, conforme a sequência de ilustrações abaixo.

Figura 8: Metodologia de resolução de problemas: Fase 1

Figura 9: Metodologia de resolução de problemas: Fase 2
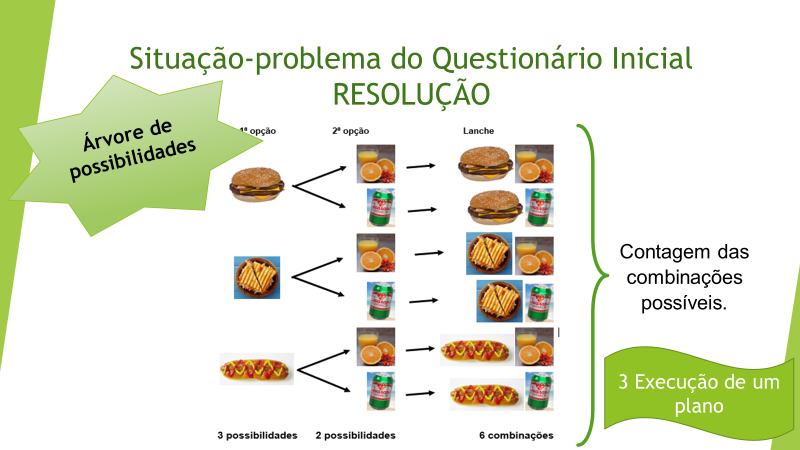
Figura 10: Metodologia de resolução de problemas: Fase 3
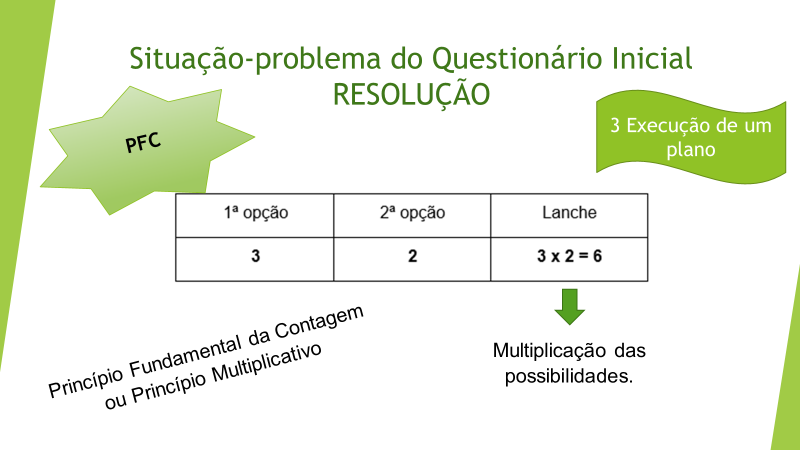
Figura 11: Metodologia de resolução de problemas: Fase 3

Figura 12: Metodologia de resolução de problemas: Fase 4
Os estudantes demonstraram maior entendimento após a exposição e a explicação. A docente ressaltou a importância de compreender e interpretar o que está sendo solicitado.
Análise de resolução de problemas - Etapa I
Seguindo com a sequência didática, a metodologia de RP ficou exposta no quadro. A docente ressaltou o seu uso, assim como estimulou a calma e a discussão em dupla. No preenchimento dos dados com os nomes dos participantes (que seria em grupo de sete componentes e, agora, dupla), os estudantes apresentaram dificuldade. Uma estudante argumentou que colocou o nome na linha 7 por não ter a linha 8 (se referindo à fase 8 que está cursando). Em outra dupla, os componentes colocaram os nomes na mesma linha. A docente circulou entre as duplas participando das discussões para a resolução das situações-problema. Apenas uma dupla acertou a RP, com ajuda da docente. As demais duplas apenas realizaram a multiplicação dos dados numéricos constantes nas situações, em que se observou a dificuldade de compreensão e interpretação.

Figura 13: Resolução de situações-problema - Etapa I: Dupla 3
Análise da resolução de problemas - Etapa II
Ao propor novas situações-problema para resolução, a docente as circulou para as auxiliar, mas dessa vez duas duplas acertaram a resolução, uma dupla desistiu e duas não conseguiram chegar ao resultado correto.

Figura 14: Resolução de situações-problema - Etapa II: Dupla 2

Figura 15: Resolução de situações-problema - Etapa II: Dupla 5
Nessas imagens, percebemos as estratégias usadas para a resolução dos problemas. As demais duplas que tentaram, não mostraram a linha correta de raciocínio, apenas o resultado numérico. De qualquer forma, houve uma evolução, tanto na compreensão como na interpretação.
Análise do questionário final
Referente à opinião dos estudantes sobre a aula, as notas atribuídas ficaram entre oito e dez, com uma média de 9,6, o que representa terem gostado da aula inédita. Sobre os conhecimentos matemáticos usados, a docente esperava algumas respostas citando a multiplicação, operações básicas utilizadas em todas as resoluções, mas apenas três estudantes as citaram. A maioria apontou questões de problema, contagem, permutação, arranjo, combinação e a metodologia de RP.

Figura 16: Conhecimentos usados na aula inédita pelo estudante H
Como pode ser visto (Figura 16), a docente atingiu um objetivo que não estava traçado para a aula inédita e que se faz presente em todas as suas atuações: preparar o estudante para o mundo, a fim de que se torne um cidadão pensante. Um alento nessa jornada docente.
Alguns estudantes afirmaram não terem ampliado seus conhecimentos matemáticos com a aula inédita, mas outros acreditam que conseguiram ampliar.
Metade dos estudantes afirmou que compreendeu o PFC, como escreve o estudante E: “Achei um pouco difícil, pois varia muito, de um exemplo para o outro, mas consegui aprender”. Os demais não compreenderam, compreenderam pouco ou não responderam à pergunta.
Um total de oito alunos respondeu que poderia aplicar os conhecimentos em alguma situação do seu cotidiano. Talvez não tenha ficado muito clara a aplicação, tendo em vista o exemplo citado pelo estudante F, conforme a Figura 17.

Figura 17: Aplicação dos conhecimentos matemáticos com a aula inédita pelo estudante F
Referente às informações quantitativas, presentes no questionário final do Quadro 4, a questão 7 teve média de 7,7, pois os estudantes acreditam que a RP os ajudou na compreensão das atividades. A questão 8 apresentou média de 7,9 e é possível vislumbrar que os estudantes mostraram maior interesse em aprender, praticando o método de RP. Os estudantes apontaram, com uma média de 7,7, para a questão 9, mostrando que o uso dos problemas é um bom caminho para exemplos práticos.
Quando novamente perguntados sobre o tipo de questão de Matemática que tinham preferência (resolução de problemas ou exercício de fixação), três estudantes seguiram preferindo os exercícios de fixação, cinco preferiram a resolução de problemas (com dois novos estudantes) e dois seguiram sem responder.
No questionário final, também havia uma situação-problema para ser resolvida individualmente para uma análise posterior do desenvolvimento da aprendizagem, mas novamente os estudantes discutiram entre si sobre o problema proposto. Nenhum estudante acertou a resolução; quatro não responderam, cinco resolveram incorretamente e um estudante não finalizou a resolução, mas estava no caminho certo.

Figura 18: Situação-problema - Etapa II pelo estudante C
Sobre a influência da aula para a resolução do problema proposto, quatro estudantes reconheceram não conseguir resolver, dois não responderam e dois disseram tentar resolver, justificando ser “um pouco difícil trabalhar com números exatos, faz com que se perdemos, se multiplicação divisão”, conforme cita o estudante E. Já o estudante H ressaltou a serenidade da docente na explicação.
Quanto ao trabalho individual ou em dupla, um não respondeu adequadamente, três preferem o trabalho individual e seis preferem em grupo.
Após recolhimento dos questionários, a docente apresentou a resolução da situação-problema (de forma análoga à resolução da situação-problema do questionário inicial).
Conclusão
A BNCC traz como habilidade a ser desenvolvida a RP de contagem com diferentes estratégias: resolver problemas de contagem por meio do princípio multiplicativo recorrendo a estratégias diversas. Sendo assim, ao longo do texto foram apresentadas análises da aula inédita aplicada, quando é possível perceber que os estudantes não a desenvolveram plenamente, pois concluíram a aula com dificuldades em resolver problemas de contagem. Poucos conseguiram usar do princípio multiplicativo (como pode ser visto na Figura 15) ou no diagrama de árvore (Figura 14).
O fato de os estudantes não terem resolvido as situações-problema de forma individual, utilizando de seus conhecimentos prévios, já mostrava a fragilidade deles em acreditar em si e as dificuldades que teriam para refletir sobre os problemas propostos. A metodologia de RP (compreensão, plano, execução e retrospecto), usada como meio de verificar se facilitaria a compreensão dos problemas de contagem com situações-problema voltadas à realidade do mundo de trabalho dos estudantes, não foi eficaz como se esperava, assim como a articulação da resolução em dupla não foi o suficiente para que houvesse um aproveitamento maior da prática, apesar da maioria argumentar preferir trabalhar em dupla, ou grupo, para discutir os problemas.
A docente acredita que um planejamento explorando unicamente problemas de contagem, sem trabalhar as nuances (permutação, arranjo e combinação) poderia surtir melhor efeito. Como a prática para aula inédita foi apenas um encontro, talvez uma sequência de encontros poderia ser melhor, já que esses estudantes da EJA não têm aulas de Matemática presencialmente (o que os afasta da prática com mediação, como proposto na aula inédita). A dificuldade de compreensão e interpretação se mostrou desde o primeiro problema apresentado, logo o contexto das situações-problema propostas poderiam ser os “mais tradicionais” (como, por exemplo, placas de trânsito, cartões de loteria etc.) ao invés de buscar o contexto do mundo do trabalho. As figuras, especialmente as 5 e 6, mostram as dificuldades na escrita, na compreensão, na interpretação e na organização do pensamento.
Todavia, os estudantes apontaram que o uso dos problemas e o método de RP, colabora para a evolução da compreensão do conteúdo, para o interesse em aprender e para a vinculação com exemplos práticos diante da análise quantitativa.
Nota-se progresso dos estudantes no tema proposto neste trabalho, dessa forma, a docente acredita que a pesquisa pode ter continuidade, com alterações no seu planejamento.
Referências
BEZERRA, Ana Lucia da Silva. Educação de Jovens e Adultos na modalidade a distância: contribuições e desafios na perspectiva do aluno. Dissertação (Mestrado em Educação) - Centro de Ciências da Educação, Universidade Federal de Santa Catarina, Florianópolis, 2016. Disponível em: https://repositorio.ufsc.br/xmlui/handle/123456789/174902. Acesso em: 8 nov. 2022.
BRASIL. Ministério da Educação. Parâmetros Curriculares Nacionais: PCN+ Ensino Médio - Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais. Brasília: MEC, 2000. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/CienciasNatureza.pdf. Acesso em: 14 out. 2022.
CRESWELL, John W. Projeto de pesquisa: métodos qualitativo, quantitativo e misto. Trad. Luciana de Oliveira da Rocha. 2ª ed. Porto Alegre: Artmed, 2007.
DAMASCENO, Adriana de Assis; OLIVEIRA, Guilherme Saramago de; CARDOSO, Márcia Regina Gonçalves. O ensino de Matemática na Educação de Jovens e Adultos: a importância da contextualização. Cadernos da Fucamp, v. 17, n° 29, p. 112-124, 2018. Disponível em: https://revistas.fucamp.edu.br/index.php/cadernos/article/view/1347. Acesso em: 23 ago. 2022.
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. 4ª ed. São Paulo: Atlas, 2002.
GOMES, Diego Monteiro Gomes; STAHL, Nilson Sergio Peres. A resolução de problemas no ensino de cálculo diferencial e integral nos cursos de Engenharia: uma experiência. Revista Thema, v. 17, n° 2, p. 294-308, 2020. Disponível em: https://doi.org/10.15536/thema.V17.2020.294-308.1664. Acesso em: 18 ago. 2022.
LIMA, Izauriana Borges; SELVA, Ana Coêlho Vieira. Jovens e adultos construindo e interpretando gráficos. Bolema - Boletim de Educação Matemática [online], v. 27, n° 45, p. 233-253, jul. 2013. Disponível em: https://doi.org/10.1590/S0103-636X2013000100012. Acesso em: 2 ago. 2022.
PAZ, Vanessa Prado Beraldo da. O princípio fundamental da contagem através da metodologia de resolução de problemas, com foco nas questões da Olimpíada Brasileira de Matemática das Escolas Públicas. Dissertação (Mestrado Profissional) – Instituto de Biociências, Letras e Ciências Exatas, Universidade Estadual Paulista “Júlio de Mesquita Filho”, São José do Rio Preto, 2017.
POLYA, George. A arte de resolver problemas: um novo aspecto do método matemático. Trad. e adapt. Heitor Lisboa de Araújo. 2ª reimpr. Rio de Janeiro: Interciência, 1995. Disponível em: http://im.ufrj.br/~nedir/disciplinas-Pagina/Polya-Arte_Resolver_Problemas.pdf. Acesso em: 29 set. 2022.
SOUZA, Arnold Vinicius Prado; OHIRA, Marcio Akio; PEREIRA, Ana Lucia. A arte de resolver problemas no ensino da Matemática. Revista Valore, v. 3, p. 376-389, dez. 2018. Disponível em: https://revistavalore.emnuvens.com.br/valore/article/view/180. Acesso em: 25 ago. 2022.
Publicado em 04 de junho de 2024
Como citar este artigo (ABNT)
VERCH, Silvane de Sousa; BLASS, Leandro; SILVA, Everson Jonatha Gomes da. A resolução de problemas de contagem por jovens e adultos: o uso de conhecimentos prévios e a metodologia de resolução de problemas. Revista Educação Pública, Rio de Janeiro, v. 24, nº 19, 4 de junho de 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/19/a-resolucao-de-problemas-de-contagem-por-jovens-e-adultos-o-uso-de-conhecimentos-previos-e-a-metodologia-de-resolucao-de-problemas
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

