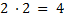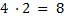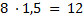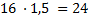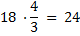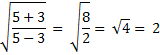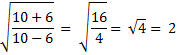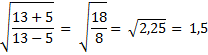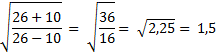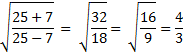Uma nova perspectiva para resolver problemas envolvendo triângulos retângulos

A Geometria é uma das áreas da Matemática que está presente no cotidiano das pessoas e, muitas vezes, não é vista ou notada. No entanto, vemos formas geométricas em lugares diferentes.

Entre todas as formas geométricas conhecidas, uma em particular tem intrigado os matemáticos desde a Antiguidade. Estamos falando do triângulo. É uma figura que apresenta rigidez e é mais simples, podendo assumir diversas formas, dependendo do contexto. Mas um desses triângulos é peculiar, pois para ele há muitas aplicações, fórmulas e teoremas: o triângulo retângulo. Segundo Saikia (2015), o teorema de Pitágoras é um dos resultados mais conhecidos e mundialmente famosos na Geometria do triângulo.

Antes de iniciar a apresentação da nova perspectiva, façamos uma rápida viagem no tempo a fim de conhecer um pouco mais sobre Pitágoras, o Teorema e suas provas.

Um pouco sobre Pitágoras e seu Teorema

Qualquer estudante conhece, ou pelo menos já ouviu falar, do matemático grego Pitágoras. Segundo Ratner (2009), o Teorema de Pitágoras é sem dúvida a afirmação mais famosa (e importante) da Matemática. Segundo o autor, ela pode ser classificada entre as cinco mais belas. O autor afirma que

existem mais de 371 provas do Teorema de Pitágoras originalmente coletadas por um excêntrico professor de Matemática, que as colocou em um livro de 1927, que inclui as de Einstein, de 12 anos, Leonardo da Vinci (mestre em todas as disciplinas) e o presidente da Estados Unidos James A. Garfield (Ratner, 2009, p. 230).

Além do famoso Teorema, Pitágoras é creditado por definir as relações acústicas entre cordas de comprimento proporcional. Assim, segundo Ratner (2009), a maior e mais importante conquista da chamada escola de Pitágoras foi a descoberta de que a diagonal de um quadrado não é um múltiplo racional de seu lado. Isso prova a existência de números irracionais, fato esse que gerou grande perturbação entre os pitagóricos.

Atualmente, o Teorema de Pitágoras é visto como a seguinte equação algébrica, a² = b² + c²; mas Pitágoras não via dessa forma, já que Pitágoras era um geômetra. Ele via isso como uma afirmação geométrica sobre áreas. Foi somente por volta de 1600 d.C. que o teorema assumiu sua forma algébrica atual.

O Teorema, na perspectiva de Pitágoras, é expresso em termos de área da seguinte forma: “Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa (o lado oposto ao ângulo reto) é igual à soma das áreas dos quadrados cujos lados são as duas pernas (os dois lados que se encontram em um ângulo reto)” (Ratner, 2009, p. 233). Em resumo, temos: o quadrado da hipotenusa de um triângulo retângulo é igual à soma dos quadrados dos outros dois lados.

A nova perspectiva

Antes de falarmos sobre a nova perspectiva, precisamos destacar alguns pontos importantes. Lopes (2017, p. 1) afirma que nas “diversas atividades desenvolvidas em sala de aula, desde a Educação Infantil, o aluno é levado a tomar decisões (escolher), diante de diversas possibilidades”.

Ao trabalhar na área de Ciências Exatas, a modelagem matemática torna-se uma ferramenta eficaz na tomada de decisão, pois permite uma melhor visualização do problema. Dessa forma, diante de um problema real, podemos representá-lo por um modelo matemático cuja resolução seja possível (Lopes, 2017). Polya aconselha:

A primeira coisa a fazer com um problema é entendê-lo bem; quem entende mal, entende mal. Precisamos distinguir claramente o objetivo que queremos alcançar: Pense no fim antes de começar. [...] Se o objetivo não estiver claro em nossa mente, podemos facilmente nos desviar do problema e abandoná-lo (Polya, 1957, p. 140).

Lopes (2017) aponta que, dentro da sala de aula, temos que desenvolver com os alunos as etapas de resolução de problemas apresentadas por Polya.

Para agrupar convenientemente as questões e sugestões da nossa lista, iremos distinguir quatro fases de trabalho. Primeiro, temos que entender o problema, temos que entender o que realmente é necessário. Segundo, temos que ver como os vários itens estão inter-relacionados, como o desconhecido está ligado aos dados, para ter a ideia de resolução, para estabelecer um plano. Em terceiro lugar, executamos nosso plano. Em quarto lugar, olhamos para nossa resolução concluída, revisando-a e discutindo-a (Polya, 1957, p. 3-4).

Portanto, uma vez definido o objetivo, o primeiro passo para a resolução de um problema é estruturá-lo a partir de um modelo matemático adequado e, a partir daí, iniciar o processo de obtenção da melhor solução dentre as possíveis, tendo o cuidado de verificar se o modelo está representando o problema.

Gotea (2017) mostra, em seu artigo, algumas provas do Teorema de Pitágoras para os lados e para as diagonais de um polígono inscrito em um semicírculo, tendo como diâmetro um dos lados do polígono, não abordando assim uma perspectiva semelhante à que consideramos apresentar a seguir.

Pagiling (2019) diz que alunos reflexivos escrevem as soluções detalhadamente e fazem uso de diferentes representações para promover a resolução do problema do Teorema de Pitágoras e, segundo ele, “eles usam muito tempo para resolver problemas, mas as soluções são escritas com precisão” (Pagiling, 2019, p. 5). Os alunos considerados impulsivos “usam pouco tempo para resolver problemas, mas as respostas escritas são menos precisas” (Pagiling, 2019, p. 5).

Feita essa afirmação, vamos analisar o seguinte problema, sobre a aplicação do Teorema de Pitágoras: um raio laser foi lançado do alto de um prédio, atingindo o solo em um ponto a 18 metros da base do prédio e, sabendo que o comprimento do raio é 30 metros, calcule a altura do prédio.

Aparentemente, trata-se de um problema simples. Quando dedicamos algum tempo a resolvê-lo, vemos duas formas triviais de resolvê-lo:

1. A primeira usando o Teorema de Pitágoras onde:
1. 30² = x² + 18² ⇒ x² = 30² − 18² ⇒ x² = 900 − 324 = 576 ⇒ x = 24
2. A segunda foi por semelhança de triângulos, pois o triângulo formado é semelhante ao triângulo (3,4,5), ou seja:
1. (18, x, 30) = 6 · (3, 4, 5), com isso x = 6 · 4 = 24.

Porém, conseguimos perceber que existe um outro padrão, muito escondido, nos triângulos retângulos que não havíamos notado. Vejamos esse padrão: se pegarmos a diferença entre a hipotenusa e a perna dada (a menor, por exemplo), ou seja, 30 − 18 = 12, basta multiplicar o resultado da subtração por 2 e, facilmente, obtemos o valor de outra perna, ou seja, 12 · 2 = 24.

Fizemos a verificação com um triângulo mais simples, o triângulo pitagórico (3,4,5) e notamos que esse padrão se repetia: 5 − 3 = 2; 2 · 2 = 4. Porém, ao realizar o teste em outro triângulo, o (5,12,13), não foi validado, vejamos: 13 − 5 = 5; 8 · 2 = 16 ≠ 12.

Percebemos que para encontrar a solução não bastava simplesmente dobrar o resultado da subtração, pois não foi validado no triângulo (5,12,13). Então, por qual número devemos multiplicar 8 para torná-lo 12? O número que satisfaz a questão é 1,5. Assim, surgem as perguntas: para cada triângulo existe um número certo e definido para realizar tal multiplicação? Como determinar qual seria esse número?

A próxima seção apresentará o cálculo para determinar esse número que chamamos de Multiplicador de Lopes. A tabela a seguir apresenta alguns triângulos e qual seria o fator multiplicador para obter o cateto desconhecido.

Tabela 1: Valor do multiplicador

#	Cateto dado (c)	Hipotenusa (a)	a - c	Multiplicador	Cateto desconhecido (b)
1	3	5	2	2
2	6	10	4	2
3	5	13	8	1,5
4	10	26	16	1,5
5	7	25	18

Teorema de Lopes e o Multiplicador de Lopes

Tendo em vista o exposto na seção anterior, definimos o Multiplicador de Lopes e, a seguir, propomos o Teorema de Lopes.

Multiplicador de Lopes

Seja ABC um triângulo retângulo com BC = a, AC = b e AB = c e, sem perda de generalidade, temos c ≤ b < a. Dados os valores da hipotenusa e de um dos catetos, o Multiplicador de Lopes é definido como sendo 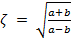 ou 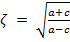 , dependendo de qual cateto foi informado. Para verificar a proposição acima, o Multiplicador de Lopes (ζ), apresentamos os cálculos utilizando os valores da tabela 1, da seção anterior, comprovando que obtivemos o valor desejado.

Tabela 2: Valor do multiplicador

#	Cateto dado (c)	Hipotenusa (a)	Multiplicador	Multiplicador de Lopes (ζ)
1	3	5	2
2	6	10	2
3	5	13	1,5
4	10	26	1,5
5	7	25

Refere-se, ainda, que o Multiplicador de Lopes também serve para o caso em que foi dada a perna maior, em vez da menor.

Teorema de Lopes

Seja ABC um triângulo retângulo com BC = a, AC = b e AB = c e, sem perda de generalidade, temos c ≤ b < a. Dados os valores da hipotenusa e de um dos catetos é possível determinar o valor do outro cateto da seguinte forma: dados os valores de a e c: b = ζ · (a − c), com 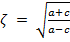; dados os valores de a e b: c = ζ · (a − b), com .

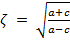Prova

Dados os valores de a e c do triângulo retângulo ABC, conforme apresentado no Teorema de Lopes, temos que .

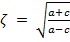Com isso: b = ζ · (a − c) ⇒ b =  .

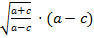Assim, elevando ao quadrado ambos os termos da igualdade, obtemos:

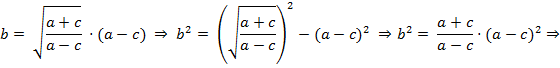
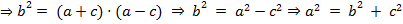
Chegamos ao resultado a² = b² + c² que é o Teorema de Pitágoras, válido para esse triângulo ABC, pois por proposição do Teorema de Lopes ele é um retângulo. A prova para b = ζ · (a − c), com 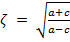 é análoga.

Considerações finais

O trabalho em sala de aula, principalmente nas séries finais do Ensino Fundamental e no Ensino Médio, deve abordar situações práticas e focar no cotidiano dos alunos, além de propor formas inovadoras de resolução dos problemas propostos aos nossos alunos.

Como pudemos ver, existem outros trabalhos que apontam para diferentes formas de abordar o tema: os triângulos retângulos e o Teorema de Pitágoras. Porém, a forma apresentada no Teorema de Lopes é diferente do que foi estudado até hoje.

Além da semelhança de triângulos e do uso do Teorema de Pitágoras, o Teorema de Lopes é uma forma alternativa de resolução de problemas. Após a verificação de alguns valores, por exemplo, em triângulos semelhantes a (3,4,5) para casos em que que falta o cateto maior, basta fazer uma subtração e uma multiplicação por 2. Assim, a prática pode tornar as aulas de Matemática mais fáceis e atraentes aos estudantes.

Referências

GIVENTAL, Alexander. The Pythagorean Theorem: What is it about? The American Mathematical Monthly, v. 113, n° 3, 2006, p. 261–65. Disponível em: https://doi.org/10.2307/27641894. Acesso em: 28 mar. 2023.

GOTEA, Mircea. O extindere a teoremei lui Pitagora. Gazeta Matematică, v. B122(4), p. 174-178, 2017.

LOPES, André Luis Martins. Otimização linear: conceito e aplicação nas aulas de Matemática para o Ensino Médio. 2017. 88f. Dissertação (Mestrado Profissional - Profmat) - Instituto de Biociências, Letras e Ciências Exatas, Universidade Estadual Paulista, São José do Rio Preto, 2017.

PAGILING, S. L. Exploration of students' representation in solving Pythagorean Theorem problems based on cognitive style. Journal of Physics: Conference Series, v. 1321, nº 3, 2019.

POLYA, G. How to solve it. A new aspect of mathematical method. 2ª ed. Princeton: Princeton University Press, 1957.

RATNER, Bruce. Pythagoras: Everyone knows his famous theorem, but not who discovered it 1000 years before him. Journal of Targeting, Measurement and Analysis for Marketing, v. 17, p. 229-242, 2009.

SAIKIA, Manjil P. The Pythagoras' Theorem. ArXiv preprint arXiv, 2013.