A sequência de Fibonacci e aplicações
Tatiara Nazaré Costa Martins
Licenciada em Matemática (UFPA - Câmpus de Abaetetuba)
Rômulo Corrêa Lima
Doutor em Engenharia de Recursos Naturais da Amazônia, professor do Profmat/CUBT/UFPA – Câmpus Abaetetuba e do curso de Licenciatura em Matemática da Facet/CUBT/UFPA
Manuel de Jesus dos Santos Costa
Doutor em Geofísica, professor do Profmat/CUBT/UFPA e do curso de Licenciatura em Matemática (Facet/CUBT/UFPA)
José Maria dos Santos Lobato Júnior
Mestre em Matemática, professor do IFPA – Câmpus Castanhal
José Francisco da Silva Costa
Doutor em Física, professor do Profmat/CUBT/UFPA e do curso de Educação no Campo (Fadecam/CUBT/UFPA)
Padrões e sequências numéricas
Uma das discussões que vêm atravessando séculos e gerando grandes debates entre os matemáticos é a seguinte: será que a Matemática é invenção humana ou ela existe por si mesma e o homem, por meio de seus raciocínios lógicos, consegue identificá-la e sistematizá-la? Essa pergunta é relevante, uma vez que, ao considerar certos ambientes, observam-se as presenças de padrões numéricos, os quais estão intimamente ligados à natureza do objeto, como se o elemento se constituísse a partir desses padrões. Para uma abordagem mais sistemática, indicam-se os trabalhos de Contador (2011), Mendes (2007), Eves (2011) e Gundlach (1992).
Um desses padrões é a sequência numérica de Fibonacci, nomeada assim em homenagem ao matemático italiano Leonardo de Pisa, mais conhecido como Fibonacci, que no século XIII estabeleceu por meio da sistematização lógico-formal a compreensão de uma sequência numérica em que cada termo é obtido somando os dois anteriores. Séculos se passaram e a sequência não foi devidamente estudada. Apenas em 1753 o matemático escocês Robert Simpson a descobriu, ao observar que a razão entre um elemento da sequência pelo seu antecessor tende a um limite numérico, conhecido como número de ouro 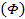 , o qual era conhecido séculos antes de Cristo pelos gregos e egípcios (Eves, 2011).
, o qual era conhecido séculos antes de Cristo pelos gregos e egípcios (Eves, 2011).
Nesse sentido, a relevância deste trabalho se estabelece quando se considera que a sequência de Fibonacci pode estar presente no cotidiano, uma vez que ela pode ser utilizada para descrever desde fenômenos naturais até a interpretação de sistemas aleatórios, como as bolsas de valores.
Aporte teórico
Por mais simples e lógicas que pareçam, em um primeiro momento, as ideias matemáticas necessitam de uma estruturação lógica, fundamentada com uso de definições e teoremas que possibilitam a sistematização do conhecimento por meio de uma formalização universal. É por isso que na Matemática qualquer conhecimento sempre estará alicerçado em bases lógicas sólidas, para que não existam incongruências de resultados. Nesse sentido, busca-se por meio deste tópico apresentar a estruturação lógica das sequências, apresentando suas definições e algumas propriedades mais importantes para assim ter uma base sólida quando for explorada a sequência de Fibonacci.
A sequência de Fibonacci
Essa sequência está associada à criação do seguinte problema, em 1202: “A partir de um casal de coelhos recém-nascidos, quantos casais de coelhos existirão após 12 meses, supondo-se que nenhum coelho morre, todo casal de coelhos tem um primeiro casal de filhotes com dois meses de idade e, após ter o primeiro casal de filhotes, gera um novo casal todo mês” (Azevedo, 2001, p. 1). Observa-se na Figura 1 a ilustração do problema.
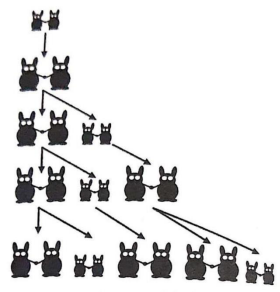
Figura 1: Crescimento da população de coelhos – Fibonacci
Fonte: Stewart, 2016.
Ao observar o enunciado do problema e a Figura 1, a quantidade de pares de coelhos a cada mês pode ser obtida considerando uma sequência recorrente, uma vez que cada termo a partir do terceiro é obtido pela soma dos dois termos anteriores.
1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233...(1)
Considerando 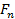 , o enésimo termo, pode-se inferir a seguinte relação entre os elementos desta sequência:
, o enésimo termo, pode-se inferir a seguinte relação entre os elementos desta sequência:
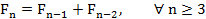 (2)
(2)
Ao analisar a sequência estabelecida, vê-se claramente que cada termo é obtido, a partir do terceiro, como a soma dos dois números anteriores a ele, ou seja, trata-se de uma sequência de recorrência de segunda ordem (Lima et al., 2004).
A sequência de Fibonacci apresenta inúmeras propriedades e relações com outros ramos da Matemática e aplicações em outras ciências (Posamentier; Lehmann, 2007; Koshy, 2017). Além disso, algumas sequências surgem a partir dos números de Fibonacci, como as sequências de Luccas (Koshy, 2017) e de Pell (Mangueira; Alves, 2020), bem como generalizações baseadas nos números de Fibonacci.
O número de ouro
A existência de números irracionais que podem ser encontrados em fórmulas das mais diversas áreas, como Geometria, Álgebra, Topologia etc., é bem conhecida. Como exemplo temos o número 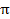 (Pi) e o número
(Pi) e o número 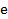 (número de Euler). No entanto, existe um número irracional que é conhecido como número de ouro ou proporção áurea, o qual representa beleza e harmonia (Mendes, 2007; Neto, 2013; Zahn, 2011). Esse número é representado pela letra grega
(número de Euler). No entanto, existe um número irracional que é conhecido como número de ouro ou proporção áurea, o qual representa beleza e harmonia (Mendes, 2007; Neto, 2013; Zahn, 2011). Esse número é representado pela letra grega 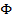 (Phi), cujo valor é:
(Phi), cujo valor é:
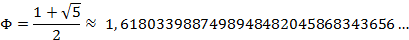 (3)
(3)
Diz-se que um ponto divide um segmento de reta em média e extrema razão ou em seção áurea se o maior dos segmentos é a média geométrica entre o menor e o segmento todo. A razão entre o maior segmento e o menor segmento chama-se razão áurea (Silva, 2015, p. 26).
A ideia geométrica da obtenção do número de ouro pode ser representada na Figura 2.
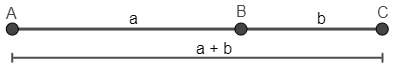
Figura 2: Segmento de reta dividido na proporção áurea
Pela definição, temos que:
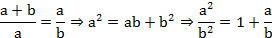
Fazendo 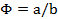 , teremos:
, teremos:
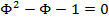
Resolvendo a equação polinomial do segundo grau, obtemos:
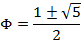
Observando que 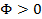 , uma vez que representa a divisão de dois comprimentos, então:
, uma vez que representa a divisão de dois comprimentos, então:
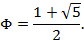
A relação entre a sequência de Fibonacci e o número de ouro: a espiral áurea
De maneira empírica, considerando a sequência de Fibonacci (1), observa-se que:
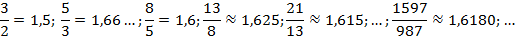
Nota-se a existência de uma relação entre a sequência de Fibonacci e o número de ouro, que é dado pelo seguinte limite:
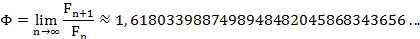
Essa relação estabelecida não foi conhecida por Fibonacci; foi o matemático escocês Robert Simpson, em 1753, que percebeu a relação e a formalizou, provando a relação por meio de da teoria de limites. Ferreira (2007) apresentou em seu trabalho um gráfico dos quocientes em função dos números que compõem a sequência, mostrando a convergência da sequência para o valor de 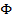 , conforme pode ser visto na Figura 3.
, conforme pode ser visto na Figura 3.
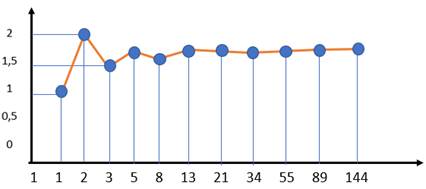
Figura 3: Quocientes entre os números de Fibonacci
Quanto maior for o número de Fibonacci dividido pelo seu antecessor, mais próximo o resultado estará do número de ouro. Também é possível, utilizando retângulos áureos juntamente com as sequências de Fibonacci, construir uma espiral, chamada espiral áurea ou logarítmica (Livio, 2008, p. 140). A Figura 4 permite visualizar essa construção.
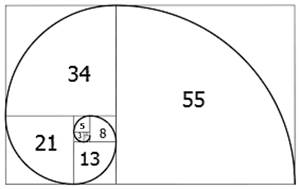
Figura 4: Construção da espiral áurea a partir da utilização da sequência de Fibonacci como lados de quadrados
Fonte: Reis, 2019.
De posse desses aportes teóricos, será possível analisar, utilizando fundamentação lógico-matemática alguns elementos na arte, na natureza e na bolsa de valores que possibilitam a visualização dos padrões da sequência de Fibonacci e do número de ouro.
Onde se encontra a sequência de Fibonacci?
Os padrões gerados a partir da sequência de Fibonacci, do número de ouro e da espiral áurea aparecem nas mais variadas áreas do nosso cotidiano. A seguir serão apresentadas algumas de suas aplicações.
Na natureza
A natureza é um ambiente em que facilmente se encontram padrões numéricos, desde os fenômenos periódicos, atmosféricos, na fauna e na flora (Mendes, 2007). Para citar alguns exemplos da sequência de Fibonacci e do número de ouro na natureza, serão tomados elementos da fauna, da flora e do universo observável.
Fauna
No trabalho de Freitas (2008), destaca-se o antílope (Antilopecervicapra), o camaleão (Chamaeleonidae) e o nautilus marinho (Nautilus pompilius) como animais que apresentam a sequência de Fibonacci e o número de ouro por meio da espiral áurea, conforme pode ser visualizado na Figura 5.

Figura 5: Exemplos da formação da espiral áurea no antílope, no camaleão e no nautilus
Fonte: Freitas, 2008.
Apesar dos diferentes habitats, a presença do número de ouro e da sequência de Fibonacci em suas estruturas são aparentes.
Flora
Alguns seres do reino vegetal também apresentam a espiral áurea, pois, segundo Zahn (2011) e Passi e Rodrigues (2013), esse padrão pode ser observado no arranjo de folhas, ramos e troncos de plantas, pétalas de flores e sementes. Nos arranjos de folhas, temos as bromélias e as aloés espiral, que “obedecem à regra de formação da espiral áurea. De acordo com muitos biólogos, esse arranjo é relevante na captação uniforme de raios solares e no escoamento das águas das chuvas” (Zahn, 2011, p. 41). A forma geométrica apresentada pela bromélia e pela aloés é perfeitamente apropriada para a captação de água, como se a disposição das folhas funcionasse como condutores de água das extremidades até ao centro, conforme mostrado na Figura 6.

Figura 6: Padrão de espiral áurea nas folhas da bromélia e da aloés
Fonte: Passi; Rodrigues, 2013.
Em se tratando de ramos e troncos de plantas, a Achilleaptarmica é uma perfeita representante em evidenciar a sequência de Fibonacci, pois, ao se observar a estrutura do caule e galhos, pode-se constatar que o crescimento acompanha uma sequência lógica que contempla os quatro primeiros números de Fibonacci, como pode ser visto na Figura 7.

Figura 7: Os números de Fibonacci aparecem na formação do caule da Achilleaptarmica
Fonte: Neto, 2013.
No caso das flores, muitas apresentam a quantidade de suas pétalas e a distribuição delas fazendo uso da sequência de Fibonacci; é o caso do lírio, que tem três pétalas; a prímula tem cinco pétalas; o delfínio, oito pétalas; a erva-de-são-tiago, treze pétalas; e a chicória, 21 pétalas, como mostrado na Figura 8.

Figura 8: As quantidades de pétalas do lírio, da prímula, do delfínio, da erva-de-são-tiago e da chicória, nessa ordem, formam parte da sequência de Fibonacci
Fonte: Livio, 2008.
Deve-se observar que a flor margarida pode ter 13, 21 ou 34 pétalas; os girassóis, dependendo do seu tamanho, podem ter 21, 34, 55, 89 ou 144 pétalas, organizadas em espiras, na primeira fileira. Na segunda fileira podem ter 34, 55, 89, 144 ou 233, organizadas em espiras. Na terceira, 55, 89, 144, 233 ou 377 e assim sucessivamente; todos esses números são parte da sequência de Fibonacci (Mendes, 2007) mostrada na Figura 9.

Figura 9: 55 espiras à esquerda e 34 à direita
Fonte: Mendes, 2007.
Galáxias e furacões
O atual sistema de classificação de galáxias foi modificado e corrigido várias vezes, mas os astrônomos ainda reconhecem os cinco principais tipos de galáxias. São elas: espirais, espirais barradas, elípticas, lenticulares e irregulares. Na Figura 10, destaca-se a galáxia espiral e sua forma que obedece à espiral áurea. Nesse caso particular, as galáxias espirais têm núcleo inchado de estrelas mais velhas da população, das quais saem “braços” espirais destacados por regiões de formação de estrelas e aglomerados brilhantes de estrelas luminosas de vida curta (Sparrow, 2018).

Figura 10: Comparação entre as formas de uma galáxia e a espiral áurea
Fonte: Sparrow, 2018.
Um furacão é um tipo de ciclone tropical que tem origem em águas oceânicas, caracterizando grandes áreas de nuvens carregadas que só podem ser observadas nas imagens de satélites, podendo causar graves consequências quando atinge áreas urbanas (Rocha et al., 2015). Sua forma também está relacionada à espiral áurea.
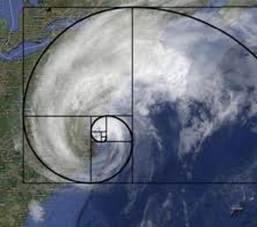
Figura 11: Confrontação entre os formatos de um furacão e da espiral áurea
Fonte: Arruda, 2013.
Nas artes
As criações artísticas e publicitárias chamam muita atenção das pessoas que as apreciam. Isso acontece por várias razões, seja pelas cores, pelos desenhos ou pelos designs. Muitas dessas criações utilizam em suas elaborações a sequência de Fibonacci e o número de ouro, permitindo que as criações apresentem “algo diferenciado” (Zahn, 2011). Nas artes, especialmente na Renascença, muitas obras apresentam a espiral áurea em suas elaborações; a mais famosa é o quadro A Monalisa, de Leonardo da Vinci, no qual as relações são entre seu tronco e cabeça e entre elementos do rosto (Freitas, 2008).

Figura 12: A Monalisa e a espiral áurea
Fonte: Freitas, 2008.
Como já mencionado, a utilização do número de ouro e da sequência de Fibonacci tem uma única intenção: obter harmonia, beleza e perfeição. Outros dois exemplos, apesar de épocas distintas, também fizeram uso do número de ouro. Na arquitetura, há o templo de Parthenon e, em outro exemplo nas artes, está a obra de Sandro Botticelli, O nascimento de Vênus (Freitas, 2008).

Figura 13: O Parthenon e O nascimento de Vênus em contraposição com as espirais áureas
Fonte: Freitas, 2008.
Bolsa de valores
De tudo que foi apresentado até agora, pode-se fazer o seguinte questionamento: será que a sequência de Fibonacci e o número de ouro estão presentes somente em naturezas lineares, ou seja, que não apresentam indeterminações e aleatoriedade?
Em um primeiro momento, a resposta seria sim, uma vez que a relação entre a sequência e o número de ouro apresenta harmonia visual e estética. No entanto, no contexto caótico das bolsas de valores, devido às oscilações de subida e queda do valor das ações, Elliott observou a presença da sequência de Fibonacci. A movimentação de mercado não acontece de forma linear. Há crescimento, seguido de correção, não necessariamente nessa ordem. Esse fenômeno de crescimento ou decrescimento (progressão) de mercado se dá em forma de ondas (Elliott, 1994; Belini, 2015, p. 66).
A Teoria das Ondas de Elliott afirma que, nos mercados, progressões têm estrutura específica de cinco ondas. Três dessas ondas, classificadas como 1, 3, 5, efetuam movimento direcional a favor da tendência e são separadas por duas interrupções contra a tendência, que são classificadas como ondas 2 e 4 (Belmont, 2010, p. 34).
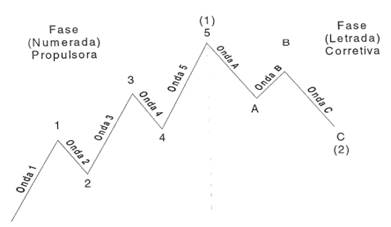
Figura 14: Ciclo das ondas de Elliott
Fonte: Frost; Prechter, 2002.
Outra forma de expandir a compreensão sobre as propriedades da sequência de Fibonacci se dá por meio da razão inversa entre os elementos da sequência, que também gera uma constante 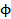 . Os matemáticos designaram esses valores como phi (0,618) e Phi (1,618) (Frost; Prechter, 2002).
. Os matemáticos designaram esses valores como phi (0,618) e Phi (1,618) (Frost; Prechter, 2002).
Utilizando esta relação,
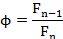
na sequência (1), observa-se que:
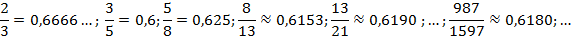
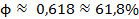
Deve-se observar que, ao dividir esses números, alternando a sequência, pulando um elemento da sequência, por exemplo, 55/144, se obtém um segundo nível percentual de aproximadamente de 38,2% que, ao somar ao percentual do número de ouro, obtém-se 100% (Frost; Prechter (2002).
O que Elliott observou foi que os números de Fibonacci podem ser utilizados na análise técnica, especialmente na Teoria das Ondas, que permite a determinação das porcentagens de correção para cada tendência, de crescimento ou decrescimento, ou seja, de subida ou queda em cada investimento, evidenciando que se trata de previsão de caráter matemático, dentro de um contexto com parâmetros; não é uma previsão do futuro. Os parâmetros mais importantes são, segundo Ribeiro (2014, p. 136), as percentagens de 61,8% e 38,2% para estabelecer o nível máximo e o nível mínimo, respectivamente, na correção de um movimento, conforme mostra a Figura 15.
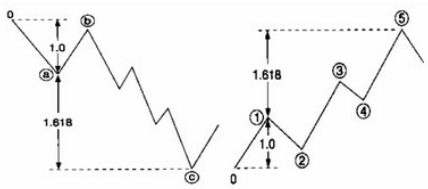
Figura 15: Obtenção do número de ouro nas ondas de Elliot
Fonte: Belini, 2015.
Com essas fermentas à disposição, o trader (investidor do mercado financeiro que busca ganhar dinheiro com operações de curto prazo, aproveitando-se da volatilidade do mercado) deve ficar atento, uma vez que os percentuais 38,2% e 61,8% são indicativos de que os preços das ações tendem a passar por um período de correção. Em termos práticos, os números de Fibonacci identificam zonas de alerta, indicando possíveis resistências, suportes ou reversões. A Figura 16 apresenta a variação de um investimento em determinada ação da bolsa de valores.
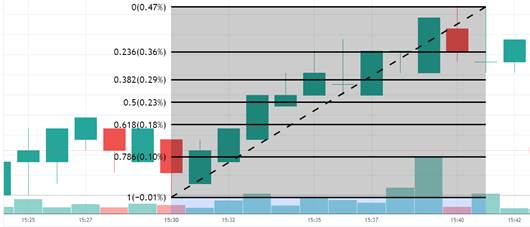
Figura 16: Análise de um investimento real utilizando a série numérica de Fibonacci
Assim, de maneira geral, pode-se afirmar que os percentuais de Fibonacci marcam os pontos antes de uma reversão, permitindo que o trader consiga efetuar suas operações orientado por essas leituras de gráficos do movimento de bolsa de valores (Ribeiro, 2014); essas situações podem ser observadas na Figura 17.
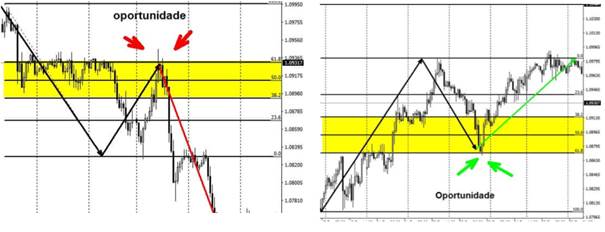
Figura 17: Expansão e retração de Fibonacci
Fonte: Banco Modal, 2022.
Considerações finais
A sequência de Fibonacci não é um conhecimento do passado; é atual e está sendo utilizado em várias construções arquitetônicas e design de slogan das grandes marcas mundiais, pois apresenta a capacidade de harmonizar o campo visual, tornando a imagem ou objeto agradáveis de observar. Outro ponto a ser destacado é a espiral áurea, que é a combinação da sequência de Fibonacci e do número de ouro, por meio da criação de quadrados e retângulos. Essa organização sequencial por meio dos números da sequência possibilita a criação dessa curva, que, como visto, está presente na natureza das mais variadas formas, apresentando beleza, estética e harmonia.
Por outro lado, observou-se a possibilidade de aplicação da sequência de Fibonacci em sistemas aleatórios, como nas bolsas de valores, em que, apesar das oscilações constantes entre crescimento e queda, é possível usar parâmetros para estimar até que ponto podem ocorrer essas expansões e retrações usando o número de ouro. Aplicações como essas mostram a dinamicidade das sequências de Fibonacci e permitem que áreas complexas sejam estudadas e estimadas por meio da sequência.
A proposta apresentada é parte de um todo que ainda está em desenvolvimento e precisa ser ampliado, já que existem outros desdobramentos de aplicações da sequência de Fibonacci que podem ser tomados como desenvolvimento de pesquisa.
Referências
AZEVEDO, A. Sequências de Fibonacci. Revista do Professor de Matemática, Brasília, nº 45, 2001.
BANCO MODAL. Modalmais. s/d. Disponível em: https://www.modalmais.com.br/blog/o-que-e-trader. Acesso em: 29 jan. 2022.
BELINI, M. M. A razão áurea e a sequência de Fibonacci. 2015. 86f. Dissertação (Mestrado em Matemática em Rede Nacional) – Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, São Carlos, 2015.
BELMONT, D. F. S. Teoria das Ondas de Elliott: uma aplicação ao mercado de ações da BM&FBovespa. Dissertação (Mestrado) – Universidade Federal da Paraíba, 2010. Disponível em: https://repositorio.ufpb.br/jspui/handle/tede/5048?locale=pt_BR#:~:text=Resumo%3A,produtos%20geram%20processos%20de%20volatilidade. Acesso em 12 jan. 2022.
CONTADOR, P. R. M. A Matemática na arte e na vida. 2ª ed. São Paulo: Livraria da Física, 2011.
ELLIOTT, R. N. Como funciona o Princípio da Onda e sua correlação com as leis matemáticas. Nova York: New Classics, 1994.
EVES, H. Introdução à história da Matemática. Trad. Hygino H. Domingues. 5ª ed. Campinas: Editora da Unicamp, 2011.
FERREIRA, R. A. Sequência de Fibonacci. [S.l.], 2007.
FREITAS, F. M. de. A proporção áurea e curiosidades históricas ligadas ao desenvolvimento da ciência. Florianópolis: UFSC, 2008. Disponível em: http://www.africamae.com.br/wp-ontent/pdf/aurea.pdf. Acesso em: 10 jan. 2022.
FROST, A. J. E.; PRECHTER, R. R. O Princípio da Onda de Elliott. Rio de Janeiro: Editec, 2002.
GUNDLACH, B. H. História dos números e numerais. Trad. Hygino H. Domingues. São Paulo: Atual, 1992.
KOSHY, T. Fibonacci and Lucas numbers with applications. v. 1. 2ª ed. Hoboken: John Wiley & Sons, 2017. (Series: Pure and applied mathematics.)
LIMA, E. L. et al. A Matemática do Ensino Médio. v. 2. 5ª ed. Rio de Janeiro: IMPA, 2004. (Coleção do Professor de Matemática.)
LIVIO, M. Razão áurea: a história de Fi, um número surpreendente. 3ª ed. Rio de Janeiro: Record, 2008.
MANGUEIRA, M. C. S.; ALVES, F. R. V. Números híbridos de Fibonacci e Pell. Revista Thema, v. 17, nº 3, p. 831-842, 2020. DOI: http://dx.doi.org/10.15536/thema.
MENDES, F. M. P. A Matemática na natureza. Dissertação (Mestrado) - Universidade de Trás-os-Montes e Alto Douro, Vila Real, 2007. Disponível em: http://repositorio.utad.pt/bitstream/10348/74/1/msc_fmpmendes.pdf. Acesso em: 10 jan. 2022.
NETO, P. R. de S. A aplicação do número de ouro como recurso metodológico no processo de ensino-aprendizagem. Dissertação (Mestrado) — Universidade Federal do Piauí, Teresina, 2013. Disponível em: http://bit.profmatsbm.org.br/xmlui/bitstream/handle/123456789/515/2011_00411_PABLO_ROBERTO_DE_SOUSA_NETO.pdf?sequence=1. Acesso em: 11 jan. 2022.
PASSI, D. C.; RODRIGUES, C. T. V. Sequência de Fibonacci. Campinas: Unicamp, 2013. Disponível em: http://www.ime.unicamp.br/~ftorres/ENSINO/MONOGRAFIAS/DC_M1_FM_2013.pdf. Acesso em: 05 jan. 2022.
POSAMENTIER, A. S.; LEHMANN, I. The fabulous Fibonacci numbers. Buffalo: Prometheus Books, 2007.
RIBEIRO, Sandra Cristina Antunes. Aplicação do Princípio das Ondas de Elliott à bolsa portuguesa. Tese (Doutorado) – Universidade Aberta de Lisboa, Lisboa, 2014. Disponível em: http://hdl.handle.net/11144/431. Acesso em: 16 jan. 2022.
ROCHA, Fabio Pinto da; ARAVÉQUIA, José Antonio; RIBEIRO, Bruno Zanetti. Estudo de ciclones e de padrões de circulação atmosférica no Oceano Atlântico Sul próximo à costa das Regiões Sul e Sudeste do Brasil usando dados da reanálise do era-interim. Revista Brasileira de Meteorologia, v. 31, nº 2, p. 141-156, 2016. Disponível em: https://www.scielo.br/j/rbmet/a/58xkj9mWhJmJX58b7D7PV6x/?format=pdf&lang=pt. Acesso em: 12 jan. 2022.
SILVA, R. L. A sequência de Fibonacci e o número de ouro: contexto histórico, propriedades, aplicações e propostas de atividades didáticas para alunos do 1º ano do Ensino Médio. Dissertação (Mestrado em Matemática) – Universidade Estadual do Sudoeste da Bahia, Vitória da Conquista, 2015. Disponível em: http://www2.uesb.br/ppg/profmat/wp-content/uploads/2018/11/Dissertacao_REGINALDO_LEONCIO_SILVA.pdf. Acesso em: 11 jan. 2022.
SPARROW, G. 50 ideias de Astronomia que você precisa conhecer. São Paulo: Planeta, 2018.
STEWART, Ian. O fantástico mundo dos números: a Matemática do zero ao infinito. Rio de Janeiro: Zahar, 2016.
ZAHN, M. Sequência de Fibonacci e o número de ouro. Rio de Janeiro: Ciência Moderna, 2011.
Publicado em 10 de setembro de 2024
Como citar este artigo (ABNT)
MARTINS, Tatiara Nazaré Costa; LIMA, Rômulo Corrêa; COSTA, Manuel de Jesus dos Santos; LOBATO JÚNIOR, José Maria dos Santos; COSTA, José Francisco da Silva. A sequência de Fibonacci e aplicações. Revista Educação Pública, Rio de Janeiro, v. 24, nº 33, 10 de setembro de 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/33/a-sequencia-de-fibonacci-e-aplicacoes
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

