Resolução de problemas nos processos de ensino de Matemática na Educação Básica: uma proposta com alunos do 6º ano do Ensino Fundamental
André Silveira do Amaral
Mestre em Ensino, Educação Básica e Formação de Professores (UFES), docente da EMEIEF Ercy Arruda Bonfim
Jorge Henrique Gualandi
Doutor em Educação Matemática (PUC-SP), docente do IFES
Vanessa Holanda Righetti de Abreu
Doutora em Biologia Vegetal (UERJ), docente da UFES
No ensino da disciplina de Matemática na Educação Básica da rede municipal de Muqui, no sul do Estado do Espírito Santo, constatam-se repetitivas dificuldades de alunos em atividades que envolvem a resolução de problemas matemáticos. Nesse sentido, os alunos devem se reinventar diante das adversidades, estando abertos às mudanças. Isso permite que se tornem protagonistas na construção do conhecimento.
No trabalho em sala de aula, os problemas matemáticos tanto práticos como teóricos, permeiam o ensino da Matemática. Isso permite gerar, desenvolver e exercitar habilidades, como o raciocínio lógico, o senso crítico e a interpretação. Segundo a Base Nacional Comum Curricular (Brasil, 2018), a Matemática desempenha uma função fundamental no processo de sistematização do pensamento e na execução de problemas que envolvem situações do cotidiano do estudante.
Em relação ao ensino da Matemática para o 6º ano do Ensino Fundamental, a BNCC apresenta 34 habilidades especificadas por códigos alfanuméricos, das quais se destacam para o estudo, a habilidade EF06MA03: “resolver e elaborar problemas que envolvam cálculos com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora” (Brasil, 2018, p. 301). Essa habilidade é pertinente ao objeto de conhecimento das “operações com números naturais”, dentro do campo temático “números”.
Diante disso, há a pergunta: “Em função da dificuldade de entendimento matemático, como os estudantes do 6º ano mobilizam seus conhecimentos mediante a resolução de vários tipos de problemas de Matemática?”.
Por isso, o foco se assentou nas contribuições metodológicas de resolução de problemas, na construção do pensamento matemático; a pesquisa tem por objetivo investigar como a metodologia de ensino e aprendizagem de resolução de problemas, proposta por Pólya (2006), auxilia os alunos do 6º ano na mobilização de conhecimentos matemáticos para a resolução de diferentes tipos de problemas matemáticos definidos por Dante.
O estudo visa investigar como a metodologia de ensino e aprendizagem de resolução de problemas, proposto por Pólya (2006), auxilia os alunos do 6º ano na mobilização de conhecimentos matemáticos para a resolução de diferentes tipos de problemas matemáticos definidos por Dante.
Algumas concepções sobre “problemas”, “exercícios” e o método heurístico de Pólya
Desde os primórdios, a humanidade enfrenta problemas que necessitam de solução, seja para a sua subsistência, seja para o convívio em comunidades (D’Ambrósio, 2013). Portanto, ao se referir ao termo “problema”, recorda-se de significados distintos, desde a variação do contexto no qual as pessoas estão inseridas até suas qualidades.
Para Souto e Guérios (2017), Pólya foi um dos primeiros estudiosos a dar proeminência na resolução de problemas, caracterizando-a como uma coisa original, que conduz o estudante a criar novos planos de solução que estimulem sua curiosidade e despertam o seu interesse.
Para uma melhor compreensão dessas concepções é importante definir o que é “problema” e o que é “exercício”. A partir disso, Mateus et al. (2001, p. 4) explicam:
O exercício é uma atividade de adestramento no uso de alguma habilidade ou conhecimento matemático já conhecido pelos resolvedores, como a aplicação de algum algoritmo ou fórmula já conhecida. Ou seja, o exercício envolve mera aplicação de resultados teóricos enquanto o problema necessariamente envolve invenção e/ou criação significativa (grifo nosso).
Os problemas e os exercícios estão presentes nas aulas de Matemática. Para Pozo (1998, p. 16), “o problema se diferencia de um exercício, na medida em que, neste último caso, dispõem-se de mecanismos que levam, de forma imediata, à solução”. A partir dessa abordagem, Martins (2019) alega que só existe um problema quando há um objetivo a ser atingido e é preciso pensar em estratégias para resolvê-lo.
Na percepção de Dante (1991, p. 10), problema “é qualquer situação que exija o pensar do indivíduo para solucioná-la”. Nesse contexto, o autor traz uma abordagem interessante entre a diferença de “exercício” e “problema”, no ensino da Matemática.
Logo, exercício é um ato que conduz o aluno a treinar e executar a aplicação das operações matemáticas já inseridas nas questões. O problema, também chamado de “situação-problema”, exige do educando uma estratégia para a resolução, pois as operações matemáticas não estão coesas no enunciado. Não pode ser resolvido pela aplicação automática de fórmulas, pois requer um andamento mais longo para pensar sob um plano de ação (Dante,1995).
Além da definição de “problema”, há a definição de “exercícios” que são aplicações de algoritmos que auxiliam o aluno a reconhecer e reforçar os conhecimentos adquiridos anteriormente. Tanto “problema” quanto “exercícios” são classificados de diferentes maneiras em função do objetivo que se pretende alcançar no processo de ensino-aprendizagem dos conceitos matemáticos (Dante, 2010).
De forma resumida, Souto e Guérios (2017, p. 6) explicam que o problema matemático é:
uma situação nova e desafiadora, a qual não se pode resolver mecanicamente [...] requer, então, a construção de caminhos na busca de uma solução, podendo, na maioria dos casos, admitir mais de uma possibilidade de resolução. Já os exercícios matemáticos são situações em que o estudante se depara e já sabe resolver.
Posteriormente, Dante (2010) sugeriu novas definições de problemas e exercícios, diferenciando-os em sete tipos: exercícios de reconhecimento, exercícios de algoritmos, problemas-padrão simples, problemas-padrão compostos, problemas-sucesso ou heurístico, problemas de aplicação e problemas de quebra-cabeça.
Exercícios de reconhecimento são aqueles nos quais o aluno reconhece uma propriedade, enquanto os exercícios de algoritmos podem ser resolvidos passo a passo. Já os problemas-padrão podem ser resolvidos com uma única operação, enquanto problemas padrão-composto são resolvidos com duas ou mais operações. Os problemas-sucesso ou heurísticos envolvem operações que não estão explícitas no enunciado. Problemas de aplicação ou situações-problema contextualizadas são os problemas que retratam situações reais do dia a dia. Por fim, os problemas de quebra-cabeça ou de Matemática recreativa que são problemas que desafiam os alunos.
Na Matemática, solucionar problemas é algo habitual em todo e qualquer lugar, principalmente em vários ramos da Ciência (formais, naturais, sociais). É perceptível que há vários conceitos para a resolução de problemas dentro do contexto da Matemática escolar, porém, para Branca (1997, p. 4), a “resolução de problemas”
é uma expressão abrangente que pode significar diferentes coisas para diferentes pessoas ao mesmo tempo e diferentes coisas para as mesmas pessoas em diferentes ocasiões. As três interpretações mais comuns de resolução de problemas são: (1) como uma meta, (2) como um processo e (3) como uma habilidade básica.
No Brasil, atualmente, é possível observar a importância das habilidades relacionadas à resolução de problemas por meio da alta quantidade de referências ao tema na BNCC, destacando-se para o 6°ano a habilidade EF06MA03 (Brasil, 2018).
A partir das orientações educacionais dispostas na BNCC, a resolução de problemas possibilita aos estudantes mobilizarem conhecimentos, desenvolver as habilidades básicas e a capacidade de gerenciar as informações que estão na sua consecução. O fato de ser estimulado a compreender, elaborar, executar e verificar o problema, evidencia uma concepção de ensino-aprendizagem não pela mera reprodução de conhecimentos. Nesse sentido, o estudo da resolução de problemas com base nos princípios de Pólya (2006) é justificado pelo fato de que o autor enfatiza a resolução de problemas como uma habilidade.
Método heurístico de George Pólya
George Pólya nasceu em 1887 em Budapeste e depois de graduado fez doutorado em Probabilidade, em 1912. Trabalhou por 26 anos no Instituto Federal de Tecnologia de Zurique, Suíça. Foi nesse período que Pólya teve contato com renomados matemáticos que desenvolveram várias pesquisas na área da Matemática. Na década de 1940, mudou-se para a Califórnia, nos Estados Unidos. Em 1945, publicou sua primeira obra, How to solve it, na qual compartilha seus pensamentos a respeito da resolução de problemas e os métodos heurísticos. Foi em 1953 que ele recebeu o título de professor emérito (Guimarães, 2010).
Ao abordar a Heurística, é preciso antes conceituar a palavra. Para Pólya (2006, p. 99), a Heurística
era o nome de um certo ramo de estudo, não bem delimitado, pertencente à Lógica, à Filosofia ou à Psicologia, muitas vezes delineado, mas raramente apresentado com detalhes, hoje praticamente esquecido. O objetivo da Heurística é o estudo dos métodos e das regras da descoberta e da invenção.
Assim sendo, a Heurística é a ciência que discute o estudo das constantes atividades da concepção do criador. A Heurística moderna tem como finalidade compreender o método solucionador dos problemas, sobretudo as operações intelectuais típicas do processo de ensino-aprendizagem, as quais não podem ser desprezadas. A pesquisa de Pólya afirma que um “estudo consciencioso da Heurística deve levar em conta, tanto as bases lógicas quanto as psicológicas” (Pólya, 2006, p. 99). Isso posto, uma compreensão das operações cognitivas adequadas à resolução de problemas exerce uma influência propícia do ensino da Matemática, pois ao mesmo tempo “avalia a importância da resolução dos problemas na evolução da matemática, descoberta de novos resultados, criação de novos problemas, também ressalta a importância dos problemas no processo ensino-aprendizagem” (Mateus et al., 2001, p. 8).
Embasado na sua experiência como educador de Matemática, Pólya escreveu, em How to solve it (1945), as quatro fases de Pólya, de forma clara e objetiva: fase 1 - compreender o problema; fase 2 - elaborar um plano; fase 3 - executar o plano; e a fase 4 - verificação de todo processo.
A primeira fase é compreender o problema. Nela, é importante que o estudante se familiarize com a situação e identifique o valor a ser determinado, assim como os dados envolvidos. Selecionar os dados, nessa etapa, contribui para organizar a sequência da tarefa (Pólya, 2006). Para compreender um problema em Matemática é necessário “estabelecer uma relação afetiva entre a língua materna e o contexto interdisciplinar da Matemática” (Soares; Oliveira, 2016, p. 3).
Após a familiarização com o problema, inicia-se a segunda fase da resolução de problemas, de elaboração do plano, vinculada diretamente à primeira. Nessa fase, o aluno escolhe o que precisa ser feito para solucionar a situação-problema, sendo aconselhável buscar problemas análogos. Assim, é necessário retornar aos conhecimentos matemáticos anteriormente adquiridos para que ocorra o aprimoramento da compreensão do problema (Pólya, 2006).
Na fase de aprimoramento da compreensão é possível trazer algumas argumentações antes de executar o plano, como: você já solucionou um problema semelhante a este? Possui em mente algum problema equivalente a esse que possa lhe ajudar na solução? Existe possibilidade de ser resolvido o problema por partes? As respostas a essas indagações são essenciais para orientar a preparação da estratégia de solucionar o problema (Pólya, 2006).
A terceira fase trata da execução do plano. O primeiro questionamento a ser feito é “Por onde começar?”. Nessa etapa, cada passo do plano deve ser verificado, exigindo persistência. Toda essa ação depende da formulação de um excelente plano ao redor da situação apresentada, ou seja, quanto mais minucioso for o plano, mais fácil será a sua execução, chegando, assim, a um resultado satisfatório (Pólya, 2006).
Portanto, é nessa fase que o estudante usa os conceitos e procedimentos matemáticos adquiridos durante toda a vida escolar para solucionar o problema. Como afirma Brito (2006, p. 19), “a solução de problemas é, portanto, geradora de um processo através do qual o aprendiz vai combinar, os conceitos, princípios, procedimentos, técnicas, habilidades e conhecimentos adquiridos para encontrar a solução”. Então, segue-se para a última fase que corresponde ao processo de verificar se o plano foi bem executado, avaliar a necessidade de ajustes e a coerência da resposta.
Segundo Gazzoni e Ost (2008, p. 44), utilizando o método proposto por Pólya, constata-se que os estudantes aprendem
com mais facilidade, organizam-se as ideias e se obtém a solução do problema com melhor compreensão do que se não tivéssemos seguido seu método. Também é possível encontrar problemas análogos e tornar mais clara uma estratégia para sua resolução. Certamente esse método não é uma ferramenta milagrosa, mas torna-se necessário e eficiente seu uso em um grande número de problemas, principalmente os que apresentam um maior nível de dificuldade.
Portanto, é importante destacar que todos os métodos utilizados são sugestões para guiar o aluno na construção de novos conhecimentos e habilidades.
Procedimentos metodológicos
No referido estudo de abordagem qualitativa, os sujeitos da pesquisa foram os estudantes do 6º ano do Ensino Fundamental de uma escola municipal de Muqui, cidade no Estado do Espírito Santo. A pesquisa de campo foi desenvolvida no período de setembro a outubro de 2022, com prévia assinatura do Termo de Anuência (Secretaria Municipal de Educação), do Termo de Consentimento Livre e Esclarecido e do Termo de Assentimento (os responsáveis pelos alunos autorizaram a participação dos alunos, pois estes são menores de idade).
A presente pesquisa se insere nas discussões de resolução de problemas, enquanto uma proposta metodológica para o ensino da Matemática escolar. O aporte teórico balizador parte principalmente dos pressupostos de Pólya (2006) e Dante (2010). Na produção de dados, utilizaram-se as quatro fases de Pólya (2006).
A pesquisa teve alguns registros do trabalho de campo coletados por meio de observações e da lista de situações-problema. Aplicou-se uma lista de situações-problema envolvendo vários tipos de problemas, propostos por Dante (2010), com o intuito de investigar as estratégias usadas pelos sujeitos da pesquisa. Em seguida, foi feita socialização, apresentando a eles as quatro fases de Pólya (2006), sem mencioná-las.
A coleta/produção de dados ocorreu por meio de dois encontros na escola municipal, lócus da investigação, no turno vespertino, a partir das 13 horas. Cada encontro teve duração de 2 horas. Na turma do 6° ano I, os encontros foram realizados das 13h às 15h. Os encontros com o 6° ano II foram realizados após o recreio, das 15h20 às 17h20. Vale ressaltar que a produção de dados ocorreu após a aprovação pelo Comitê de Ética de Pesquisa com Seres Humanos (CEP) da Universidade Federal do Espírito Santo, câmpus Alegre, sob a aprovação nº 5.549.301. Os dados foram analisados e interpretados conforme a revisão bibliográfica que aborda a resolução de problemas no ensino da Matemática escolar e socialização das resoluções utilizadas.
Apresentação dos resultados
Os sujeitos da pesquisa foram organizados em duplas e trio. No 6° ano I, foram formadas seis duplas e, no 6° ano II, cinco duplas e um trio (Quadro 1).
Quadro 1: Distribuição das duplas e trio dos sujeitos de pesquisa do 6º ano I e 6º ano II
Dupla A |
Antônio e Artur |
Dupla B |
Betânia e Beto |
Dupla C |
Carlos e Claudia |
Dupla D |
Daniela e Daiana |
Dupla E |
Eva e Eloá |
Dupla F |
Fábio e Fernando |
Dupla G |
Geraldo e Guto |
Dupla H |
Henrique e Hélio |
Dupla I |
Igor e Iago |
Dupla J |
Joaquim e Jorge |
Dupla K |
Kellen e Kátia |
Trio L |
Lucas, Luan e Leonara |
No primeiro encontro (em 22 de setembro de 2022), as duplas e o trio receberam uma lista contendo seis situações-problema para solucionarem a questão, no ínterim de 2h, de acordo com seus entendimentos, sem a interferência do pesquisador.

Figura 1: Resolução dos problemas realizada pelos sujeitos da pesquisa
No segundo encontro (6 de outubro de 2022), foi proposta a socialização com os sujeitos da pesquisa a fim de que apresentassem as estratégias utilizadas para resolver os problemas da primeira lista no quadro branco. Observou-se que os sujeitos da pesquisa, ao apresentarem suas estratégias de resolução, expuseram uma melhora na compreensão dos conceitos matemáticos.
Depois da socialização das estratégias de resoluções, o pesquisador realizou uma intervenção resolvendo as situações-problema, utilizando as quatro fases da resolução de problemas propostos por Pólya (2006), porém não as mencionou.
No Gráfico 1, apresentamos o quantitativo de acertos e erros das duplas e do trio, situações-problema que foram resolvidas pelos sujeitos da pesquisa em diferentes tipos selecionados a partir da classificação de Dante (2010).
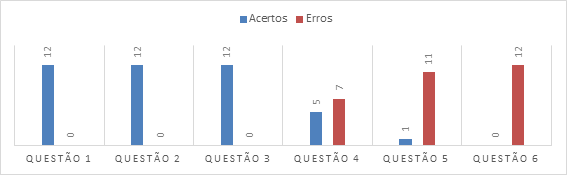
Gráfico 1: Levantamento de acertos e erros referente à primeira lista de situações-problema
A questão 1 traz exercícios de reconhecimento; a questão 2, exercícios de algoritmos; a questão 3, problemas-padrão simples; a 4, problemas-padrão composto; a questão 5, problemas-processo ou heurísticos e a questão 6, problemas de quebra-cabeça.
A questão 1 é um tipo de problema: exercício de reconhecimento que Dante (2010, p. 24) atribui à finalidade de fazer com que o estudante “reconheça, identifique ou lembre de um conceito, um fato específico, uma definição etc.” As soluções das duplas A, B, C, D, E, F, G, H, I, J e do trio L para a questão 1 se deu por meio do uso da mesma estratégia, com destaque para as evidências descritas pela dupla K.

Figura 2: Resolução da dupla K da questão 1 da primeira lista de situações-problema
Fonte: Dante (2010, p. 24).
No transcorrer da pesquisa, nota-se que a dupla K dialogou entre si a respeito da definição de números pares e ímpares, conforme apresentado:
Kellen: Par é número que divide por 2, certo? Já o ímpar ele não dá para dividir por 2.
Kátia: Sim, mas para ser par basta a gente olhar o número se termina em 0, 2, 4..., aí ele é par. É isso, né? E se terminar em 1, 3, 5, 7 e 9 é ímpar.
Kellen: Ah! A professora já falou isso para gente, lembra?
Kátia: Então vamos acertar a questão (Trecho do 1º encontro, em 22 set. 2022).
Observa-se que as discussões estão em coerência com a Base Nacional Comum Curricular (BNCC), na qual esses termos devem ser trabalhados desde o 1º ano dos Anos Iniciais do Ensino Fundamental na “Unidade Temática: Números, Objetos de Conhecimentos: Leitura, escrita e comparação de números naturais e Reta numérica e Habilidade (EF01MA05) para comparar números naturais de até duas ordens em situações cotidianas” (Brasil, 2018, p. 277-278).
O reconhecimento das palavras que são lidas e os objetos matemáticos propostos por tais palavras facilitam a compreensão do problema (Vallilo, 2016). Entende-se que o enunciado dessa questão facilitou a compreensão do processo. Complementando a ideia, Goulart e Aguiar (2019) afirmam que é preciso trabalhar o conceito de palavras no ambiente escolar, a fim de potencializar a interação e a mediação para a construção de saberes e definições.
Já na questão 2 foram obtidos 12 acertos e nenhum erro. Trata-se de um tipo de problema: exercício de algoritmos, que se constituem em exercícios que usam algoritmos envolvendo as quatro operações básicas da Matemática Escolar, possibilitando treinar o desenvolvimento de algoritmos e reforçar aprendizados anteriores (Dante, 2010).
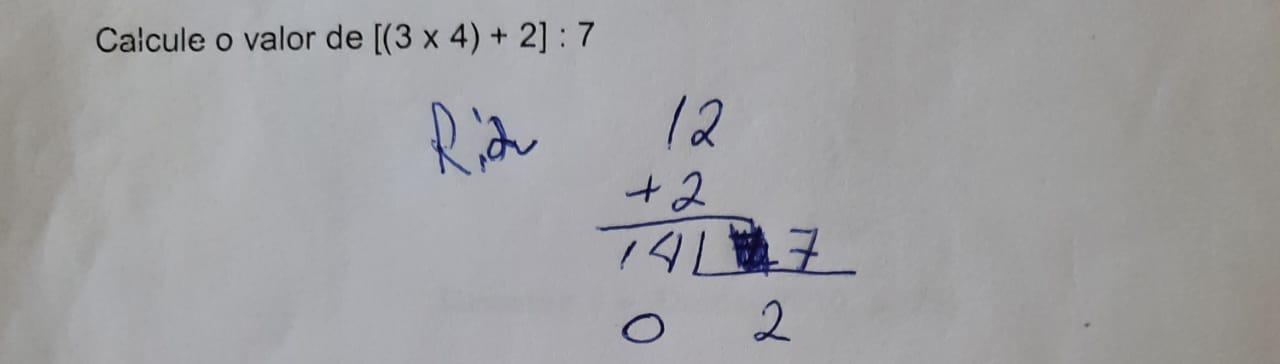
Figura 3: Resolução da dupla A e da dupla C da questão 2 da primeira lista de situações-problema
Fonte: Dante (2010, p. 24).
No decorrer da pesquisa, percebeu-se que a dupla A dialogava a respeito da ordem de como resolver a expressão numérica, conforme as discussões:
Antônio: Essa expressão é fácil.
Artur: Acho que podemos responder direto.
Antônio: Me dá aqui! Vê se pode ser assim.
Artur: Claro! Você fez direto.
Antônio: A gente não precisa obedecer à ordem, dá certo! (Trecho do 1º encontro, em 22 set. 2022).
Percebe-se que, na resolução do problema, as duplas A e C não obedeceram a uma ordem padrão (parênteses, colchetes e chaves). Elas usaram o raciocínio dedutivo, permitindo uma economia de esforço e tempo para encontrar o resultado correto.
Já as duplas B, D, E, F, G, H, I, J, K e o trio L resolveram de forma idêntica, respeitando uma ordem de prevalência e propriedades operatórias, onde também se obteve um resultado satisfatório (Figura 4).
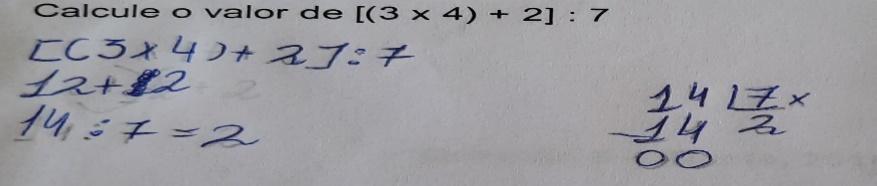
Figura 4: Resolução da dupla B da questão 2 da primeira lista de situações-problema
Fonte: Dante (2010, p. 24).
Destaca-se o passo a passo no qual as expressões numéricas podem ser definidas como o conjunto de operações fundamentais que “são trabalhadas por serem a síntese do estudo das quatro operações básicas; anunciar uma escrita e resolução que envolve regras e passos específicos; comunicação em linguagem matemática” (Ramos et al., 2021, p. 1.296).
Dante (2012, p. 75) afirma que, antes de resolver qualquer expressão numérica, os alunos devem obedecer à hierarquização das operações básicas.
Quando a expressão tem parênteses, resolvem-se primeiro as operações que estão dentro deles. Nas expressões sem parênteses, só com adição ou só com multiplicação, agrupa-se como quiser, pois essas operações possuem a propriedade associativa. Nas demais expressões sem parênteses, efetuam-se as operações nesta sequência: 1º) Potenciação e raiz quadrada, na ordem em que aparecem; 2º) Multiplicação e divisão, na ordem em que aparecem; 3º) Adição e subtração, na ordem em que aparecem.
A partir da definição “resolver situações-problema”, envolvendo os conceitos de “juntar” e “acrescentar”, por meio de registros de representação pessoal, percebe-se que na questão de número 3 foram alcançados seis acertos e 0 erros. A referida questão aborda problemas-padrão simples, com “aplicação direta de um ou mais algoritmos anteriormente aprendidos e não exige nenhuma estratégia” (Dante, 2010, p. 25). A questão tem por objeto matemático adição de números naturais.
Dante (2010, p. 25) explica que nos problemas-padrão
a solução do problema já está contida no próprio enunciado, e a tarefa básica é transformar a linguagem usual em linguagem matemática, identificando as operações ou algoritmos necessários para resolvê-lo. O objetivo desses problemas é recordar e fixar os fatos básicos por meio dos algoritmos das quatro operações fundamentais, além de reforçar o vínculo existente entre essas operações e seu emprego nas situações do dia a dia. De modo geral, eles não aguçam a curiosidade do aluno nem o desafiam.
As duplas A, B, C, D, E, F, G, H, I, J, K e o trio L, solucionaram a questão 3 usando as mesmas estratégias algébricas apresentadas na Figura 5.

Figura 5: Resolução da dupla J da questão 3 da primeira lista de situações-problema
Fonte: Dante (2010, p. 25).
É possível observar que a dupla J aplicou a adição para solucionar o problema. E evidencia-se que houve uma grafia na expressão “há na classe” e reafirmação no comentário para associar o conceito de uso da adição e da multiplicação. O que é relevante porque que ao trabalhar palavras, conceitos envolvidos, aspectos operacionais, interpretativos, ligados com aritmética, principalmente, nas quatro operações da matemática escolar e na interpretação de situações-problema, o estudante é estimulado a transcender os cálculos, desmistificando a Matemática (Andrade; Colares; Costa, 2018).
Na questão 4, foram obtidos sete erros e cinco acertos; trata-se de um problema- padrão composto, que se diferencia do problema-padrão simples por ser solucionado com duas ou mais operações da Matemática escolar (Dante, 2010). Os sete erros foram das duplas B, C, D, E, F, K e do trio L, que solucionaram o problema usando o mesmo raciocínio matemático (Figura 6).

Figura 6: Resolução da dupla D questão 4 da primeira lista de situações-problema.
Fonte: Dante (2010, p. 25).
As duplas e o trio não conseguiram usar mais de uma operação da Matemática escolar para solucionar o problema. Segundo Santomauro (2010 apud Araújo, 2015, p. 301), os estudantes “compreendem o problema, mas apresentam dificuldade em saber qual operação matemática deve ser utilizada para resolvê-lo”.
Expõe-se, a seguir, como a dupla G fez para finalizar a situação-problema, usando a conexão dos algoritmos matemáticos e o desenho “palitinhos” para solucioná-la.

Figura 7: Resolução da dupla G da questão 4 da primeira lista de situações-problema
Fonte: Dante (2010, p. 25).
Pela solução da dupla G, nota-se que a leitura e a interpretação do problema foram feitas de forma satisfatória. Outra observação importante é o significado da palavra “quantidades iguais”. Nesta ocasião, tornou-se evidente que se no enunciado do problema tiver palavras conhecidas, a interpretação do estudante ficará descomplicada, facilitando o desenvolvimento das estratégias para a resolução do problema. Outra situação observada foi o recurso de solução por meio de “palitinhos” que a dupla usou para a divisão. Cavalcanti (2001, p. 127-128) defende que o uso do desenho é um
recurso de interpretação do problema e como registro da estratégia de solução [...]. Algumas crianças iniciam seus registros com desenhos e, posteriormente, passam a empregar números e sinais, em especial nas situações em que têm um domínio maior do tema e dos conteúdos matemáticos envolvidos.
Apresenta-se, a seguir, como a dupla J solucionou a questão 4, da primeira lista de situações-problema (Figura 8). Evidencia-se que a dupla se integrou à situação-problema, identificou os dados envolvidos nela, organizou as ideias por meio dos diálogos e, por último, realizou a verificação do problema.

Figura 8: Resolução da dupla J da questão 4 da primeira lista de situações-problema
Fonte: Dante (2010, p. 25).
O conhecimento matemático é fundamental para que o estudante possa resolver o problema. Logo, uma situação-problema se torna desafiadora, quando propõe ao aluno criar estratégias, objetivando atingir um resultado. Segundo a BNCC (Brasil, 2018, p. 269), no “Ensino Fundamental - anos finais, a expectativa é de que os alunos resolvam problemas envolvendo as operações fundamentais, [...] utilizando estratégias diversas, com compreensão dos processos neles envolvidos”.
Na questão 5, houve acerto da dupla D e 11 erros, das duplas A, B, C, E, F, G, H, I, J, K e do trio L. Nela, são abordados problemas-processo ou heurísticos. Dante (2010, p. 25) os define como
problemas cuja solução envolve operações que não estão contidas explicitamente no enunciado. Em geral, não podem ser traduzidos diretamente para a linguagem matemática, nem resolvidos pela aplicação automática de algoritmos, pois exigem do aluno um tempo para pensar e arquitetar um plano de ação, uma estratégia que poderá levá-lo à solução. Por isso, tornam-se mais interessantes que os problemas-padrão.
Esse tipo de questão incentiva o estudante a encontrar soluções que otimizem o processo de resolução (Dante, 2010), tendo o objeto matemático como princípio fundamental da contagem.
Observa-se, a seguir, a elaboração da solução do problema heurístico realizada pela dupla D para responder à questão (Figura 9).

Figura 9: Resolução da dupla D da questão 5 da primeira lista de situações-problema
Fonte: Dante (2010, p. 26).
Vê-se que o desenho foi a estratégia escolhida pela dupla D para solucionar o problema de forma correta e notável, evidenciando que há diversas maneiras de se chegar à solução, reforçando a crença de que existe uma forma para resolver problemas matemáticos. O desenho
explicita mais facilmente os significados presentes nos textos – palavras, cenas, informações, operações etc. – e assim constroem uma representação mental dos mesmos [...] é importante propor situações nas quais desenhar implique a discussão com parceiros, a troca de ideias, o ato de ouvir e emitir impressões sobre as ideais que o desenho suscitou (Cavalcanti, 2001, p. 128).
Logo, na resolução da situação-problema pela dupla D é perceptível a utilização de diagramas com letras do alfabeto ou iniciais de nomes de pessoas. A análise aborda o erro do problema-processo ou heurístico efetuado pela dupla J (Figura 10).

Figura 10: Resolução da dupla J da questão 5 da primeira lista de situações-problema
Fonte: Dante (2010, p. 26).
Para a maioria dos estudantes seria difícil traduzir para uma expressão matemática esse tipo de problema heurístico (Lester Jr; D’Ambrósio, 1988). Nota-se que a resposta 42 é o resultado de sete vezes seis, como afirmado na questão. Para Lester Jr. e D’Ambrósio (1988, p. 36), os problemas-processo ou heurísticos
são importantes experiências na formação matemática da criança, pois as resoluções envolvem processos mentais [...] para compreensão, planejamento, solução e avaliação da tentativa de solução. São problemas que desenvolvem no aluno a habilidade de decidir como, quando e por que utilizar sua bagagem de conhecimentos matemáticos.
Na questão 6 (Figura 11) foi alcançado 0 acertos e 12 erros. São abordados, na situação-problema, os problemas de quebra-cabeça, pois Dante (2010, p. 25, grifo do autor) afirma que “problemas envolvem e desafiam os alunos [...] constituem a chamada Matemática recreativa, e sua solução depende de um golpe de sorte ou da facilidade em perceber algum truque [...] que é a chave da solução”.

Figura 11: Questão 6 da primeira lista de situações-problema
Fonte: Dante (2010, p. 28).
Portanto, problemas desse tipo, com a solução não destacada no enunciado e que não pode ser resolvido por meio de algoritmos automáticos, precisará de mais tempo de reflexão do aluno a fim de que estabeleça um plano de ação, buscando uma estratégia criativa que o leve à solução.
Realizou-se a socialização, que teve por finalidade oferecer aos sujeitos da pesquisa a possibilidade de refletirem, compreenderem e explicitarem as maneiras utilizadas durante a resolução das situações-problema, discutindo as estratégias elaboradas por eles e pelos colegas.
No momento da socialização, os alunos tiveram a oportunidade de ir ao quadro para resolver questões que compunham a lista de situações-problema. Diante do cenário retratado, observou-se que as duplas e o trio resolveram de forma correta as questões de nº 1, 2 e 3. Enfatiza-se que essas questões tiveram 100% de acertos (Gráfico 1).
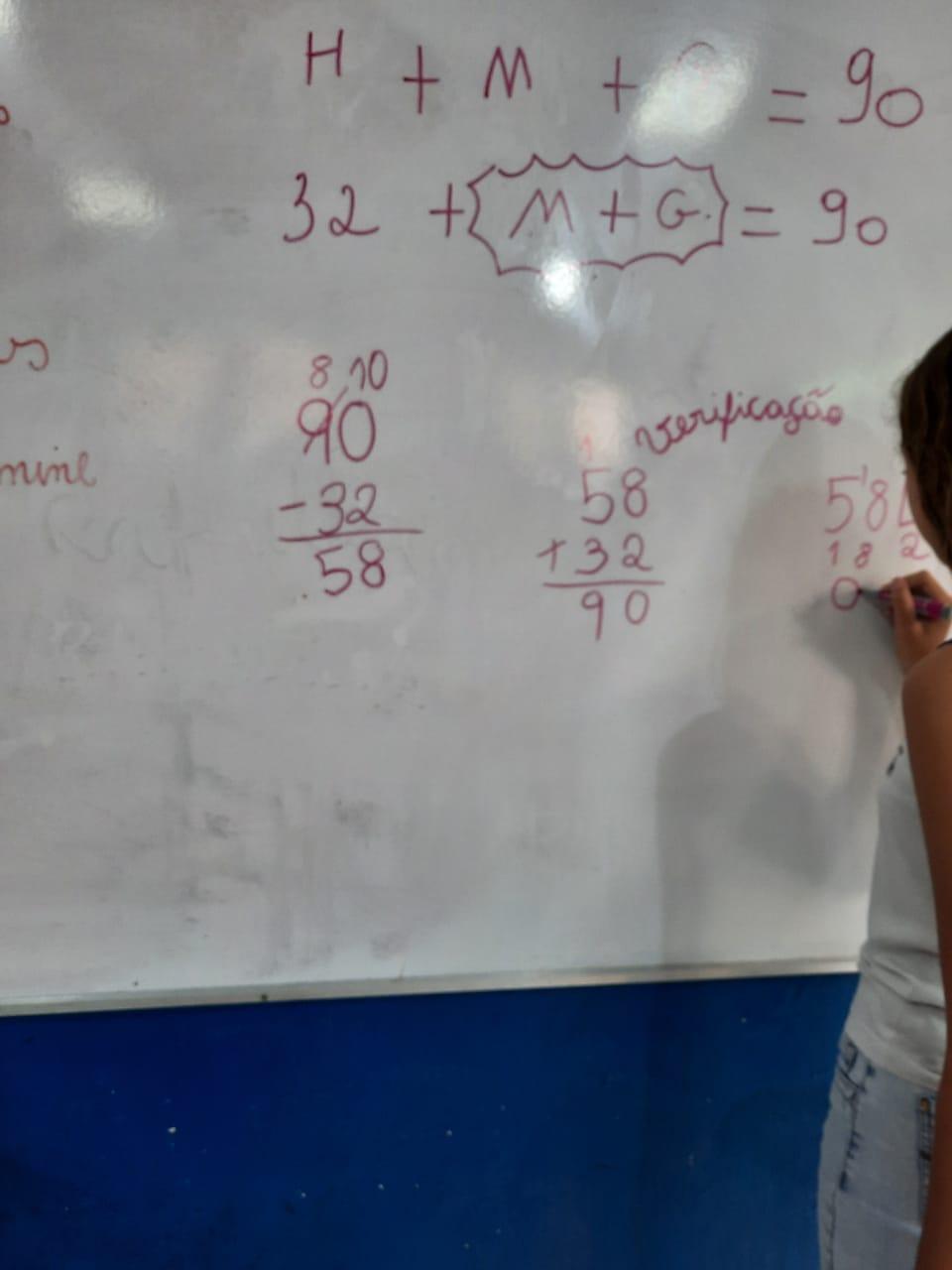
Figura 12: Momento da socialização dos sujeitos da pesquisa
No decorrer da socialização, percebemos algumas duplas praticando equívocos na resolução das questões 4, 5 e 6, contudo erros não devem ser vistos de maneira negativa, mas como possibilidades de os alunos verem o que está incorreto. Como afirma Lorenzato (2008, p. 50),
ao professor compete, primeiramente, dispensar constante atenção para constatar o erro, lembrando que acerto pode camuflar erro. É importante diagnosticar como o erro se deu, sem o que será impossível encontrar a(s) causa(s) dele. Nessa fase, é fundamental ouvir o aluno, conversar com ele com o objetivo de desvelar seu pensamento e seus motivos. Feita a diagnose, convém propor ao aluno uma ou mais situações com as quais ele possa perceber a incoerência de suas respostas ou posições. Auxiliando o aluno a descobrir novas alternativas, podemos esperar que ele reformule seus conceitos, corrija o erro e, assim, evolua.
Destarte, é importante que os professores reflitam a respeito dos problemas ou das dificuldades encontradas por seus alunos e sejam positivos a respeito do termo “erro”, entendendo quais são as demandas desses estudantes. Portanto, situações como essas são relevantes para o ensino-aprendizagem dos conceitos da Matemática escolar.
Considerações finais
As estratégias diversificadas ou similares, adotadas na resolução de problemas pelos alunos sujeitos da pesquisa, incluíram: raciocínio lógico, contagem de palitinhos e diálogos para executar um plano de verificação, identificação e aplicação das operações matemáticas. Entretanto, a interpretação do problema é fundamental para a escolha das estratégias na resolução do problema. Cada aluno identifica e resolve a questão em consonância com o seu conhecimento matemático, a sua capacidade interpretativa e a estratégia que julgar mais adequada.
A socialização representa o diferencial da pesquisa quanto à proposição de buscar estratégias como as preconizadas por Pólya, que incluem: compreender, elaborar um plano, executar o plano e fazer um retrospecto. As referidas etapas foram demonstradas sem mencionar o conceito específico de cada uma delas, para que a abordagem seja prática e os erros não sejam explorados com um caráter de reprovação, mas como oportunos às etapas apresentadas, caminhos para o alcance de estratégias e respostas corretas.
Referências
ANDRADE, W. M.; COLARES, G. S.; COSTA, M. R. Uma análise sobre as dificuldades dos alunos nas operações fundamentais. In: CONGRESSO NACIONAL DE EDUCAÇÃO, 5., 2018, Olinda. Anais… Campina Grande: Realize, 2018. Disponível em: https://editorarealize.com.br/artigo/visualizar/49210.pdf. Acesso em: 23 jan. 2023.
ARAUJO, N. K. S. Análise das dificuldades na resolução de problemas matemáticos por alunos do 5º ano do Ensino Fundamental. 2015. 139f. Dissertação (Mestrado em Ensino de Ciências Naturais e Matemática) – Universidade Federal de Sergipe, São Cristóvão, 2015. Disponível em: https://ri.ufs.br/bitstream/riufs/5174/1/NATALIA_KELI_SANTOS_ARAUJO.pdf. Acesso em: 12 mar. 2023.
BRANCA, N. Resolução de problemas como meta, processo e habilidades básicas. In: KRULIK, S.; REYS, R. (org.). A resolução de problemas na Matemática escolar. São Paulo: Atual, 1997. p. 4-12.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 5 jul. 2022.
BRITO, M. R. F. de. Alguns aspectos teóricos e conceituais da solução de problemas matemáticos. In: BRITO, M. R. F. (org.). Solução de problemas e a matemática escolar. Campinas: Alínea, 2006.
CAVALCANTI, C. T. Diferentes formas de resolver problemas. In: SMOLE, K. S.; DINIZ, M. I. (org.). Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática. Porto Alegre: Artmed, 2001. p. 121-149.
D’AMBRÓSIO, U. Por que e como ensinar história da Matemática. Rematec, Belém, v. 8, n° 12, p. 7-21, 2013. Disponível em: http://www.rematec.net.br/index.php/rematec/article/view/355/355. Acesso em: 22 dez. 2022.
DANTE, L. R. Didática da resolução de problemas de Matemática. 2ª ed. São Paulo: Ática, 1991.
DANTE, L. R. Didática da resolução de problemas de Matemática. São Paulo: Ática, 1995.
DANTE, L. R. Formulação e resolução de problemas de Matemática: teoria e prática nas aulas de Matemática. São Paulo: Ática, 2010.
DANTE, L. R. Projeto Telares: Matemática (Ensino Fundamental) - 6º ano. São Paulo: Ática, 2012.
GAZZONI, A.; OST, A. A resolução de um problema: soluções alternativas e variações na formulação. Vidya, Santa Maria, v. 28, n° 2, p. 37-45, jul./dez. 2008. Disponível em: https://periodicos.ufn.edu.br/index.php/VIDYA/article/view/341. Acesso em: 5 mar. 2023.
GOULART, C. M. A.; AGUIAR, M. A. L. de. Relatos de sala de aula: análise em busca de compreensão da perspectiva discursiva de alfabetização. Pensares em Revista, São Gonçalo, n° 14, jan./abr. 2019. Disponível em: https://www.e-publicacoes.uerj.br/pensaresemrevista/article/view/35932. Acesso em: 29 maio 2023.
GUIMARÃES, H. M. Jeremy Kilpatrick: entrevista a George Pólya. Quadrante, Lisboa, v. 19, n° 2, p. 103-119, 2010. DOI: https://doi.org/10.48489/quadrante.22850. Disponível em: https://quadrante.apm.pt/article/view/22850. Acesso em: 5 mar. 2023.
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA (IBGE). Censo Brasileiro de 2022. Rio de Janeiro: IBGE, 2022. Disponível em: https://www.ibge.gov.br/cidades-e-estados/es/muqui.html. Acesso em: 22 abr. 2022.
LESTER Jr., F. K.; D'AMBROSIO, B. S. Tipos de problemas para a instrução matemática no primeiro grau. Bolema, Rio Claro, v. 3, n° 4, 1988. Disponível em: https://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/
10747. Acesso em: 12 mar. 2023.
LORENZATO, S. Para aprender Matemática. 2ª ed. Campinas: Autores Associados, 2008.
MARTINS, W. da S. A resolução de problemas de Geometria Espacial sob a perspectiva dos conceitos vygotskyanos. 2019. 176f. Dissertação (Mestrado em Ensino de Ciências) – Universidade Cruzeiro do Sul, São Paulo, 2019. Disponível em: https://repositorio.up.edu.br/jspui/handle/123456789/364. Acesso em: 2 mar. 2023.
MATEUS, A. A. et al. Problemas matemáticos: caracterização, importância e estratégias de resolução. São Paulo: Instituto de Matemática e Estatística da Universidade de São Paulo, 2001. Trabalho acadêmico. Disponível em: https://www.esev.ipv.pt/mat1ciclo/Resolucao%20probs/mat450-2001242-seminario-8-resolucao_problemas.pdf. Acesso em: 8 dez. 2022.
PÓLYA, G. A arte de resolver problemas. Rio de Janeiro: Interciência, 2006.
POZO, J. I.; ANGÓN, Y. P. A solução de problemas como conteúdo procedimental da Educação Básica. In: POZO, J. I. (org.). A solução de problemas: aprender a resolver, resolver para aprender. Trad. Beatriz Affonso Neves. Porto Alegre: Artmed, 1998. p.139-175.
RAMOS, R. de C. de S. S. et al. Situações de expressões numéricas em livros didáticos de 6° ano: uma análise segundo a Teoria dos Campos Conceituais. Bolema, Rio Claro, v. 35, n° 71, p. 1.294-1.315, dez. 2021. DOI: https://doi.org/10.1590/1980-4415v35n71a04. Disponível em: https://www.scielo.br/j/bolema/a/XrDSvx4WmjCvLNbgcdwLCNv/. Acesso em: 12 ago. 2022.
SOARES, I. S.; OLIVEIRA, J. S. de. Leitura, compreensão e interpretação de enunciados matemáticos: conceito de divisibilidade, dificuldades, desafios e perspectivas. In: CONGRESSO NACIONAL DE PESQUISA E ENSINO DE CIÊNCIAS, 1., 2016, Campina Grande. Anais... Campina Grande: Realize, 2016. Disponível em: https://www.editorarealize.com.br/artigo/visualizar/18068. Acesso em: 19 dez. 2022.
SOUTO, F. C. F.; GUÉRIOS, E. C. O ensino de Matemática e a resolução de problemas contextualizados nos anos iniciais do Ensino Fundamental. In: ENCONTRO PARANAENSE DE EDUCAÇÃO MATEMÁTICA, 14., 2017, Cascavel. Anais... Londrina: Sociedade Brasileira de Educação Matemática, 2017. Disponível em: http://www.sbemparana.com.br/eventos/index.php/EPREM/XIV_EPREM/paper/
viewFile/280/182. Acesso em: 23 jan. 2023.
VALLILO, S. A. M. O estudo da linguagem matemática na sala de aula: uma abordagem através da resolução de problemas. In: ENCONTRO BRASILEIRO DE ESTUDANTES DE PÓS-GRADUAÇÃO EM EDUCAÇÃO MATEMÁTICA, 20., 2016, Curitiba. Anais... Curitiba, 2016. Disponível em: http://www.ebrapem
2016.ufpr.br/wp-content/uploads/2016/04/gd14_sabrina_vallilo.pdf. Acesso em: 13 fev. 2023.
Publicado em 12 de novembro de 2024
Como citar este artigo (ABNT)
AMARAL, André Silveira do; GUALANDI, Jorge Henrique; ABREU, Vanessa Holanda Righetti de. Resolução de problemas nos processos de ensino de Matemática na Educação Básica: uma proposta com alunos do 6º ano do Ensino Fundamental. Revista Educação Pública, Rio de Janeiro, v. 24, nº 42, 12 de novembro de 2024. Disponível em: https://educacaopublica.cecierj.edu.br/artigos/24/42/resolucao-de-problemas-nos-processos-de-ensino-de-matematica-na-educacao-basica-uma-proposta-com-alunos-do-6-ano-do-ensino-fundamental
Novidades por e-mail
Para receber nossas atualizações semanais, basta você se inscrever em nosso mailing
Este artigo ainda não recebeu nenhum comentário
Deixe seu comentárioEste artigo e os seus comentários não refletem necessariamente a opinião da revista Educação Pública ou da Fundação Cecierj.

